铰链点可互换的近似直线机构综合方法及解域研究

尹来容 黄 娟 胡 林 刘 鑫 张志勇

1.长沙理工大学,长沙,4101142.湖南省工程车辆轻量化与可靠性技术重点实验室,长沙,4101143.湖南农业大学东方科技学院,长沙,410012

铰链点可互换的近似直线机构综合方法及解域研究

尹来容1,2黄 娟3胡 林1刘 鑫1张志勇1

1.长沙理工大学,长沙,4101142.湖南省工程车辆轻量化与可靠性技术重点实验室,长沙,4101143.湖南农业大学东方科技学院,长沙,410012

基于拐点圆极点理论，给出了一种可以综合出无穷多铰链四杆近似直线机构的方法。用解析法证明了该方法综合出近似直线机构的一个连架杆的固定铰链点和对应动铰链点可以互换，铰链点互换前后得到的两个机构具有相同的鲍尔点和直线方向，另外一个连架杆不变。推导了综合曲柄摇杆直线机构的公式，并绘制了曲柄摇杆机构解域图。计算示例表明该方法简单有效，能迅速综合出曲柄摇杆直线机构，且综合出的机构动铰链点和固定铰链点可互换。所得到的近似直线机构为实际工程应用提供了更多选择。

直线机构；拐点圆；圆点曲线；机构综合

0 引言

直线机构从18世纪瓦特时代就开始得到应用，铰链四杆近似直线导引机构综合问题属于机构学中的一个经典问题[1-4]，并得到了广泛应用[5-6]。文献[7]对瞬心无穷远的直线机构进行了研究。文献[8]用解析法综合出了“λ型”四杆直线机构。文献[9-11]利用鲍尔点理论，综合出了无穷多直线机构解，并采用机构解域[12]的方法，对无穷多机构解进行了优选。文献[13-15]结合四位置运动生成和刚体导引机构综合问题，进一步拓展了解域理论。以上研究在一定程度上推动了经典近似直线机构综合理论与机构解域理论的融合，但是，对于曲率驻点曲线退化情况下的近似直线机构综合与解域一体化研究问题，涉及较少。

本文给出了一种特殊情况下的近似直线机构综合方法，且综合出的无穷多机构的一个连架杆的固定铰链点和动铰链点可以互换。

1 铰链点互换证明

拐点圆上的点的曲率半径为无穷大，除了瞬心点之外的任意点的运动轨迹均有一段近似直线，且拐点圆极点的直线段最长。曲率驻点曲线为动平面上轨迹曲率为驻点的点的集合，一般情况下为一三阶曲线，当机构处于特殊型位时，将分解为圆和直线或三条直线。鲍尔点是拐点圆和曲率驻点曲线的交点，利用鲍尔点可以综合出近似直线机构。当拐点圆极点和鲍尔点重合时，可以得到直线长度更长、精度更高的直线机构。

当瞬心点P与固定铰链点A0重合，固定铰链点A0和B0、动铰链点B共线时，曲率驻点曲线退化成两条直线，拐点圆极点和鲍尔点重合，另外一个动铰链点A可以在机架的垂直方向上任意选取[7]。下面证明此种特殊情况下，固定铰链点A0和动铰链点A可以互换，且互换后的机构具有同一个鲍尔点P1和直线方向β1，另外一对动铰链点B和定铰链点B0不变，如图1所示(图1b中，P1点位于连杆AB的延长线上，且此时连杆AB与连架杆B0B共线)。

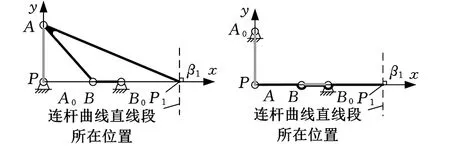
(a)互换前 (b)互换后

曲率驻点曲线可由Euler-Savary方程[7,11]求导后得到，方程为

(1)

式中,r为曲率驻点在极坐标系(P,r,α)中的极径，起始点为瞬心P；D为拐点圆直径;M，N为辅助变量；其他参数的定义可参考文献[7]。

当1/N→0且1/M→0时，拐点圆直径为极大值，即

D=lP1P

(2)

由曲率驻点曲线方程可知，曲率驻点曲线退化为

sin α=0 cos α=0 1/r=0

(3)曲率驻点曲线退化为与坐标轴重合的两条直线，以及一条无穷远直线，且动铰链点A可以在y轴上任意选取。由于已知瞬时极点P与铰链点A0(A)重合，动铰链点B和固定铰链点B0也已给定，因此，可以根据Euler-Savary方程得到拐点圆极点JB：

(4)

拐点圆极点JB与鲍尔点P1重合。由于动铰链点A可在y轴上任意选取，固定铰链点A0与动铰链点A互换前后，瞬心P点位置不变，所以由式(4)可求出相同的鲍尔点P1。

2 曲柄摇杆机构综合公式推导

下面以图1b铰链点互换后机构为例，推导曲柄摇杆机构综合公式。以动铰链点A为坐标原点，固定铰链点A0=(0,y)，鲍尔点P1=(x,0)，在机构运动平面内直接建立直角坐标系，横纵坐标上的点两两组合对应一个机构，即为一个机构解，全部机构解的集合构成机构解域。为了便于分析和简化计算，不妨令lAB0(lA0B0)=1(在实际应用当中只需乘以实际AB0(A0B0)的长度)。考虑到对称性，只需讨论y>0上半平面。由解析法可得动铰链点B的坐标[11]：

(5)

根据给定的机架A0B0、动铰点A以及求出的动铰点B的坐标，四杆机构各杆长为

(6)

其中，鲍尔点P1取x>0时，

鲍尔点P1取-1

鲍尔点P1取x<-1时，

根据曲柄摇杆机构的格拉霍夫定理：最短杆杆长与最长杆杆长之和需小于其他两杆杆长之和，且最短杆为连架杆或机架。由图1三角形边长关系知，最长杆必为机架A0B0。当连架杆A0A为曲柄时，a+d

(7)

将式(6)代入式(7)，得

(8)

整理可得

(9)

对于任意给定的固定铰链点A0=(0,y)和鲍尔点P1=(x,0)值，满足式(9)即可得到曲柄摇杆机构。若不满足式(9)，对于综合出的无穷多机构解，还可以根据不同的设计要求，如杆长比、最小传动角等，采用机构解域的方法快速直观地优选出最优机构解，具体方法见文献[12]。

3 计算示例

直线机构在包装机械、农业机械以及工程车辆等领域有着广泛的应用。文献[16]采用曲柄摇杆近似直线机构，设计了某企业自动流水线的升降式送料装置。在实际工程应用中，设计者需要根据用户客观的加工条件和装配空间等设计出性价比高的机构，因此，除了设计时需对综合出的机构施加各种结构和性能约束外，还需要考虑机构的实际安装位置与运动空间范围。

以动铰链点A为坐标原点，固定铰链点A0=(0,y)，鲍尔点P1=(x,0)，取机架长度lA0B0=100，令-360

图2 曲柄摇杆机构类型分布解域图

4 结论

(1)给出了一种综合铰链点可互换的近似直线机构的方法，并用解析法证明了该方法的正确性。

(a)机构M1 (b)机构M2

(a)铰链点互换前Ma (b) 铰链点互换后Mb

表1 机构结构和性能参数

(2)铰链点互换前后得到的两个机构具有相同的鲍尔点和直线方向，且其中一个连架杆不变。

(3)推导了综合曲柄摇杆近似直线机构的公式，并绘制了曲柄摇杆机构解域图。

(4)计算示例表明该方法简单有效，能迅速综合出曲柄摇杆近似直线机构，且综合出的机构的动铰链点和固定铰链点可互换，解决了实际应用中可能存在的固定铰链点位置与已有设备位置冲突的问题，为实际工程应用提供了更多选择。

[1] Norton R L. Design of Machinery[M]. 3rd ed. New York :McGraw-Hill Inc., 2004.

[2] Mc Carthy J M, Soh G S. Geometric Design of Linkages[M]. 2nd ed. New York: Springer-Verlag, 2010.

[3] Hunt K H. Kinematic Geometry of Mechanisms[M]. London: Oxford University Press, 1978.

[4] Dijksman E A. Motion Geometry of Mechanisms[M]. Cambridge :Cambridge University Press, 1976.

[5] 蔡高参，王忠. Tchebycheff Lambada直线机构与4足机器人运动特性研究[J]. 机械设计，2010，27(5)：35-38. Cai Gaocan, Wang Zhong. Research on the Kinetic Characteristic of Tchebycheff Lambada Straight Line Mechanism and Four Legged Robot[J]. Journal of Mechanical Design，2010，27(5)：35-38.

[6] 钱卫香，韩建友. 液压支架含拐点直线导路机构综合与分析[J]. 北京科技大学学报，2013,35(2)：234-241. Qian Weixiang, Han Jianyou. Synthesis and Analysis of Straight Line Guiding Mechanisms in Hydraulic Supports Using Inflection Points[J]. Journal of University of Science and Technology Beijing，2013,35(2)：234-241.

[7] 王忠, 朱洪俊, 廖磊,等. 瞬心无穷远时近似直线轨迹的四杆机构综合[J]. 机械工程学报，2007，43(10)：46-49. Wang Zhong, Zhu Hongjun, Liao Lei, et al. Synthesis of Four-bar Appropriate Straight Line Linkage with Infinitely Far Instant Center[J]. Chinese Journal of Mechanical Engineering，2007，43(10)：46-49.

[8] Han Jianyou, Qian Weixiang, Zhao Huishe. Study on Synthesis Method of λ-formed 4-bar Linkages Approximating a Straight Line[J]. Mechanism and Machine Theory, 2009，44(1)：57-65.

[9] Yin Lairong, Han Jianyou, Mao Cong. SynthesisMethod Based on Solution Regions for Planar Four-bar Straight-line Linkages[J]. Journal of Mechanical Science and Technology,2012,26(10)：3159-3167.

[10] 尹来容，韩建友. 基于解域分析的直线机构综合方法研究[J]. 北京科技大学学报，2011，33 ( 2 )：237-243. Yin Lairong, Han Jianyou. Synthesis Research of Straight-line Mechanisms by Analyzing Solution Regions[J]. Journal of University of Science and Technology Beijing, 2011，33 ( 2 )：237-243.

[11] 钱卫香. 实现三阶密切直线导路机构解析全解[J]. 机械设计与研究，2013,29(2)：11-14. Qian Weixiang. Comprehensive Analytical Solution for Linkages Approximating a 3-order Osculating Straight Line[J]. Journal of Machine Design and Research，2013,29(2)：11-14.

[12] Han Jianyou, Qian Weixiang. On the Solution of Region-based Planar Four-bar Motion Generation[J]. Mechanism and Machine Theory, 2009, 44(2): 457-465.

[13] 韩建友，崔光珍，杨通. 六杆机构四位置运动生成的解域综合理论与方法[J]. 北京航空航天大学学报, 2014,40(9): 1170-1175. Han Jianyou, Cui Guangzhen, Yang Tong. Solution Region Synthesis Theory and Method of Six-bar Linkages with 4-position Motion Generation[J]. Journal of Beijing University of Aeronautics and Astronautics,2014,40(9): 1170-1175.

[14] 韩建友，李人武，杨通,等. Watt-I型六杆刚体导引机构的解域综合方法[J]. 工程科学学报，2015，37(5)：655-660. Han Jianyou, Li Renwu, Yang Tong, et al. Solution-region Synthesis Approach of a Watt-I Six-bar Rigid-body Guidance Mechanism[J]. Chinese Journal of Engineering，2015，37(5)：655-660.

[15] Yang Tong, Han Jianyou, Yin Lairong. A Unified Synthesis Method Based on Solution Regions for Four-position Finitely Separated and Mixed “Point-Order” Positions[J]. Mechanism and Machine Theory, 2011, 46: 1719-1731.

[16] 尹来容, 韩建友. 特殊情况下的直线机构解域分析及综合方法[J]. 农业机械学报，2011，42(4)：190-194. Yin Lairong, Han Jianyou.Solution-region Analysis and Synthesis Method of Straight-line Mechanism in the Special Configuration[J]. Transactions of the Chinese Society for Agricultural Machinery，2011，42(4)：190-194.

(编辑 王旻玥)

Study on Synthesis Method and Solution-region of Approximate Straight-line Linkage with Two Inter-convertible Pivots

Yin Lairong1,2Huang Juan3Hu Lin1Liu Xin1Zhang Zhiyong1

1. Changsha University of Science and Technology, Changsha, 4101142.Hunan Key Laboratory of Lightweight and Reliability Technology for Engineering Vehicle, Changsha, 4101143.Orient Science and Technology College, Hunan Agriculture University, Changsha, 410012

A synthesis method of four-bar approximate straight-line mechanism was presented based on inflection circle pole theorem, which might produce an infinite number of mechanisms. An analytic method was introduced to prove that the synthesized mechanism might make the fixed pivot of side link and its corresponding moving pivot inter-convertible. The two synthesized linkages with two inter-convertible pivots contained the same Ball point and straight-line direction. The other side link remained unchanged. The synthesizing formulas of crank-rock mechanism were derived and the solution domains were plotted. The given examples show that the method is simple and efficient to synthesize crank-rock mechanism, and the synthesized mechanisms have two inter-convertible pivots. This approximate straight-line linkage may provide more choices for practical engineering applications.

straight-line linkage; inflection circle; circle point curve; mechanism synthesis

2016-01-29

国家自然科学基金资助项目(51305047)；湖南省科技计划资助重点项目(2015GK3020)；湖南省重点实验室开放基金资助项目(KF1505)

TH112.1

10.3969/j.issn.1004-132X.2016.24.015

尹来容，男，1984年生。长沙理工大学汽车与机械工程学院讲师、博士。主要研究方向为机械设计理论、机构综合与CAD。出版专著1部，发表论文10余篇。黄 娟，女，1983年生。湖南农业大学东方科技学院讲师。胡 林，男，1978年生。长沙理工大学汽车与机械工程学院副教授。刘 鑫，男，1981年生。长沙理工大学汽车与机械工程学院副教授。张志勇，男，1976年生。长沙理工大学汽车与机械工程学院副教授。