基于虚拟光笔的坐标测量系统探针结构的设计

张 瑞 刘书桂 张 新 王有富

1.天津大学精密测试技术与仪器国家重点实验室，天津，3000722.九江精密测试技术研究所，九江，332000

基于虚拟光笔的坐标测量系统探针结构的设计

张 瑞1刘书桂1张 新2王有富2

1.天津大学精密测试技术与仪器国家重点实验室，天津，3000722.九江精密测试技术研究所，九江，332000

针对光笔式测量系统模型的特征，基于虚拟光笔，建立了一种新的光笔结构。系统中采用的光笔共有10个控制点，设光笔前面6个控制点所在的平面与后面4个控制点所在的平面之间的距离为DFB。利用三坐标测量机主轴运动的高精度、高稳定性，构造了不同DFB的虚拟光笔。详细说明了虚拟光笔的构造模型，并通过实验证明了DFB参数对系统测量稳定性有着显著的影响，且DFB的最优值为80 mm，通过精度对比实验进一步证明了该结论。

光笔式坐标测量系统；探针结构；测量精度；虚拟光笔

0 引言

传统的三坐标测量技术存在测量系统体积庞大、对测量环境要求较高等劣势，难以满足现代工业的在线测量要求，针对此问题研究者们提出了多种新型便携式坐标测量技术。其中，融合了机器视觉技术的光笔式坐标测量系统以其便携、使用灵活、精度高、测量范围广、能测量隐藏点等优点，受到了业内的广泛关注[1-4]。

作为光笔式坐标测量系统中直接接触被测工件的手持式探针-光笔的结构参数，对整个系统的测量精度和稳定性有着重要的影响。虽然关于光笔式坐标测量系统，国内外均开展了大量的研究工作,但对于光笔结构的设计即光笔控制点的空间分布这一研究领域，目前搜索到的文献中很少有对其进行深入、详细的分析。对于光笔的结构，通常只是要求其设计美观、利于长时间手持。而对于其上分布的控制点，在其个数满足系统唯一解的前提下，数量尽可能多且均匀地分布在较大的三维空间中，也就是在满足其他条件的情况下，尽可能增大光笔的尺寸[1，5-6]。本文针对光笔的结构参数对系统精度和稳定性的影响问题，即光笔控制点的空间分布对系统测量精度和稳定性的影响问题进行了深入的研究。

1 光笔式坐标测量系统

1.1 系统构成及测量原理

光笔式坐标测量系统的构成如图1所示，由一支光笔，一台或两台相机，一台装有配套软件的笔记本电脑及其他附件组成。光笔上按照一定规律分布着若干个控制点(主动发光或被动发光的光源，本系统采用LED作为控制点)，且安装有一个可更换的探头。本系统中采用的光笔结构如图2所示。光笔上共有10个直径均为10 mm的LED，可发出亮度均匀的波长为550 nm的面光源。LED的标号显示在图2中，其中标号1～4的LED均在平面B上，且共线。而标号5～7、标号8～10的LED均在平面F上，同样也分别共线。这三条直线互相平行，平面B与平面F相距16 mm。

图1 系统构成

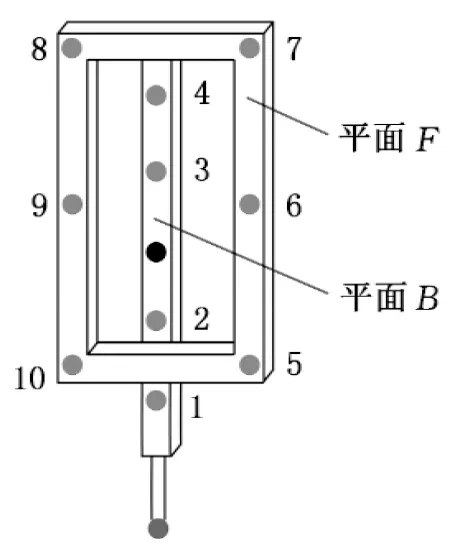
图2 光笔结构图

当光笔探头稳定接触待测工件后，相机采集光笔上LED的图像，经过若干复杂的图像处理算法后得到探头中心在相机坐标系中的三维坐标。再通过包络面等算法可以得到待测工件上与光笔探头接触的待测点在相机坐标系中的坐标值。当获得若干个工件表面待测点的坐标后，即可间接得到需要的几何量参数，如长度、平面度、表面粗糙度等。 正因为光笔式系统在进行测量时，相机只需采集到稳定的光笔上LED图像即可，而无需采集光笔探头的图像，因此使用本系统测量深孔等隐藏点时，虽然光笔探头因进入到深孔中而被遮挡，无法成像，但只要光笔上的LED能够稳定成像，仍然能够实现待测点的在线测量。而这也是光笔式测量系统相对于其他测量系统的最大优势。

1.2 系统模型中坐标系的建立

本系统的数学模型为基于旋转平移矩阵的P10P问题(perspective 10 points problem)，系统模型中共有如图3所示的四种坐标系：

(1)光笔坐标系OLUVW。坐标系原点OL为图2中标号1的LED中心在平面F上的投影。U轴设计为平行于标号10与5的LED中心的连线，正方向从标号10指向标号5。V轴设计为平行于标号1与4的LED中心的连线，正方向从标号1指向标号4。而W轴可根据右手定则确定。

(2)像素坐标系O1x1y1。原点O1设在成像平面的右上角，而x1轴与y1轴分别平行于像素阵列的水平方向和竖直方向。x1与y1正方向的建立原则是使得像素坐标系中每个像素的坐标值均为正数。

(3)像平面坐标系O2x2y2。像平面坐标系的原点O2为相机光轴与像平面的交点，而x2轴与y2轴分别平行于x1轴与y1轴，且方向也与之相同。

(4)相机坐标系OCXYZ。原点OC为相机的透视中心，而X轴与Y轴分别平行于x1轴与y1轴，并且方向也与之相同。即x1轴和y1轴、x2轴和y2轴与X轴和Y轴的对应坐标轴互相平行，且方向相同。而相机坐标系的Z轴可根据右手定则确定，为相机的光轴，正方向为由OC指向O2。

图3 系统模型坐标系的建立

1.3 系统模型

由1.1节中光笔式坐标测量系统的测量原理可知，若要得到被测几何量参数，关键是如何精确地获得探头中心在相机坐标系中的坐标值。当光笔探头稳定接触工件表面的待测点后，调整光笔姿态，使得其上的10个LED尽可能正对相机，且处于相机的视场中间位置。相机采集光笔上LED的图像，通过图像预处理、二值化、边缘检测及轮廓跟踪、中心点定位等算法，获得10个LED所成像的中心在O1x1y1中的坐标(x1i,y1i)(i=1, 2，…，10)。因此有

(1)

其中，(x2i,y2i) (i=1, 2，…，10)为LED所成像的中心在O2x2y2坐标系中的坐标，而(δx,δy, dx, dy, cx, cy)是相机的内部参数，可通过相机标定[7]获得：

(2)

式中，f为相机的焦距，也是相机的内部参数之一；(xi, yi, zi)(i=1, 2，…，10)为LED所成像的中心在OCXYZ中的坐标。

由式(1)、式(2)可以计算出10个LED所成像的中心在相机坐标系OCXYZ中的三维坐标值：

(3)

(4)

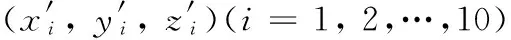
10个LED中心在光笔坐标系OLUVW的三维坐标(ui, vi, wi)(i=1,2，…，10)可以预先通过CMM、影像仪等精确测得，所以由式(3)与式(4)，通过非线性方程组最小二乘解的广义逆算法[8]，可以获得光笔坐标系与相机坐标系之间的旋转矩阵R及平移矩阵T。

如果光笔球形探头中心在OLUVW坐标系中的坐标 (u0, v0, w0)已预先标定，则探头中心在相机坐标系中的三维坐标(x0, y0, z0)可以通过下式得到：

(5)

当获得若干个与待测工件表面稳定接触的探头中心的三维坐标后，再通过特定的算法处理，即可实现被测几何量的测量[9]。

2 虚拟光笔构造模型

光笔的结构参数对系统测量精度和稳定性的影响问题，也就是光笔控制点的空间分布对系统测量精度和稳定性的影响问题，其本质是求光笔控制点在光笔坐标系中的坐标值(ui,vi,wi)(i=1，2，…，n，n≥6)对式(4)求解精度的影响。当空间控制点个数大于等于6时，1.3节中的系统模型有唯一解。本文对系统中采用的光笔结构进行了深入分析，重点研究了图2光笔结构图中平面B与平面F之间的距离参数DFB对系统测量稳定性的影响。而为了研究此距离参数对系统测量稳定性的影响，则需要使用多个不同DFB参数的光笔用于实验，但这样花费的成本将会很高。因为CMM能够实现高精度的测量，为了保证测量精度及稳定性，CMM的主轴在精密驱动结构及误差补偿机制下，需要保证高精度、高稳定性的运动。而本文利用CMM主轴运动的高精度、高稳定性，构造了不同DFB距离参数的虚拟光笔。

图4 虚拟光笔构造

图5 虚拟光笔构造示意图

如图4所示，将光笔稳定地束缚在CMM竖直方向的主轴(Z轴)上，调整光笔的位置，使得CMM的Y轴(垂直于纸面方向)运动方向尽量垂直于光笔的F面与B面。调整相机的位置，使得CMM的Y轴尽量与相机光轴方向平行。如图5所示，每次控制CMM的主轴在Y轴方向运动16 mm(光笔的初始DFB为16 mm)，共运动29次，即光笔在CMM的Y轴方向共运动464 mm，每个位置均采集50幅图像。对30个位置共1500幅的光笔LED图像进行处理，获得每幅图像中每个LED所成像中心在相机坐标系OCXYZ中的坐标。取位置1上标号1～10的LED所成像参与算法运算时，光笔的DFB就是初始的16 mm；取位置1上标号5～10的LED所成像和位置2上标号1～4的LED所成像组合参与算法运算时，光笔的DFB为32 mm，等效为两平面距离DFB为32 mm的光笔参与成像；以此类推，取位置1上标号5～10的LED所成像和后续位置上标号1～4的LED所成像组合参与运算时，等效为两平面距离DFB为16n mm(n=1，2，…，30)的光笔参与成像。构造的虚拟光笔三维结构图见图6。

图6 虚拟光笔三维结构图

3 实验及结果分析

3.1 虚拟光笔稳定性实验及结果分析

按照上述模型构造DFB=16n mm(n=1，2，…，30)的虚拟光笔。为了最大程度地减小随机误差的影响，使用尽可能多的图像进行处理，从而保证结果的可靠性。如图7所示，每个位置的光笔均采集50幅图像，位置1的第m(m=1，2，…，50)幅图像中标号5～10的LED所成像分别与位置n (n=1，2，…，30)的每一幅图像中标号1～4的LED所成像进行组合以构造虚拟光笔。

图7 图像处理方法

将构造的不同DFB虚拟光笔的距离参数代入到1.3节所述的系统模型中进行算法处理，获得光笔探头中心在相机坐标系中的坐标(x0, y0, z0)。依据图7所示的图像处理方法，对30个位置的光笔各进行50次稳定性实验，计算所得到的系统测量结果——(x0, y0, z0)的标准方差。此外，为了验证相机光轴与光笔F面及B面的夹角对测量结果的影响，将相机放置在两个不同的位置进行对比实验：光笔正对相机光轴与光笔偏离相机光轴0.8 m，对这两种情况分别进行处理。稳定性实验结果如图8所示。

上述实验中，相机距离第一个位置的光笔一直保持在2 m左右。为了验证相机与光笔之间的距离对测量结果的影响，使用第i个位置的标号5～10的LED所成像与其后30-i个位置的标号1～4的LED所成像(i=1，2，…20)，构造不同DFB距离的虚拟光笔。同样将其参数代入到系统模型中，依据图7所示的图像处理方法，进行50次稳定性实验，计算测量结果的标准方差。稳定性实验结果如图9所示。由于篇幅限制，这里只给出最后两个位置的处理结果。

从图8与图9的虚拟光笔稳定性实验结果中，可得到如下结论：

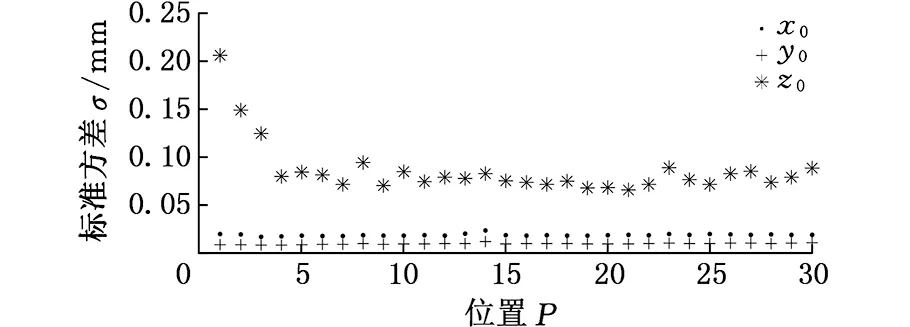
(a)光笔正对相机光轴

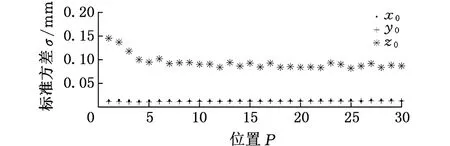
(b)光笔偏离相机光轴0.8 m

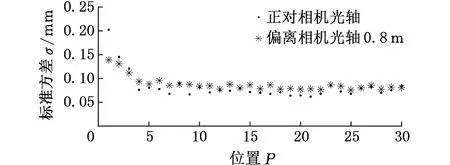
(c)光笔正对/偏离相机光轴z0方向稳定性比较

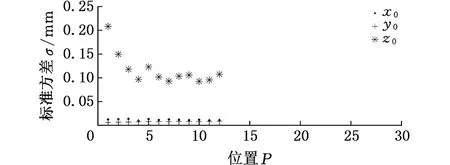
(a)光笔正对相机光轴(第十九位置)

(b)光笔偏离相机光轴0.8 m(第十九位置)

(c)光笔正对相机光轴(第二十位置)

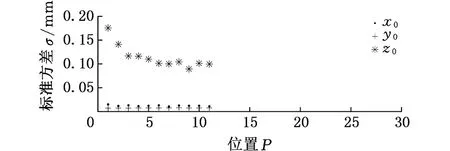
(d)光笔偏离相机光轴0.8 m(第二十位置)

(1)在系统三个方向测量稳定性中，相机光轴方向即Z轴方向的测量稳定性要比相机坐标系的另外两个方向即X轴、Y轴方向的稳定性差很多，而X轴方向和Y轴方向的测量稳定性基本相同。

(2)X轴、Y轴方向的测量稳定性基本不受距离参数DFB的影响，而Z轴方向的测量稳定性随着距离参数DFB增大而提高。初始时探头中心Z轴方向稳定性实验结果的标准方差急剧下降，在第五个位置(DFB=80 mm)左右下降速度减慢，随后保持小幅度波动。

上述实验中，虽然只将相机放置在正对光笔与偏离光轴0.8 m这两个位置，但考虑到实际测量时，光笔F面与B面与相机光轴方向的夹角一般不大(夹角过大时，LED所成像中心定位时的椭圆中心畸变误差将增大，影响系统测量精度及稳定性)，因此可以满足实际要求。而虚拟光笔距离相机的位置只变化了20个位置(320 mm)，但实际测量过程中，本系统中光笔与相机的距离变化也不大(光笔与相机之间的距离越远，LED所成像越小，其中心定位精度会降低，而系统测量精度也会随之降低)，所以也可以满足要求。因此认为上述结论不受相机与光笔之间相对位置的影响。

3.2 精度对比实验及结果分析

为了验证3.1节中的结论，分别使用现有光笔与虚拟光笔(DFB=80 mm)在CMM平台上进行了三组精度对比实验。实验流程如下：如图4所示放置光笔与相机，使光笔随着CMM主轴在其X、Y、Z坐标轴方向上各运动100，100，50 mm(CMM的Z轴可运动行程较短)，共5次，每个位置均采集10幅图像。

实验结果如表1所示，使用虚拟光笔(DFB=80 mm)的系统测量精度(三个坐标轴方向上的测量误差分别为-0.037 mm,-0.772 mm,0.002 mm)要优于使用现有光笔的精度(三个坐

表1 精度对比实验 mm

标轴方向上的测量误差分别为-0.082 mm,-0.946 mm,-0.006 mm)，而使用前者的系统测量稳定性也要优于使用后者的测量稳定性(极差为最大值与最小值之间的差值)。

4 结语

本文对光笔的结构参数即光笔控制点的空间分布对系统测量精度和稳定性的影响问题进行了深入的研究，而该问题的本质是光笔控制点在光笔坐标系中的坐标(ui,vi,wi)(i=1，2，…，10)对系统方程组求解公式(式(4))求解精度的影响。本文对系统中采用的光笔结构进行了分析，重点研究了不同的光笔前6个控制点所在面与后4个控制点所在面的距离对系统测量稳定性的影响。本文利用CMM主轴运动的高精度、高稳定性，构造了不同DFB距离参数的虚拟光笔，并进行了相机正对光轴与偏离光轴0.8 m以及当相机与光笔之间的距离不同时虚拟光笔稳定性实验，得出最优的DFB是80 mm。为了验证此结论，使用现有光笔与虚拟光笔(DFB=80 mm)在CMM平台上进行了三组精度对比实验，实验结果表明使用虚拟光笔(DFB=80 mm)能够提高现有系统的测量精度及测量稳定性。

虽然实验中得出的最优DFB距离与实验时的其他参数有关，如相机焦距、光笔结构其余尺寸等，当这些参数发生改变后，这个距离参数可能不再是最优值，但上述结论证明了光笔结构参数对系统测量稳定性有着直接的、显著的影响，为未来光笔结构的优化设计提供了一个重要的参考依据。

[1] 黄风山.光笔式单摄像机三维坐标视觉测量系统关键技术的研究[D].天津：天津大学，2005.

[2] Liu Shugui, Peng Kai, Huang Fengshan, et al. A Portable 3D Vision Coordinate Measurement System Using a Light Pen[J]. Key Engineering Materials, 2005, 295/296(1):331-336.

[3] Zhang Xiaofang, Jiang Chengzhi, Xue Tongze, et al. The Light Pen of a No Guide 3D-coordinate Measuring System[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2006, 635742:1-9.

[4] Zhang Fengshou, Jin Jianli, Li Xikai. Research on Light Pen Measuring System[J]. Key Engineering Materials, 2012, 522:490-494.

[5] 张晓芳，俞信，蒋诚志，等.无导轨空间坐标测量系统的光笔优化设计[J].北京理工大学学报，2003，23(6)：744-748。 Zhang Xiaofang, Yu Xin, Jiang Chengzhi, et al. Optimization Design of Light Pen for Use in Space Coordinate Measuring Systems without Guideway[J]. Transactions of Beijing Institute of Technology, 2003, 23(6):744-748.

[6] 秦大辉，毛婷，刘建军.基于双目立体视觉的手持式光笔三坐标测量系统[J].制造技术与机床，2011(8)：133-136。 Qin Dahui, Mao Ting, Liu Jianjun. Study on 3D-coordinate Measurement Technology Using Handhold Light-pen Based on Binocular Stereoscopic Vision System[J]. Manufacturing Technology & Machine Tool, 2011(8):133-136.

[7] 刘书桂, 姜珍珠, 董英华，等.采用移动光靶标的分区域相机标定[J].光学精密工程, 2014, 22(2)：259-265。 Liu Shugui, Jiang Zhenzhu, Dong Yinghua, et al. Sub-regional Camera Calibration Based on Moving Light Target[J]. Optics and Precision Engineering, 2014, 22(2): 259-265.

[8] 徐士良，马尔妮.常用算法程序集(C/C++描述)[M].5版.北京：清华大学出版社，2013。

[9] Liu Shugui, Zhang Hongling, Dong Yinghua, et al. Portable Light Pen 3D Vision Coordinate Measuring System-probe Tip Center Calibration[J]. Measurement Science Review, 2013, 13(4):194-199.

(编辑 王艳丽)

Design of Probe Structure in CMM System Based on Virtual Light-pen

Zhang Rui1Liu Shugui1Zhang Xin2Wang Youfu2

1.State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin,3000722.Jiujiang Precision Measuring Technology Research Institute,Jiujiang,Jiangxi,332000

Based on the virtual light-pen, a new type of light-pen structure was built by analyses of the system model’s feature. The light-pen adopted in the system had ten control points, and supposed the distance between the front plane where six control points laid and the back plane where other four ones did asDFB. The CMM’s main axis could move with high accuracy and stability, then virtual light-pens with different values ofDFBwere built. The structure model for the virtual light-pen was given in detail. And several experimental results prove that the parameterDFBremarkably affects the stability of the whole system with thatDFB’s optimal value is as 80 mm.

light-pen coordinate measuring machine(CMM); design of probe structure; measuring accuracy; virtual light-pen

2016-01-29

国防科工局技术基础渠道科研项目(JSJL2014206B001)

TH122

10.3969/j.issn.1004-132X.2016.24.009

张 瑞，男，1988年生。天津大学精密仪器与光电子工程学院博士。主要研究方向为智能坐标测量系统。发表论文4篇。刘书桂，男，1954年生。天津大学精密仪器与光电子工程学院教授、博士研究生导师。张 新，男，1982年生。九江精密测试技术研究所工程师。王有富，男，1967年生。九江精密测试技术研究所高级工程师。