三种空化模型在氧泵诱导轮中的计算分析

姜映福，刘中祥，褚宝鑫

（北京航天动力研究所，北京100076）

三种空化模型在氧泵诱导轮中的计算分析

姜映福，刘中祥，褚宝鑫

（北京航天动力研究所，北京100076）

为探索不同空化模型对氧泵诱导轮的适应性，选取Schnerr&Sauer，Zwart及Singhal三种空化模型对氧泵诱导轮进行数值模拟，将三种不同流量系数（φ=0.9，φ=1.0及φ= 1.1）下每个计算结果与实验数据进行对比，发现Schnerr&Sauer和Zwart两种模型预测空化外特性变化趋势更加接近实验值，其中Schnerr&Sauer模型在空化发生段的计算结果与实验结果吻合较好。Schnerr&Sauer和Zwart两种模型在φ=1.0的临界空化数与实验值误差为2.9%，在φ=1.1的临界空化数与实验值误差为8.7%，Singhal模型计算结果偏差较大。三种空化模型在计算叶片压力分布上比较相近，在计算叶栅及流道气泡数分布上，由于Schnerr& Sauer和Zwart模型都考虑了气泡数密度的影响，而Singhal模型仅考虑了气泡运动，计算的气泡分布较低；综合考虑外特性及内流场计算结果，Schnerr&Sauer更适应于诱导轮空化计算。

空化模型；数值分析；诱导轮

0 引言

诱导轮作为提高离心泵空化性能的有效途径被广泛应用于航空航天及石油化工领域［1］。随着液体火箭发动机技术指标的不断提高，入口条件日益恶化，诱导轮空化、振动及压力脉动等引发的故障比例越来越高。

空化是一种气液相间质量传输的非定常可压多相流动现象，它是流道内局部压力低于饱和蒸汽压而产生气泡、在高压区破灭消失的过程［2-4］；对很多装置的性能有着很重要的影响，比如泵、文氏管、钝头体和导流片。空化不仅会导致离心泵性能和效率下降，还会产生振动、噪声和损坏过流部件等一系列不利现象［5］。

计算流体动力学（CFD）可以有效地模拟诱导轮内部流动。空化计算主要采用正压状态方程的单流体模型［6-7］和基于相间传输的均相流模型［8-9］。大多空化模型是基于Rayleigh-Plesset方程的相间传输模型［10］。Kubota将Rayleith-Plesset方程耦合到求解器，提出了基于气泡动力学的两相模型，通过添加不同源项来调节气液两相间的传输［11-12］。Singhal在“全空化模型”中考虑了不可压缩气体的影响以及湍动能引起的压力脉动对空化的影响［13］。Schnerr&Sauer将水、汽的混合物看作是包含大量球形蒸汽泡的混合物，并直接从气液质量传输率的表达式入手，对其中的体积分数项进行了计算［8］。Zwart在Kubota和Gerber模型的基础上对质量空化率方程中的蒸汽的体积分数项进行了修正［9］。

本文针对商业软件Fluent中的三种空化模型Singhal，Schnerr&Sauer及Zwart，对某型氧泵进行数值模拟并与实验数据进行对比，讨论三种空化模型对低温泵空化性能计算的适应性。

1 数学模型

1.1 控制方程

定常条件下不可压流体的控制方程用以下方式表示：

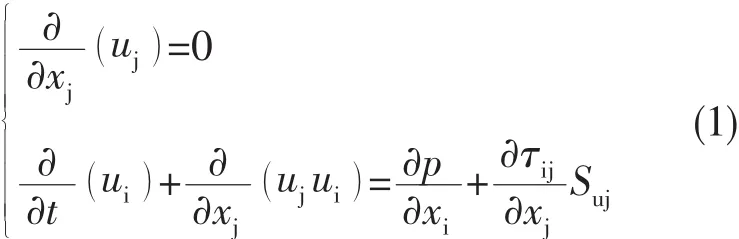
1.2 空化模型

蒸汽输运方程：

式中Re和Rc分别为蒸汽的生成项和凝聚项，记Sv＝Re-Rc为输运方程的源项。

将空泡动力学的经典理论Rayleigh-Plesset方程引入空化模型，方程如下：

式中：pB为气泡内压力；RB为空泡半径；σ为表面张力。

忽略二阶导数项和表面张力系数，方程简化为

1.2.1 Singhal模型

Singhal模型［13］是由Singhal开发的“全空化模型”，采用等温计算并考虑了相变，气泡运动，湍流压力波动和不可凝气体对气相生成率和凝结率的影响。

相变率的表达式为

式中：Fvap和Fcond为两个经验常数，分别选取Fvap＝0.02和Fcond＝0.01；k为湍动能。

1.2.2 Zwart模型

Zwart［8］模型假定所有气泡大小相同，认为相间的质量输运率由气泡数密度决定：

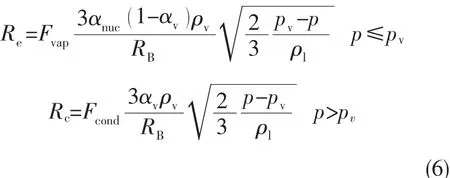
式中：气泡半径RB=10-6m；气核体积分数αnuc= 5×10-4；蒸发系数Fvap=50；凝聚系数Fcond=0.01。Fvap和Fcond差距大的原因是凝结过程比蒸发过程慢很多［8］。

1.2.3 Schnerr&Sauer模型

Schnerr&Sauer［9］模型将气泡数密度与气相体积分数耦合在一起进而对输运方程进行求解。直接从气液净质量传输率的表达式入手，对其中的体积分数项进行了计算：

式中空泡数密度n=1013左右。

1.3 湍流模型

本文选用非直接数值模拟中的双方程模型Realizable k-ε模型，此种模型已被有效地用于各种不同类型的流动模拟。近壁处理采用标准壁面函数法。

Realizable k-ε模型的湍动能及其耗散率输运方程［14］为

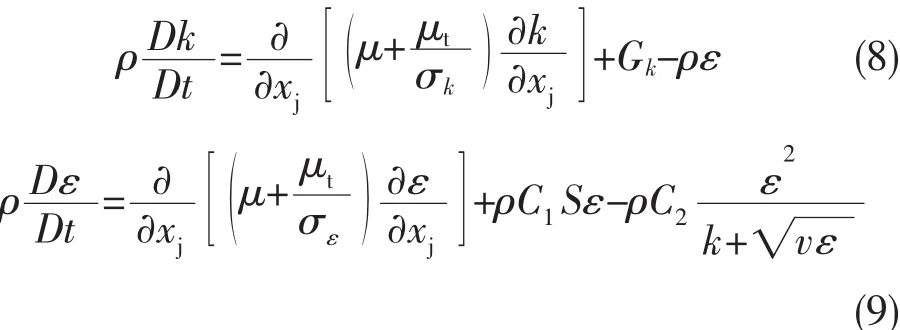
在上述方程中：C1ε＝1.44，C2=1.9，σk＝1.0，σε＝1.2。

2 研究对象及计算方法

2.1 研究对象

本文以某型氧泵为研究对象，主要分析诱导轮空化特性。泵的过流部件由诱导轮、导流支座、叶轮、带扩压叶片的蜗壳及泵壳体等组成，如图1所示。

图1 离心泵结构示意图Fig.1 Structure scheme of centrifugal pump

计算区域由进口延伸段、诱导轮、导流支座、叶轮、蜗壳及出口延伸段6部分组成。添加进出口延长段是为了减小较大的进出口速度梯度对计算结果精度的影响，一般选取3～5倍管道直径。其中诱导轮和离心轮为转子域，其余为静子域。

使用ANSYS Meshing划分网格，采用适应性较好的非结构网格，局部加密，进出口选用结构化网格，网格总数156万。

2.2 数值计算方法

本文选用基于有限体积法的Fluent软件，结合Singhal，Zwart和Schnerr&Sauer三种空化模型，采用Mixture两相流模型，选用Realizable k-ε双方程湍流模型，近壁面处理选用标准壁面函数法。以水为介质，其中20℃水的饱和蒸汽压为3 540 Pa。由于离心泵组件较多，内部流动相对复杂，求解方法采用coupled算法；而对于Singhal模型则选用SIMPLEC算法收敛较好［15］。为了使计算结果更好的收敛，本文首先计算未加空化模型的流场结果，其作为初始化条件加到空化模型计算。

进出口边界条件采用总压进口和质量流量出口条件，计算过程中通过调节入口压力来模拟空化过程；进口处液相和气相的体积分数分别为1和0；固体壁面采用绝热无滑移边界条件。

2.3 参数定义

为了便于处理数据，定义如下参数：

式中：uz和u2分别为泵入口轴向速度和叶轮出口圆周速度，m/s；H为泵扬程，m；r为泵入口半径，m；g为重力加速度，m/s2；ρl为液体密度，kg/m3；pin和pv分别为泵进口总压和饱和蒸汽压，Pa。

3 计算结果分析

3.1 不同空化模型下空化性能曲线

图2所示为不同流量下三种空化模型计算的离心泵空化性能曲线。

图2 不同流量系数下不同空化模型离心泵数值计算值与实测值的对比Fig.2 Comparison between calculated values by different cavitation models and measured values at different flow coefficients of centrifugal pump

从图2可以看出，三种流量系数状态下，σ＞0.015时，扬程基本恒定，泵中空化程度很小；0.01＜σ＜0.015时，扬程下降较快，泵中已经出现一定程度的空化；σ＜0.01时，扬程迅速下降，泵中空化程度急剧增大。不同流量系数条件下，三种空化模型都基本能预测到空化数减小到一定程度时泵扬程系数的急剧下降。φ=0.9时，未空化条件下Schnerr&Sauer模型和Singhal模型扬程系数ψ基本相同，在空化曲线拐点处有一定差距，而Zwart模型相比前两种扬程系数ψ较低，但均高于实验结果。而0.01＜σ＜0.015时，对应的Schnerr&Sauer模型计算外特性变化趋势与实验结果最接近。与φ=0.9，φ=1.1相比，φ=1.0时，三种模型计算结果与实验最接近；其中Schnerr &Sauer模型和Zwart模型扬程系数ψ变化趋势基本相同，Singhal模型计算结果扬程系数ψ相比较低，在0.01＜σ＜0.015区间，Schnerr&Sauer模型和Zwart模型相对结果较好。φ=1.1时，其中Schnerr&Sauer模型和Zwart模型扬程系数ψ变化趋势基本相同，而Singhal模型计算结果扬程系数ψ与Schnerr&Sauer模型和Zwart模型相比较高，同样在0.01＜σ＜0.015区间，前两种空化模型的空化曲线与实验结果更接近。

一般认为泵扬程下降2%时，诱导轮完全空化，通过插值计算得出泵扬程下降2%对应的临界空化数，各模型临界空化数的计算值与实验值对比如下表1所示。

由表1可知，在φ=0.9时，Singhal模型的临界空化数与实验值较接近；φ=1.0和φ=1.1时，Zwart和Schnerr&Sauer模型的临界空化数与实验值的偏差相同，其中φ=1.0时，两种模型的临界空化数的误差较小为2.9%；φ=1.1时，两种模型的临界空化数的误差为8.7%；φ=0.9时，偏差较大。

表1 诱导轮临界空化数数值计算值与实验值对比Tab.1 Contrast between critical cavitation values from different cavitation models and measured values of inducer

Zwart模型假设气泡大小相同，相间的质量输运率由气泡数密度决定；Schnerr&Sauer模型直接从气液净质量传输率的表达式入手，将气泡数密度与气相体积分数耦合在一起。二者都考虑了气泡数密度的影响，且计算精度较高，收敛速度较快。Singhal模型考虑了气泡运动，湍流压力波动和不可凝气体对气相生成率和凝结率的影响；但计算过程稳定性较差，收敛难度大。

扬程的数值模拟计算结果与实验数据有差别是因为：数值计算没有考虑实验条件等造成的摩擦损失及CFD计算软件的不完善等造成。

3.2 不同空化模型下诱导轮内流场分析

下面选取φ=1.0流量工况对三种空化模型计算诱导轮内空化流场进行详细分析。

3.2.1 二维叶栅空化分布

当诱导轮局部压力低于介质饱和蒸汽压时，就会产生空泡。图3为φ=1.0流量工况下不同空化数时span=0.7切面上叶片间的空泡体积分数分布（其中span定义为诱导轮轮毂到轮缘的无量纲距离，取值范围为0～1）。

图3 不同空化模型不同空化数时二维叶栅空泡体积分数分布Fig.3 Vapor volume fraction distributions calculated by different cavitation models at different cavitation values of 2D blade cascade of inducer

从图3可以看出，当σ=0.013时，可以观察到叶片吸力面进口边开始有空泡附着在叶片上，随着空化数σ的减小，空泡首先出现在靠近叶尖部分的低压区，吸力面空泡体积分数逐渐增大，并沿轴向叶片出口发展，直到布满整个流道。span=0.7切面上，Schnerr&Sauer和Zwart模型σ=0.01时流道开始堵塞，当σ=0.009时，空泡几乎完全充满叶片间流道，这直接影响液流的正常流动，此时诱导轮完全空化，导致泵的性能严重降低；而对于Singhal模型，叶片间含气区域扩大速度较慢，且叶片气泡分布极少，当σ=0.01时，泵扬程下降2%，诱导轮扬程下降15%，诱导轮完全空化，而流道气泡分布仍极少。Schnerr &Sauer和Zwart模型都考虑了气泡数密度的影响，而Singhal模型仅考虑了气泡运动。

3.2.2 轴向空化分布

诱导轮轴向空化分布即诱导轮入口到出口流域沿轴向方向截面的空化区分布，如图4是φ=1.0流量工况下三种空化模型在不同空化数下的含气率分布。空化数越小，空化区在流域分布越宽，最大含气率越高；三种空化模型都是在轴向0.5位置处开始出现气泡，这与诱导轮吸力面叶尖处最先产生气泡对应；随着空化发展，空泡向出口处发展，σ=0.008时，诱导轮整个流道都存在气泡。同样Singhal模型的含气率与Schnerr &Sauer和Zwart模型相比极少。

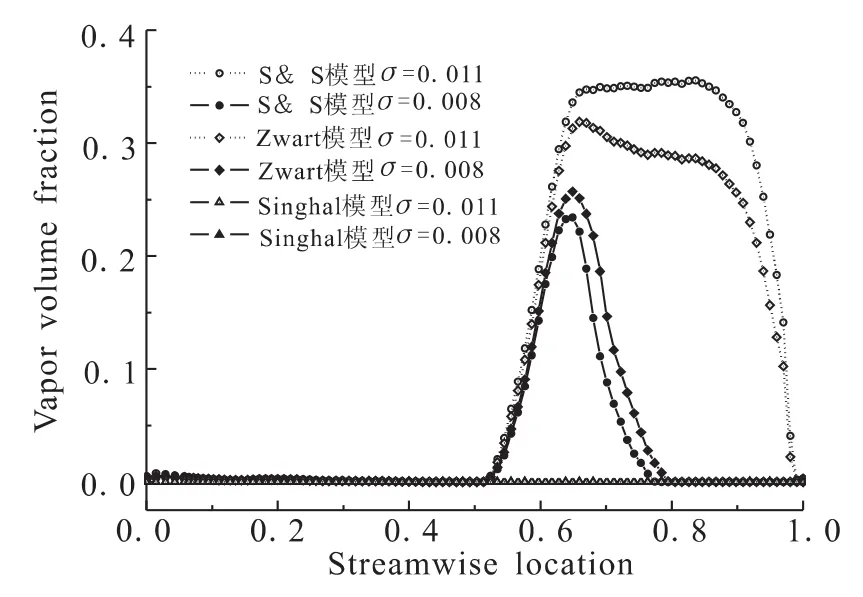
图4 诱导轮内沿轴向方向各截面平均含气率Fig.4 Average vapor volume fraction of each cross section along axial direction in inducer

3.2.3 叶片压力分布

为更直观分析诱导轮空化性能，给出了诱导轮在未空化、空化发生和完全空化时叶片吸力面的压力分布，其中未发生空化和空化发生时压力分布基本相同。入口压力较高时，低压区首先在叶片吸力面叶尖部分和叶片打薄区的顶部；随着入口压力降低，低压区向叶片尾部发展。当压力下降到σ=0.009时诱导轮完全空化，压力分布如图5所示，低压区布满整个叶片。

图5 不同空化模型叶片吸力面压力分布Fig.5 Pressure distribution of blade suction surface of different cavitation models

从图5中可以看出，空化数σ较大时，三种模型的诱导轮低压区相近，均首先出现在叶片吸力面靠近进口边的叶尖部分，这正是最易发生空化的部位；随着空化数降低，低压区逐渐向叶片尾部发展。

随着空化数的降低，Singhal模型低压区的扩大速度最慢，Schnerr&Sauer模型最快。当σ= 0.011时，三种方案的低压区分布范围相近。在σ=0.009时，Schnerr&Sauer模型的低压区已经几乎布满整个叶片，诱导轮发生完全空化；而Zwart模型和Singhal模型叶尖尾部仍有增压能力。

4 结论

1） 将三种空化模型在诱导轮的空化性能数值计算与实验对比，发现三种模型均能正确的预测出空化数减小到一定程度时扬程的下降。Zwart和Schnerr&Sauer两种模型空化外特性预测趋势更加接近实验值，其中Schnerr&Sauer模型对汽蚀发生段的预测更加准确；φ=1.0时Zwart和Schnerr&Sauer的临界空化数的误差较小为2.9%，φ=1.1时，临界空化数的误差为8.7%，Singhal模型计算结果与实验偏差较大；综合考虑，Zwart和Schnerr&Sauer两种模型相对Singhal模型能够更加准确的预测诱导轮的空化外特性。

2） 分析额定流量下三种空化模型计算的诱导轮空化内流场。当诱导轮流道被增长的空泡填充时，叶片吸力面流场的扰动更加突出，导致流动与叶片分离，因而扬程下降。空化数降低到一定值时，空泡布满整个流道，诱导轮扬程急剧下降。三种空化模型低压区分布及压力变化相近；由于Schnerr&Sauer和Zwart模型都考虑了气泡数密度的影响，而Singhal模型仅考虑了气泡运动，计算的叶栅及流道的含气率极低，明显不符合实际情况，因此在气泡数分布上，前二者的计算结果较为准确。

［1］马相孚.低温流体空化特性数值研究［D］.哈尔滨：哈尔滨工业大学，2013.

［2］关醒凡.现代泵理论与设计［M］.北京：中国宇航出版社，2011.

［3］柯乃普.空化与空蚀［M］.水利水电科学研究院（译）.北京：水利出版社，1981.

［4］JACKSON J K.Liquid rocket engine turbpump inducers：NASA SP-8052［R］.USA：NASA，1971.

［5］WANG Yong，LIU Houlin，YUAN Shouqi，et al.Experimental testing on cavitation vibration and noise of centrifugal pumps under off-design conditions［J］.Transactions of the Chinese Society of Agricultural Engineering（Transactions of the CSAE），2012，28（2）：35-38.

［6］ESFAHANIAN V，AKBARZADEH P，HEJRANFAR K.An improved progressive preconditioning method for steady non-cavitating and sheet-cavitating flows［J］.International journal for numerical methods in fluids，2010，68（2）：210-232.

［7］POUFFARY B，FORTES-PATELLA R，REBOUD J L，et al.Numerical simulation of 3D cavitating flows：Analysis of cavitation head drop in turbomachinery［J］.Journal of fluids engineering，2008，130（1）：8-14.

［8］SCHNERR G H，SAUER J.Physical and numerical modeling of unsteady cavitation dynamic：ICMF 2001［R］. New Orleans，USA：［s.n.］，2001.

［9］ZWART P J，GERBER A G，BELAMRI T.A two-phase flow model for predicting cavitation dynamics：ICMF 2004［R］.Yokohama，Japan：［s.n.］，2004.

［10］沈天耀.离心叶轮的内流理论基础［M］.杭州：浙江大学出版社，1986.

［11］KUBOTA A，KATO H，YAMAGUCHI H.a new modeling of cavitating flows：a numerical study of unsteady cavitation on a hydrofoil section［J］.Journal of fluid mechanics，1992，240（1）：59-96.

［12］KUBOTA A，KATO H.Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling techniques［J］.Journal of fluids engineering，1989，111（3）：204-210.

［13］SINGHAL A K，ATHAVALE M M，HUIYING L，et al. Mathematical bases and validation of the full cavitation model［J］.ASME journal of fluids engineering，2002，124：617-624.

［14］王福军.计算流体力学分析［M］.北京：清华大学出版社，2004，120-132.

（编辑：马 杰）

Numerical simulation and analysis of three cavitation models for liquid oxygen pump inducer

JIANG Yingfu，LIU Zhongxiang，CHU Baoxin
（Beijing Aerospace Propulsion Institute，Beijing 100076，China）

In order to explore the adaptability of different cavitation models to the liquid oxygen pump inducer，three cavitation models（Schnerr&Sauer model，Zwart model and Singhal model）were selected to simulate the liquid oxygen pump inducer numerically.The simulation results were compared with the experiment results respectively under the condition of three different flow coefficients（φ=0.9，φ=1.0，φ=1.1）.It is found that the prediction accuracy of Schnerr&Sauer model and Zwart model is higher than Singhal model.Among them，the calculation results of Schnerr&Sauer cavitation model in the section of cavitation occurrence are in good agreement with the experiment results.As φ=1.0，the error between the experimental value and the critical cavitation number of Schnerr&Sauer model and Zwart model is 2.9%；as φ=1.1，the error between them is 8.7%；the error of calculated result from Singhal model is larger.The blade pressure distribution values calculated bythe three models are similar.while simulations of vapor volume fraction distribution among blades section with different cavitation number were different.When calculating the contribution of blade cascade and bubble number in flow path，the effect of bubble number density was considered in Schnerr&Sauer model and Zwart model，but the bubble motion onlywas considered in Singhal model. Thus，bubble distribution calculated by Singhal model is relatively low.In consideration of the external characteristics and the inner flow field calculated results，the Schnerr&Sauer model is more suitable for the calculation ofinducer cavitation.

cavitation model；numerical analysis；inducer

V432-34

A

1672-9374（2016）05-0017-05

2016-03-23；

2016-05-19

姜映福（1990—），男，硕士，研究领域为低温汽蚀