基于扰动观测器的无人水面船鲁棒轨迹跟踪

朱齐丹， 马俊达， 刘可

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

基于扰动观测器的无人水面船鲁棒轨迹跟踪

朱齐丹， 马俊达， 刘可

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001)

为实现三自由度无人水面船(USV)在风浪流引起的海洋环境干扰下的轨迹跟踪，设计一种非线性扰动观测器(NDO)和动态面控制(DSC)的鲁棒控制器。首先，提出一种新的NDO来在线估计并补偿外界环境干扰。与传统干扰观测器不同，该扰动观测器具有有限时间收敛的特点；然后，在运动学回路中利用反演法设计虚拟控制律来镇定跟踪误差，并其通过一阶低通滤波器避免了由对虚拟控制求导而带来的计算复杂性，同时通过NDO对未知海洋干扰进行实时补偿，利用Lyapunov稳定性定理证明了USV闭环系统的误差信号半全局最终一致有界(SGUUB)。最终，仿真实验证明了所设计控制策略的有效性。

鲁棒控制；非线性扰动观测器；动态面控制；无人水面船；轨迹跟踪

0 引 言

近年来，USV(unmanned surface vehicle，USV)能够在无人操作情况下完成特定任务，目前已广泛应用在油气勘探、近岸监控、海底绘图等领域[1-2]。由于USV在海上航行时会受到未知风浪流等复杂海况的影响[3]，所以如何抑制外界干扰，实现对期望航迹的准确跟踪变得充满挑战。目前，除了基于线性简化模型的传统控制方法(如PID，LQG[4])，还有滑模控制[5]、Lyapunov直接法[6]、基于前馈估计器的鲁棒控制[7]、单层神经网络控制[8]等非线性控制手段应用于USV轨迹跟踪。

基于NDO(nonlinear disturbance observer，NDO)的控制方法能够增强系统扰动抑制能力，提高系统鲁棒性。目前，NDO广泛应用在机械臂控制[9]、导弹控制[10]、主动式悬架控制[11]、近空飞行器控制[12]以及船舶控制[13]等领域。传统扰动观测器(disturbance observer，DO)的设计与分析都是基于线性化模型或利用线性系统技术设计的[9]。然而，实际被控对象(如飞行器，船舶等)具有强耦合非线性的特点，利用线性手段进行DO的设计是不准确的。为此，文献[9]假设干扰时变速率慢于DO的动态特性，设计了可应用于非线性模型的DO，其估计误差具有指数收敛特性；文献[14]利用模糊逻辑系统能够任意逼近强非线性函数的特点设计了NDO；文献[15]利用被控对象提供有效信息及径向基神经网络的逼近能力设计了一种神经网络扰动观测器；文献[13]假设已知扰动变化率的上界，设计NDO能够使扰动估计误差以指数速度收敛于平衡点的球形领域内。以上文献提出的NDO共同缺点是估计误差的收敛速度较慢，仅仅取得了渐近收敛。

近些年，反演法作为有效的非线性控制手段成为研究热点，并与动态滑模[16]、级联系统理论[17]等方法结合应用于船舶控制领域。然而，反演法在设计过程中会对虚拟控制律求导，存在“计算膨胀”的问题[18]，增加了控制律的复杂程度。针对这个问题，文献[18]提出动态面控制(dynamic surface control，DSC)技术，在中间过程中增加了一阶低通滤波器，进而近似估计虚拟控制律的一阶导数，降低了控制系统复杂程度。

本文考虑USV非线性Coriolis项以及海洋环境干扰，利用有限时间理论设计一种新型NDO，并结合反演技术与DSC技术，提出了一种USV鲁棒控制策略，实现了控制策略的仿真验证。

1 问题描述

仅考虑水面三自由度，忽略USV在纵摇、艏摇及升沉方向上运动，得到USV非线性模型[3]

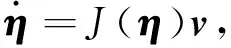
(1)

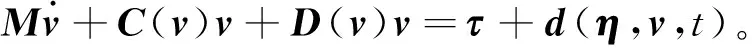
(2)

其中：η=(x,y,θ)T∈R3为USV姿态输出，用来表示在大地坐标系下船体的位置(x,y)与艏向角θ；v=(u,v,r)T∈R3为系统状态，表示船体坐标系的线速度以及角速度；J(η)表示USV体坐标系与大地坐标系之间的变换矩阵

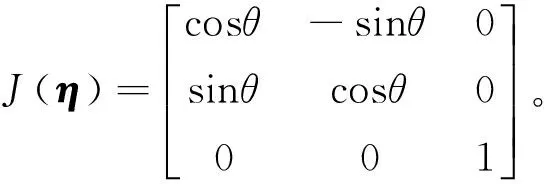
(3)

且满足||J(η)||=||JT(η)||=1，M表示含有附加质量的惯性矩阵，满足M>0；矩阵C(v)v表示Coriolis和向心力；矩阵D(v)v表示非线性阻尼力；M，C(v)和D(v)分别表示如下

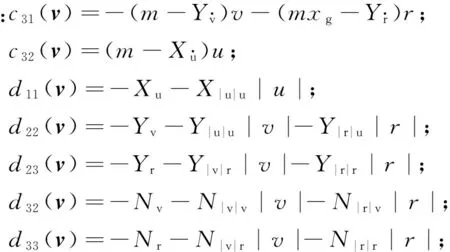
系数X(·),Y(·),N(·)表示水动力参数，具体含义可参照文献[23]。d∈R3表示由海洋风浪流产生的时变干扰力矩。

设USV参考轨迹为ηr(t)，给出以下假设：

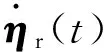
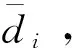
注1假设1保证参考轨迹足够光滑，从而避免了因轨迹跟踪误差突变而导致的不连续控制；由于海洋环境产生的能量是有限的，所以假设2是符合实际情况的。

在设计控制器之前给出以下定义：

定义1[21]针对系统

(4)

其中，f(·):Ω→Rn是关于自变量x的连续函数，x的定义域Ω是原点x=0的一个开邻域。如果系统的平衡点x=0是稳定的且在有限时间内收敛于原点的一个邻域Ω0⊆Ω，则称平衡点x=0是有限时间稳定的，即系统是有限时间稳定。有限时间收敛指存在函数T:Ω{0}→R+，对于任意x0∈Ω0，满足系统(4)的状态变量x(t,x0)在特定时间T(x0)内趋于x=0，且当t≥T(x0)时，x(t,x0)恒为零。进一步，如果满足Ω0=Ω=Rn，则上述系统是全局有限时间稳定的。

控制目标：在假设1与假设2成立的情况下，针对USV非线性模型(1)与(2)，设计基于NDO的鲁棒控制律τ，使得USV在风浪流干扰下实现对参考轨迹ηr(t)的稳定跟踪。

2 控制器设计

控制器设计共分两步：首先，针对USV非线性模型(1)与(2)设计NDO，实现对环境干扰的在线估计；然后，利用反演法对系统内环外环分别设计控制律，以NDO作为干扰的前馈补偿实现航迹控制。整个控制系统结构如图1。

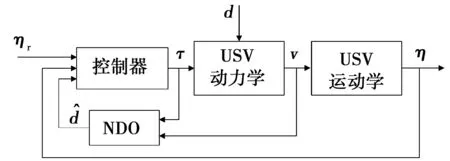
图1 控制系统结构图Fig.1 Block diagram of the control system

2.1 NDO设计

施加在USV动力学模型的外界风浪流扰动或者未建模动态特性会影响控制系统性能[3]，甚至导致系统发散。为此，基于USV非线性模型设计NDO来估计干扰，并将其反馈到控制律中，实现了对扰动的实时补偿。

在设计NDO之前，给出以下引理：

引理1[19]假设存在一个连续可微正定函数V(X):D→R满足

(5)

式中，原点的开邻域D0∈D，实常数c,l>0,α∈(0,1),则系统有限时间稳定，同时到达时间T(X0)满足不等式

(6)

若定义域D=Rn，不等式(5)在Rn/{0}均成立，则系统(1)全局有限时间稳定。

下面给出NDO的设计过程：

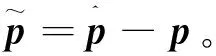
(7)

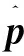
(8)

通过式(8)进一步得到干扰观测量

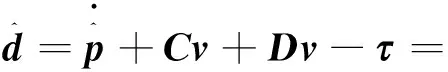
(9)

上述NDO设计可归纳为以下定理：

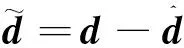
证明定义候选Lyapunov函数，如下

(10)

对式(10)两边求导可得

(11)

将式(2)与式(8)代入上式后得到

(12)

其中，D1min=min{D11,D12,D13}，D2min=min{D21,D22,D23}。

由式(7)～式(9)进一步得到

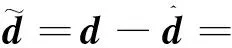
(13)

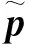
证毕

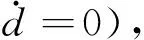
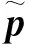
2.2 控制器设计

(14)

其中，τDSC待设计轨迹跟踪控制律。

将式(14)代入式(1)与式(2)得到

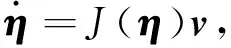
(15)

(16)

针对式(14)与式(15)设计τDSC：

Step 1 运动学回路设计

定义第1动态面

s1=η-ηr。

(17)

构造候选Lyapunov函数，如下

(18)

对式(18)两边同时求导可得

(19)

其中，αv为速度v虚拟控制律，满足ev=v-αv。

设计速度v的虚拟控制律αv

(20)

其中，控制参数矩阵K1为正定阵。

将式(20)代入式(18)，得

(21)

将虚拟控制律αv时间常数为T0的一阶低通滤波器，令vr表示滤波器输出，即

(22)

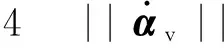
(23)

Step 2 动力学回路设计

定义第2动态面

s2=v-vr。

(24)

对式(24)两边同时求导可得

(25)

设计τDSC：

(26)

其中，K2>0表示控制参数矩阵。

2.3 稳定性分析

定义滤波器估计误差

ef=vr-αv。

(27)

上式结合式(20)得

(28)

对上式两边求导得

(29)

由式(17)、式(20)、式(24)、式(26)得

(30)

由式(24)、式(26)得

(31)

整理式(2)、式(7)、式(8)有

(32)

定理2考虑USV数学模型(1)(2)与鲁棒控制律(14)式(26)组成的闭环控制系统，若假设1与假设2成立，且初始条件满足V2(t0)≤p(p>0)，则通过调整控制参数K1,K2,T0,D1可使USV闭环控制系统所有信号满足SGUUB。

证明构造Lyapunov函数

(33)

对式(33)两边同时对时间t求导得

(34)

由式(29)式(30)式(31)式(32)可得

(35)

由Young不等式ab≤a2+0.25b2，结合式(29)、式(30)、式(31)得

(36)

将式(36)代入式(35)可得

(37)

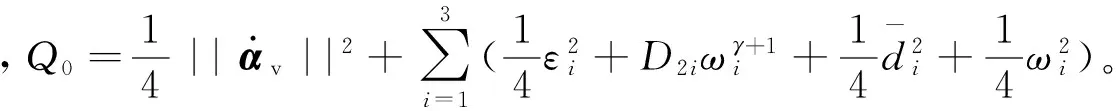
考虑以下紧集：

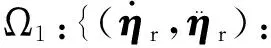
Ω2:{(s1,s2,ef):‖s1‖2+‖s2‖2+‖ef‖2≤2p}。

其中χ,p为正常数。显然Ω1×Ω2也是紧集。因此，注4中的连续函数f在Ω1×Ω2上有上界，记作|f|≤fmax。因此，

结合式(37)得

(38)

式中：

02;

λmin(K2)>1.25。

(39)

证毕

注5对式(38)两边同时在区间[t0,t]取积分，得

(40)

则有

(41)

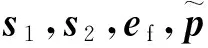
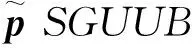
注7在运动学回路中，虚拟控制律αv的导数为

(42)

可以看出其包含众多变量，不利于实际应用。为此，利用DSC，将虚拟控制律通过一阶低通滤波器，避免了对虚拟控制律求导，减少了计算量。

3 仿真与分析

为说明本文提出方法有效性，本节以挪威科技大学海洋控制实验室1:70船模CyberShip2[20]为控制对象，其模型结构参照式(2)。

参考轨迹ηr由虚拟移动机器人产生，即

(43)

其中:ηr=[xr,yr,θr]T；ηr(0)=[0,0,0]T;

ur=0.6 m/s；vr=0.1 rad/s；

USV初始位置η(0)与速度v(0)为：

η(0)=[1.2,1.8,π/4]T,v(0)=[0,0,0]T；

观测器参数设为

D1=diag{2,2,2}；

D2=diag{1,1,1}；γ=0.6；

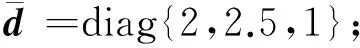
控制器参数设为

K1=diag{6,6,6}；K2=diag{1.4,1.4,1.4}；

时间常数为：T0=0.06。

下面分析控制系统在两种扰动下控制效果：

3.1 常值扰动下USV运动

3.2 时变扰动下USV运动

高级海况下的扰动力或力矩可以看成不同频率正弦信号的叠加。取扰动向量

d= [0.55+0.8sin(0.3t+π/6)+0.6×

sin(0.24t)N;0.8+0.9sin(0.5t+π/3)+

0.8cos(0.4t+π/4)N;0.5+0.1sin(0.1t)+

0.2cos(0.3t+π/6)N·m];

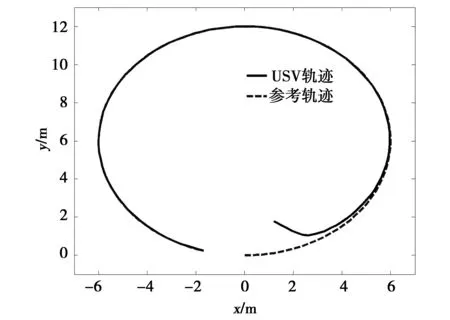
图2 常值干扰下USV运动轨迹Fig.2 Motion trace of the USV under constant disturbance

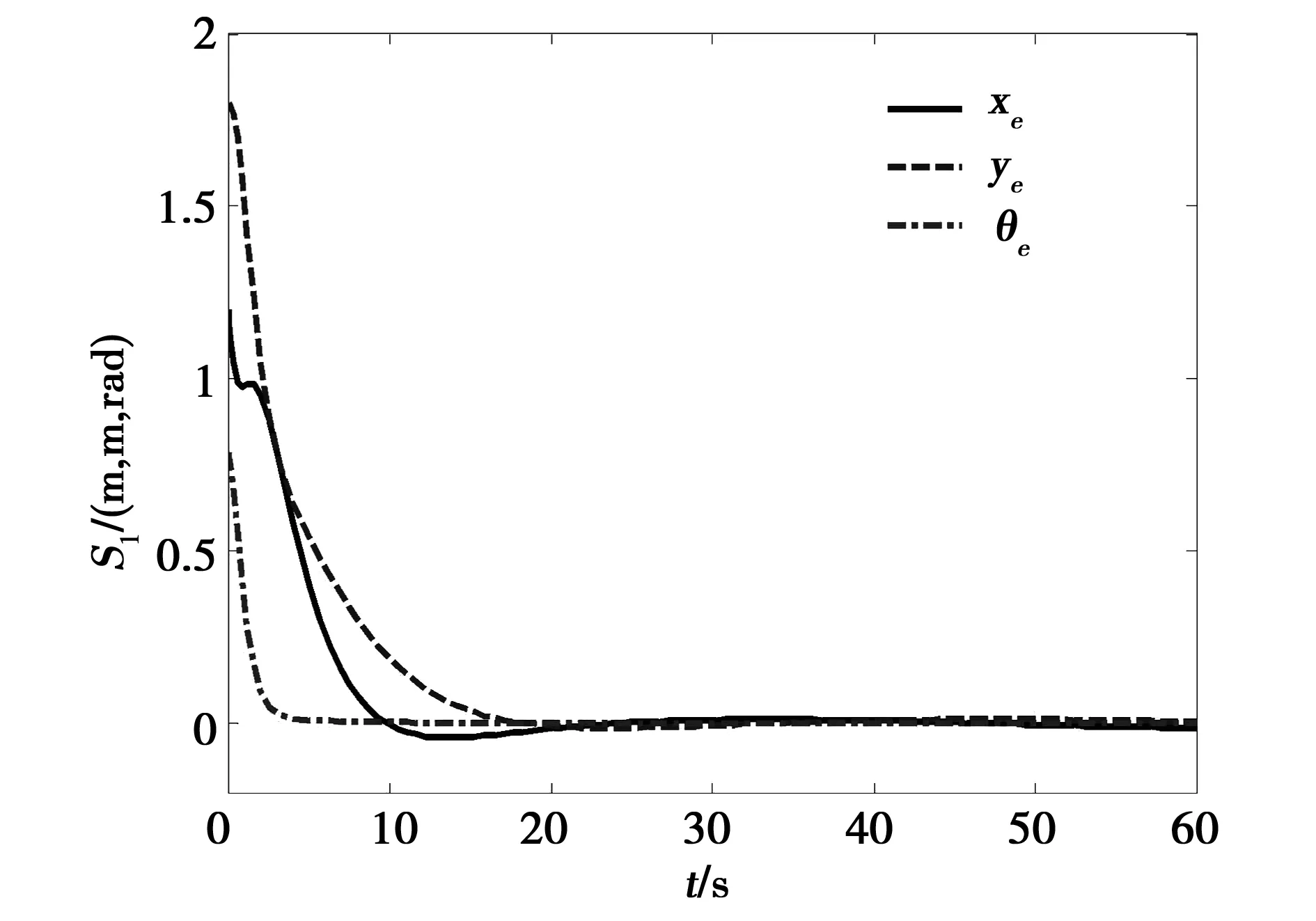
图3 常值干扰下USV跟踪误差Fig.3 Tacking error of the USV under constant disturbance

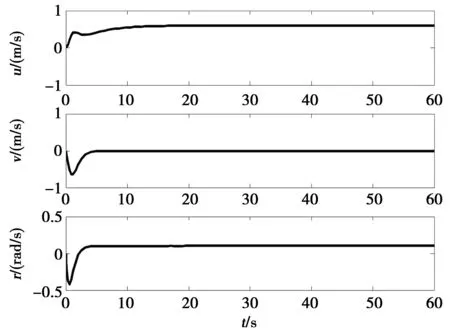
图4 常值扰动下USV速度Fig.4 Velocities of the USV under constant disturbance

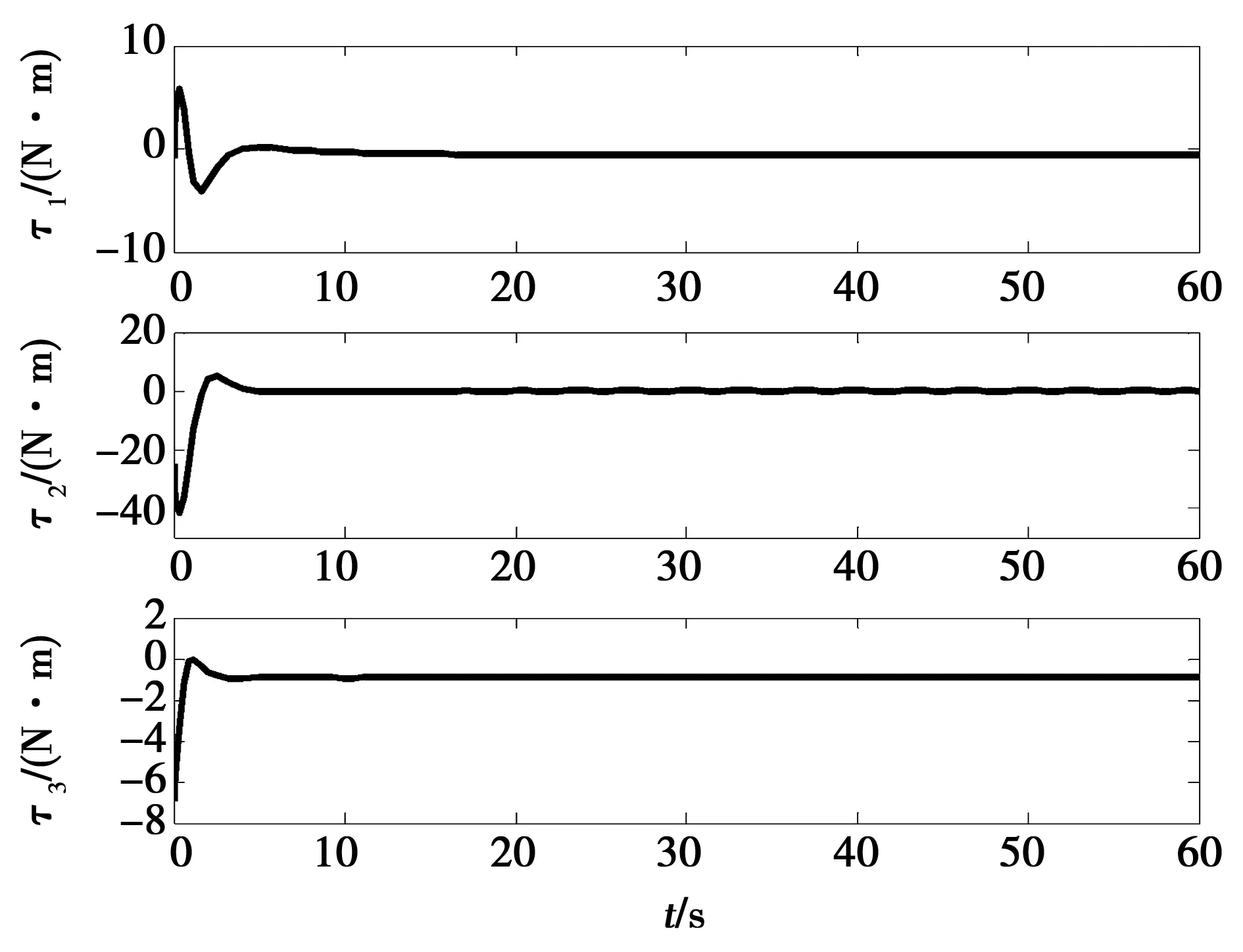
图5 常值扰动下控制输入τ1,τ2,τ3Fig.5 Control inpusts of the USV under constant disturbance

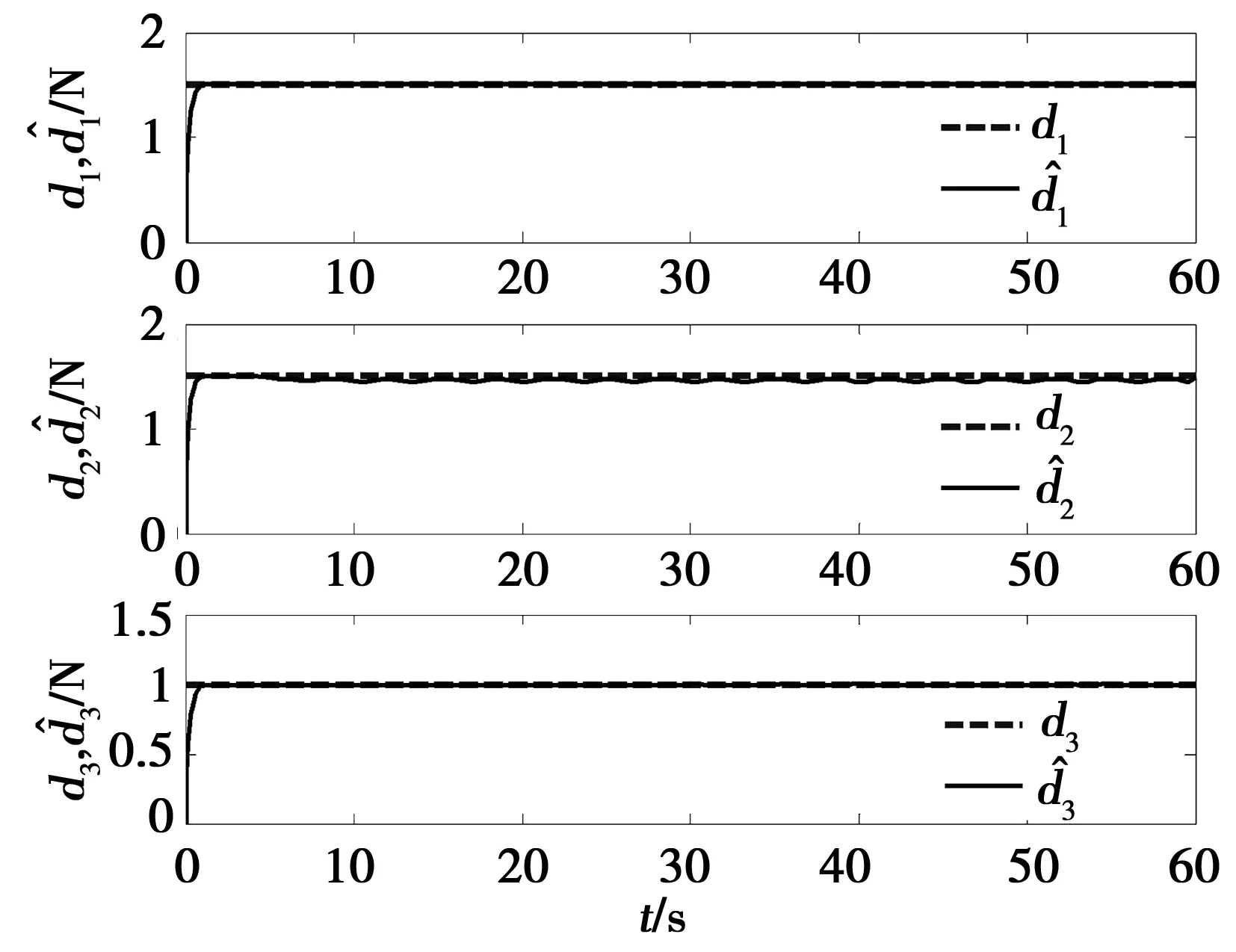
图6 常值干扰下外界干扰d1,d2,d3及其估计值Fig.6 Disturbances and their estimations of the USV under constant disturbance

USV在时变扰动下仿真曲线如图7～图11。从图7～图8可看出USV在时变扰动下也能实现对期望轨迹ηr的跟踪；由图10可知，在时变扰动下，USV各个轴向速度控制输入出现了一定幅度的摆动，这是因为控制律中包含着补偿外界干扰的扰动抑制项；图11显示本文设计的NDO在时变扰动下仍然能快速准确估计环境干扰。

3.3 与其它方法性能比较

本节将与文献[5]提出的滑模控制策略进行控制效果的比较。假设参考轨迹与环境干扰与上两节一致。取滑模控制[5]参数为

Λ=diag{5,0.4,1}；

W=diag{0.01,0.01,0.01}；

K=diag{2,14,1.5}。

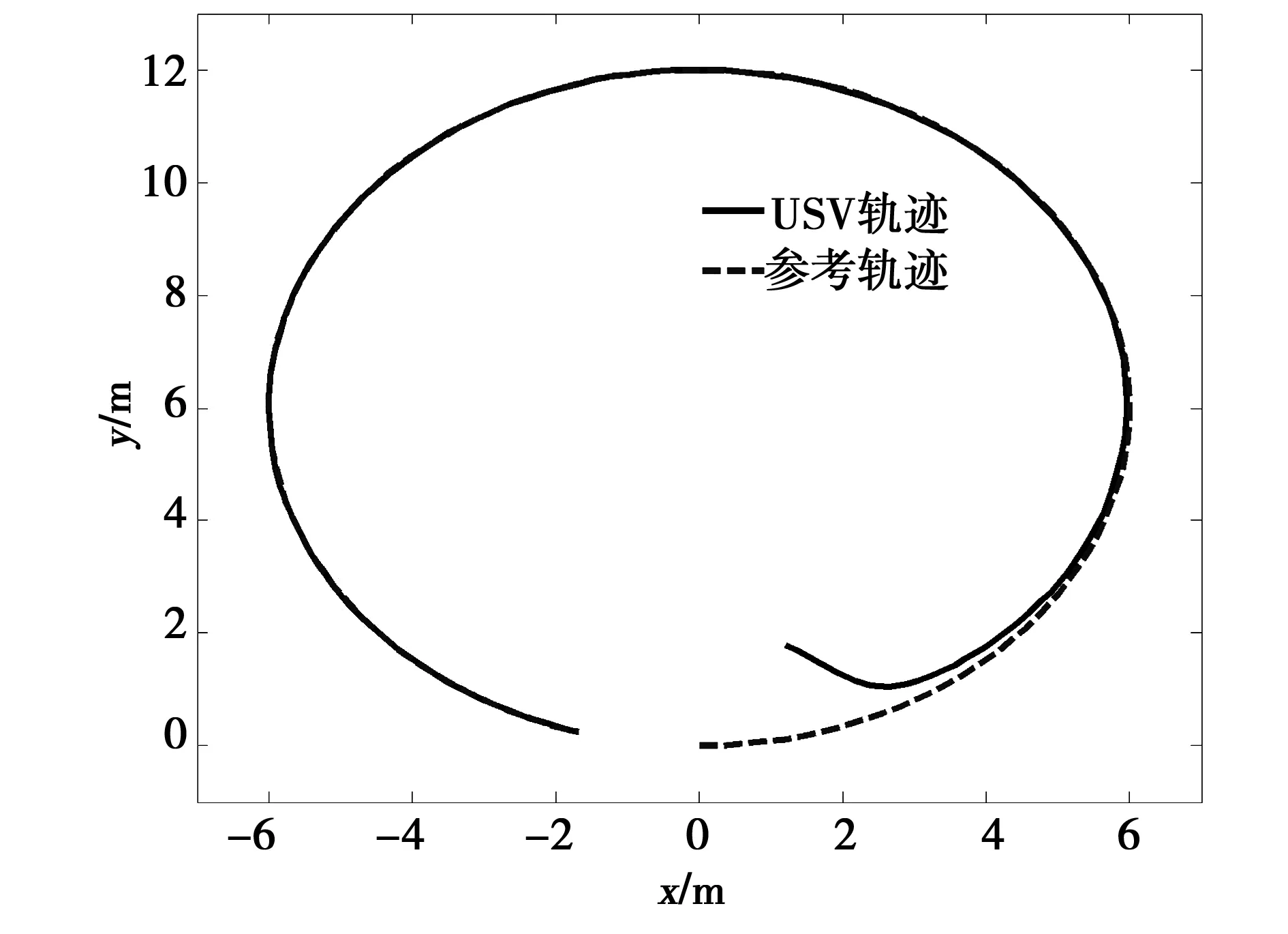
图7 时变干扰下USV运动轨迹Fig.7 Motion trace of the USV under time-varying disturbance

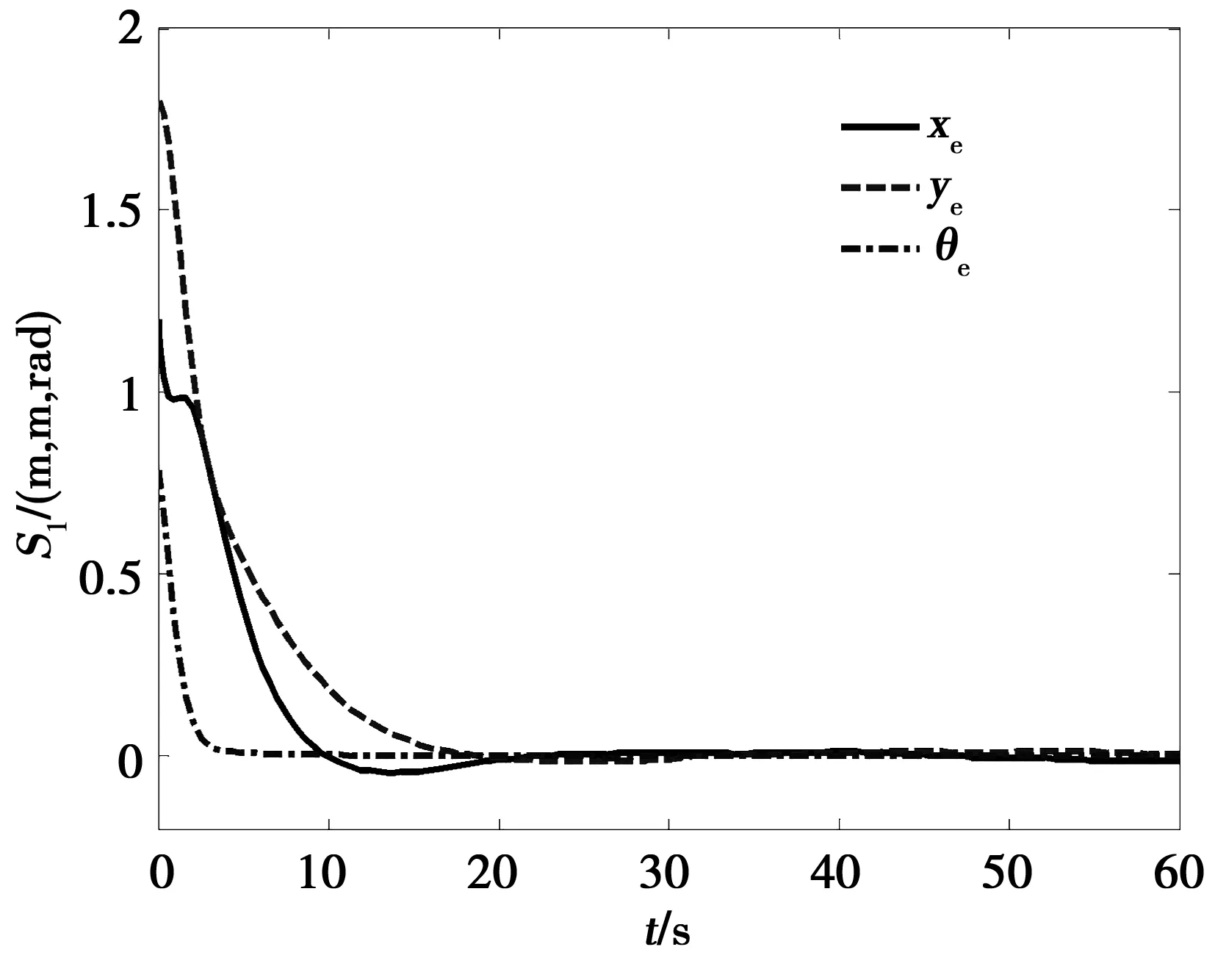
图8 时变干扰下USV跟踪误差Fig.8 Tracking errors of the USV undertime-varying disturbance

图9 时变扰动下USV速度Fig.9 Velocities of the USV under time-varying disturbance

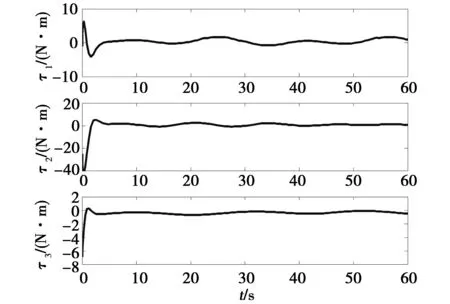
图10 时变扰动下控制输入τ1,τ2,τ3Fig.10 Control inpusts of the USV under time-varying disturbance

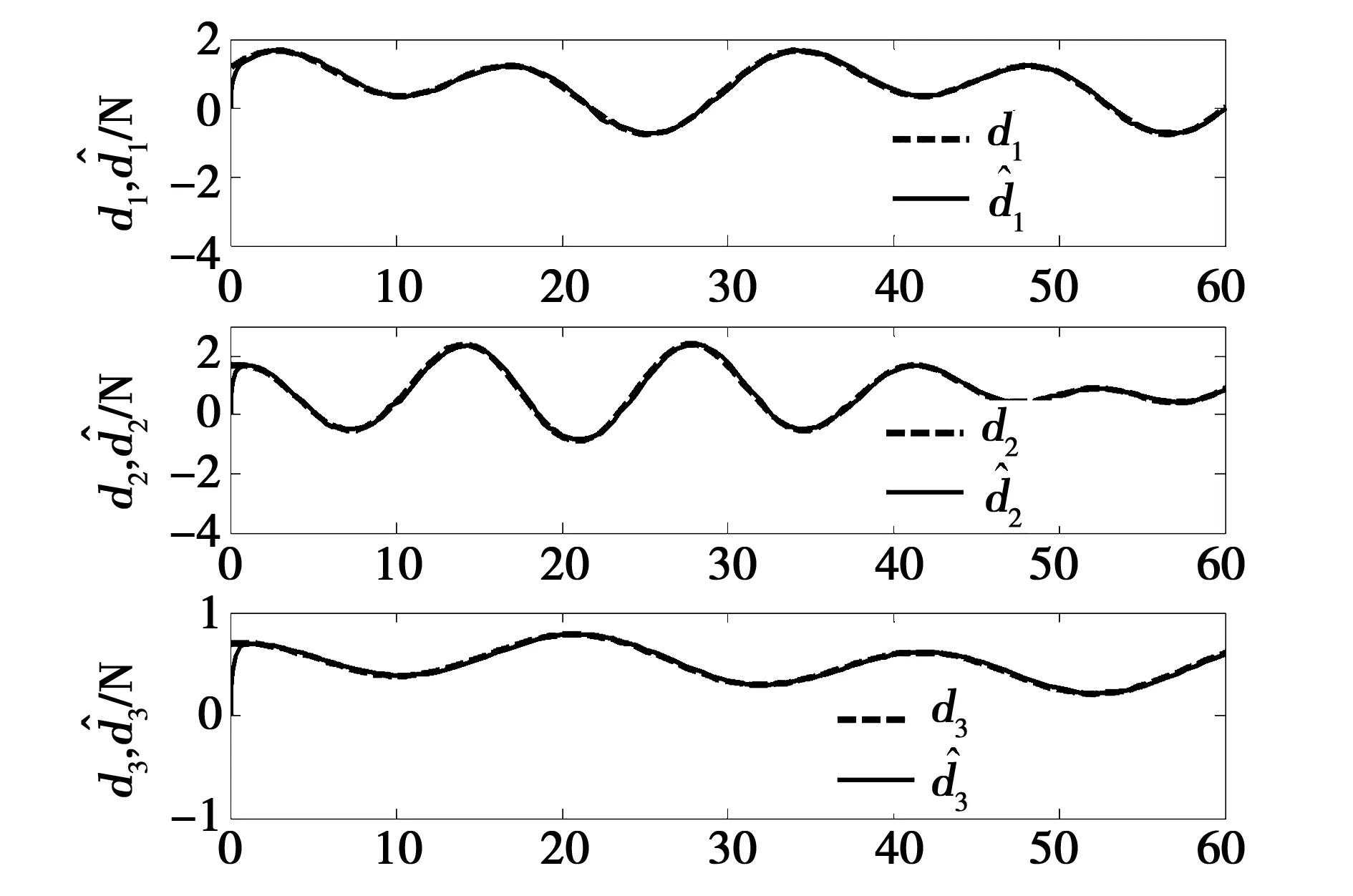
图11 时变干扰下外界干扰d1,d2,d3及其估计值Fig.11 Disturbances and theirestimations of the USV under time-varying disturbance

设轨迹跟踪误差eη=η-ηr，其2范数表示为‖eη‖。为了量化比较文献[5]和本文提出的控制策略，定义跟踪误差的绝对偏差积分[22](the integral of absolute error,IAE)，具体如下

(44)

其中td表示闭环系统的运行时间。

两种控制策略在不同扰动下的‖eη‖变化曲线如图12～图13，其对应运行时间的IAE值如表1所示。由图可知，由于滑模控制未有抑制扰动的措施，因而跟踪误差较大，且在时变扰动时出现大幅度波动；由于NDO对扰动的在线估计与补偿，本文方法跟踪误差更小。表1显示在同等运行时间下，本文设计控制策略下的IAE比文献[5]的数值小，说明基于NDO的控制策略具有更小的稳态误差。

综上可以看出，本文提出的鲁棒控制策略与文献[5]提出的滑模控制策略相比，跟踪误差相对更小，具有更高的控制精度与鲁棒性。

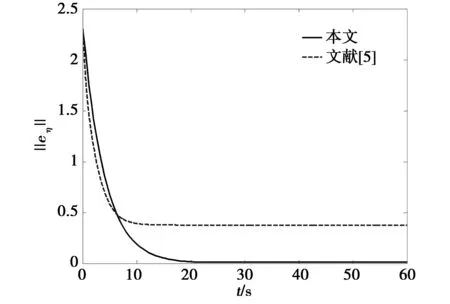
图12 常值扰动下USV各个方法的误差范数Fig.12 Error norms of the USV under constant disturbance

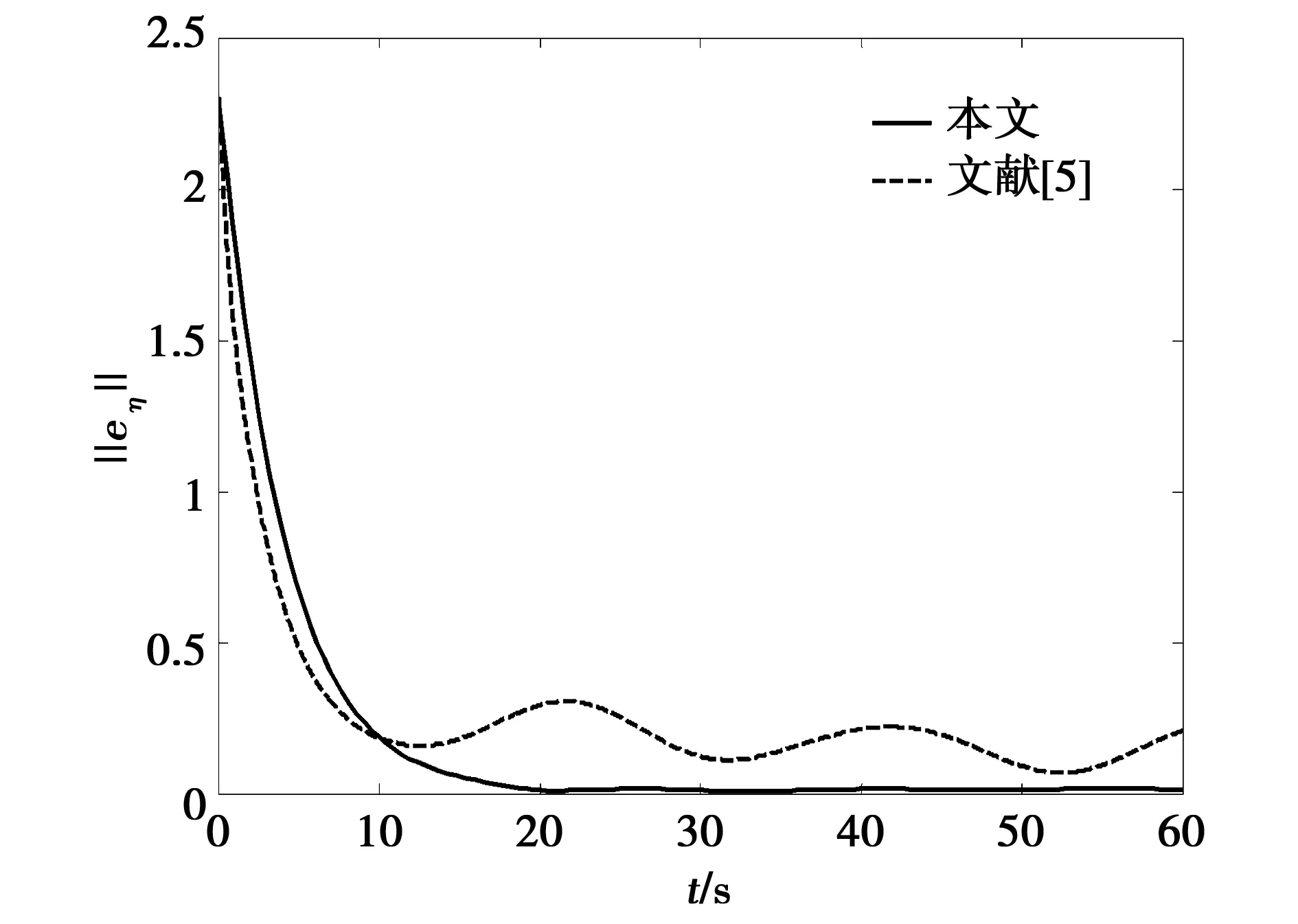
图13 时变扰动下USV各个方法的误差范数Fig.13 Error norms of the USV under time-varing disturbance

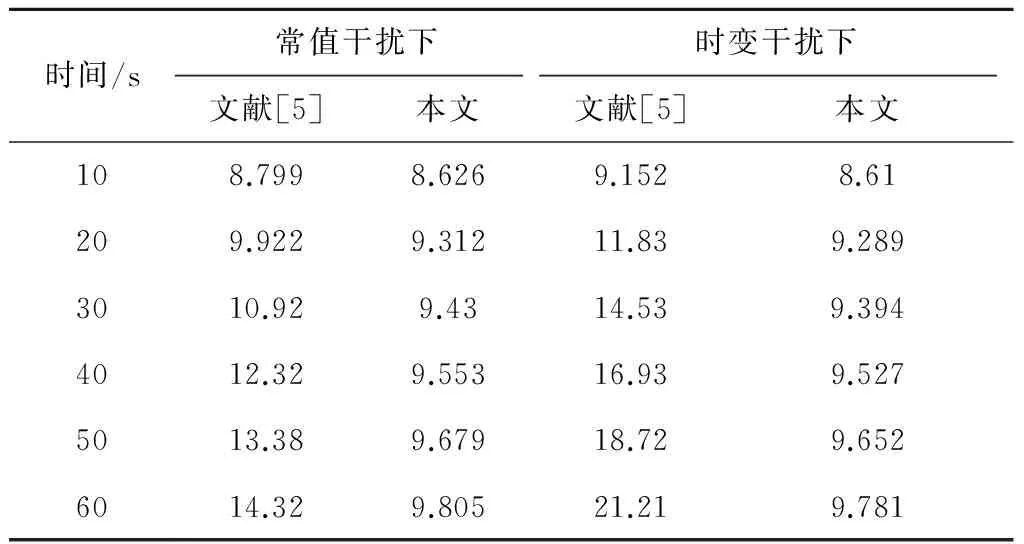
时间/s常值干扰下时变干扰下文献[5]本文文献[5]本文108.7998.6269.1528.61209.9229.31211.839.2893010.929.4314.539.3944012.329.55316.939.5275013.389.67918.729.6526014.329.80521.219.781

4 结 论

本文针对外界风浪流扰动下USV轨迹跟踪问题设计了一种基于新型NDO的动态面反演鲁棒控制策略。首先，为提高控制系统抗干扰性能，本文基于有限时间理论设计了一种新型扰动观测器，使得观测器能够在有限时间内趋近于外界干扰；然后，以NDO输出作为扰动补偿，基于反演法并利用DSC控制分别对运动环与动力环设计控制律，避免了对虚拟控制求导的繁琐计算，简化了控制器组成结构；最终，基于Lyapunov稳定理论证明了闭环系统信号SGUUB；针对船模型CyberShip2的仿真结果验证了该控制策略的有效性。

目前针对USV轨迹跟踪均为考虑控制输入的物理约束，这是未来值得研究的方向。

[1] BIBULI M,BRUZZONE G,CACCIA M.Path follow wing following algorithms and experiments for an unmanned surface vehicle[J].Journal of Field Robotics,2009,26(8): 669-688.

[2] YUH J,MARANI G,BLIDBERG D R.Applications of marine robotic vehicles[J].Intelligent Service Robotics,2011,4(4): 221-231.

[3] FOSEEN T I. Marine Control System[J].Trondheim,Norway: Marine Cybernetics,2002.

[4] HOLZHUTER T.LQG approach for the high precision track control of ships[J].IEE Proc.Control Theory Application,1997,144(2): 121-127.

[5] CHENG J,YI J,ZHAO D.Design of a sliding mode controller for trajectory tracking problem of marine vessels[J].IET Control Theory and Applications,2007,1(1): 233-237.

[6] JIANG Z P.Global tracking control of underactuated ships by Lyapunov direct method[J].Automatica,2002,38(2): 301-309.

[7] TEE K P,GE S S.Control of fully actuated ocean surface vessels using a class of feedfor-ward approximators[J].IEEE Transactions on Control Systems Technology,2006,14(4): 750-756.

[8] PAN C Z,LAI X Z,SIMON X Y,el at.An efficient neural approach to tracking control of an autonomous surface vehicle with unknown dynamics[J].Expert Systems with Applications,2013,40(5): 1629-1635.

[9] CHEN W H,BALLANCE D J,GAWTHROP P J,et al.A nonlinear disturbance observer for robotic manipulators[J].IEEE Transactions on Industrial Electronics,2000,47(4): 932-938.

[10] CHEN W H.Nonlinear disturbance observer enhanced dynamic inversion control of missiles[J].Journal of Guidance,Control,and Dynamics,2003,26(1): 161-166.

[11] DESHPANDE V S,MOHAN B,SHENDGE P D,et al.Disturbance observer based sliding mode control of active suspension systems[J].Journal of Sound and Vibration,2014,333(11): 2281-2296.

[12] 于靖,陈谋,姜长生.基于干扰观测器的非线性不确定系统自适应滑模控制[J].控制理论与应用,2014,(8): 993-999. YU Jing,CHEN Mou,JIANG Changsheng.Adaptive sliding mode control for nonlinear uncertain systems based on disturbance observer[J].Control Theory &Application,2014,(8): 993-999.

[13] DO K D.Practical control of underactuated ships[J].Ocean Engineering,2010,37(13): 1111-1119.

[14] KIM E.A fuzzy disturbance observer and its application to control[J].IEEE Transactions on Fuzzy Systems,2002,10(1): 77-84.

[15] 朱亮,姜长生,张春雨.基于径向基神经网络干扰观测器的空天飞行器自适应轨迹线性化控制[J].航空学报,2007,28(3):673-677. ZHU Liang,JIANG Changsheng,ZHANG Chunyu.Adaptive trajectory linearization control for aerospace vehicle based on rbfnn disturbance observer[J].Acta Aeronautica et Astronautica Sinica,2007,28(3):673-677.

[16] LIAO Y,WAN L,ZHUANG J.Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel[J].Procedia Engineering,2011,15: 256-263.

[17] GHOMMAM J,MNIF F,BENALI A,et al.Asymptotic backstepping stabilization of an underacttuated surface vessel[J].IEEE Transactions on Control Systems,2006,14(6): 1150-1157.

[18] SWAROOP D,HEDRICK J K,YIP P P,et al.Dynamic surface control for a class of nonlinear systems[J].IEEE Transactions on Automatic Control ,2000,45(10): 1893-1899.

[19] SONG Z,LI H,SUN K.Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique[J].ISA Transactions,2014,53(1): 117-124.

[20] SKEJETNE R,FOSSEN T I,KOKOTOVIC P V.Adpative maneuvering,with experiments,for a model ship in marine control laboratory[J].Automatica,2005,41(2): 289-298.

[21] DU H,QIAN C,FRYE M T,et al.Global finite time stabilization using bounded feedback for a class of non-linear systems[J].IET Control Theory and Applications,2012,6(14): 2326-2336.

[22] BAYRAMOGLU H,KOMURCUGIL H.Time-varying sliding-coefficient-based decoupled terminal sliding-mode control for a class of fourth order systems[J].ISA Transactions,2014,53(4):1044-1053.

[23] SNAME.The society of naval architects and marine engineers,“Nomenclature for treating the motion of a submerged body through a fluid”[J].Tech.Res.Bulletin,1950:1-5.

(编辑：刘素菊)

A nonlinear disturbance observer based on robust approach to the trajectory tracking of an unmanned surface vehicle

ZHU Qi-dan， MA Jun-da， LIU Ke

(College of Automation,Harbin Engineering University ,Harbin 150001,China)

A robust controller based on nonlinear disturbance observer(NDO) and dynamic surface control(DSC) for 3 degrees of freedom unmanned surface vehicle(USV) under the presence of ocean environmental disturbances is presented.Firstly,a NDO was constructed to estimate and compensate for the environmental disturbances online.Unlike conventional disturbance observers,the proposed NDO had the characteristics of finite time convergence.In the kinetic loop,a virtual control was designed to stabilize the tracking error by back-stepping technique.A first order filter was introduced to avoid the complexity of computation caused by the derivation of virtual control.NDO was adopted to compensate for unknown ocean disturbance.The Lyapunov stability theory shows that all the signals of the closed system are semi-global uniformly ultimately bounded(SGUUB).Finally,numerical simulation results are given to verify the practical feasibility of the proposed approach.

robust control; nonlinear disturbance observer; dynamic surface control; unmanned surface vehicle; trajectory tracking

2015-08-28

国家自然科学基金(51379044);黑龙江省自然科学基金(F200916);中央高校基本科研业务费(HEUCFX41304)

朱齐丹(1963—),男，博士，教授，研究方向为船舶控制、机器人控制； 马俊达(1988—),男，博士研究生，研究方向为自主水面船非线性控制、多船编队控制； 刘 可(1986—),男，博士研究生，研究方向为阵列信号处理、波束形成、自适应控制。

马俊达

10.15938/j.emc.2016.12.009

TP 273

:A

:1007-449X(2016)12-0065-09