基于EMD-SG和信息熵矩阵束的同步电机参数辨识

郭欣欣， 陆华才， 陈亚辉， 田丽

(1.安徽工程大学 电气工程学院，安徽 芜湖 241000；2.国家电力公司 河南省电力公司鹤壁供电公司，河南 鹤壁 458000)

基于EMD-SG和信息熵矩阵束的同步电机参数辨识

郭欣欣1， 陆华才1， 陈亚辉2， 田丽1

(1.安徽工程大学 电气工程学院，安徽 芜湖 241000；2.国家电力公司 河南省电力公司鹤壁供电公司，河南 鹤壁 458000)

为了解决工程实际中准确获得同步电机瞬态及超瞬态参数问题，提出经验模态分解与矩阵束算法相结合的新型同步电机参数识别法。该方法借助EMD对采集到的含噪短路电流信号进行分解，采用Savitzky-Golay滤波器对高频分量部分进行平滑降噪预处理，借此提高其信噪比；为较好识别短路电流模态阶数，将信息熵引入矩阵束并将此改进矩阵束算法用以提取预处理后的短路电流各分量的频率和阻尼，进而识别出同步电机的瞬态参数。同步发电机三相突然短路仿真与试验参数辨识结果均表明，该方法在信噪比低于24 dB时，仍能快速、精确地辨识同步电机参数。

参数辨识；同步电机；经验模态分解；信息熵；矩阵束算法

0 引 言

随着电网规模的扩大化、结构的复杂化、功能的智能化，同步电机作为电力系统的重要设备，其参数的快速、准确辨识对分析和计算电力系统的行为有着决定性的意义，美国等一些发达国家的电力部门甚至出台一系列标准，其中就规定要定期辨识和校验发电机及其控制器参数。因此准确获取同步电机的参数成为学者的关注点[1-5]。

为了准确辨识同步电机参数，文献[6]和文献[7]提出先利用小波对短路电流进行消噪，再分别利用扩展Prony算法和矩阵束算法对同步电机的参数进行辨识，提高了辨识的精度，但在实际应用中存在对小波基的选择问题。文献[8]提出将经验模式分解与Prony结合对同步电机参数进行辨识，文中使用强制降噪方法，选择部分固有模态函数(intrinsic mode function，IMF)而丢弃另外一些IMF，这种去噪方法把高频信息当噪声滤除。文献[9]引入一种阵列信号处理方法TLS-ESPRIT(总体最小二乘-旋转矢量不变技术)，该方法采用短路电流进行两次消噪处理，在信噪比(signal-noise ratio,SNR)较高的情况下(大于30 dB)，得到了具有高精度的辨识结果。但随着信噪比的降低(30 dB以下)，辨识精度急剧下降，从而使该方法在工程实践应用中受到了限制。

由以上研究成果，本文采用Savitzky-Golay(SG)滤波器对经验模态分解(empirical mode de- composition,EMD)的分量进行降噪(以下称之为EMD-SG降噪法)结合信息熵矩阵束算法，提出一种识别同步电机参数的新方法，其核心是利用EMD-SG对短路电流数据进行平稳化预处理，然后将已作滤波处理的IMF分量与未作处理的IMF分量进行重构，对重构的信号运用矩阵束算法进行辨识。模态阶数M是识别参数准确性的关键，为使矩阵束算法能够减少计算量、提高识别模态阶数精度，将信息熵[10-12]引入矩阵束进行模态阶数M识别。仿真和试验结果表明该方法对噪声不敏感，信噪比低于24 dB具有很高的辨识精度。

1 基本原理

1.1 EMD分解

Norden E.Huang等人针对非平稳信号提出了一种经验模态分解法(EMD)，它将复杂的信号分解成若干个按频率高低排列的IMF，每一阶IMF都反映了原始信号的动态特性。该方法从待解数据本身的局部极值特征尺度出发对数据进行分解。反映了数据自身的变化规律，具有很强的自适应性。克服了小波分析中要选取合适的小波基的困难，使该方法具有良好的自适应性，适合于对非线性、非平稳的信号进行线性化和平稳化处理。

信号按EMD方法进行分解的步骤如下[8,10,13-14]：

1)确定原始信号s(t)的全部极值点。

2)分别用三次样条函数连接所有极大和极小值点，作为信号的上、下包络线并计算包络线的平均值m(t)。

3)计算原始数据s(t)与m(t)的差值，记为c(t)。

4)判断c(t)是否符合IMF的两个条件。如果满足，则认为c(t)是从原始信号中分解出的一个IMF分量。如果不满足条件，则认为c(t)等于s(t)重复以上步骤直到满足条件为止，视为分解出了一个IMF分量c1(t)。

5)s(t)与第一阶IMF分量c1(t)之差作为新的原始信号，用同样的方法筛选出其它IMF，直至残差小于预定值或基本呈单调函数。

s(t)最终被分解为一组振荡的IMF与一个余项r 之和，即

(1)

EMD分解得出的R个IMF反映了信号的特征尺度，是信号内在模态特征的代表。残余项r(t)，预示信号的平均趋势。

1.2 EMD-SG去噪

一般来讲噪声与有用信号是不相关的，具有不同的频谱特性，通常随机噪声主要存在于低阶IMF分量中，如果在信号重构时将低阶IMF分量全部去除，仅仅保留高阶IMF分量和余项，则会去除大部分噪声的影响。然而，这样强制降噪方法同时将导致相应分量上的有用信号与噪声一起被滤除，造成信号失真。为了防止在去噪的同时滤除原有信号的一些有用成分，破坏信号的完整性，影响后续信号分析的准确性，将EMD与SG滤波联合设计改善信号的信噪比，即将短路电流分解为少量的内蕴模式函数分量IMF，对前R/2个IMF采用 SG滤波器对采样点数据的邻域进行高阶最小二乘运算拟合，得到的邻域内最佳值作为去噪后的数值[10]，然后将滤波处理过的前R/2个IMF分量与后R/2个未作处理的IMF分量进行信号重构，得到降噪后的信号。

1.3 信息熵矩阵束算法原理

1980年，Hua和Sarkar等人提出矩阵束(matrix pencil,MP)算法。由于其采用内积形式提高抗噪能力，获得了较好的效果。矩阵束算法是非迭代算法的一种，避免了迭代法的一些弊端，不存在累积误差的问题，而且运算量不高，是一种非常高效的数值计算方法。

设系统的响应可以表示如下：

y(t)= x(t)+n(t)=

(2)

其中：n(t)为系统噪声；x(t)为不含噪声的响应；y(t)为实际观测到的包含噪声的响应；T为最大观测时间；0≤t≤T；将上式离散化

(3)

其中：k=0,1,....,N-1，N为最大采样点数；n(kTs)为系统噪音；x(kTs)为真实信号组成；对第i个模态，Ri为振荡幅值，复频域算子si=-ai+jωi中的ai为衰减因子，ωi为振荡角频率；Ts为采样时间间隔；M为信号的阶数。

矩阵束算法[15-19]的步骤如下：

1)最大模态数M的确定。由采样序列y(kTs)(k,1,2,...,N-1)构造如下形式的(N-L)×(L+1)阶矩阵Y：

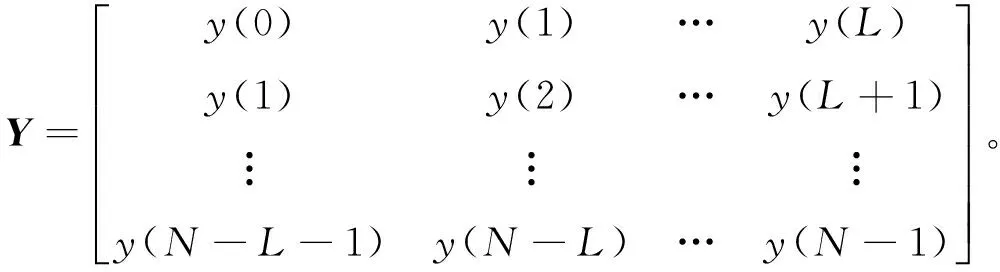
(4)

式中：L为矩阵束参数，适当地选择L可以抑制噪声的影响。一般情况下L取值范围N/4～N/3之间。

对矩阵Y进行奇异值分解

Y=UDVT。

(5)

式中：U为(N-L)×(N-L)的正交矩阵；V为(L+1)×(L+1)的正交矩阵；D为(N-L)×(L+1)的对角阵，其主对角元素σi为Y的奇异值。

若信号不含噪声，Y有q个非零奇异值σi(i=1,2,…q)，q的大小即为需要求解的最大模态数M。若信号存在噪声，则产生多余的虚假极点，D阵中原来为0者可能不再为0，所以应对奇异值应该进行截取，只保留其中M个最大的奇异值，以减小噪声对参数估计精度的不良影响。通常将满足σi/σi+1≤μ(μ为阈值)的最大下标记为最大模态数M。

为防止由于阈值设置不准确而造成矩阵束算法对模态阶数漏辨识或过辨识，将信息熵引入矩阵束进行最大模态M的确定。信息熵用来度量信息出现的概率，是对系统有序化程度的一种度量。

将pi定义为奇异值σi所占比重，奇异值的信息熵H(Y)可用下式进行表示：

(6)

(7)

σi值越小，所占比重越小，因此pi=0，pilg(pi)=0，H(Y)收敛至有界值；当奇异值为σm时，数值比较小，其信息熵很小，所给模态信息量比较少，因此模态阶数可以认为M=m。

同时由D的前M个非零奇异值形成如下形式的新阵D′,D′阵降低了噪声的影响。

(8)

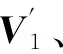
(9)

Y1、Y2已经消弱了噪声的影响。

3) 阻尼(衰减)因子和振荡角频率的求解。

由Y1和Y2构造矩阵束：

Y2-λY1=Z1R(Z0-λI)Z2。

(10)

式中：I为M×M阶单位阵

(11)

(12)

Z0=diag[z1,z2,…zM],

(13)

R=diag[R1,R2,…,RM]。

(14)

可以证明Y2-λY1的秩为M。而当λ同某极点zi相等时，矩阵Z0-λI的第i全为0，从而Y2-λY1的秩降为M-1。因此，信号的极点zi(i=1,2,3,…,M)就是矩阵束Y2-λY1的广义特征值，从而可以将求解信号极点的问题转化为求解矩阵Y2-λY1广义特征值的问题。即求解如下形矩阵G的特征值

(15)

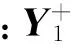
(16)

4)振荡幅值的求解。

最大模态数M及所有极点zi已知的情况下，幅值Ri可以利用以下最小二乘法计算：

(17)

2 发电机参数与三相短路电流

同步发电机突然三相短路时，A相定子短路电流标幺值表达式为

ia= i0(t)+i1(t)+i2(t)+e(t)=

Ecos(ωt+θ0)+e(t)。

(18)

式中：i0、i1、i2分别为短路电流的非周期分量、工频分量和倍频分量；e(t)为噪声电流，主要由饱和、涡流、磁滞等所引起的高次谐波电流和环境噪声组成，可以近似认为是一种白噪声。

噪声较强时，若直接对电流ia的采样数据利用矩阵束进行辨识，难以得到理想的结果。故首先利用EMD-SG对采样数据进行预处理，提高其信噪比。对处理后的短路电流采样值建立如下模型：

(19)

模型阶数M的确定是矩阵束算法中的一个关键。按提到的方法，阶数确定为7，即M=7。通过1.3节介绍的矩阵束算法，可求得各分量的幅值、初相位、阻尼以及频率，经计算[7]可得同步电机各待辨识的参数。

3 算例分析

3.1 仿真分析

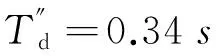
SRN=24 dB时同步电机三相突然短路电流波形如图1所示。

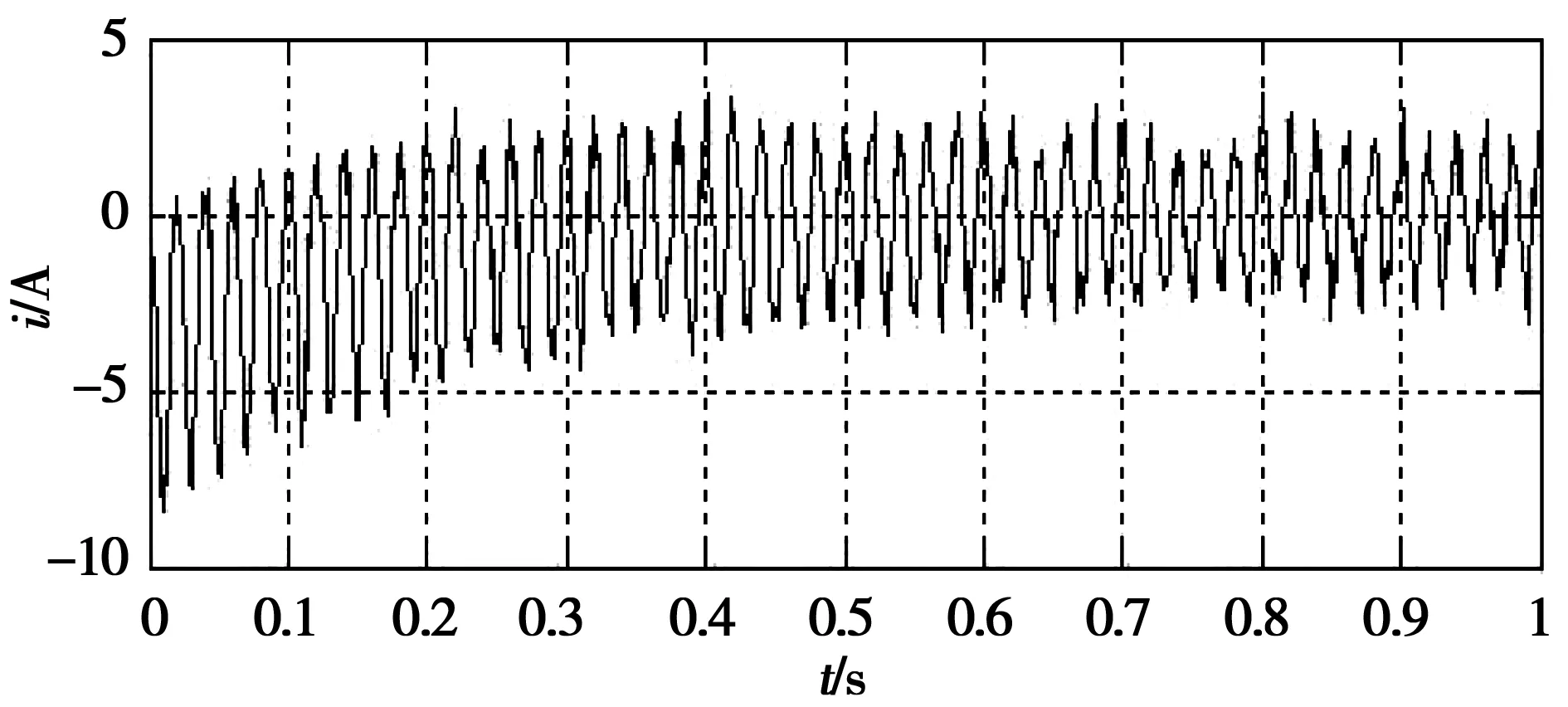
图1 SNR=24 dB短路电流波形图Fig.1 SNR=24 dB short-circuit current waveform

采样信号中含有高频噪声，用EMD将含噪声干扰的短路电流进行分解，得到8个IMF分量，如图2所示。考虑到EMD分解过程强迫分量相对零线对称，即自适应的对信号进行分解，因此简单的去掉一个或多个IMF分量以实现滤波，将导致相应分量上的有用信号一起被删掉了。从图2的EMD分解结果可以看出，第一个IMF分量imf1频率较高，幅值较小，疑似为噪声分量，为了确定成分是否属于噪声，可以对第一个分量进行相关分析。经分析第一个分量IMF分量与原信号的互相关不为零，因此不能直接删掉，以此类推。将前4个预处理后的IMF分量与后4个未处理的IMF分量进行信号重构。去噪后的短路电流信号如图3所示，可以看出信噪比得到改善，经测信噪比接近30 dB。

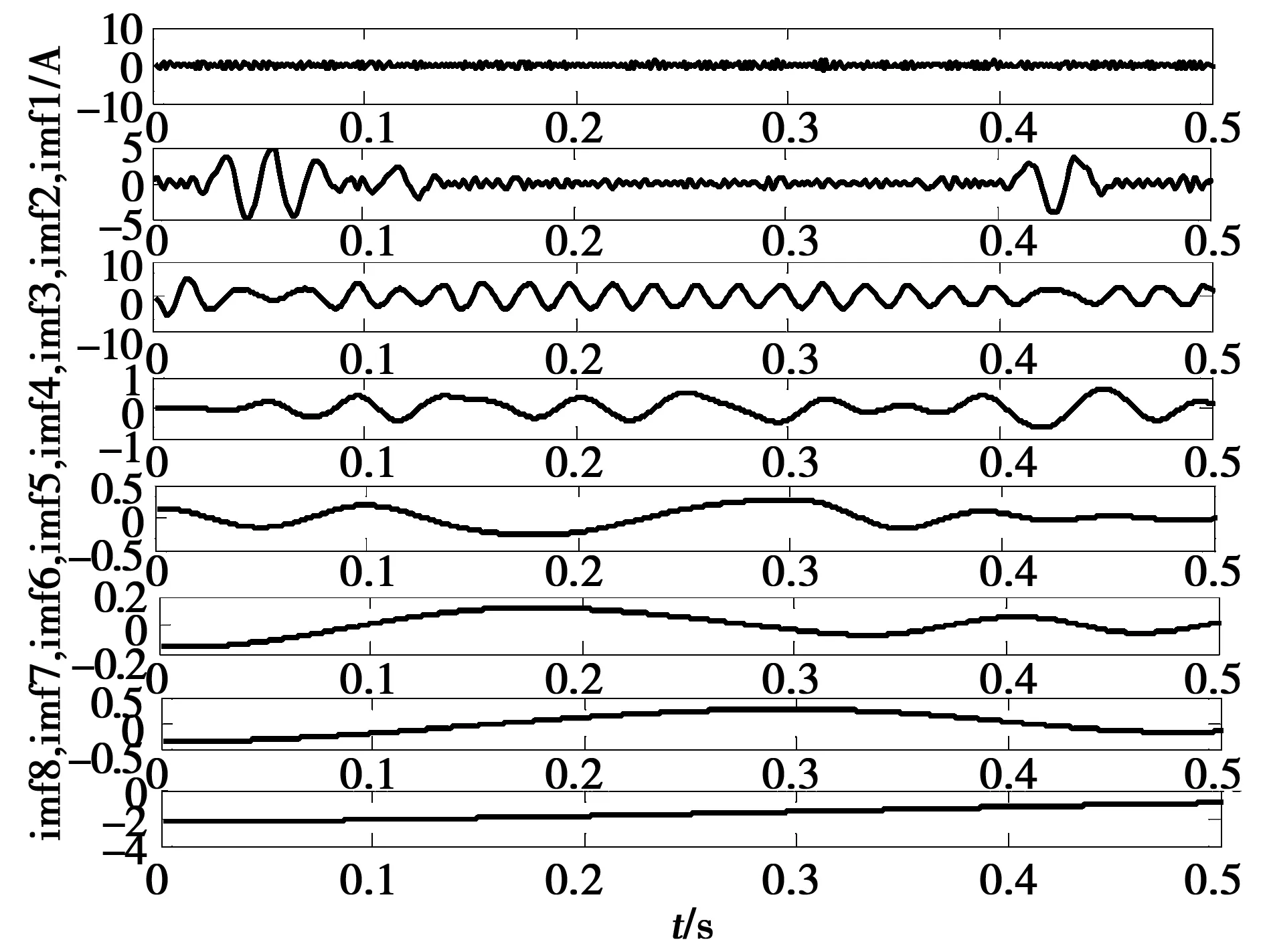
图2 短路电流EMD分解Fig.2 EMD decomposition of the short-circuit currents

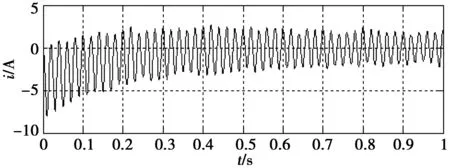
图3 经EMD-SG平滑处理后的短路电流波形Fig.3 Short-circuit current waveform of pretreatment

对去噪后的短路电流信号采用信息熵矩阵束算法进行辨识，辨识过程中将同步发电机的同步电抗xd当做已知量来进行处理。表1为本文方法提取的短路电流各分量的参数值，新算法对短路电流频率的辨识精度很高。为了量化辨识参数误差，这里引入相对均方误差[6]。表2给出了不同算法对同步电机参数辨识的结果,本文算法明显占优势，最高均方误差不超过3%。

表1 电流各分量参数提取量

从表2中不难看出，和Prony方法辨识得到的同步电机参数相比，Prony辨识误差普遍比较大，这可以从Prony算法抗噪性不强来解释；本文提供的同步电机参数辨识方法，辨识误差整体较低，最高误差不超4%，完全满足工程需求。表3给出了不同信噪比下，电机参数辨识对比结果。信噪比在15 dB时参数的最高均方误差仍不高于4%。

表2 两种方法电机参数辨识结果

Table 2 Synchronous generator parameters identification result bu two algorithms

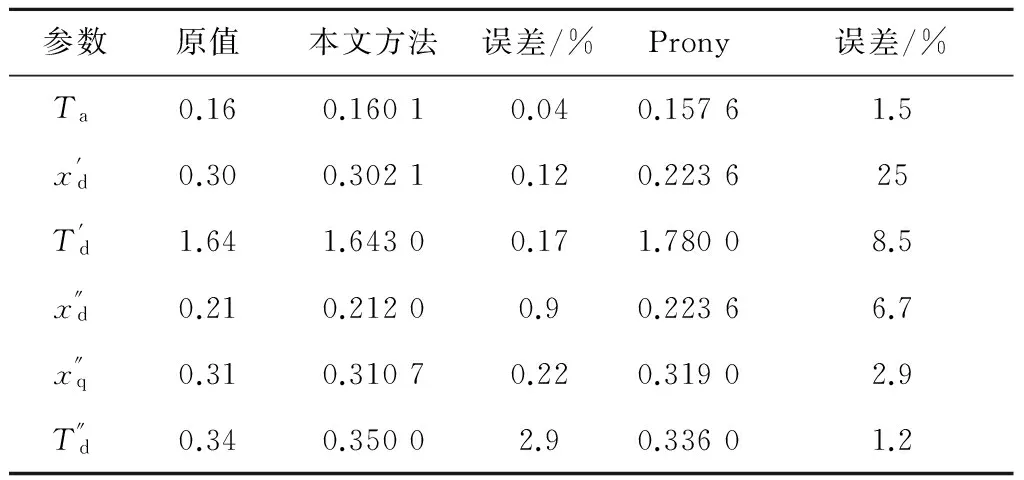
参数原值本文方法误差/%Prony误差/%Ta0.160.16010.040.15761.5x'd0.300.30210.120.223625T'd1.641.64300.171.78008.5x″d0.210.21200.90.22366.7x″q0.310.31070.220.31902.9T″d0.340.35002.90.33601.2

表3 不同信噪比下参数辨识结果Table 3 Identification results at different SNR

3.2 实验分析

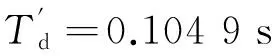
将辨识到的电机参数代入公式(18)，减去噪声部分e(t)，获得的实验电流与辨识电流如图4所示。经计算，两波形均方误差为0.06%，说明用本文方法提取电机参数是可行的。

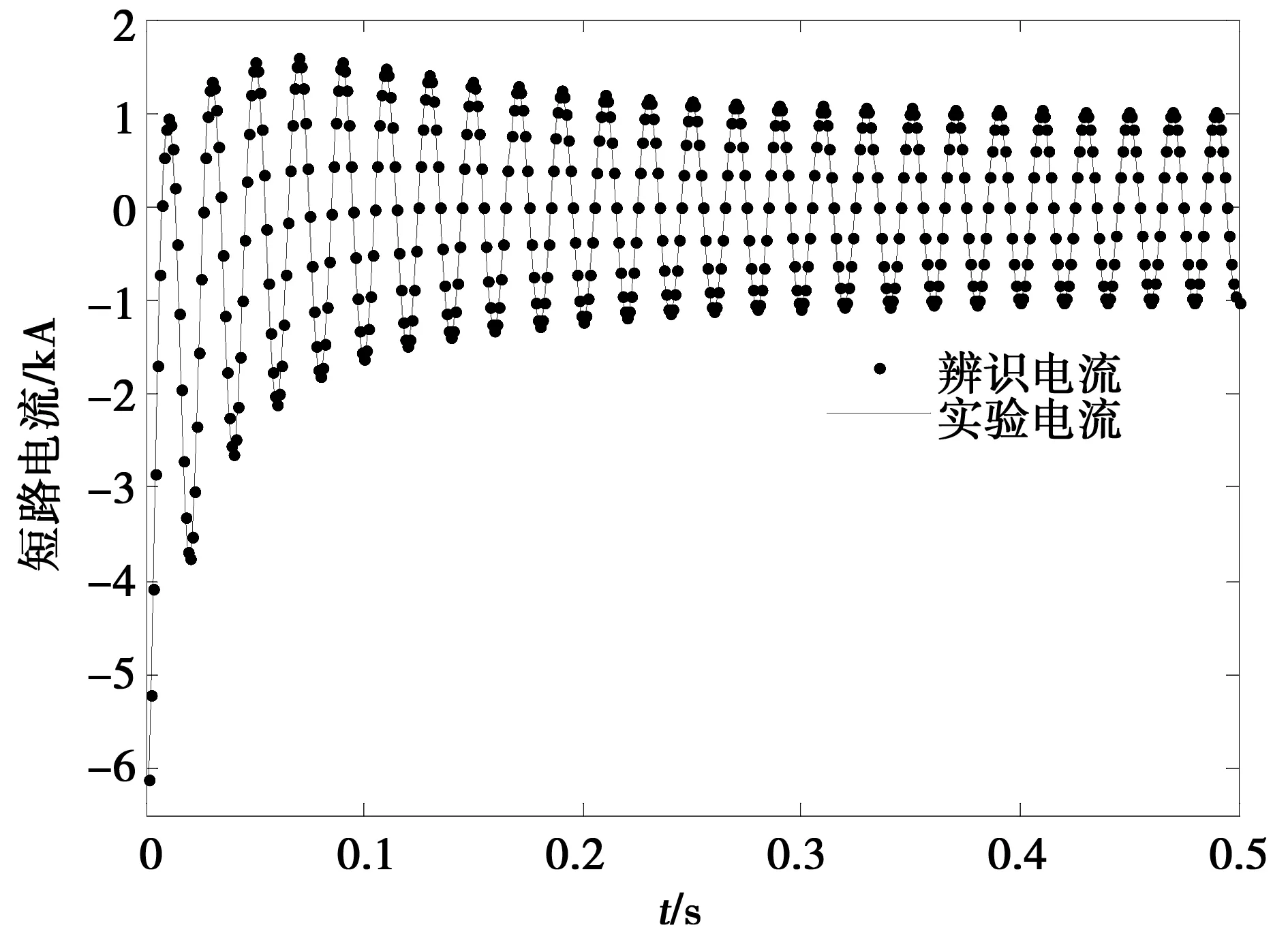
图4 辨识电流波形与实验电流波形Fig.4 Identifying current waveform and test current waveform

4 结 论

1)本文将EMD-SG与信息熵矩阵束算法有机结合对同步电机进行参数辨识，利用EMD对短路电流进行分解，采用SG平滑滤波去噪，跟阈值去噪相比，在噪声去除的同时也保证了高频信号细节部分的完整性。EMD分解与小波分解相比，也不存在选择小波基的问题，便于工程应用。

2)本文提出的算法和Prony算法相比，具有很强的抗噪能力，在信燥比低于30 dB时，得到的辨识精度明显高于Prony算法。

3)本文算法易于计算机实现，可操作性强。该算法为同步电机参数辨识提供了一条新思路，同时也为电力系统相关领域进行数据处理提供了一个新方法。

[1] 李天云,高磊,陈晓东,等.基于HHT的同步电机参数辨识[J].中国电机工程学报,2006，26(8): 153-158. LI Tianyun,GAO Lei,CHEN Xiaodong,et al.Parameter identification of synchronous machine based on HHT[J].Proceedings of the CSEE,2006,26(8):153-158.

[2] LIMA L.Dynamic Model Validation for Compliance with NERC Standards[C]// Proceedings of the 2009 IEEE Power & Energy Society General Meeting,July 26-30，2009,Schenectady,New York, USA.2009: 1-7.

[3] 李志强,汤涌,何凤军.基于时频变换的的同步电机参数辨识方法[J].中国电机工程学报,2014,34(19): 3202-3209. LI Zhiqiang,TANG Yong,HE Fengjun. A time-frequency transform based identification method for synchronous generator parameters [J].Proceedings of the CSEE,2014,34(19): 3202-3209.

[4] 陈振锋,钟彦儒,李洁.嵌入式永磁同步电机自适应在线参数辨识[J].电机与控制学报,2010,14(4): 9-13. CHEN Zhenfeng,ZHONG Yanru,LI Jie.Online adaptive parameter identification for interior permanent magnet synchronous motor drive[J]．Electric Machines and Control，2010，4(4): 9-13.

[5] 黄操,袁海文,马钊,等.基于Tikhonov正则化方法的同步电机参数辨识[J].电力系统自动化设备,2016,36(5): 107-111. HUANG Cao,YUAN Haiwen,Ma Zhao,et al.Synchronous generator parameter identification based on Tikhonov regularization method[J].Electric Power Automation Equipment,2016,36(5): 107-111.

[6] 吴旭升,马伟明,王公宝,等.基于小波和Prony的同步电机参数辨识[J].电力系统自动化,2003,27(19):38-42. WU Xusheng,MA Weiming,WANG Gongbao,et al.Parameter identification of synchronous machine based on wavelet transform and Prony algorithm[J].Automation of Electric Power Systems,2003, 27(19):38-42.

[7] 张宇辉,陈峰,李慧敏,等.基于小波变换和矩阵束算法的同步电机参数辨识[J].电力系统保护与控制，2012，40(9):87-92. ZHANG Yuhui,CHEN Feng,LI Huimin,et al.Parameter identification of synchronous machine based on wavelet transform and matrix pencil algorithm[J].Power System Protection and Control,2012,40(9):87-92.

[8] 李兴源,朱瑞可,王渝红,等.基于EMD和 Prony 算法的同步电机参数辨识[J].电网技术,2012,36(8):136-139． LI Xingyuan ZHU Ruike,WANG Yuhong,et al.Parameter identification of synchronous machine based on empirical mode decomposition and Prony algorithm[J].Power System Technology,2012,36(8):136-139.

[9] 李天云,祝磊,宋莉,等.基于TLS-ESPRIT的同步电机参数辨识[J].电工技术学报,2009,24(12):38-42. LI Tianyun,ZHU Lei,SONG Li,et al.Parameter Identification of synchronous machine based on TLS-ESPRIT[J].Transactions of China Electrotechnical Society,2009,24(12):38-42.

[10] 胡小丽,金明.基于EMD的图像信号去噪的改进方法[J].电子测量技术,2009,32(11):58-61. HU Xiaoli，JIN Ming．Improved algorithm of image signal denoising based on EMD[J].Electronic Measurement Technology，2009，32(11):58-61.

[11] 何正友,符玲,麦瑞坤,等.小波奇异熵及其在高压输电线路故障选相中的应用[J]．中国电机工程学报，2007,27(1): 31-36. HE Zhengyou,FU Ling,MAI Ruikun,et al．Study on wavelet singular entropy and its application to faulty phase selection in HV transmission lines[J].Proceedings of the CSEE,2007,27(1): 31-36.

[12] 李宽,李兴源,赵瑞,等.基于改进矩阵束的高压直流次同步振荡检测[J].电网技术,2012,36(4)：128-132. LI Kuan,LI Xingyuan,ZHAO Rui,et al.Detection of subsynchronous oscillation in HVDC transmission system based on improved matrix pencil method [J].Power System Technology,2012,36(4): 128-132.

[13] 赵礼杰.基于EMD的Prony算法在低频振荡模态参数辨识中的应用[J].电力系统保护与控制,2009,37(23):9-14. ZHAO Lijie.Application of Prony algorithm based on EMD for identifying model parameters of low-frequency oscillations[J].Power System Protection and Control,2009，37(23):9-14.

[14] 李天云,袁明哲,李军强,等.基于EMD和SSI的电力系统低频振荡模态参数识别方法[J].电力系统保护与控制,2011,39(8):6-10. LI Tianyun,YUAN Mingzhe,LI Junqiang,et al．Method of modal parameter identification of power system low frequency oscillation based on EMD and SSI[J]．Power System Protection and Control,2011,39(8):6-10.

[15] 李天云,袁明哲,李军强,等.基于EMD和SSI的电力系统低频振荡模态参数识别方法[J].电力系统保护与控制,2011,39(8): 6-10. LI Tianyun,YUAN Mingzhe,LI Junqiang,et al．Method of modalparameter identification of power system low frequency oscillation based on EMD and SSI[J].Power System Protection and Control,2011,39(8):6-10.

[16] HUANG N E,SHEN Z,LONG S R.The empirical mode decompositionand the Hilbert spectrum for nonlinear non-stationary time series analysis[J]．Proceedings of the Royal Society of London: Series A,1998(454): 903-995.

[17] 索南加乐,王莉,夏经德,等.特高压交流线路故障谐波分析[J].高电压技术,2010,36(1): 37-43． SUONAN Jiale,WANG Li,XIA Jingde,et al.Harmonic analysis of fault signal in UHV AC transmission line[J].High Voltage Engineering,2010,36(1): 37-43.

[18] 李天云,袁明哲,许广婷,等.基于随机子空间结合稳定图的间谐波高精度检测方法[J].电力系统自动化,2010,34(20): 50-54. LI Tianyun,YUAN Mingzhe,XU Guangting,et al.An inter-harmonics high-accuracy detection method based on stochastic subspace and stabilization diagram[J].Automation of Electric Power Systems,2010,34(20):50-54.

[19] 李天云,袁明哲,郑波,等.谐波和简谐波三参数识别的SSI-LS方法[J].电力系统保护与控制,2011,39(10):42-46. LI Tianyun,YUAN Mingzhe,ZHENG Bo,et al.A method of three parameters of harmonics andinter-harmonics high accuracy detection based on SSI-LS[J].Power System Protection and Control,2011,39(10): 42-46.

(编辑：刘素菊)

Parameter identification of synchronous generator based on EMD-SG and information entropy matrix pencil algorithm

GUO Xin-xin1， LU Hua-cai1， CHEN Ya-hui2， TIAN Li1

(1.Electrical Engineering School of Anhui Polytechnic University,Wuhu 241000,China;2.State Grid Henan Electric Power Company Hebi Power Supply Branch Company ,Hebi 458000,China)

In order to obtain accurate value of the generator parameters,especially transient and sub-transient parameters to satisfy the increasingly sophisticated simulation requirements of the power system,an empirical mode decomposition,savitzky-golay filtering and information entropy matrix pencil based method is proposed.It pretreated the short-circuit current by noise with the empirical mode decomposition to improve its signal to noise ratio.Then information entropy matrix pencil algorithm was used to extract the frequency and damping of each component of short-circuit current.Meanwhile,the transient parameters of synchronous generator were determined with higher accuracy by some simple calculations.Simulation and experiment results show that the proposed method has advantages of high parameter identification accuracy and strong anti-interference ability.

parameter identification; synchronous generator; empirical mode decomposition; information entropy; matrix pencil algorithm

2013-09-05

安徽省自然科学基金(1608085ME106)；安徽省高校科学基金重点项目(KJ2015A063)

郭欣欣(1980—)，女，硕士，副教授，研究方向为微电网及电力系统信号处理； 陆华才(1975—)，男，博士，教授，硕士生导师，研究方向为电机控制、电机优化设计； 陈亚辉(1987—)，男，硕士研究生，研究方向为电力系统调度自动化; 田 丽(1962—)，女，教授，硕士生导师，研究方向为复杂系统控制及参数辨识。

郭欣欣

10.15938/j.emc.2016.12.004

TM 341

:A

:1007-449X(2016)12-0025-07