能量法分析重力和点电荷双场联合作用下的微幅摆动
2017-01-06陈奎孚
陈奎孚 陈 雷 蔡 春
(1中国农业大学理学院,北京 100083; 2北京联合大学应用文理学院,北京 100191)

能量法分析重力和点电荷双场联合作用下的微幅摆动
陈奎孚1陈 雷1蔡 春2
(1中国农业大学理学院,北京 100083;2北京联合大学应用文理学院,北京 100191)
单摆是经典的教学案例.为了丰富教学材料,文章分析了点电荷场和重力场联合作用下的摆动.采用了适合于单自由度的自然坐标系描述系统,使用了适合于复杂力学的能量法建立动力学方程.针对固定点电荷处于摆悬挂点垂线的特殊情形,通过理论分析界定了摆球最低、倒立和倾斜等平衡位置的参数范围.
摆;点电荷;振动;能量法;自然坐标系
单摆在中学物理和大学物理中都是一个典型物理教学案例[1].最简单的模型是没有重量且没有弹性的细绳悬挂大小不计的摆球在重力场中微幅摆动.为了丰富教学内容和增强学习兴趣,很多教学材料又对最简单的模型进行了拓展,如加速悬挂点、放置斜面、增加均匀电场力等.很多拓展模型的求解只需对基本模型的解进行简单修正就可以了,这是因为在这些例题中,拓展的作用仅相当于增加了一个均匀的力场.
点电荷场是物理教学的基本内容,但是由于场强的不均匀性,将它与重力场联合作用于摆所引起的物理现象就复杂了,仅就其平衡位置而言,除了常规的摆球最低情形外,还有倒立和倾斜等情形.文献[2]仅就摆球最低这一常规平衡位置情形进行了详尽的研究,本文则利用能量法[3]进行更为一般的讨论,并就固定点电荷处于摆悬挂点垂线上的特例,给出所有稳定平衡位置的参数取值范围.
1 能量法[3]
摆的自由度只有一个,质点的运动轨迹是已知的,所以可选择沿质点轨迹的弧坐标s为广义坐标.相应地,质点动能Ek可简洁地表示为

图1 两个点电荷相互作用的势能分析
(1)
记系统势能为Ep,它等于各势能的代数累加.势能是位置的函数,质点的位置由其弧坐标s唯一确定,所以Ep是s的函数Ep(s).
对无阻尼情形,动能与势能之和总能量E守恒,即不随时间而变.数学语言表示为
(2)
两边对时间求导有

(3)
假定系统能够发生微幅简谐振动,记系统平衡位置s=sb.对于微幅振动,可把Ep(s)展开成s-sb的泰勒级数,即
(4)
代入式(3)得到
(5)

(6)
如果在分析一开始就找到平衡位置,并且设平衡位置的sb=0,则式(6)变成如下简洁的形式
(7)
式(6)为线性微幅振动微分方程.对应物理系统的固有频率为
(8)
或振动固有周期为
(9)
从式(6)(或式(8))可以看出,线性微幅振动分析的关键是找到E″p(sb).与弹簧振子的微分方程相比,式(7)的E″p(0)相当于弹簧的劲度系数.稳定平衡则要求E″p(sb)>0;而E″p(sb)<0则为不稳定平衡(系统无法发生“围绕”不稳定平衡位置的往复运动);E″p(sb)=0为临界情形,系统能否发生围绕s=sb振动,需要检查更高级导数的正负.
2 两个点电荷相互作用的势能分析
运用式(6)的关键是写系统势能,先看图1(a)所示两个点电荷相互作用的势能,图中O处点电荷固定(Q),移动点电荷q沿轨迹运动.选择O′为零势能点,则电荷A的电势能为
(10)
式中,k=9×109N·m2/C2为静电力常量.将Ee(s)对s求导有
(11)
(12)

(13)
将式(13)代入式(12)得到
(14)
将式(14)代入式(11)得到
(15)
对式(15)再次求导有
(16)

(17)

从该式解出βA-β=Δθ-Δφ,代入式(17)有
(18)
考察图1(b)可知,Δssinβ≈BC≈rΔθ,因此式(18)中的
(19)
图1中的固定电荷和质点轨迹的曲率中心在轨迹的同侧.对于二者在曲线两侧的情形,同样可证式(19)仍然成立.将式(14),式(18),式(19)代入式(16)得到
(20)

3 电荷场与重力场联合作用
考查图2所示的联合作用情形.直角坐标系原点过单摆的悬挂点H.固定点电荷Q位于 O(a,b).摆长l, 摆球是质量为m质点,带有电荷q.自然坐标原点取为摆球的最低点,正方向如图2所示.重力势能和电势能的零点均选择自然坐标原点.
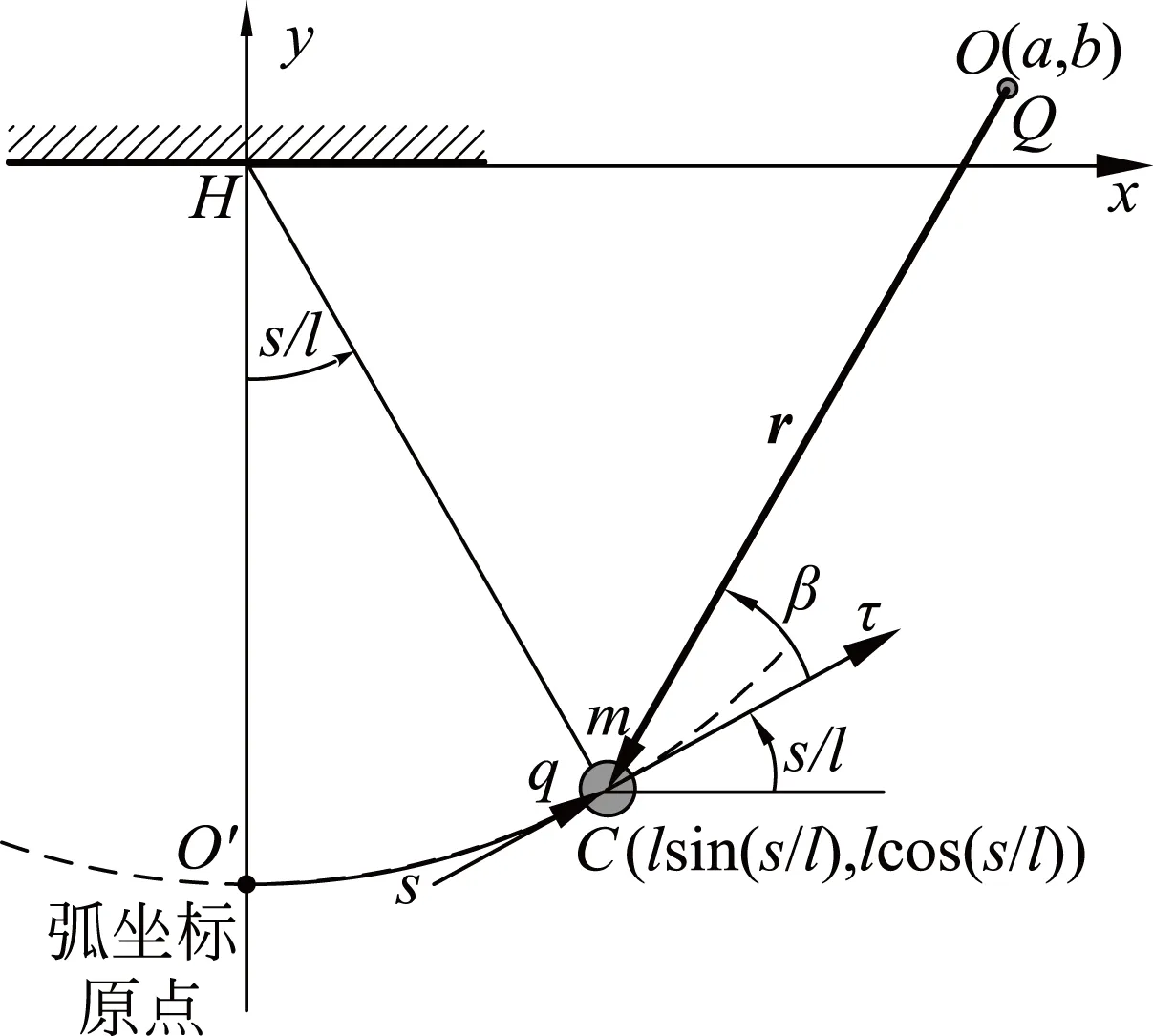
图2 点电荷场与重力场联合作用
重力势能为
它对弧长的一阶和二阶导数分别为
系统的势能为
(21)

(22)
其中
(23)
(24)
式(22),式(23)和式(24)看起来很复杂,但它们只是关于单变量sb的方程.一旦a,b,l,q,Q给定,就可以通过数值方法确定出sb.确定出sb后,可用它作新自然坐标的原点,就得到式(7)那样微幅简谐振动方程了.
等效刚度E″p(sb)则为
(25)
固有频率和简谐振动周期分别按式(7)和式(8)确定.
为了便于分析,引入如下无量纲参数
则式(22)~ (25)可分别写成
(26)
(27)
(28)
(29)
4 特例考察
本文只考察固定电荷Q位于y轴的特殊情形,相应的a=0.式(28)的余弦变成
(30)
代入式(26)得到
(31)
解方程(31)得到平衡位置
(32)
(33)
(34)
4.1 常规稳定平衡
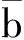
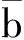
E″p(θb)>0要求
(35)
此时s=sb=0为稳定平衡位置,对应的振动周期为
(36)
若采用与文献[1]相同的符号,则式(36)就是该文的式(2).


图3 平衡位置类型分析
(37)
稳定平衡E″p(θb)的要求为
(38)
当式(39)得到满足时,系统的固有周期为
(39)
若采用与文献(1)相同的符号,则式(39)就是该文的式(4).
4.2 倒立稳定平衡
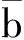
(40)
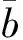
(41)
4.3 倾斜稳定平衡
式(33)的右边必须大于零,所以有μ<0.该条件得到满足后,从式(34)可解得
(42)
若式(42)的解存在,则正负各有一个.但是解的存在还要补充其他条件.根据三角函数的性质有
(43)
进一步化简得到
(44)
(45)
稳定平衡E″p(θb)的要求为
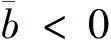
(46)
相应地,式(44)的关系也就能更进一步明确为
(47)
这类稳定平衡是靠位于摆悬挂点下方的同性电荷的斥力来维持的.
三类稳定平衡的参数范围如图4所示.由图可知倾斜平衡和常规平衡是互斥的,即同一组参数不可能既有常规平衡,又有倾斜平衡.同样倒立平衡和倾斜平衡也是互斥的.但是常规平衡和倒立平衡却是可以同时存在的.

图4 三类稳定平衡的参数范围
5 微幅振动讨论
由式(6)只要保证E″p(θb)>0,系统就会围绕平衡位置发生微幅简谐振动,而不管点电荷位于何处,只是当点电荷处于摆的悬挂点的垂线上时,分析过程比较简单一点,正如第4节所述.当然点电荷不在摆的悬挂点的垂线上,那么平衡的θb一般不再为零,但是仍然可以通过式(26)~(29)来确定,并且是绕θb的简谐振动.因此对“点电荷场与重力场叠加时的方向关系是带电单摆保持简谐运动的首要因素”的说法不能苟同.
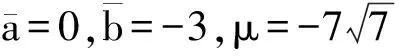
是不是所有微幅振动都是简谐的呢?从式(6)来看,这似乎是肯定的,但是E″p(sb)=0则为例外情况,图5(a)就是这样的物理模型.图中振动系统位于光滑的水平面,振动沿弹簧轴线的垂直方向运动,过平衡位置弹簧无伸长.这个模型因E″p(sb)=0,所发生振动即使很微小,也不能用简谐振动来近似.

图5 非简谐微幅振动
式(6)的操作默认了势能函数二阶可微.但是也有Ep(s)的二阶导数不存在的模型,比如图5(b)所示的在对称光滑V形槽内质点的运动,其重力势能Ep(s)=|s|sinθ)就没有二阶导数.虽然质点可以在V形槽内往复运动,但即使幅度再小,也不符合简谐规律.
6 结语
本文研究了在重力场和点电荷场共同作用下的摆.由于系统为单自由度系统,摆球的轨迹已知,所以采用了自然法描述系统.又因为所研究的系统相对复杂,故采用能量法建立振动微分方程,
它的操作过程比受力分析法要简洁一些.
因为采用的是自然坐标系,所以本文推导了矢径长度对自然坐标的导数和轨迹到矢径的角度对自然坐标的导数.这两个导数是进行相关研究的数学基础.
针对点电荷位于摆悬挂点铅垂线上的情形,经由理论分析得出它具有常规、倒立和倾斜三类稳定的平衡位置.给出了3类稳定平衡的参数范围.
对微幅振动和简谐振动的概念进行了辨析.
[1] 梁绍荣,刘昌华,盛正华.普通物理学[M].北京:高等教育出版社,1999:233-235.
[2] 唐安琪,陈钢,朱国斌,等.点电荷场中的重力单摆及简谐振动[J].物理与工程,2015,25(3):79-83.TangAQ,ChenG,ZhuGB,etal.GravityPendulumandHarmonicVibrationintheFieldofPointCharge[J].PhysicsandEngineering, 2015, 25(3): 79-83.
[3] 陈奎孚.机械振动基础[M].北京:中国农业大学出版社,2011:29-31.
■
ON THE MICRO-AMPLITUDE VIBRATION OF A PENDULUM IN THE SIMULTANEOUS FIELD OF THE GRAVITY AND POINT CHARGE BY THE ENERGY METHOD
Chen Kuifu1Chen Lei1Cai Chun2
(1College of Science, China Agricultural University, Beijing 100083;2College of Arts and Science, Beijing Union University, Beijing 100191)
The simple pendulum is a typical teaching case. To enrich teaching materials, we studied the micro-amplitude pendulum vibration caused by the simultaneous point charge and gravity fields. The system is described by the natural coordinate system, which is apt to the single-degree-of-freedom case investigated here. The dynamics equation is evolved from the energy method, which is more concise than the free-body-diagram method for the complex system in this study. After a general analysis, we focus on a particular case wherein the point charge is at the vertical line passing through the pendulum suspension point. Theoretical analysis indicates that this particular case is characterized with three types of stable balance. The three types are the ordinary, the inverted and the oblique distinguished by the pendulum rope’s inclination. Their parametric domains are delimited.
pendulum; point charge; vibration; energy method; natural coordinate system
2015-09-08;
2016-03-03
北京市属高等学校高层次人才引进与培养计划项目(CIT&TCD201404080).
陈雷,男,硕士研究生,力学专业.
蔡春,女,教授,主要从事数学科研和教学工作.caichun@buu.edu.cn
陈奎孚,陈雷,蔡春. 能量法分析重力和点电荷双场联合作用下的微幅摆动[J]. 物理与工程,2016,26(6):25-30.
