解析2016年诺贝尔物理学奖
2017-01-06张广铭
张广铭
(清华大学物理系,北京 100084)
特约稿件
解析2016年诺贝尔物理学奖
张广铭
(清华大学物理系,北京 100084)
北京时间2016年10月4日下午5点45分,本年度诺贝尔物理学奖揭晓:3位理论物理学家——美国华盛顿大学的David J.Thouless(戴维·索利斯)、普林斯顿大学的F.Duncan M.Haldane(邓肯·霍尔丹)和布朗大学的J. Michael Kosterlitz(迈克尔·科斯特利茨)获奖,以表彰他们在理论上提出物质的拓扑相变和拓扑相.本刊编辑当晚与清华大学物理系张广铭教授电话联系采访.期刊主编王青教授拟写了采访提纲,经过商量,王青老师和编辑部钱飒飒、刘洋一行3人在张教授办公室展开了下面的问答.
王青: 《物理与工程》是教育部大学物理教学指导委员会会刊,读者主要是全国教和学大学物理的老师和学生.每年期刊都有一篇介绍年度诺贝尔物理学奖的文章,希望张老师的讲解能让广大的物理教师听懂并且能采用到他们的课堂中.
张广铭: 我前一段时间应文小刚老师之邀,在“赛先生”发表了一篇文章《物理诺奖之Haldane相的来龙去脉》,介绍了Haldane教授部分获奖工作.
王青: 今年的物理诺奖研究涉及凝聚态理论,还是很专业的.我自己不做这行,为了了解内容先下载了两份诺奖官网资料,一个是公众性的介绍“Popular Science Background ”,一个是更专业一些的介绍 “Advanced Scientific Background on the Nobel Prize in Physics 2016”,以此为目标起草采访提纲.希望这篇采访文章能通过期刊平台让教大学物理的老师们能看明白,促使他们能把相关内容变成自己的语言在课堂上传递给学生,因此希望张广铭老师尽量讲得通俗一些,把最前沿的物理进展通过这样的方式教授给上大学物理的学生,进而传播给社会.
张广铭: 我在清华物理系上了两门课,一门是本科高年级的统计物理2,一门是研究生的量子多体理论.正好(提纲中)这些问题上课都有所涵盖,还算熟悉.我上课时就力求用浅显的语言给出图像化描述,有可能达到你说的(通俗)目标.
1 关于物质的相
王青: 今年诺奖工作中涉及的物理概念是物质的相、相变及拓扑在其中的作用.首先,什么是物质的相?相和物态是一回事吗?
张广铭: 在说物质的相之前,先说物态.其实物态是比较简单的,物质的形态就是气、液、固,加上等离子体,简称物态.至于相就是对每一种物态再进行了细分分成了若干不同的相,相可以有很多种,但是物态却只有4种.
王青: 可以用对称性自发破缺的不同方式来描写和分类物质的不同的相? 是不是像液相到固相转变时,对称性从连续的变到分离的,或小磁矩空间指向随机排列到沿同方向排列那样的破缺来分类的吗?
张广铭: 基本上是这样的.刚才说到了物态,物态下面又分不同的相,那么不同的相是怎么来刻画呢?就是根据它们各自所具有的对称性来刻画.比如液态到固态,从相的角度这两个相就具有不同的对称性,液态具有连续的平移不变性,固态就不再具有平移不变性了,而是有周期性的结构了.比如日常生活中固态的水有很多相,冰、霜、雪花等不下于10种.就拿雪花的结构来说它又有8种以上不同的晶体结构(见下图).因此,相的概念就更加准确地描述了物态,因为不同结构的雪花有不同的空间对称性,它们都是水分子形成的固态.

雪花的晶体结构
再比如磁性材料,当升高温度到所谓的居里温度以上时就变成非磁的了,这种非磁性我们叫做顺磁态.从顺磁态到有磁性的铁磁态有什么不同?就是固体当中每个原子的磁矩空间指向发生了变化,在顺磁态的时候它的空间指向是任意的,所以它有磁矩空间连续旋转的不变性.但是到了铁磁态的时候,多数原子空间指向趋向某一个方向,这个时候,它的原子磁性空间旋转对称性发生了破缺,就不再有连续旋转对称性了,它就是一个新的相——铁磁相.
王青: 从一个相到另一个相,对称性是在变化的,破缺是变大了还是变小了,还是都是有可能的?
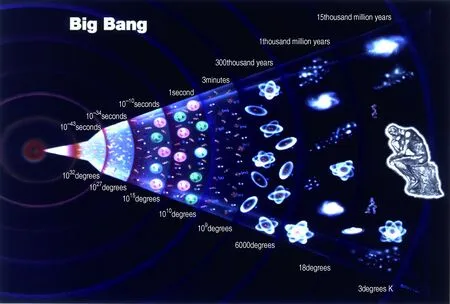
宇宙大爆炸
张广铭: 我们通常描述相变的时候都是从简单到复杂,也就是说,当在很高温度的时候,所有的物态都变成等离子体态,随着降低温度就慢慢形成原子、分子,然后到气体、液体、固体,所以随着温度和能量的降低,物质的形态会从原来简单的状态变成越来越复杂的状态.这样一个过程对应的就是一个对称性破缺的过程,这是通用的一个过程,如下面的宇宙大爆炸示意图.当然反过来也是成立的,就是从一个复杂的状态慢慢变成一个简单的状态.用对称性对各种相进行描述,构成了所谓朗道理论,并成为凝聚态物理学的奠基石.所以上面提到的用对称性破缺来描写和分类各种物质形态在凝聚态物理学中是非常重要的内容,朗道理论描述的各种物相、序参量、低能激发等详见表1.

表1 具有对称破缺现象特征的凝聚态物质系统
王青: 那些不能用对称性自发破缺描写和分类的物质相又有什么独有的特点?拓扑在这类相中起什么样的作用?什么是拓扑相?
张广铭: 今年的3位诺贝尔物理学奖获得者,在理论上发现存在另外一些不能用朗道范式来描述的相和相变,因此他们的工作非常重要.朗道范式是用对称性破缺来描述相和相变,很重要的物理量就是局域的序参量,这个序参量是实验可直接测量的.比如从顺磁到铁磁的转变,这个序参量就是磁化强度.磁化强度是实验可以直接测量的,朗道理论能描述的相变都是存在这样的序参量,所以有了序参量我们就可以描述相和相变.对于拓扑相和拓扑相变就不存在这样的序参量,所以我们需要找到新的办法来研究这些相与相变.
对于一个没有序参量能描述的物相,怎么去刻画它呢?人们发现数学中的拓扑概念,在这里面有很大的帮助.因为这类相都有一个特点就像一个不可压缩的物体一样,当受到外界压缩时,它只能变形,体积是不会改变的.
什么叫拓扑?就是你把一个系统进行形变的时候,还有某些物理量保持不变,保持不变的物理量就是拓扑不变量.物理上讲的拓扑态都有这样的特征,体是不可压缩的,所以看到的物理现象全都体现在它的边缘上.因为当一个不可压缩的东西形变时,发生改变的就是在边缘上,从边缘态的行为就可以决定整个系统的性质,这种边缘与体的对应关系,也称为全息定理.从系统边界上态的性质就能反映出整个体的性质,这正是拓扑概念的体现.
王青: 请给我们解释一下什么叫无序相,什么叫有序相.
张广铭: 无序相它具有各种各样的对称性,连续平移不变性,连续旋转不变性等等,就像气态.若它们变成固体的话,原子的排布就变成有一定结构了成为有序相.
王青: 拓扑相是不是人们看到唯一的超出朗道范式的相?
张广铭: 目前可以这么说.今年的3位诺贝尔物理学奖获得者就是在一些原来被人们认为没有结构、没有对称性破缺的无序相里,发现了新的结构,它们不是完全的无序,而是有某种特殊的量子有序或隐藏序.
王青: 你刚才提到量子序,一定是量子的对不对?如果抛开量子就没有这样的序或者相,对吗?
张广铭: 可以这么讲.
王青: 这样的相能够体现出宏观量子效应吗?
张广铭: 有的有,有的没有.
王青: 因为通常量子效应是非常小的,如果能宏观看到应该是一个很特别的性状或特点.
张广铭: 这些相通常是在极低温、强磁场的条件下才能够实现,并且需要极其精密的测量才能发现,在我们日常室温或常压下是无法实现的.
王青: 怎么能看出偶的磁矩链是非拓扑的,而奇的磁矩链是拓扑的?
张广铭: 这个问题在诺奖的官网材料里没有讲清楚或者说讲错了.从量子力学角度看,原子都带有磁矩,因为原子的外面有电子,电子围绕原子核的运动以及电子本身还有磁矩,所以整个原子是有磁矩的.磁矩的大小根据量子力学原理可以取半整数或者整数,不同的原子具有不同大小的磁矩.当它们形成一维链状的材料就表现出不同的物理性质.它们的性质首先取决于单个原子磁矩的大小,是半整数还是整数.如果是半整数(半整数是不能被整除的),这种原子所形成的一维反铁磁链,它的低能激发是没有能隙的,众多的原子磁矩会形成像水波一样的自旋波.今年获得诺贝尔奖的Haldane在1983年提出一个重要的猜想,认为所有整数自旋链的低能激发都是有能隙的,因此它们不能形成像水波一样的自旋波.做个比喻,半整数自旋链就有点像固体当中的金属一样,激发无能隙,而整数自旋链的性质有点像绝缘体,激发有能隙.
在2009年,随着拓扑量子物态研究的展开,物理学家发现在整数反铁磁自旋链当中的偶整数磁性链的基态没有拓扑性,只有奇整数自旋链的基态具有拓扑性.这就像在普通的绝缘体当中人们进一步分出了拓扑绝缘体与能带绝缘体一样.
为什么偶整数磁性链是非拓扑的,奇整数是拓扑的.我们是要看它的边缘激发的性质.整数磁性链边界上的磁矩都会分化,变成一半的原子磁距大小.偶整数链在边界上变成一半还是个整数,奇整数链在边界上磁矩变成了半整数,所以它们分别对应不同的状态.因此,偶整数磁性链和奇整数磁性链,它们在边界上自由的磁矩是不一样的.我们从量子力学中知道,具有半整数自旋的粒子都具有不平凡的性质,因为一个自旋1/2的粒子旋转360°,它的波函数会有一个“π”的位相改变;而对一个自旋为1的粒子,就没有这个改变.
王青: 刚才你说到边界上磁矩变成一半了,能给我们详细解释一下吗?
张广铭: 有一个简单图像,可以帮助理解为什么整数自旋链是有能隙的和边界上原子磁矩为一半.你可以把每个原子磁矩看成由两个一半的磁矩所形成的一个对称化的束缚多重态,同时半个磁矩与近邻格点上半个磁矩形成一个束缚单态.这样,整数自旋链可以形成一个有能隙的量子多体基态,但在边界上存在半个近自由的磁矩.这个量子多体基态是否为拓扑量子态,就取决于边界上这个近自由的磁矩是否为半整数.见下图所示.

边界上原子磁矩为一半
2 关于物质的相变
王青: 刚才你提到朗道理论里面相变是用序参量来描写的,也提到了是一个局域的序参量.请介绍一下什么是序参量?它有什么物理图像吗?
张广铭: 序参量实际上是一个可观测的物理量,它是描述物态或者相有序的物理量.比如从顺磁态到铁磁态的相变当中,描述铁磁有序的序参量就是磁化强度.
王青 : 这个物理量取不同的值表示不同的相,还是只能取零和非零.
张广铭: 零和非零.
王青: 非零时,取不同的值是同一个相?
张广铭: 是同一个相.
王青: 它的图像呢?
张广铭: 比如从顺磁到铁磁的磁化强度,磁化强度就是把每一个原子的磁距大小做平均.所以它的物理图像就是描述原子磁距的空间指向是随机的还是限制在某一个方向上.如果是完全随机的,那就对应无序相,它的期待值就等于零.如果倾向于某一个方向,它的平均值就是有确定方向的非零值了.
王青: 前面你强调一定是一个局域的,有没有是非局域的序参量.
张广铭: 所有朗道理论能描述的相与相变都要求存在局域的序参量,因为只有局域的序参量才是实验可以直接测量的,用它才能建立朗道相变理论,所以这些序参量必须是局域的.而非局域的序参量是实验不能直接测量的东西,所以不能用来描述无序到有序的相变.
3 拓扑概念在相与相变中的作用
王青: 用序参量描写的相变和不能用序参量描写的相变的异和同,拓扑在里面起什么作用?
张广铭: 用序参量描写的相变本质上刻画的是无序到有序的变化,而不能用序参量描写的相变,有一类从理论上可以找到所谓的非局域序参量或拓扑序参量来描述.非局域的序参量所描述的现象,实际上是一种所谓的隐藏序,更本质上讲,背后还是某种拓扑性质.
王青: 我理解你的拓扑在理论上描述是用所谓的拓扑荷,它起的作用是不是和序参数是一样的?
张广铭: 拓扑荷是不能连续变化的,所以不能用于描述相变.
王青: 什么是拓扑缺陷?因为在诺贝尔奖里面特别提到了它,也提到它在二维体系的相变中起非常重要的作用,你能给我们解释一下吗?
张广铭: 当然拓扑缺陷有很多.拓扑缺陷实际上在我们日常生活中都可以观察到,一个洗脸的水池当你灌满水之后再把水放掉,水会形成一个涡旋.还有台风也是一种移动的涡旋,涡旋就是一种拓扑缺陷.
王青: 从字面上怎么理解涡旋是一种拓扑缺陷呢?
张广铭: 如果有涡旋,绕涡旋走一圈的话,描述涡旋的函数会有一个2π的相位改变.
王青: 我想象的是缺陷总是少了哪一块东西,你现在说是转一圈回来它不会回到原样,有一些新的东西出现?
张广铭: 通常情况下,这种激发它会来回跑动的,当有一个杂质或者位错的时候,它会把这个涡旋固定住,就像水池下面出水口的塞子,但是台风的涡旋是会跑的.
王青: 你的意思就是固定在那儿的就叫缺陷?
张广铭: 如果那里有一个缺陷就会把这种涡旋固定在那里.
王青: 所以通过这个东西可以看到哪块有一个缺陷.那你说随便跑的那种就不叫拓扑缺陷?
张广铭: 那叫拓扑涡旋.通常要想产生一对拓扑涡旋,需要很大的能量,但是在二维体系中产生一对涡旋对的话,所需要的能量是有限的,这跟在三维是不一样的.因此,拓扑涡旋在二维就会导致特殊的物理效应.
王青: 什么是KT相变,它和其他相变有什么相同和不同之处?说它是普适的是什么意思?为什么说它是20世纪凝聚态物理理论最重要的发现?
张广铭: Kosterlitz-Thouless(KT)相变,是指在二维体系当中从一个涡旋配对的状态到涡旋自由的状态转变过程,它是由温度引起.因为涡旋分为两种,一种是正涡旋,另一种是反涡旋,如下图所示。高温情况下,二维体系中产生的涡旋正、反都有,它们是互相独立的,但是到了低温,正涡旋和反涡旋配对形成稳定的结构,进入一个新的相.从这个图像上看,KT相变也是一种高温无序到低温有序的相变.由于是在二维体系,有序相不是真正的长程有序,而是准长程有序,关联函数呈幂函数形式.

正涡旋和反涡旋
KT相变与其他的相变有什么不同呢?首先从热力学量来看,在相变过程中所有热力学量没有明显的改变;再有一个不同就是没有局域序参量来描述这个相变.KT相变可以用拓扑序参量完整地进行描述.
为什么说它是普适的?关于一个相变的普适性在理论上已有很多研究了.普适性是指这个相变本质,因为在我们自然界中存在很多相变,表面上看很多相的话就会有很多很多的相变,但实际情况不是这样.你会发现有些完全不相关的不同体系,它所发生相变从物理本质来讲是类似的.比如,从顺磁到铁磁相的转变和气体到液体在临界点的转变,相变时系统所表示出的奇异的行为是完全一样的,那就表明这两个不同体系它发生相变的原因和背后的物理是相同的,所以我们就把很多这种表面上看不同的相变进行了分类.分类之后,我们会发现相变的种类是有限的,是什么决定相变的类型呢?有两个参数:一个是系统的空间维数,另外就是序参量的维数.比如,从顺磁到铁磁的相变,如果磁体是三维的,那么空间维数等于3,那么它的序参量是几维的?如果它是一个矢量,那么它的维数就是3,这两个刻画系统相变的参数就决定了相变是属于哪一类的.
KT相变虽然说是拓扑的相变,但由于它描述的还是一个经典系统,可以用拓扑的序参数来描述这个相变.从某种意义上来说,它还不是远离朗道的理论,只不过是它的序参数是一个拓扑量而不是一个实验直接测量的量.它的空间维数是2,它的拓扑序参量也是2,这两个量就决定了一个相变的类.所有的空间维数是2,序参量维数是2的相变都和KT相变属同一个类.
为什么说它是20世纪凝聚态物理最重要的发现呢?因为在它之前物理学家普遍认为在二维体系不存在相变,这是有严格的数学证明的,但是这个证明忽略了拓扑激发的存在.因此他们的发现突破了前面所有的限制,把拓扑的概念引入到物理当中;这个KT相变本身又超越了朗道的相与相变的理论范式;它开辟了后面若干年凝聚态物理学发展的方向,因此,我们现在说它是20世纪凝聚态物理理论最重要的发现是基于以上3点原因.
王青: 什么是涡旋和涡旋的激发?
张广铭: 如果原子的磁矩被限制在一个平面内的话,它的磁矩指向只能在那个平面内,所以平面内原子磁矩的描述就可以用一个方位角来刻画它.对于磁矩限定在二维的磁性薄膜上的情形,它就较容易形成涡旋的激发,就是看它磁矩的指向,绕涡旋走一圈磁距的指向正好转了一个2π,所以就产生一个涡旋.
王青: 你讲的涡旋我能理解,但是怎么能看出它激发了?
张广铭: 这种涡旋的产生是有一定条件的,它是能量较高的状态,它不是作为基态出现的.
王青: 你说涡旋本身的存在就是一个激发了?
张广铭: 对.
王青: 它的拓扑性质如何体现?它在物理中起什么作用?
张广铭: 在二维空间,正、反两个涡旋如果形成对的话,需要的能量是有限的,同时产生单个涡旋需要很大的能量.涡旋作为一个激发在很多系统中都会出现,刚才说的是磁性系统,实际上不一定是磁性系统.假如一个相变的有序相是用一个复变函数描述的话,复变函数它有模和相位,它的相位本身就跟局限在平面上磁矩的相位是同样的,所以在很多物理系统中这种涡旋激发的产生都会出现.
王青: 能否通俗地解释一下拓扑是如何导致霍尔电导量子化的?
张广铭: 量子霍尔效应产生在所谓的半导体异质结中,就是有两种不同的半导体材料放在一起形成一个界面,当中电子就会被束缚在这个界面上,所以电子就会在这个平面内运动.当外加一个垂直于这个界面的磁场,电子会在这个磁场内做回旋运动,所以平面内的电子就不能走直线运动而改为在原地打转,因此它的体内就像是一个绝缘体一样不会导电.但是如果考虑位于边界上的电子的话,边界上的电子只能在体内转半圈,然后从一个位置偏到另一个位置,所以霍尔电导的产生来源于边界上电子的定向运动.见下图.

由于磁场的大小决定电子回旋半径的大小,所以在给定磁场的情况下,电子回旋是有一定的量子轨道,每个轨道上电子的能量是离散的.当磁场的大小使得一个单位磁通里只有一个电子的时候,边界上就只有一个导电通道,所产生的电导就是e2/h.体系的霍尔电导取决于边界上有多少个导电的通道,所以霍尔电导取值是量子化的.在实验上,观测到整数量子霍尔效应要在温度2K和15T的磁场下(磁场很强温度很低)才行.
Thouless和他的合作者,在1982年证明平面内的二维电子气在强磁场下,用量子力学可以计算这个系统的霍尔电导,发现这个霍尔电导和数学上的拓扑陈数是等价的.拓扑量子数就是刻画这个系统边界上有多少完美的导电通道数或边界.假如一个平面中间没有空洞的话,体系的边界只是外面一侧,如果中间挖掉一块的话那么这个系统就会产生另外一个边界.在这个边界上也会有无阻的电子定向运动,所以霍尔电导就会发生整数倍量子电导的改变.所以霍尔电导所对应的陈数就是刻画你这个系统有多少个空洞,它是拓扑量子数.
实现量子化的霍尔电导需要接近绝对零温和强磁场才能实现,所以实现起来非常困难.大家就想有没有不需要极低温和强磁场也能实现?那么就需要找一种特殊的材料系统,虽然没有一个外加强磁场的作用,但是这些固体材料中会有内部磁场.比如,对没有磁性的材料中加入一些磁性杂质就会使得材料的内部产生磁场,1988年邓肯.Haldane就提出对一种特殊的二维结构,可以通过产生内部的磁场来实现整数量子霍尔效应.
王青: 实际上就是说,真正在系统里面存在有效的磁场?
张广铭: 来自系统内部.
王青: 拓扑在绝缘体的分类中起什么样的作用?
张广铭: 在拓扑的概念被引进物相分类之前,所对应的态都属于无序态,把拓扑概念引进来之后我们就可以进行更进一步的分类.有些具有所谓拓扑序,有些没有.从量子的角度来看物质内部结构的特征,比如能带结构是不是有反转这些现象,反转是不是受到对称性的保护,所以我们才有“对称保护拓扑态”的提出,比如拓扑绝缘体就是受到时间反演对称保护的拓扑物态.而有些是不需要对称保护的拓扑物态,如量子霍尔效应.拓扑帮助我们对原来无序的相做了进一步的分类,进一步提高了认识.你可以知道它有很多内部的结构,这些结构是一些量子性的结构不是经典的东西.目前大家又有一个新的认识,就是认为量子纠缠也是一个重要的概念,可以帮助我们刻画一个系统的拓扑性质.只有量子系统才具有量子纠缠的性质,而经典系统是不存在量子纠缠的.
王青: 这个我一直有点混淆,拓扑和纠缠是两个不相干的事情.
张广铭: 人们近年发现有些物态它具有的拓扑性质从现有描述的方法看好像是相同的,但是发现它们之间存在相变,表明它们是不同的相.它们的本质是什么呢?这些例子促使人们意识到仅仅用拓扑这个概念来描述所谓的拓扑量子物态可能还是不够充分,所以认为可能的一个重要概念就是量子纠缠,这方面已经有很大的发展.
王青: 拓扑里面一定有纠缠还是纠缠里面一定有拓扑?还是拓扑里面可以没纠缠,纠缠里面可以没拓扑?
张广铭: 拓扑量子物态中一定有某种形式的量子纠缠,反过来量子纠缠中有没有拓扑就要做具体分析.
王青: 因为纠缠是一个纯量子力学里的概念,拓扑是一个数学上的概念,所以怎么说这两个也连不到一起.从拓扑的角度把物态或物质的相分成很重要的两类:一类是有拓扑的,另一类是没有拓扑的.
张广铭: 我刚才的意思就是目前的研究表明,拓扑物态里面可能还有进一步的微观结构.人们对物态、物相的认识,特别是量子拓扑物态的认识实际上还非常粗浅,今后还会有很大的发展.
4 关于超流和超导
王青: 什么是超流?超流和超导的区别和联系是什么?
张广铭: 根据量子力学,微观粒子大体分成两类,玻色子和费米子.玻色子系统有一个非常本质的性质就是玻色-爱因斯坦凝聚,无相互作用玻色系统会发生玻色-爱因斯坦凝聚.实际上,对于有相互作用的玻色子系统也会有凝聚现象发生,本质上与玻色-爱因斯坦凝聚相同,这个现象叫超流.超流的主要特征体现在量子流体粘滞系数消失.
再来说超导.超导是针对费米子系统的,费米子系统不会有玻色-爱因斯坦凝聚,但是当电子形成Cooper对后会形成凝聚,所以Cooper 对的凝聚就是超导.通常,超流是指不带电的粒子体系,其中的玻色子都是不带电的粒子,所以它不会有电阻消失的现象,但是它有粘滞系数消失的现象.因此,超导与超流并没有本质上的区别.
王青: 超导和超流只是一个带荷一个不带荷,把荷去掉从流动的角度都是一样的.
张广铭: 完全一样.微观粒子一旦变成满足玻色统计后,它就一定会有量子凝聚现象的发生,所以它的内在机制应该是一致的,当然我们这里讲的超导是所谓的常规超导体.因为1987年发现的高温超导体,2008年发现的铁基超导体,其中的超导微观机理目前还不确定.
王青: 在超导和超流的物理描述里,哪些是用经典理论就可以描写的?哪些是一定要用量子理论才能描写的?
张广铭: 超导和超流一样,它们都是一个对称性破缺的相变,没有经典对应.它们破缺的对称性叫做规范对称性,与粒子数守恒相联系.从正常态到超导或超流态,规范对称性破缺,我们通常用一个复变函数来描述相变,对应玻色系统的波函数或费米系统中Cooper对的波函数.复变函数作为一个序参量来描述的相变,虽然序参量的振幅可以用朗道-京兹堡自由能描述,但是当讨论序参量的相位动力学的时候,相关的物理性质就必须用量子理论,无法用经典理论.因为我们在量子力学里量子凝聚相是有相位相干性的.从量子力学的观点看相位和粒子数是一对共轭量,它们之间满足不确定关系,它们在通常的经典理论中是对易的,相位和粒子数算符在量子力学中是不对易的.
王青: 这个不对易性有什么可观察的效果吗?
张广铭: 在超导、超流体系可以观测到很多与相位相关的物理效应.比如,两块超导体中间用绝缘薄层隔开,由于两个超导体序参量的相位不同,有相位差,在没有外加电压下就会在两超导体之间产生电流,称为Josephson效应.为什么在超导中相位是一个确定值?是因为超导中粒子数是不守恒的,所以粒子数的不确定性是无穷大,相位就是一个确定值,这就是不确定关系的体现.
5 中国学者与本年度诺贝尔物理学奖
王青: 请介绍一下国内与本次诺奖工作的相关研究工作、研究组和研究人员.
张广铭: 刚才我们提到了量子霍尔效应在没有外加磁场可以实现整数量子霍尔效应.1988年Haldane提出了一个理论模型说这在理论上可以实现,但是毕竟是个理论模型,在什么材料中可以发现这个效应,还是未知的.中国科学院物理所方忠、戴希与斯坦福大学张首晟合作提出,在拓扑绝缘体材料中引入磁性杂质,可以实现不加外磁场,就能产生整数量子霍尔效应.后来,清华大学的薛其坤老师组,受到理论的启发做了相应的实验.但是,在做材料的过程中发现了一系列的困难,经过他们自己长期艰苦的探索最后找到了合适的材料体系,最后实验发现的材料并不是最初理论计算给出的,要比那个复杂.最后,在2012年做出了量子反常霍尔效应,这个工作在诺贝尔奖材料中被引用来说明1988年Haldane理论工作的正确性,表明这个实验结果确实受到了国际上的承认.
王青: 在凝聚态物质的拓扑性质方面,除了本次获奖的3位物理学家外,能否点评一下如果以后再在这个方向授奖,可能有哪些物理学家的工作会列候选?
张广铭: 我觉得有关拓扑物态的研究,最近几年得到了很大的发展,今后会有持续的发展.像拓扑绝缘体、Dirac半金属、外尔半金属和量子拓扑序都是凝聚态物理学研究的重要课题,这方面的理论和实验进展非常大.像张首晟、文小刚、薛其坤他们的工作都是世界级的研究成果.特别需要指出的是,文小刚老师获得2017年度的美国物理学会Buckley物理奖,这个奖在国际上是非常大的奖项.颁发给他的原因是他在量子拓扑序方面的杰出贡献.文小刚老师的工作还有很多,像我们刚才讲到的对量子拓扑态边缘激发的工作,实际上是文小刚老师早期做出的重要工作之一.以往获得Buckley奖的物理学家,都有很大可能得诺贝尔物理学奖的.(张首晟前几年也曾因拓扑绝缘体的工作获得Buckley奖).薛其坤老师的工作也是非常重要的,除了量子反常霍尔效应以外,薛老师用分子束外延技术研究高温超导体方面的工作,最近几年在国际上影响更大.我想,他们的实验工作今后在国际上得大奖的机会还是非常大的.特别是,薛老师的工作是研究界面超导,界面还是一个二维体系.
王青: 刚才你说的薛老师高温超导、量子反常霍尔效应,前段时髦的外尔半金属他们是一个层次的吗?
张广铭: 这个很难评定,因为有些工作需要时间,需要看后面的发展和影响.对未来的影响有多大,这是评判科研工作的一个重要的标准,而不是在当下去评判它.
6 本年度诺奖内容与大学物理教学
王青: 请你点评一下,你觉得哪些内容适于在大学物理层次进行讲解?特别是对那些非物理专业的学生.
张广铭: 我想,大学物理在教电磁学的时候都会讲霍尔效应,它是经典的霍尔效应,在那里应该加入量子霍尔效应的内容.就像我刚才给出的量子霍尔效应图像,我们可以通过比较图像化的方式来给同学们解释.量子霍尔效应实际上是可以在电磁学里面做介绍的,这个介绍可以针对物理系的学生在普通物理课程中介绍,或者针对非物理系的学生在大学物理课程里面讲,我觉得是可以的,并且是重要的.
另外,拓扑的概念也可以进入课堂.一个纯数学的概念引入到物理学,在20世纪末到今天,对整个物理学产生了重大的影响.在这之前,大家都觉得拓扑这种纯数学的概念不可能跟物理有什么关系,就像当初量子力学建立的时候把线性代数、矩阵、群等概念引入到物理学来,最后对量子论的建立和发展起了很大作用.所以拓扑概念进入物理学是非常重要的,非常深刻的.当前物理学前沿的一些研究,凝聚态或者场论、粒子物理也好,有关拓扑方面的内容都是非常多的,也是非常重要的方面,所以这个是可以讲的.如果讲授固体物理的话,当中应该介绍一下拓扑绝缘体.因为在固体的能带论当中,我们只对固体材料分成金属、半导体、绝缘体,拓扑是对绝缘体的进一步划分,分成能带绝缘体与拓扑绝缘体,这就表明人们对自然界的认识有了进一步的提高.我想这两方面的内容,都是可以进入到大学本科的教学当中去的.据我所知,加州大学伯克利分校的教授讲固体物理的时候已经把这些东西融入到他们的教学当中去了,所以我觉得国内也应该跟上时代的发展.
王青: 从你的角度对本次诺奖工作能得到些什么启示?
张广铭: 数学跟物理的联系始终是很密切的,经典力学中的牛顿第二定律: 力=质量*加速度,力是一个物理量,加速度是位移的二阶导数,牛顿的贡献就是把物理与数学联系起来了.位移的二阶导数与力是成正比的,它的比例系数就是惯性质量,有人说这是牛顿最大的贡献.爱因斯坦建立的爱因斯坦场方程,一边是引力,一边是空间的曲率,他是把物理的引力与几何空间的曲率联系起来了,这是爱因斯坦最大的贡献,所以数学跟物理是紧密联系的.
王青: 所以你这拓扑里面一边是拓扑,另一边是什么?
张广铭: 量子霍尔电导.在二维空间霍尔电导就对应着拓扑学当中的拓扑不变量——陈数.我想数学还是非常重要的.据我了解,这3位获奖科学家数学都很好,他们都是从英国移民到美国的.我个人也在英国工作过,英国的基础教育与大学教育非常重视数学,他们出了很多以数学擅长的理论物理学大家.所以我觉得最大的一个启示,不能忽视数学在建立物理学新理论中所起的重要作用.
王青: 拓扑这个事情非常重要,是不是应该把拓扑及相关的内容列为物理系学生的教学必修课里?
张广铭: 应该的.因为物理学很多的研究方向都会用到微分几何的一些概念,在拓扑物态的研究中微分几何是离不开的,现在物理系的本科生教学中是没有这方面的课程的,也是欠缺的地方.
王青: 今天的采访收获很大,谢谢张教授的讲解。
■
PROFESSOR GUANGMING ZHANG’S VIEW ON THE 2016 NOBEL PRIZE IN PHYSICS
Zhang Guangming
(Department of Physics, Tsinghua University, Beijing 100084)
张广铭. 解析2016年诺贝尔物理学奖[J]. 物理与工程,2016,26(6):3-10.
张广铭,1963年10月生于北京,1991年获上海交通大学凝聚态物理学博士学位,曾先后在国际理论物理中心(意大利)和伦敦帝国理工学院任研究助理.1997年底回国,任清华大学高等研究中心研究员,2004年至今, 任清华大学物理系教授,现任清华大学低维量子物理国家重点实验室副主任.张广铭教授长期从事凝聚态理论研究,在发展关联电子体系中近藤(Kondo)共振现象的理论和建立低维拓扑量子物态的理论体系等方面做出过系统性和原创性的研究成果.1999年获求是基金“杰出青年学者”奖,2001年获“国家杰出青年基金”,2006年被教育部聘为“长江学者特聘教授”,2011年获中国物理学会“叶企孙物理奖”.
采访日期: 2016-11-15
