一维六方准晶中界面裂纹与位错的交互作用*

肖万伸，欧阳成，张春雨

(湖南大学 机械与运载工程学院，湖南 长沙 410082)

一维六方准晶中界面裂纹与位错的交互作用*

肖万伸*，欧阳成，张春雨

(湖南大学 机械与运载工程学院，湖南 长沙 410082)

应用复变函数的方法，研究了一维六方准晶双材料中单个圆弧形夹杂界面裂纹与基体中螺型位错之间的交互作用问题，求得了该问题的封闭形式解.当界面裂纹消失时，所得的退化结果与已有文献一致.导出了位错在圆外无限大区域中的任意位置时，界面裂纹尖端应力强度因子的表达式.数值结果表明，随着位错距离界面裂纹的位置越来越远，裂纹尖端应力强度因子的值越来越小；随着界面裂纹开口角度的增大，裂纹尖端应力强度因子的值先增大后减小.

准晶；界面裂纹；螺型位错；应力强度因子；复变函数方法

1984年，Shechtman等人发现准晶.一直以来，准晶以其独特的物理力学性能和未来良好的应用前景，使其无论是在理论研究还是在实验观察方面，都吸引着广大研究者的关注[1-5].然而，准晶复合材料中的缺陷问题，如位错、裂纹、夹杂等会极大地影响到材料的力学性能.

近些年来，越来越多的科研人员开始研究准晶中的缺陷问题.Fan等[6]应用复变函数的方法研究了一维六方准晶中运动的Griffith裂纹问题；Wang等[7]研究了十次准晶中半无限裂纹与刃型位错的干涉效应问题，并求得了裂纹尖端的应力强度因子和应变能释放率的表达式；Hu等[8]研究了一维六方准晶中螺型位错与圆形夹杂的弹性干涉问题，并揭示了位错力与相位子场弹性常数和声子场-相位子场耦合弹性常数之间的变化规律.这些研究大多是针对单一缺陷问题或者单一准晶材料中的缺陷问题，对于准晶复合材料中缺陷之间的干涉效应问题，报道的比较少.

本文研究了一维六方准晶双材料中单个圆弧形界面裂纹与基体中螺型位错之间的交互作用问题.运用复变函数的解析延拓技术与奇性主部分析方法，获得了该问题的封闭形式解.在得到界面裂纹尖端应力强度因子的表达式后，讨论了裂纹尖端应力强度因子分别与裂纹开口角度、位错相对位置的变化规律.

1 问题的描述与求解

在一维六方准晶中，当缺陷(位错、裂纹)的几何特征沿准周期方向(z轴)无变化时，其弹性问题可分解为2个相互独立的问题[9].第一个问题是经典弹性问题，已被充分研究过.因此我们仅讨论第二个反平面声子场-相位子场耦合问题，于是有：

(1)

Hzx=2R3εzx+K2ωzx,Hzy=2R3εzy+K2ωzy.

(2)

(3)

(4)

(5)

在一维六方准晶中，反平面声子场-相位子场的耦合问题可以化成2个调和方程的求解[9]，即

(6)

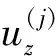
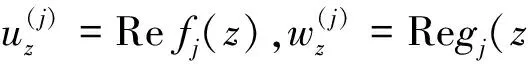
(7)

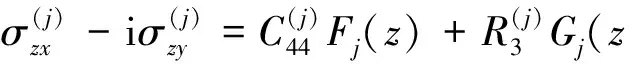
(8)

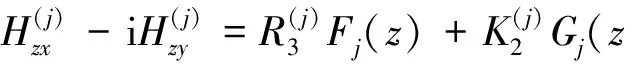
(9)

图1 圆弧形界面裂纹与螺型位错交互作用模型

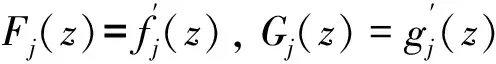
(10)

(11)

式中：D0‖, D0⊥为复常数;F10(z),G10(z)和F20(z), G20(z)在各自区域内全纯.

把式(8)(9)用极坐标的形式表示，有

(12)

(13)

在2种介质的交界面L′段上，由于圆弧形裂纹存在，所以没有面力作用，即

(14)

由式(12)(13)(14)，同时考虑式(7)可得:

(15)

(16)

根据推广的Schwarz延拓原理，并考虑到式(15)(16)可得:

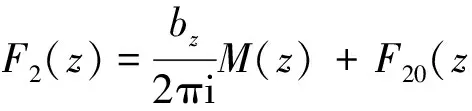
(17)

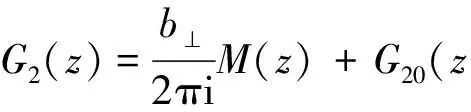
(18)

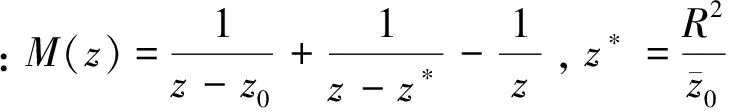
同理可得:

(19)

(20)

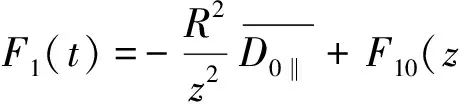
(21)

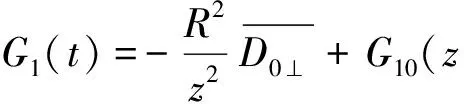
(22)

对于整个圆周交界面来说，圆内区域S+和圆外无限大区域S-两侧的应力相等，即

t∈L+L′.

(23)

t∈L+L′.

(24)

根据推广的Liouville定理，同时考虑到式(17)(18)(21)(22)，那么在全平面上有

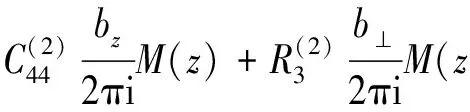
(25)

(26)

在2种介质的交界面L2段上，满足位移连续性条件，则

(27)

式(27)两边分别对α微分后，可得

(28)

即

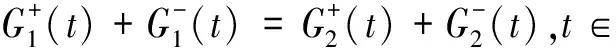
(29)

综合考虑式(25)(26)(29)，可以得到

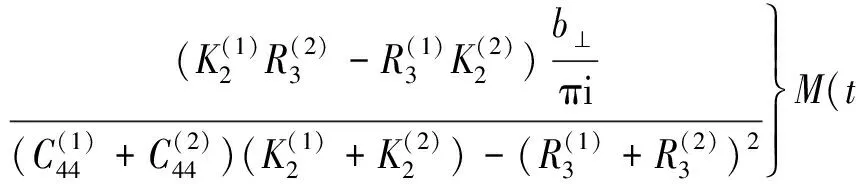
(30)

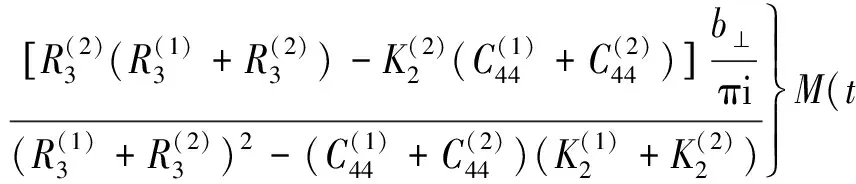
(31)

则圆内区域S+和圆外无限大区域S-的声子场和相位子场复势函数的封闭形式解答为

(32)

(33)

(34)

(35)

当α=0时，即界面裂纹消失时，得到的一维六方准晶双材料中螺型位错与界面无裂纹的圆形夹杂的干涉解答与已有文献一致[8].

2 裂纹尖端的应力强度因子

(36)

(37)

(38)

将式(32)(33)分别代入式(37)(38)，可得

(39)

(40)

3 数值分析与讨论

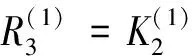
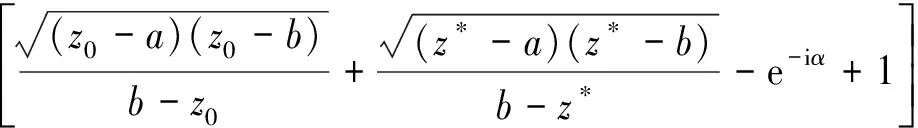
(41)

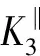
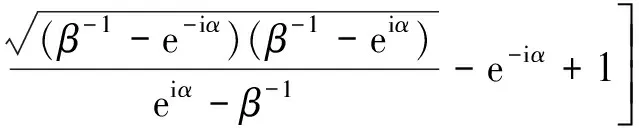
图2给出了当α取不同值时，无量纲应力强度因子K3随位错相对位置β变化的数值曲线图.从图2中可以得出，随着β逐渐增大，即位错逐渐远离界面裂纹的时候，应力强度因子K3逐渐减小.这是因为当α不变时，随着β的增大，位错离裂纹尖端就越远，那么它对裂纹尖端的影响自然就越小，所以应力强度因子就跟着逐渐减小.

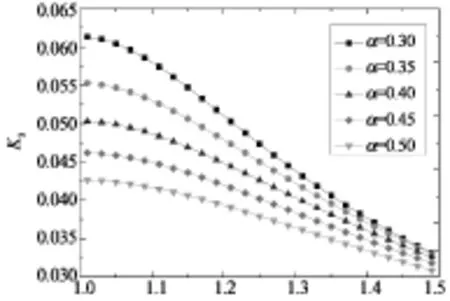
图3给出了当β取不同值时，无量纲应力强度因子K3随裂纹开口角度α变化的数据曲线图.从图3中可以得出，随着α逐渐增大，应力强度因子K3先在一定范围内急剧增大并且达到最大值，然后再逐渐减小；并且随着β逐渐减小，应力强度因子达到的最大值更大.这是因为裂纹越长(α越大)则K3越大；位错距离裂纹尖端越近(β越小)，K3也越大.但从图1可见，α越大则x轴上的位错距裂纹尖端越远(β越大)，因此存在一组(α,β)值使裂尖应力强度因子达到最大值.

β

α

4 结 论

本文研究了一维六方准晶双材料中单个圆弧形夹杂界面裂纹与基体中螺型位错之间的交互作用问题.运用复变函数的解析延拓技术与奇性主部分析方法，获得了该问题的封闭形式解.当界面裂纹消失时，所得的退化结果与已有文献一致.

在得到界面裂纹尖端应力强度因子的表达式后，讨论了圆形晶体夹杂与准晶基体的单个圆弧形界面裂纹的应力强度因子分别与裂纹开口角度、位错相对位置的变化规律.随着位错距离界面裂纹的位置越来越远，裂纹尖端应力强度因子的值越来越小；随着界面裂纹开口角度的增大，裂纹尖端应力强度因子的值先增大后减小，即存在一个特定的裂纹开口角度，使得应力强度因子的值达到最大值.

[1] LI X F, DUAN X Y, FAN T Y,etal. Elastic field for a straight dislocation in a decagonal quasicrystal [J]. Journal of Physics Condensed Matter, 1999, 11(3): 703-711.

[2] LI X F, FAN T Y. A straight dislocation in one-dimensional hexagonal quasicrystals [J]. Physica Status Solidi (B), 1999, 212(1): 19-26.

[3] RONCHETTI M. Quasicrystals—an introduction overview [M]. Philos Mag, 1987, 56: 237-249．

[4] WANG Ren-hui, YANG Wen-ge, HU Cheng-zheng,etal. Point and space groups and elastic behaviours of one-dimensional quasicrystals [J]. Journal of Physics Condensed Matter, 1997, 9(11): 2411-2422．

[5] LIU Guan-ting, GUO Rui-ping, FAN Tian-you. Plane elasticity and dislocation of one dimensional hexagonal quasicrystal with point group 6 [J]. Journal of Beijing Institute of Technology, 2005, 14(1): 87-91.

[6] FAN Tian-you. The mathematical theory of elasticity of quasicrystals and applications [M]. Beijing: Beijing Institute of Technology Press, 1999.

[7] WANG X, ZHONG Z. Interaction between a semi-infinite crack and a straight dislocation in a decagonal quasicrystal [J]. International Journal of Engineering Science, 2004, 42: 521-538.

[8] HU Ya-qun, XIA Ping, WEI Ke-xiang. The interaction between a dislocation and circular inhomogeneity in 1D hexagonal quasicrystals [J]. Applied Mechanics and Materials, 2010, 34: 429-434.

[9] 皮建东, 刘官厅, 郭怀民. 一维六方准晶中圆弧裂纹及抛物线裂纹的反平面剪切问题[J]. 内蒙古师范大学学报：自然科学汉文版，2008，37(4)：435-440.

PI Jian-dong，LIU Guan-ting，GUO Huai-min．The anti-plane problems with an arc or parabolic crack in one-dimensional hexagonal quasicrystals [J]．Journal of Inner Mongolia Normal University：Natural Science Edition, 2008, 37(4)：435-440.(In Chinese)

[10]殷景霞，方棋洪. 复合材料中的夹杂内位错和圆弧界面裂纹的弹性干涉效应 [J]. 湖南理工学院学报:自然科学版, 2003, 16(4): 37-40.

YIN Jing-xia, FANG Qi-hong. Interaction between a screw dislocation in the circular inclusion and interfacial cracks in composite materials[J]. Journal of Hunan Institute of Science and Technology: Natural Sciences, 2003, 16(4): 37-40.(In Chinese)

Interaction between Circular Interfacial Crack and Screw Dislocation in 1D Hexagonal Quasicrystals

XIAO Wan-shen†, OUYANG Cheng, ZHANG Chun-yu

(College of Mechanical and Vehicle Engineering, Hunan Univ, Changsha, Hunan 410082,China)

The interaction effects between a single circular interfacial crack and screw dislocation located inside the matrix were investigated for 1D hexagonal quasicrystal. Through applying the complex potential method, the closed form solutions of this problem were obtained. The degradation results are consistent with the conclusions in previous literature. The stress intensity factor at the crack tip was also derived. The results show that the stress intensity factor decreases with the increase of the distance between the dislocation and interfacial crack. With the increase of the opening angle of the circular interfacial crack, the stress intensity factor increases firstly and then decreases.

quasicrystals; interfacial cracks; screw dislocations; stress intensity factor; complex variable method

1674-2974(2016)12-0071-05

2016-04-21 基金项目：国家自然科学基金资助项目(11572118, 51175164), National Natural Science Foundation of China(11572118, 51175164) 作者简介：肖万伸(1959-)，男，湖南道县人，湖南大学教授，博士 †通讯联系人，E-mail: xwshndc@163.com

O346.1

A