多复变量Hilbert空间上的复合算子族的拓扑结构

仝策中，于 洋，张 建

（1.河北工业大学 理学院，天津 300401；2.河北工业大学 计算机科学与软件学院，天津 300401）

多复变量Hilbert空间上的复合算子族的拓扑结构

仝策中1，于 洋2，张 建1

（1.河北工业大学 理学院，天津 300401；2.河北工业大学 计算机科学与软件学院，天津 300401）

将在算子范数拓扑的意义下，研究多复变量函数的Hilbert空间之间的有界加权复合算子族的拓扑连通性．利用类似的方法还将研究在 Hilbert-Schm idt范数拓扑下的连通性．这些讨论与结论适用于多种多复变量函数空间，比如Hardy空间，Bergman空间Dirichlet空间之间的加权复合算子族的拓扑结构的研究．

多复变量；Hilbert空间；加权复合算子；道路连通；算子范数；Hilbert-Schm idt范数

1 基本概念和符号

复合算子理论的研究应该追溯到20世纪60年代中期Nordgren的工作[1]．自1987年，以Shapiro在Annals Math.上发表的文献[4]为代表，复合算子的研究得到了快速和巨大的发展．感兴趣的读者可以参考专著[2-3，5]，这些论著都较系统地介绍了复合算子理论．复合算子理论在近些年主要在多复变量函数空间的基础上讨论问题，而且一个新兴的问题是将复合算子的全体赋以算子范数拓扑（或Hilbert-Schm idt范数拓扑），讨论这个拓扑空间的连通性．对复合算子的拓扑结构和缠绕性质感兴趣的读者可以参考近些年的文献[6-12]．2015年[13]，T.Hosokawa，K.Izuchi和S.Ohno研究了单位圆盘上的Hilbert函数空间上的加权复合算子的拓扑结构，由于多复变量的函数与单复变量的函数本质上存在很多不同，基于这个动机，本文研究了高位超球上的Hilbert函数空间上的加权复合算子的拓扑结构．

设N维复欧式空间CN中的单位超球为

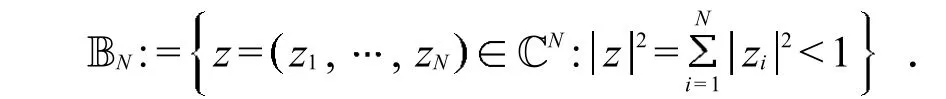
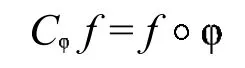
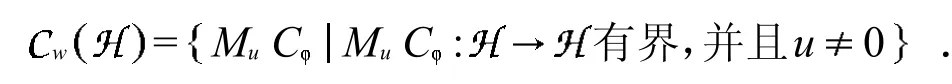
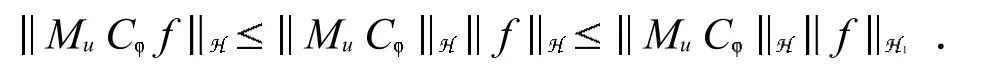
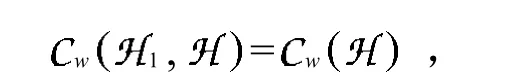
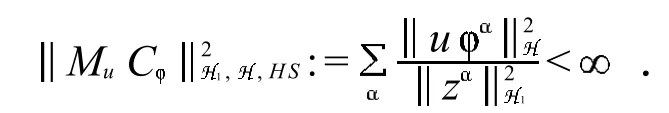
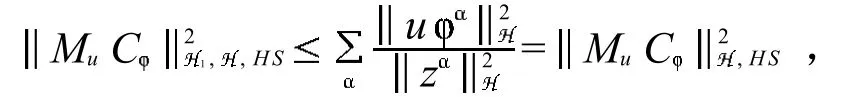
2 拓扑空间

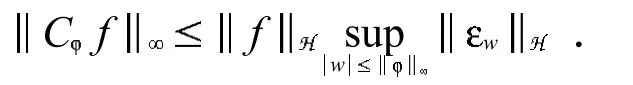
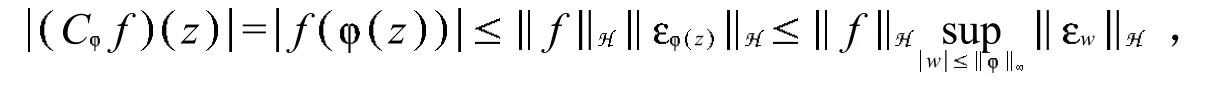
证毕．

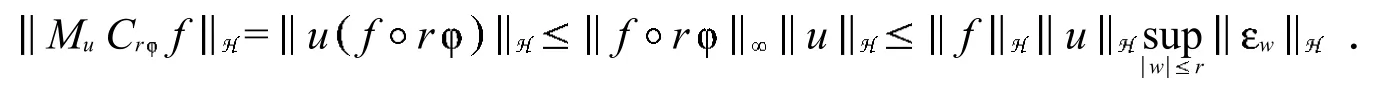
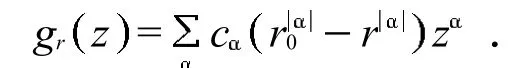
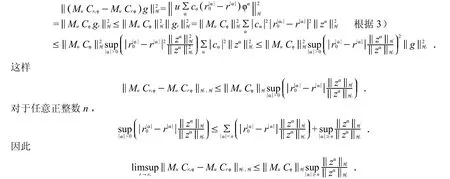
根据假设，当r r0时，在中有．这意味着在中是一个道路连通子集．

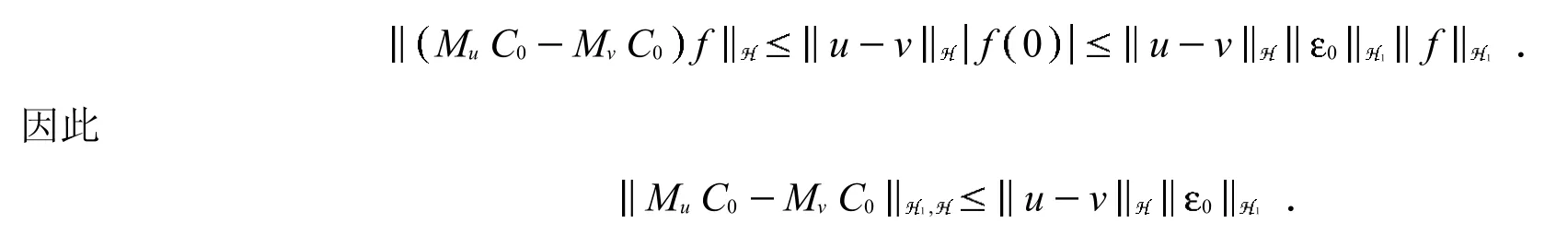
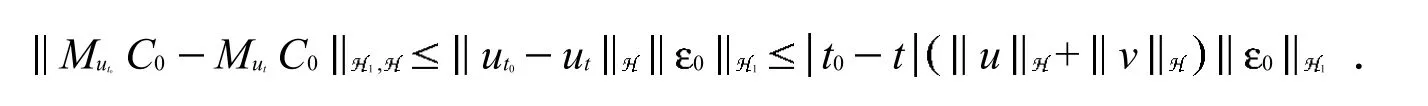
要说明MuC是紧算子，这里利用文献 [2]中的Proposition 3.11的结论来证明．如果 fn是中的有界函数列，即存在K＜0，使得对于任意n， fn＜K．根据条件1），可以设fn在BN上内闭一致收敛于某个．根据条件 ＜1，有fnf 在H中．再由条件2），，且有

3 拓扑空间的道路连通性

证明 可以通过下面的计算直接得到证明：

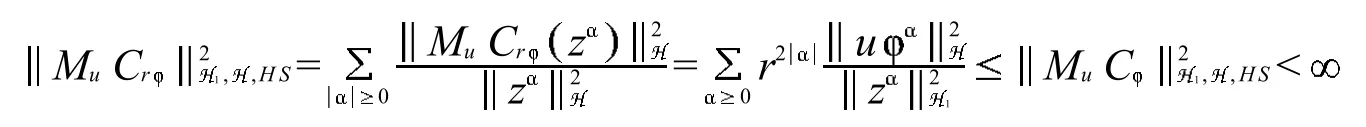
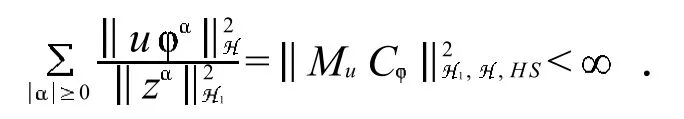
任取δ＞0，则根据方程 (2)，可以取充分大的自然数N使得

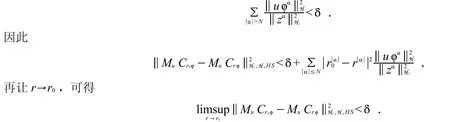
由此得到，当r r0时，．因此MuC 与MuC0在的同一道路连通分支中．

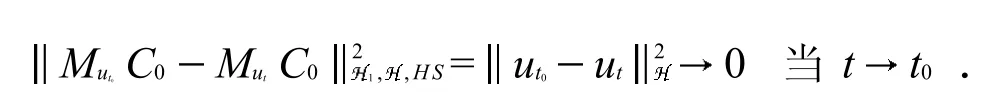
因此MuC0和MvC0在中的同一道路连通分支中．所以任意的和MvC都是处于中的同一道路连通分支中．

4 理论应用

用d v表示BN上的标准化的Lebesgue体测度，即有．单位球面SN的标准化Lebesgue面测度记为，即有．这两个标准化常数分别是BN的实际体积和SN实际面积．本节用符号表示经典BN上的Hardy-Hilbert空间，即由所有满足下面条件的BN上的全纯函数构成的函数空间

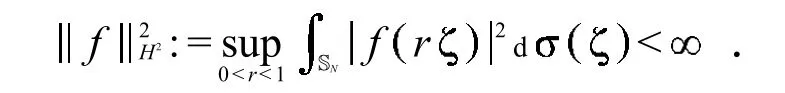
容易验证空间H2满足条件1）～4），并且

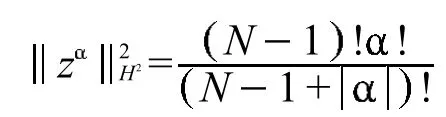
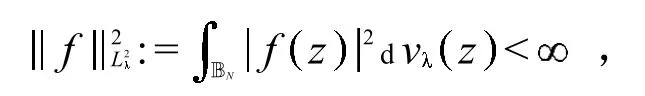
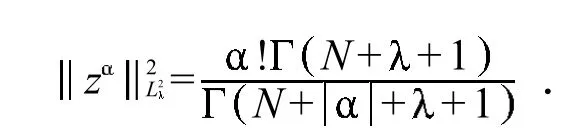
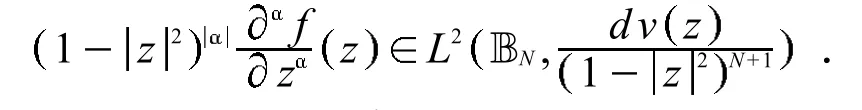
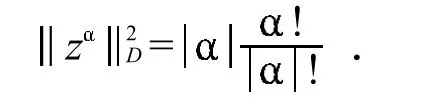
上述多复变量函数空间的基本概念和结论均可在文献 [5]找到详细论述．

经过计算

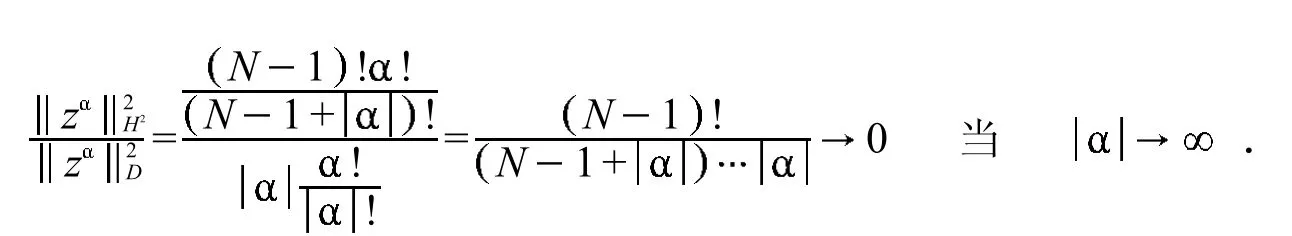
由Stirling公式，

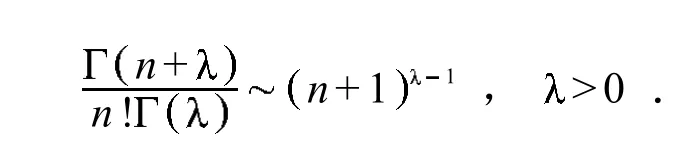
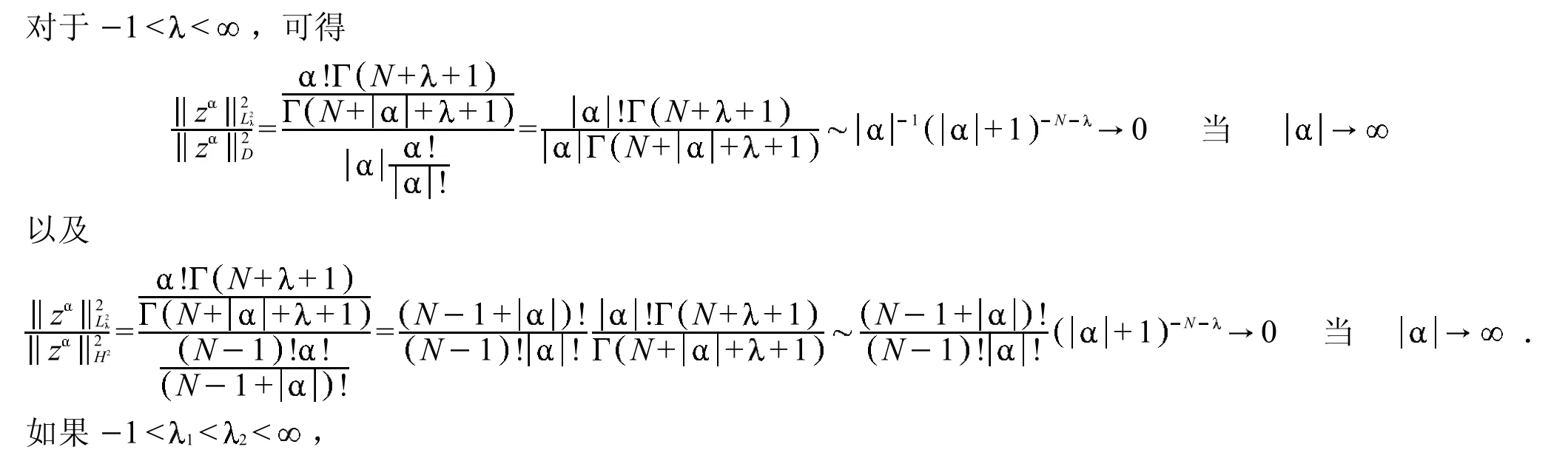
再由定理1和定理2，可得下面2个直接推论．

[1]Nordgren EA．Composition operators[J]．Canadian JournalofMathematics，1968，20：442-449．

[2]Cowen CC，MacCluer BD．Composition Operatorson Spacesof Analytic Functions[M]．Boca Raton：CRC Press，1995．

[3]Shapiro JH．Composition Operatorsand Classical Function Theory[M]．New York：Springer Verlag，1993．

[4]Shapiro JH．Theessentialnorm of a composition operator[J]．AnnalsMath，1987，125（2）：375-404．

[5]Zhu K H．Spacesof Holomorphic Functions in the UnitBall[M]．Grad Texts in Math，Springer，2005．

[6]Tong C，Zhou Z．The compactnessof the sum ofweighted composition operatorson theballalgebra[J]．Journalof Inequalitiesand Applications，2011，Article Number45，DOI：10.1186/1029-242X-2011-45：1-10．

[7]仝策中，周泽华．单位圆盘代数上的加权复合算子的有限和 [J]．数学物理学报，2012，32A（6）：1102-1109．

[8]Tong C．Comopactdifferencesofweighted composition operatorson H BN[J]．Journalof ComputationalAnalysisand Applications，2012，14 （1）：32-41．

[9]Tong C，Zhou Z．Intertw ining relations forvolterraoperatorson thebergman space[J]．Illinois1JournalofMathematics，2013，57（1）：195-211．

[10]Tong C，Zhou Z．Compact intertwining relations for composition operators between theweighted bergman spaces and theweighted bloch spaces [J]．Journalof Korean MathematicalSociety，2014，51（1）：125-135．

[11]Yuan C，Tong C．Distance from bloch-type functions to theanalytic space F p,q,s [J]．Abstractand Applied Analysis，2014，ArticleNumber 610237，DOI：10.1155/2014/610237：1-10．

[12]Tong C，Yuan C．An integraloperatorpreserving s-Carlesonmeasureon theunitball[J]．AnnalesAcadem iaeScientiarum FennicaeMathematica，2015，40：361-373．

[13]Hosokawa T，Izuch K，Ohno S．Weighted composition operators between Hilbert spaces of analytic functions in the operator norm and Hilbert-Schmidtnorm topologies[J]．JournalofMathematicalAnalysisand Applications，2015，421：1546-1558．

[责任编辑 杨 屹]

Topologicalstructure of composition operatorson Hilbertspaces in severalcomplex variables

TONGCeZhong1，YU Yang2，ZHANG Jian1

(Schoolof Science,HebeiUniversity of Technology,Tianjin 300401,China;2.Schoolof Computer Scienceand Engineering,Hebei University of Technology,Tianjin 300401,China)

The topological connectednessofweighted composition operatorsbetween the Hilbertspaces in several complex variablesare studied.These resultsare applied to characterize the topologicalstructure ofweighed composition operatorsacting between Hardy spaces,Bergman spacesand Dirichletspacesofseveralcomplex variablesholomorphic functions,which generalizes the resultsof T.Hosokawa,K.Izuchiand S.Ohno.

severalcomplex variables;Hilbertspaces;weighted composition operators;connectedness;operatornorm; Hilbert-Schmidtnorm

O174.56

A

1007-2373(2016)01-0051-06

10.14081/j.cnki.hgdxb.2016.01.010

2015-01-08

国家自然科学基金（11301132，11171087）；河北省自然科学基金（A2013202265）

仝策中（1984-），男（汉族），讲师，博士．

张建（1982-），男（汉族），实验师．