自我解释和样例呈现类型对小学生数学学习的影响*

任金杰，李绍蕾

(通化师范学院教育科学学院，吉林通化134002)

自我解释和样例呈现类型对小学生数学学习的影响*

任金杰，李绍蕾

(通化师范学院教育科学学院，吉林通化134002)

本研究选取了小学五年级88名学生为被试，采用2×2区组实验设计，以小数的四则运算为学习材料，探究自我解释和样例呈现类型对学习状况不同的小学生数学学习的影响.结果表明:(1)自我解释在绩优组学生的概念掌握上有明显的主效应;(2)样例呈现类型在绩困组和绩优组均无主效应;(3)在绩优组远迁移问题的解决上，自我解释和样例呈现类型存在明显的交互作用，即有自我解释的情况下，基于过程呈现的效果要明显好于基于结果呈现，而在无自我解释的情况下，基于结果呈现的效果要明显好于基于过程呈现.

自我解释;样例呈现类型;数学学习

1 引言

样例学习是教育心理的重要研究领域，早期的样例学习研究都假定:样例加工方式不存在个体差异，不重视学习者在学习样例时候可能使用有效的学习策略.1989年，Chi及其同事提出自我解释效应［1］，从而引发了人们对样例学习中个体差异的关注，大量学者投身到自我解释的研究.

1.1 自我解释及其研究发展

在教学情景中，自我解释(self－explaining)被定义为任何学习者向其自身作出解释，以此力图理解新信息的活动.［2］Chi及其同事的实验发现，在样例学习中的自我解释与测验成绩呈显著正相关，并将这种现象称为自我解释效应［3］.Chi认为自我解释是一种具有建构性的推理活动，具有连续性、片段性的特点，自我解释的重点在于理解学习材料和搞清学习材料的意思，它有较多的思考和精加工活动，它不仅有助于改善不完整的文本，还有助于修补心理模型，因此自我解释能提高学习效果.

经过二十几年的发展，自我解释研究的重点由验证自我解释效应，探究自我解释效应的认知机制及自我解释的特点，逐步转向自我解释的应用研究，并取得了可喜的成果.如:Conati和VanLehn(1999)比较了使用自我解释辅导系统组和对照组的被试成绩，两组之间没有统计上的差异.Crippen等在基于网络的样例学习研究中发现，采用样例和自我解释干预有助于提高学生成绩.我国学者柏宏权通过实验也证实，在网络学习环境中使用自我解释支持工具有助于学生知识的的建构和知识的整合.［4］Rittle －Johnson(2006)结果发现自我解释有助于学生学习正确的方法，能促进学习迁移，不能有效地促进概念的掌握，自我解释与有效的认知过程紧密相联.［5］Rittle－Johnson的研究与Klahr等人的研究结论一致，但与Chi(2000)某些观点相悖.由于自我解释本身的复杂性和研究设计的差异性，以往研究成果存在一定的分歧和矛盾，需要后续的研究进一步验证.

1.2 样例学习及样例呈现类型

样例学习(learning－by－example)是指从详细

Van(2004)在研究样例对学习迁移的影响中，提出了基于过程的样例(process－oriented worked example)和基于结果的样例(product－oriented worked example).基于过程的样例就是提供有专家在问题解决过程中运用的规则和策略知识的实例.而基于结果的样例则是提供有专家有效解决问题结果的样例.Tamara van Gog(2004)的实验研究发现，虽然基于过程的样例学习可以促进问题解决的迁移，但是这种影响仅存在于开始阶段，随着学习的深入，这些过程信息反而阻碍了问题的有效解决.［7］

1.3 问题提出

自Chi提出自我解释效应以来，自我解释研究经过十几年的发展，取得了很多成果，研究工作已由最初探讨自我解释的内涵机制，验证自我解释效应的存在，发展到关注自我解释在教学中应用和训练问题.尤其是样例呈现类型与自我解释的结合已成为学习迁移研究的新热点.国内外学者对此进行了大量的研究和探讨，并提出许多能有效促进学习迁移和问题解决的样例设计观点和模型，但是关于样例呈现类型与自我解释关系的研究还较少，且研究对象多是中学生和大学生，针对小学生的很少.所以，本研究选择用小学生作为研究对象，通过实验，探究自我解释和样例呈现类型对学习优秀和学习不良小学生的数学学习的影响.

2 方法

2.1 实验设计

本研究采用的是2×2区组实验设计，根据被试的学习状况，将被试分两个区组，即绩优组和绩困组;自变量包括自我解释、样例呈现类型，A因素为自我解释，分为有自我解释和无自我解释两个水平; B因素为样例呈现类型，分为基于结果呈现和基于过程呈现.因变量为学生学习的成绩，将其分为三个指标，概念原理的掌握、近迁移和远迁移的学习成绩.

2.2 被试

选择通钢三小五年级的学生为被试，根据上学期期末考试成绩排名，选择前27%和后27%的学生，共92人.通过前测将不符合要求的学生剔除，选择符合条件的被试88人，其中成绩优秀的44人，成绩困难的44人.

2.3 实验材料

(1)前测材料.为了保证被试均没有学习过新知识，且对小数计算的基础知识掌握情况一致.我们根据人教版小学五年级教材中的小数混合运算，设计了前测材料.前测材料分为两大部分，第一部分为填空题，即有关四则运算的概念填空题，第二部分为计算题，总共七道计算题，其中前四道是小数加减乘除题，用来检验学生对于基础知识的掌握情况;后三道为小数四则混合运算题，用于检验学生是否学习过新知识.根据测试结果剔除前四道题不正确和后三道正确的学生，即剔除基础知识掌握不好和学习过新内容的学习.

(2)干预期的学习材料.样例材料是根据小学五年级教材进行编排的，分为四种，一种是有自我解释加上有过程的样例的练习，另一种是无自我解释加上有过程的练习，第三种是有自我解释加上只有结果的样例的练习，第四种是无自我解释加上只有结果的样例练习.在试卷上呈现材料，先呈现指导语，然后是“样例一”，接下来是“练习一”“样例二”和“练习二”.

(3)后测材料.后测数学测试题分为两个部分，一部分为描述性概念原理问题，用于考察实验处理后学生对于概念原理知识的掌握情况.概念题总共三道，五个空，每个空1分，共5分.计算题总共6道，三道近迁移，三道远迁移，每题3分，总共18分.

2.4 实验程序

(1)前测分组.根据学生上学期期末学习成绩和班主任意见选取44名学习优秀的学生和44名学习困难的学生，形成两个区组，即绩困组和绩优组，之后让两个区组的被试分别接受四种条件的实验处理，即“解释+过程呈现”“解释+结果呈现”“无解释+过程呈现”和“无解释+结果呈现”.

(2)样例学习阶段.所有的被试都参与学习样例材料，不同的组使用不同的学习材料，样例学习阶段的材料均为样例和练习交互呈现，指导语为:“你好!这是一份关于小数问题的问卷.其中例1和例2已经给出答案，请参照例1和例2的步骤，做出练习1和练习2，该问卷只做研究使用，不会记录你的成绩，请认真作答，谢谢合作!”

“解释+过程”组，有详细的解题步骤，提醒学生认真学习样例解题步骤，思考解题思路，为什么这样做，并要求在练习时进行自我解释.

“解释+结果”组，仅有简单的解题步骤，提醒学生认真学习样例解题步骤，思考解题思路，为什么这样做，并要求在练习时进行自我解释.

“无解释+过程”组，有详细的解题步骤，鼓励学生根据样例题目，认真学习解题步骤，但不要求进行自我解释.

“无解释+结果”组，仅有简单的解题步骤，鼓励学生根据样例题目，认真学习解题步骤，但不要求进行自我解释.

为了保证实验条件的相同，提高实验结果的效度，每组的学习材料和练习材料都是相同的，过程组比结果组步骤更为详细，解释组在练习材料上有提示必须进行自我解释.本阶段共有四道题，一道简单的样例加上简单的练习，一道复杂的样例加上复杂的练习.每个组的实验均为25分钟，在同一间教室严格按照实验设计进行并完成.

2.5 编码与数据处理

(1)内容分析、编码.根据学生在后测卷子中的作答情况了解被试对于概念原理的掌握情况.概念原理题总共5分，每个空1分.计算题总分18分，每题3分.每题的计分规则依据解题步骤的正确性给分.

(2)数据处理.使用SPSS11.5对数据进行数据处理，采用方差分析研究自我解释、样例呈现类型对小学生数学学习的影响.

3 结果与分析

对绩优组和绩困组的学生进行数据处理，分别考察自我解释与样例呈现类型对绩优生和绩困生的概念原理的掌握、近迁移和远迁移成绩的影响.

3.1 自我解释在各因变量上的主效应

对于被试在自我解释的影响下的概念原理、近迁移、远迁移成绩进行方差分析，其结果统计(见表1和表2).

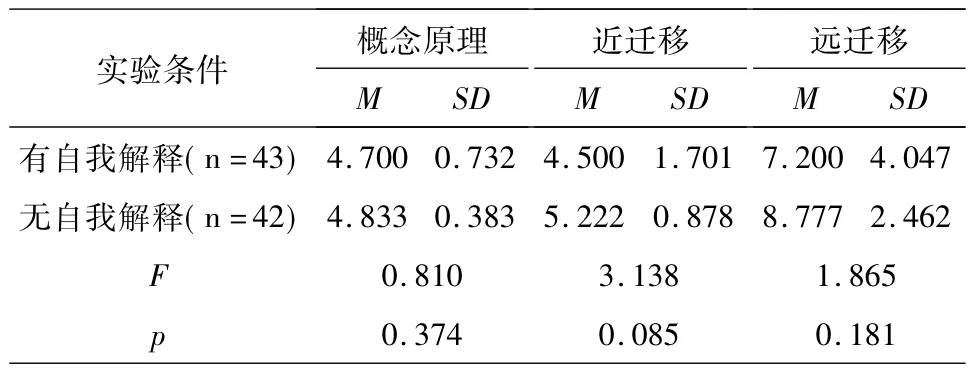
表1 自我解释在绩困组各因变量上的方差分析

通过方差分析结果可以看出，自我解释对于绩困组学生的概念原理掌握无主效应(F=0.81，p＞0.05)，即自我解释在概念原理的掌握上无显著性差异.近迁移成绩上也无主效应(F=3.138，p＞0.05)即自我解释在近迁移成绩上没有显著性的差异.在远迁移成绩上也没有主效应(F=1.865，p＞0.05).说明自我解释在远迁移成绩上也没有显著性的差异，即自我解释对远迁移成绩没有促进作用.此外，自我解释对概念原理的掌握和近迁移成绩没有明显的影响.

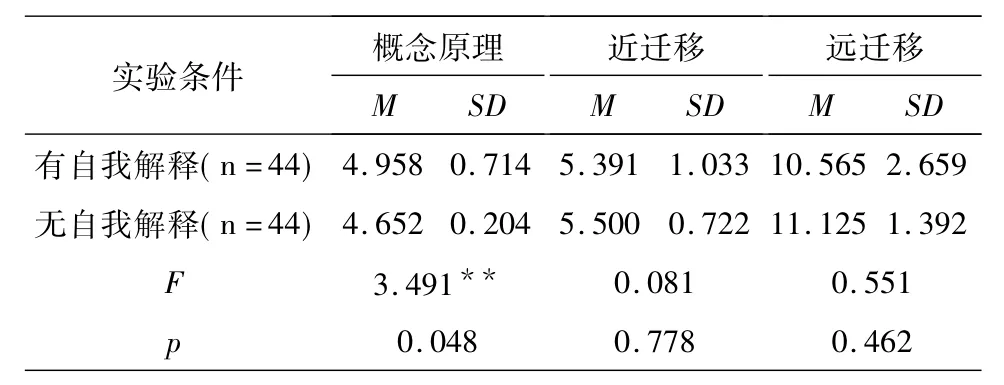
表2 自我解释在绩优组各因变量上的方差分析

在绩优组中，自我解释在概念原理的掌握上有主效应(F=3.491，p＜0.05)，即在概念原理的掌握上，解释组的成绩显著高于无解释组的成绩.在近迁移成绩上无主效应(F=0.081，p＞0.05)，即自我解释在近迁移成绩上没有显著性差异.在远迁移成绩上也没有主效应(F=0.551，p＞0.05)，即自我解释在远迁移成绩上没有显著性差异.以上结果说明:对学习优秀的学生，自我解释对概念原理的掌握有一定的促进作用，但对近迁移和远迁移成绩没有影响.

3.2 样例呈现类型在各因变量上的主效应

将被试在不同样例呈现类型下的概念原理分数、近迁移、远迁移成绩进行方差分析(见表3和表4).

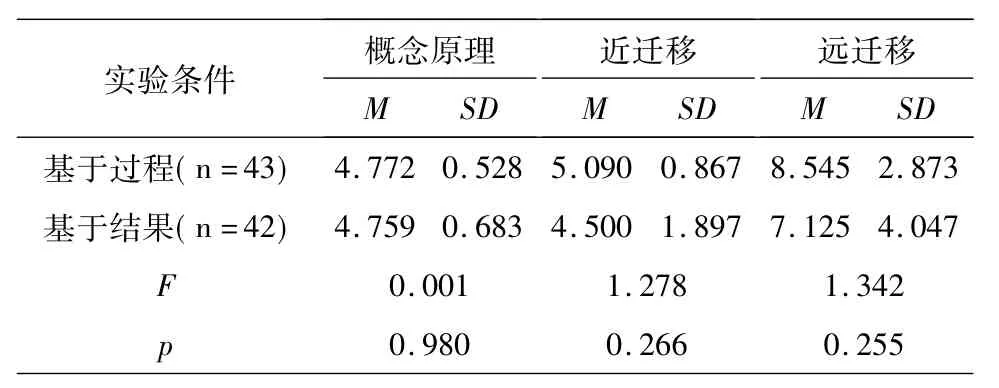
表3 样例呈现类型在绩困组各因变量上的方差分析

结果表明:无论是在绩困组中还是绩优组中，样例呈现类型在概念原理的掌握(F困=0.001，F优= 3.084)、近迁移成绩(F困=1.278，F优=0.171)和远迁移成绩(F困=1.342，F优=0.593)上都没有主效应，这说明样例呈现类型对小学生数学概念原理掌握和近远迁移问题的解决均没有明显的影响作用.

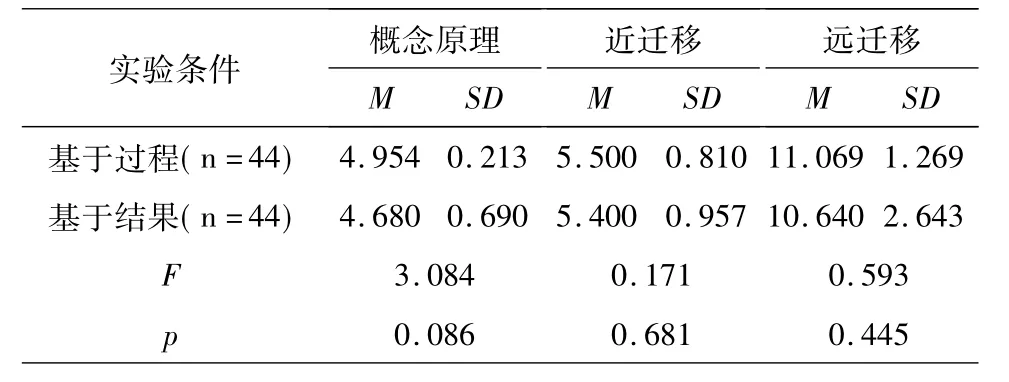
表4 样例呈现类型在绩优组各因变量上的方差分析

3.3 自我解释和样例呈现类型在各因变量上的交互作用

结合方差分析结果，进一步分析绩困组和绩优组自我解释和样例呈现类型在各因变量上是否存在交互作用(见表5和表6).

结果显示，在绩困组中，自我解释和样例呈现类型在概念原理掌握(F=1.857，p＞0.05)、近迁移成绩(F=1.859，p=＞0.05)和远迁移成绩(F= 0.057，p＞0.05)上均无明显的的交互作用，即自我解释和样例呈现类型对绩困组学生概念原理掌握和迁移问题解决的影响是相互独立的.

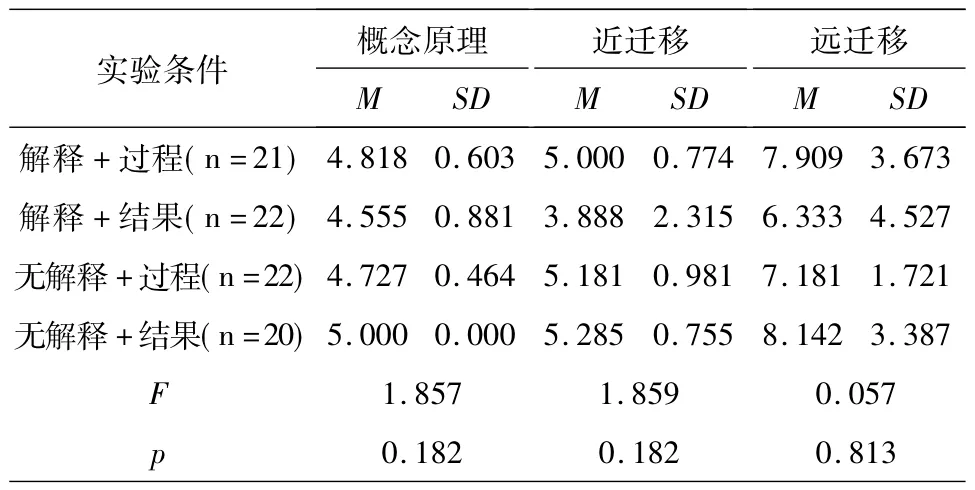
表5 自我解释和样例呈现类型对绩困组学习的交互作用分析

在绩优组中，自我解释和样例呈现类型在远迁移成绩上有显著性的交互作用(F=5.359，p＜0.05)，即自我解释对绩优组学生远迁移问题学习的影响样例呈现类型的影响.进一步简单效应分析结果显示，在学生进行自我解释的情况下，基于过程呈现的效果要明显好于基于结果呈现方式，而在学生无自我解释的情况下，基于结果呈现的效果要明显好于基于过程呈现.但在概念掌握(F=1.429，p ＞0.05)和近迁移成绩上(F=2.922，p＞0.05)无明显的交互作用，说明自我解释和样例呈现类型对绩优组学生概念掌握和近迁移问题解决的影响是相互独立的.

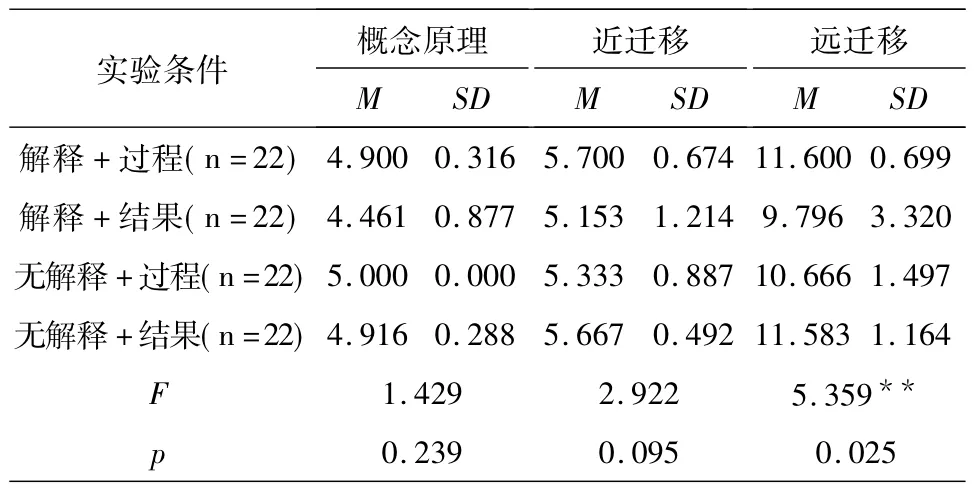
表6 自我解释和样例呈现类型对绩优组学习的交互作用分析

4 讨论

4.1 自我解释对小学生数学学习的影响

本研究发现:对于学习优秀的小学生说，在概念原理的掌握方面，存在自我解释的主效应，即进行自我解释的学生概念原理掌握成绩更好.但是对于绩困组，自我解释成为绩困组学生的负担，反而阻碍了他们对概念的记忆.这个研究与Rittle－Johnson在2006年的实验结论存在一定的差异.Rittle－Johnson认为儿童概念知识的获得是根据儿童解决问题经验的不断累加，与自我解释无关［5］.我们认为导致结果出现差异的原因是Rittle－Johnson的实验条件与教学条件之间的差异较大，而且被试也没有相关的学习材料.本研究中的实验条件和教学条件基本一致，都是在固定的教室中提供了相应的学习材料，这样可以让被试在自我解释的过程中更有效地运用相关的概念和原理.另外，本实验对于概念原理是采用书面的形式进行反馈的，很显然书面回答更能反映学生的掌握情况.

本研究的结果显示，无论是在绩困组还是绩优组中，自我解释对近迁移和远迁移的成绩均无明显的影响，该结论和Selger(2002)的研究结论相反，Selger认为自我解释能够促进更深层的思维探索［8］.导致这种差异的原因，他们选择的被试是初中生或大学生，而本研究的被试是小学生，这个年龄阶段的学生以具体形象思维为主，学生的举一反三的能力有限，单纯的自我解释并不能有效地促进学习迁移.

4.2 样例呈现类型对小学生数学学习的影响

该研究表明，无论是对于成绩优秀还是成绩不好的同学来说，样例呈现类型对小学生数学概念原理的掌握、近迁移和远迁移成绩的影响作用都不明显.这与Van在2006年的研究结论一致，即基于过程的样例学习既没有提高近迁移成绩，也没有提高远迁移成绩［9］.导致这一结果的原因可能是因为小学生的自学能力有限，学习更多地依赖教师的讲解，所以样例呈现类型并不能影响小学生的数学学习，

4.3 自我解释和样例呈现类型对小学生数学学习的影响

本研究发现，对于绩困组的同学来说，自我解释和样例呈现类型对小学生数学学习影响是独立的，这一研究结果与Rittle－Johnson的研究结论一致，即自我解释对小学生概念原理的掌握与数学问题的解决影响，不受到样例呈现类型的影响［5］.然而对于成绩优秀组的同学来说，自我解释和样例呈现类型对小学生概念原理的掌握和近迁移成绩的影响是独立的，但是自我解释和样例呈现类型在远迁移成绩上有显著性的交互作用，即在学生进行自我解释的情况下，基于过程呈现的效果要明显好于基于结果呈现方式，而在学生无自我解释的情况下，基于结果呈现的效果要明显好于基于过程呈现.这可能是因为详细的样例和积极的自我解释能更有效地促进学生的理解和问题解决，而无自我解释的情况下，详细的样例反而成为多余信息，阻碍了问题解决的迁移.

本研究结果说明自我解释和样例呈现对于绩困生没有影响，但自我解释对促进绩优生的概念原理掌握，自我解释与基于过程呈现样例的结合能促进绩优生远迁移问题的解决.因此，在小学数学学习中，教师要注意合理地应用自我解释和样例呈现.

5 结论

本研究采用2×2区组实验设计，将绩困组和绩优组中的自我解释(有自我解释，无自我解释)和样例呈现类型(基于过程，基于结果)的影响效果进行比较分析，结果如下:

(1)对于绩优组的同学来说，自我解释在概念原理的掌握上有明显主效应，即自我解释能够有效地促进学生数学概念原理的掌握.

(2)无论是绩优组还是绩困组，样例的呈现类型在各因变量上均无主效应，即样例呈现类型对概念原理的掌握和近迁移、远迁移成绩均没有明显的影响.

(3)对于绩优组的同学来说，自我解释和样例呈现类型在远迁移成绩上是存在着交互作用的.即有自我解释的情况下，基于过程呈现组的成绩要明显好于基于结果呈现组，而在无自我解释的情况下，基于结果呈现组的成绩要明显好于基于过程呈现组.在其他方面，自我解释和样例呈现类型对小学生数学学习的影响是相互独立的.

［1］邢强，莫雷.样例学习的发展及问题［J］.心理科学进展，2003(3):165－170.

［2］吴庆麟，杜伟宇.自我解释的研究［J］.心理科学，2003(11): 971－975.

［3］任金杰.样例学习方式和自我解释对大学生数学学习迁移的影响［J］.黑龙江高教研究，2009(9):188－190.

［4］柏宏权.自我解释策略在网络环境中的应用研究［J］.中国远程教育，2005(1):37－39.

［5］Bethany Rittle－Johnson Promoting Transfer Effects of Self Explanation and Direct Instruction［J］.Child Delelopment，2006(77):1－15.

［6］许永勤，朱新明.关于样例学习中样例设计的若干研究［J］.心理学动态，2000(4):18－22.

［7］赵俊峰，丁艳云.不同样例对初中生代数学习中问题解决迁移的影响［M］.河南:河南大学出版社，2009.

［8］Siegler R Microgenetic studies of self－explanation［G］//.In N Garnott＆J Parziale(Ed)，Microdevelopment:A process－oriented perspective for studying development and learning Cambridge MA:Cambridge University Press.2002:31－58.

［9］Van Merrienboer J J G，Kester L，Pass F.Teaching Complex Rather Than Simple Tasks:Balancing Intrinsic and Germane Load to Enhance Transter of learning［J］.Applied lognitive Phsychology，2006(20): 343－352.

(责任编辑:徐星华)

The Effects of Self－explaining and Worked －exam ples Presentation Form on Primary School Mathematics Learning

REN Jin－jie
(School of Education Science，Tonghua Normal University，Tonghua，Jilin 134001，China)

In this paper，88 fifth－grade students are used for subjects.At the same time，2×2×2 experiments are designed for studying the effects of self－explaining and worked－examples presentation form on primary school mathematics learning.The results showed that:firstly，self－explaining significant shows main effect on the concept acquisition of outstanding student group;secondly，worked－examples presentation form has no main effect on each dependent variable.In addition，self－explanation and workedexamples presentation form have interaction on the far transfer performance for outstanding student group.

self－explaining;worked－examples presentation form;mathematics learning

G633.6

A

1008－7974(2016)06－0108－05

10.13877/j.cnki.cn22－1284.2016.12.033解答步骤的事例中归纳出隐含的抽象知识来解决问题［6］.样例学习能有效地促进学习迁移，提高学习效率.

2016－07－21

吉林省教育厅“十二五”科学技术研究项目(吉教科合字【2013】388号);吉林省基础教育教学研究重点课题“自我解释策略在小学数学课堂教学中的应用研究”(JLSJY2012Z086)

任金杰，女，吉林通化人，副教授.