基于能量法的车辆侧翻稳定性动力学研究

黄明亮， 郑敏毅， 张邦基， 张 农， 陈盛钊

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082; 2.合肥工业大学 机械与汽车工程学院，合肥 230009)

基于能量法的车辆侧翻稳定性动力学研究

黄明亮1， 郑敏毅2， 张邦基1， 张 农2， 陈盛钊1

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082; 2.合肥工业大学 机械与汽车工程学院，合肥 230009)

利用能量方法研究车辆的侧翻性能，提出了一种新的车辆侧翻稳定性综合评价方法。建立了复杂非线性十自由度车辆动力学模型，并通过试验验证了模型的正确性。定义了车辆侧翻能量稳定指标：通过计算车辆实时能量储备与车辆侧翻的能量阈值比值得到侧翻能量储备系数，整合车速和转向输入得到车速-转向干扰系数，最终建立一个包含车速、侧倾角速度、侧倾角和轮胎转角等因素的车辆侧翻稳定性综合评价指标。最后在十自由度车辆动力学模型的基础上进行多工况仿真实验，通过与现有评价指标的对比分析，验证了该评价指标的正确性和适用性。

侧翻稳定性；动力学模型；能量阈值；能量稳定指标

车辆侧翻是一种严重的公路交通安全事故，根据美国国家公路安全交通管理局(NHTSA)近期资料[1]显示，2013年美国有将近1 000万起交通安全事故，其中2%与侧翻有关，但侧翻导致的死亡率高达33%，这使得研究车辆侧翻和提高车辆抗侧翻性能显得尤为重要。

车辆道路侧翻事故一般指动态侧翻，动态侧翻又分为绊倒型和非绊倒型[2]。绊倒型侧翻发生时，车辆不再是由车辆结构和参数决定的动力学模型，而是近似于简单的刚体运动[3]，且绊倒型侧翻往往不具有可控性。非绊倒型侧翻则由车辆自身参数、路面输入、驾驶条件和外界干扰等因素综合决定，是车辆侧翻的主要研究内容。传统的侧翻评价指标采用单纯的侧倾角度或侧向加速度[4]，该方法的实时性和精准性较差；相对于传统的侧翻评价指标而言，基于轮胎变形的估算量来判断侧翻[5]和基于侧翻时间的算法(TTR)[6]提高了侧翻评价的准确性，但这两种指标分别采用遗传算法和神经网络算法，从而导致实时性较差；目前车辆侧翻性研究多采用车辆的横向载荷转移率(LTR)[7]作为车辆侧翻评价指标，LTR及其变形能够直观地反映出车辆实时的侧倾状态，因此被业内广泛应用[8-15]。但LTR也是单纯以轮胎载荷为算子，该算法在某个车轮受到冲击或瞬时离地的情况下将失效，而车轮受到冲击或瞬时离地并不一定会发生侧翻。例如车辆在转向时，外侧轮胎碾压到障碍物反而会使车辆回正，经过训练的特技驾驶员可以长时间保持单侧车轮离地。因此，对于轮胎处于非正常状态下车辆侧翻，LTR存在着严重的局限性。

由于汽车是一个高度非线性的振动系统，其动态侧翻过程比较复杂，汽车纵向速度、轮胎转角、车身俯仰以及它们之间的相互耦合等都是影响车辆侧翻的关键因素。任何以单物理量为状态变量的指标都不能够精确的反映实际侧翻特性。因此，文章首先通过建立一个保真度较高的非线性整车模型，正确反映上述关键因素的特性以及它们之间的耦合关系。然后利用能量方法进行汽车侧翻研究，通过一个包含多物理量的指标来评价侧翻稳定性，避免了对轮胎载荷变化的过分依赖，在单个或单侧车轮离地情况下算法仍然有效，可以为车辆侧翻预警提供参考。

1 车辆动力学模型

1.1 模型概述

将整车简化成如图1所示的非线性十自由度模型：簧载质量为一个绕动点自由旋转的刚体，质量为ms, 惯性张量为Is；非簧载质量为四个仅在车辆坐标系下垂向运动的刚体，质量为mui(i=1, 2, 3, 4)。十个自由度分别为：簧载质量三个方向的平动和三个轴向的转动，四个非簧载质量的垂向跳动。

轮胎模型采用2002版Pacejka魔术公式，魔术公式系数参考Adams 2013内置235/60 R16型轮胎，在组合滑移工况下，不考虑轮胎的自激振动[16]影响，四个轮胎的侧偏角度分别定义为

(1)

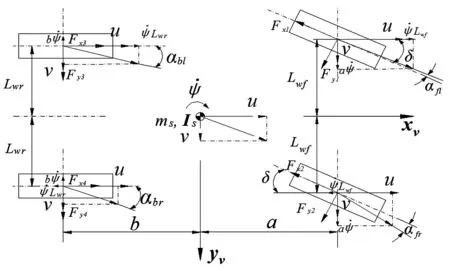
图2 轮胎受力俯视图Fig.2 Top plan view of the tire forces

1.2 运动学分析

1.2.1 坐标系及坐标转换

模型按照SAE坐标方向，定义了如图1所示的七个坐标系：一个固定地面的惯性坐标系X-Y-Z，一个固定车辆中心且相对地面做平面运动的车辆坐标系xv-yv-zv，一个固定车身的车身坐标系xb-yb-zb，四个固定非簧载质量中心的坐标系xui-yui-zui(i=1, 2, 3, 4)，车辆坐标系和车身坐标系的初始位置相同。

运动学分析采用Z-X-Y顺序的第二类欧拉旋转角，即：所有坐标系初始方向与惯性坐标系方向相同，车辆坐标系由惯性坐标系经过一次旋转得到，旋转角度为：ψg。车身坐标系由惯性系经过三次定点转动得到，旋转角度分别为：ψg,φv,θb，角标g,v,b分别为地面坐标系、车辆坐标系和车身坐标系(下同)；非簧载质量的四个坐标系方向与车辆坐标系保持一致。坐标系的转换关系为

(2)

分别表示定义eg，ev，eb，eui(i=1, 2, 3, 4)为上述七个坐标系的单位向量，则有：

(3)

1.2.2 系统的转动

车身的惯性张量在车身坐标系中才是常量，因此车身的转动需要在车身坐标系下计算，簧载质量的角速度在车身坐标系中的表达式为

(4)

同理，四个非簧载质量坐标系的角速度在车辆坐标系的表达式为

(5)

1.2.3 簧载质量质心的平动

(6)

1.2.4 非簧载质量的平动

非簧载质量质心对车辆坐标系原点的矢径分别为

(7)

式中,下标1，2，3，4 分别表示左前、右前、左后和右后四个非簧载质量(下同)，a，b，Bf，Bb，hu1～hu2，zu1～zu4的大小及含义见表1。

各质心的速度为

(8)

1.3 动力学分析

车辆模型转向时忽略阿克曼转角，假设左右轮胎的转角相同。悬架力方向始终与车辆坐标系的垂向保持一致。车辆动力学模型中，外力主要来自轮胎，其受力方向时刻随着车辆坐标系改变而改变。此外，车辆坐标系下的速度和加速度是最直观的车辆表现行为。因此，汽车的动力学方程需要转换到车辆坐标系下推导。

对于复杂运动的动力学方程，采用拉格朗日动力学方程可以避免由于计算绞约束和约束力矩带来的中间变量，从而减少计算量。

系统的动能包括平动动能和转动动能，系统的平动动能为

(9)

转动动能为

ET_r=ETb_r+ETu_r=

(10)

系统的势能包括：簧载质量和非簧载质量的重力势能；横向稳定杆、悬架弹簧和轮胎储存的弹性势能。

取汽车初始状态的是能为零，则汽车的重力势能为

EV_m=EVb_m+EVu_m=-msg(zs-hscosφcosθ)-

(11)

横向稳定杆的弹性势能为

(12)

悬架弹簧的弹性势能为

(13)

式中，zusi和zusi0分别为各悬架弹簧变形量和初始压缩量

(14)

(15)

轮胎中的弹性势能为

(16)

式中，zui为簧下质量质心位移；zgi为地面不平度；zti0为轮胎的初始压缩量，其大小为

(17)

系统的总耗散能为

(18)

为了方便受力分析，选取的广义坐标和广义外力分别为

q=[x,y,z,zu1,zu2,zu3,zu4,φ,θ,ψ]T

(19)

(20)

分别对各广义坐标求偏导可得

(i=1,2,3,…,10)

(21)

展开式(22)中的各微分方程，构成微分方程组

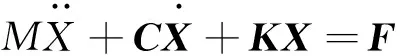
(22)

其中,

式(22)是复杂的非线性方程组，无法得到精确的解析解，需要将上述方程组转变成状态方程，使用数值积分方法进行求解

(23)

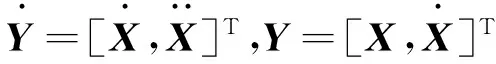
2 整车试验及模型验证

为了验证整车动力学模型的正确性，需要对同一车辆在相同工况下进行仿真实验和实车实验对比分析。车辆模型以转向盘转角(轮胎转角)和车速为输入，通过在MATLAB中利用经典四阶Runge-Kutta方法得到非线性方程组的数值解。模型仿真时以车辆实测转向盘转角和实测车速作为输入信号。

2.1 整车试验

蛇形行驶试验，是测定汽车操纵稳定性的一种经典试验方法，也是操纵稳定性试验方法国家标准中的重要组成部分，它可以评价汽车的操纵性、转向力大小、侧倾程度和避免事故的能力。双移线试验，是国际上广泛采用的测定操稳性的试验手段，它可以模拟车辆在高速避障时的车辆操纵性和转向稳定性。

为了客观和综合地验证模型的正确性，本文选用如图3所示的军用SUV进行仿真和试验。分别参照国家标准GB/T 6323—2014《汽车操稳性试验方法》[17]和国际标准ISO 3888-1：1999《小型客车急速变道试验》[18]制定试验方案，并于国家试验场进行试验。

图3 试验汽车Fig.3 The test vehicle

试验系统组成如图4所示，主要包含:便携式cRIO9025-NI(9234)采集系统、装有LabVIEW的笔记本电脑、测速仪、转向盘转角测量仪、五个传感器和电源箱。五个传感器分别为：一个低频加速度传感器(PCB-3711B112G, 2 g, 402.1 mV/g)和四个LVDT(TRANS-TEK 0246-00005 B-13, -5V～5V, V×108/8 mm)。加速度传感器通过胶水固结在一个L型的钢板上，钢板固定在车厢的质心位置处，用来测量侧向加速度；一对LVDT分别安装前轴减震器上，用80 mm抱箍固定在减震器上；另一对LVDT安装在后轴，上支架在车身钻孔做L行的支架，下支架用120 mm抱箍固定，两对LVDT用来测量悬架动行程并转化为车身侧倾角；在不影响驾驶员正常驾驶汽车的前提下，将转向盘转角测量仪固定在转向盘上。

图4 试验系统组成Fig.4 The constitute of test system

蛇形试验和双移线试验均以60 km/h的车速进行，标桩及轨迹如图5和图6所示。试验过程中记录每个传感器的采集的数据并保存。

图5 蛇形试验布桩及轨迹(m)Fig.5 Cones and tracks of the slalom test(m)

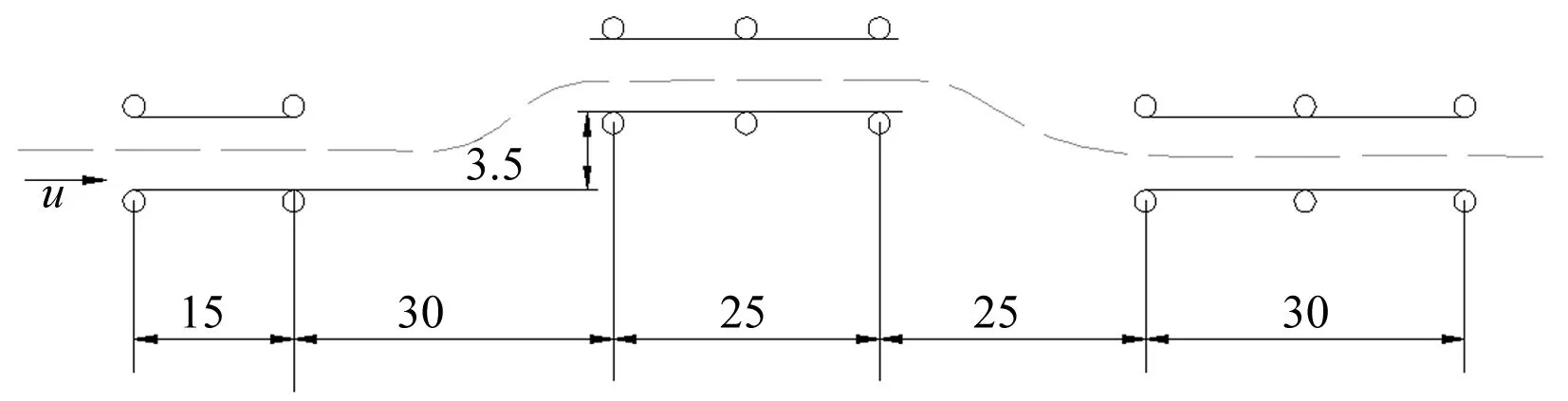
图6 双移线试验布桩及轨迹(m)Fig.6 Cones and tracks of the lane-change test(m)

2.2 模型仿真及验证

通过测量以及参数识别的方法获得车辆参数如表1所示。

表1 模型主要参数及符号说明Tab.1 Model parameters and symbol description

将参数输入到模型中，将测得车速和转向盘输入经滤波及拟合以后作为模型的输入信号，转向盘和车速输入信号如图7和8所示。

2.3 数据分析及模型验证

将蛇形试验和双移线试验测得的数据经过截断和滤波，分别与仿真得到的数据进行对比。蛇形试验的数据对比如图9和图10所示；双移线试验数据对比如图11和图12所示。

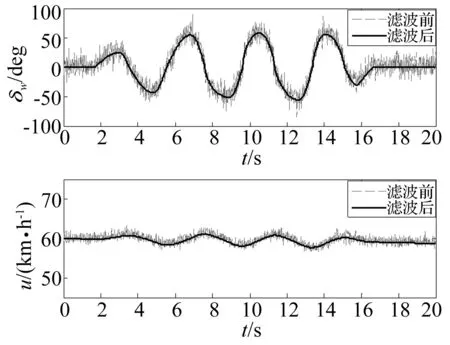
图7 蛇形试验车速和转向盘输入Fig.7 Velocity and wheel steer of slalom test

图8 双移线试验车速和转向盘输入Fig.8 Velocity and wheel steer oflane-change test

图9 蛇形试验侧倾角对比Fig.9 Comparison of roll angle in slalom test

图10 蛇形试验侧向加速度对比Fig.10 Comparison of lateral acceleration in slalom test

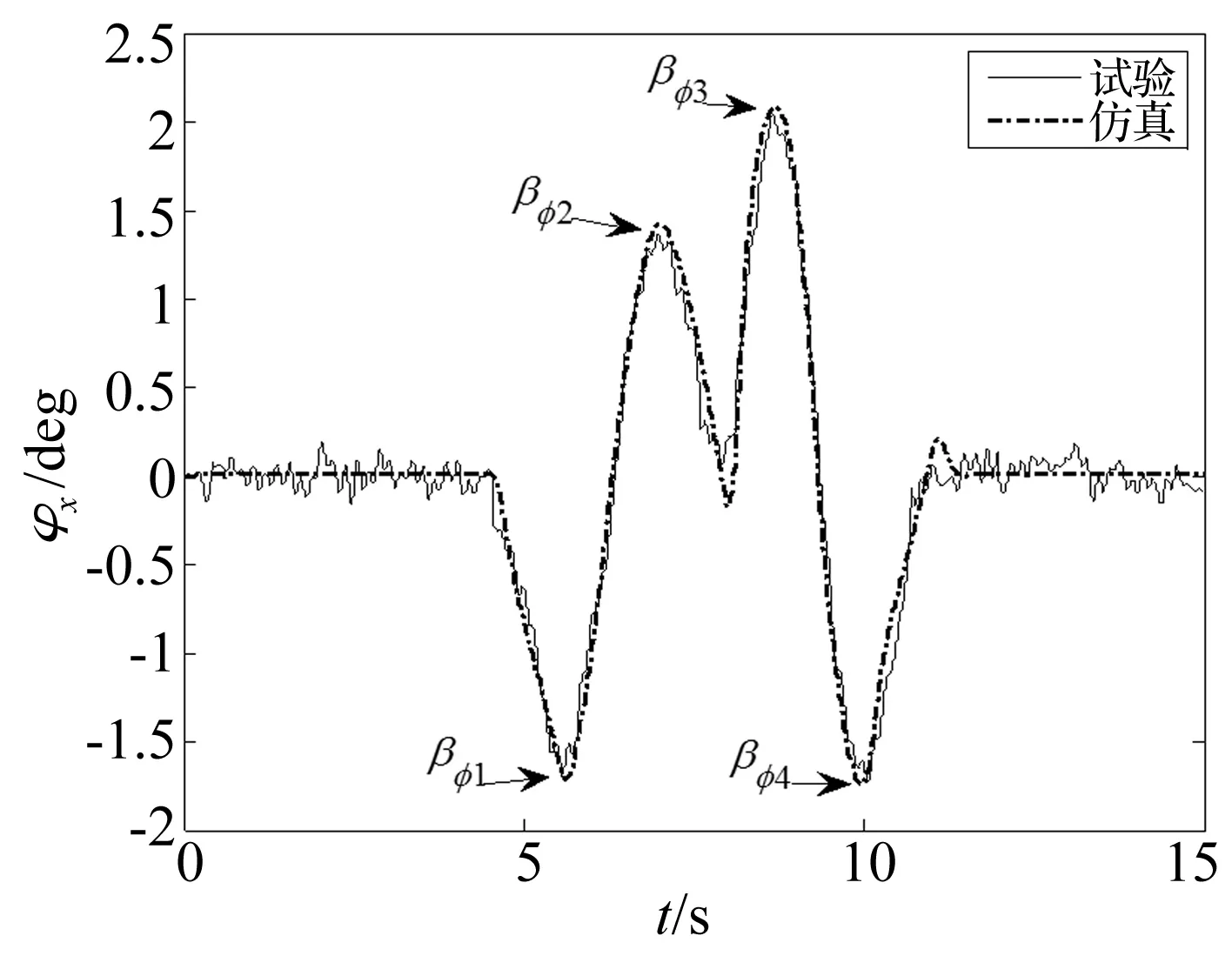
图11 双移线试验侧倾角对比Fig.11 Comparison of roll angle in lane-change test

图12 双移线试验侧向加速度对比Fig.12 Comparison of lateral acceleration in lane-change test

通过对比可知，两种试验工况下，仿真得到的侧倾角和侧向加速度最大值都与试验测得的数据存在一些偏差，其统计结果记录在表2和表3中。

表2 蛇形试验偏差统计Tab.2 Deviation statistics of slalom test

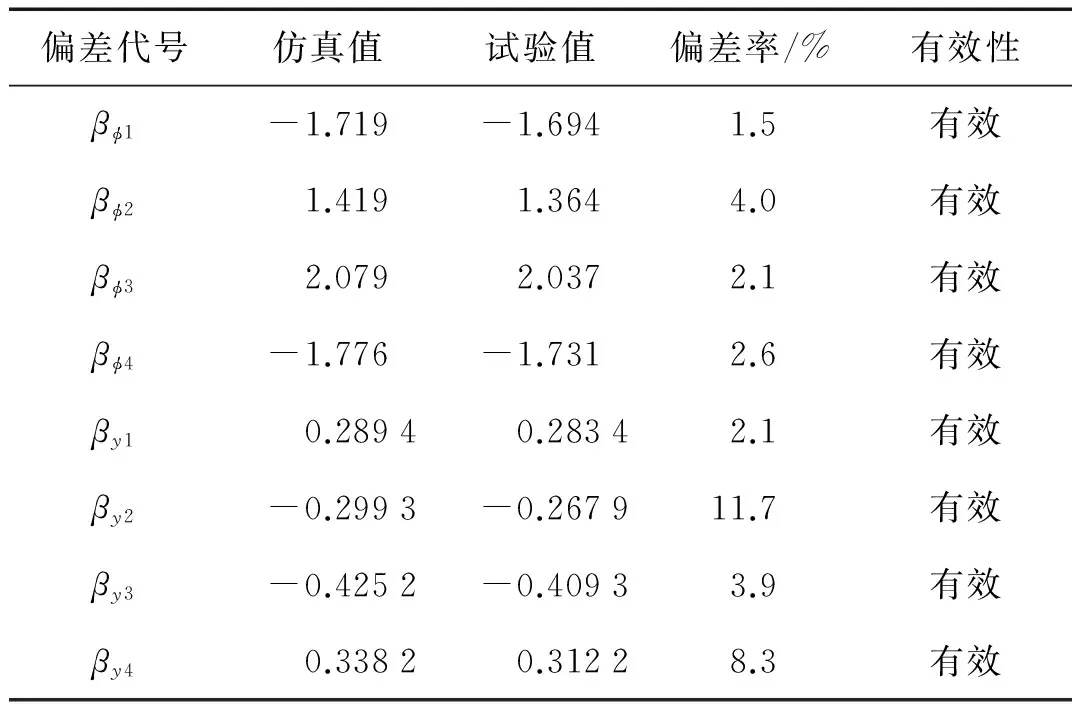
表3 双移线试验偏差统计Tab.3 Deviation statistics of lane-change test

由表2和表3数据可知，仿真得到的车身侧倾角和侧向加速度数据整体上比试验测得的数据偏大。这是由于整车试验中，测得的LVDT数据是车身相对与车轴的位移变化，忽略了轮胎变形引起的侧倾角度；而加速度传感器始终与车身固结，其角度会随着车身侧倾角变化而变化，测得的加速度值是侧向加速度的分量。综上考虑，试验数据相对仿真数据可以存在适当偏差。分析数据可知，αφ1，αφ8，αy1，αy2，和αy8的偏差率相对较大。根据国标蛇形试验的数据处理方法，车辆在通过第一个标桩以后，车辆才处于蛇形稳定转向状态，试验数据才有效，也即αφ3～αφ7和αy3～αy7为有效值，故模型与仿真的偏差率只考虑有效数据的平均偏差，两组试验数据和仿真数据对比的整体有效偏差率在10%以下。仿真与实验的对比分析验证了模型的有效性和准确性，说明可以利用该模型进行后续的侧翻稳定性研究。

3 侧翻研究的能量方法

3.1 侧翻与能量

只考虑侧向运动的汽车动力学模型可以简化为如图13所示的振动系统：底座分为质量相等的两部分，质量为mu；簧上部分可以绕O点旋转，O点可以在竖直的滑轨内上下移动，簧上质量为ms，绕O点转动惯量为Is，质心到O点的距离为hs；弹簧的质量不计，刚度为ks；阻尼器质量不计，阻尼大小为cs，模型中各参数的大小详见表4。

(24)

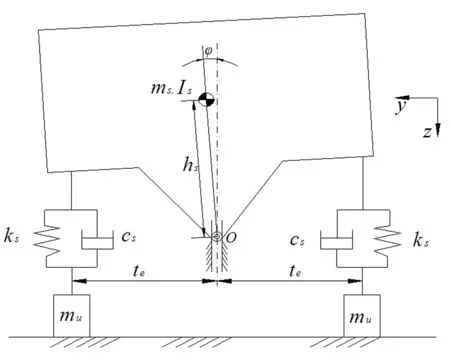
图13 汽车侧倾运动简图Fig.13 Kinematic sketch of vehicle rolling model

参数数值簧载质量ms/kg500簧下质量mu/kg50簧上质量侧倾转动惯量Is/(kg·m-2)240等效悬架宽度te/mm400侧倾力臂长度hs/mm450弹簧刚度ks/(N·mm-1)30阻尼cs/(N·s·m-1)1800

在平衡位置，给簧上质量一个初(角)速度，假设地面可以提供足够大的摩擦力，根据弹簧的变形量可以判断出簧下质量的受力状态。当初速度比较大时，系统的动能比较大，簧上质量能够达到的侧倾角就比较大。当簧上质量的初动能(初速度)足够大时，弹簧形变量足够大，非簧载质量则会被提起。

取图中右侧簧下质量进行受力分析，地面对簧下质量的支持力为

FN=mug-Fs

(25)

式中,Fs为弹簧对非簧载质量的拉力，其大小为

Fs=-ks(z0+zs-teφ)

(26)

在不同的初始角速度和初始压缩角度下，系统的总机械能和地面对非簧载质量支持力的变化状况如图14和图15所示：在振幅最大时，地面对非簧载质量的支持力最小。当系统的机械能达到一定上限时，地面对非簧载质量的最小支持力变为零，负值则意味着非簧载质量离地。随着系统振动过程的进行，系统的总能量逐渐降低，地面对非簧载质量的支持力趋于稳定。

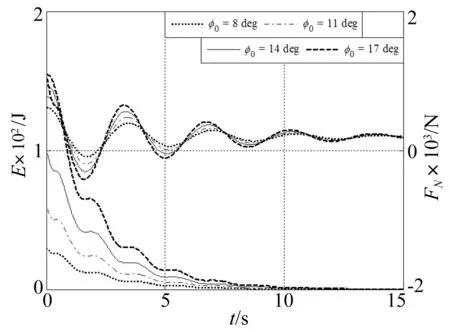
图14 侧翻能量和地面支撑力与初始压缩角的关系Fig.14 Relation respectively between E, FN and φ0

图15 侧翻能量和地面支撑力与初始角速度的关系Fig.15 Relation respectively between E, FN and ω0

根据图14和图15中各曲线的对比，当ω0>10°时，非簧载质量在系统振动的初始时刻对地面的压力并不为零，但是随着振动过程的进行，簧下质量最终会被弹簧提起，并离开地面。此时若以轮胎对地面的压力大小作为侧翻的评价指标，将得出错误的结果，因此在此情况下，使用载荷转移作为指标是错误的。

综上可知，系统的机械能越大，非簧载质量离地的可能性则越大，系统所具有的机械能大小在一定程度上决定了车辆是否具有侧翻的可能性。而且利用系统的能量作为评价指标，可以避免依赖地面与非簧载质量之间的相互作用力，从而具有普适性。

3.2 侧翻能量阈值的定义

车辆侧翻能量阈值定义为车辆从水平状态到发生侧翻所需要的最小能量值。能量阈值大小可以通过车辆(准)静态侧翻试验来确定，例如：侧拉试验、倾斜试验台等方式测得；也可以通过测量车辆结构参数，通过计算得到。

根据缓慢倾斜试验台的原理，提升过程为准静态，可以忽略动能的变化，前后势能之差ΔEp即为车辆从静态到侧翻需要的最小能量。按照现有计算方法[19]，可以计算出模型的最大侧翻稳定角。根据最大侧翻稳定角计算出车辆簧载质量和非簧载质量质心的高度变化，即可得到ΔEp。

将上述方法计算出的势能之差作为侧翻能量阈值时，忽略了轮胎变形对非簧载质量质心高度和整车侧倾的影响和悬架变形侧倾引起的簧载质量质心高度变化。能量阈值是能量法最关键的基本参数，能量阈值大小设置需合理，为了减少上述因素对侧翻能量阈值的影响，引入阈值稳定系数λet，其大小由轮胎刚度决定，能量阈值定义为

Et=λetΔEp

(27)

3.3 车辆实时侧翻能量计算

3.3.1 虚拟侧翻坐标系的定义

在行驶过程中，车辆作为一个整体，具有六个自由度，且每个自由度都有运动。但车辆的侧翻只与车辆的侧向运动和侧倾运动有直接关系。在不转向的情况下，无论车速多快，车辆都不会发生侧翻。利用一般坐标系中的车辆速度计算的车辆动能，会随着纵向车速、横摆角速度和俯仰角速度的变化而产生不可预测的误差。

为减少除了侧向速度和侧倾角速度以外的速度造成干扰，需要建立一个新的坐标系xe-ye-ze。该坐标系具有与车辆坐标系相同的纵向速度和横摆角速度，同时又与车身坐标系具有相同的俯仰角速度。则车辆在此坐标系下只具有侧向速度和侧倾角速度的分量，这也跟乘员在车辆上的直观感受相符。

3.3.2 侧翻能量计算

广义上来讲，车辆所处的姿态和本身的运动决定了车辆的能量大小，姿态与势能相关，运动与动能相关。在虚拟坐标系中，车辆亦同时具有动能和势能。动能包括整车的平动动能和簧载质量的转动动能，势能为车辆重力势能和悬架变形储存的势能，则总能量为

(28)

(29)

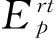
(30)

3.4 能量稳定指标

车辆是一个复杂的非线性系统，不同方向的运动相互影响。例如，车辆纵向运动不会直接导致车辆的侧翻，但车辆的纵向运动与横向运动通过转向系统耦合在一起，这使得车辆在转弯时纵向的平动动能转化为侧翻的能量。所以，能量稳定指标需要同时考虑车速和车轮转角的影响。

在实际行驶中，车辆发生侧倾实质上是车辆绕外侧轮胎接地点转动，质心升高，动能转化为势能的过程。在此过程中，部分动能还会通过悬架系统的减振阻尼消耗，且侧倾速度越快，消耗的能量就越多。综合考虑上述影响因素，定义一个新的车辆侧翻能量稳定综合评价指标：

(31)

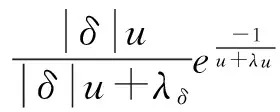
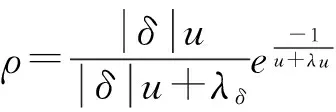
4 能量方法验证

为了验证能量方法及稳定指标的正确性，需要利用现有的侧翻指标进行验证，本文选用广泛采用的LTR因子作为对比进行验证。

由于能量稳定指标恒为正值，故需要对LTR取绝对值改为：

(32)

在MATLAB中模拟多种工况下的车辆运行状态，分别利用两种指标进行判断和对比。

4.1 转向缓慢增加工况

转向盘稳定增加工况是指方向盘随着时间不断增大，直到车辆发生侧翻的过程。该工况过程简单，结果也最直观。试验车速设定为60 km/h，转向盘输入信号如图16所示。

图16 转向缓慢增加工况输入Fig.16 Slowly-increasing input

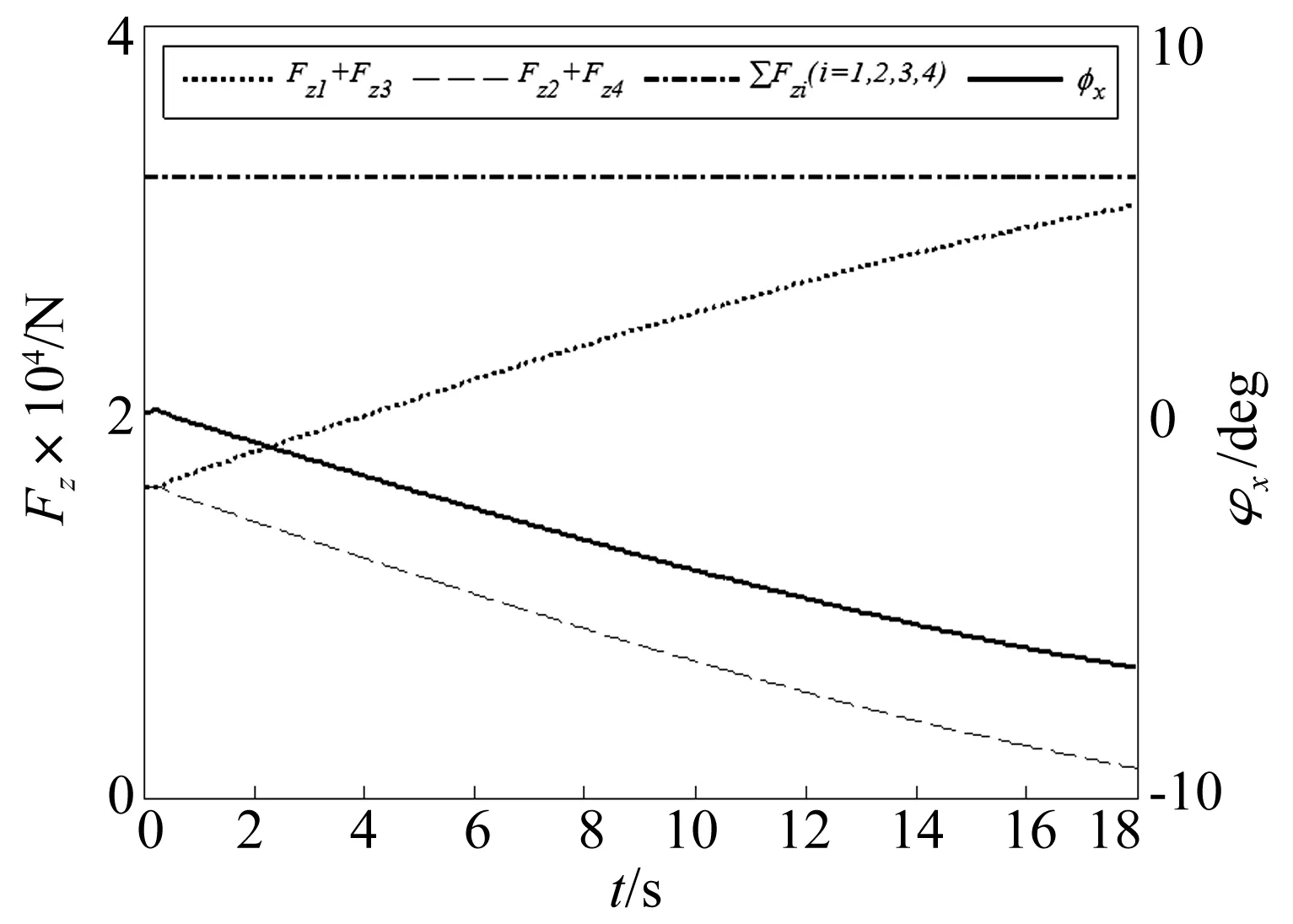
图17 转向缓慢增加工况:轮胎压力与侧倾角变化Fig.17 Slowly-increasing: tire force & roll angle

图18 转向缓慢增加工况:能量与侧倾角变化Fig.18 Slowly-increasing: energy & roll angle

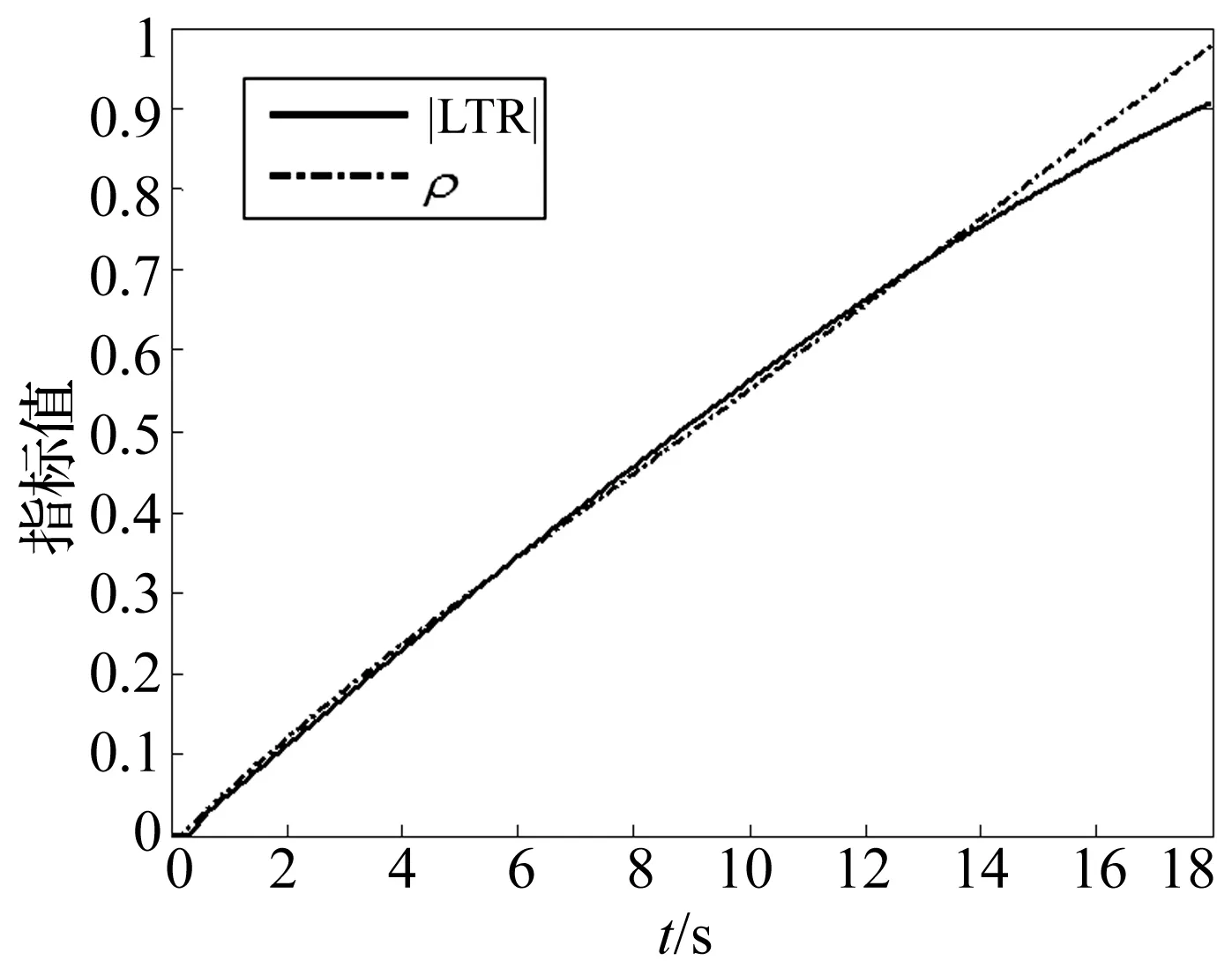
图19 转向缓慢增加工况: |LTR|与ρ指标对比Fig.19 Slowly-increasing: the comparison of |LTR| & ρ

对比图18与图19可知，在小转角时，车辆侧翻能量值与能量阈值比值较小，将会导致ρ偏小。但由于算式中第二项包含车速-转向干扰系数，使ρ偏小的情况得到了较好的修正。

由图19 |LTR|与ρ的对比可知，|LTR|与ρ在小转角时的重合度较高；在大转角时，|LTR|的变化率变小，ρ保持较高的增长率；说明ρ在车辆接近侧翻时的敏感性比|LTR|高。

4.2 正弦扫描工况

转向盘正弦扫描输入工况时，车辆近似于蛇形试验，模拟车辆连续大角度转弯时的工况。输入信号如图20所示。

图20 转向盘正弦扫描输入Fig.20 Sine swept: steering wheel input

由图20～图23可知，在正弦扫描工况下，轮胎压力值与实时侧翻能量值呈正弦变化，|LTR|值与ρ值保持较高的一致性。

图21 正弦扫描工况:轮胎压力与侧倾角变化Fig.21 Sine swept: tire forces & roll angle

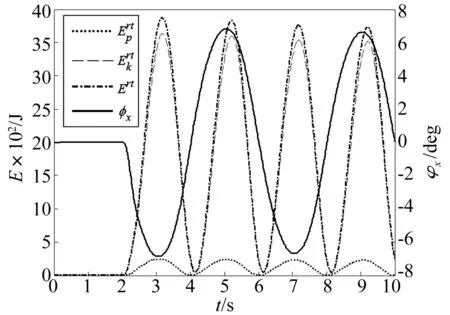
图22 正弦扫描工况: 侧翻能量与侧倾角变化Fig.22 Sine swept: rollover energy & roll angle

图23 正弦扫描工况: |LTR|与ρ指标对比Fig.23 Sine swept:the comparison of |LTR| & ρ

4.3 路面脉冲激励工况

在转向稳定增加输入的情况下，对车辆外侧车轮进行脉冲激励，模拟车辆转弯过程中受到路面散落的石头冲击，路面输入信号如图24所示。

图24 路面脉冲工况: 轮胎输入Fig.24 Ground impulse:tire input

图25 路面脉冲工况: 轮胎受力与侧倾角Fig.25 Ground impulse: tire forces & roll angle

对比图25和图26可知，转向中的车辆外侧车轮受到冲击，两侧车轮的压力同时增加；车辆的侧翻能量减小；车身侧倾角变小，车身具有回正趋势。

由图27可知，在外车轮胎脉冲激励下，|LTR|值发生突变，瞬时值由0.661突变到1.268；ρ值则发生较小的变化，从0.655降低到0.547。而实际车辆在转弯时，外侧车轮受到地面冲击，往往使车辆侧倾趋势得到遏制，故ρ值的变化更加符合实际情况。

通过以上工况的仿真结果，证明能量法可以满足传统LTR算法的应用范围，还可以在一些LTR算法失效的情况下仍然适用。

图26 路面脉冲工况: 能量与侧倾角Fig.26 Ground impulse: energy & roll angle

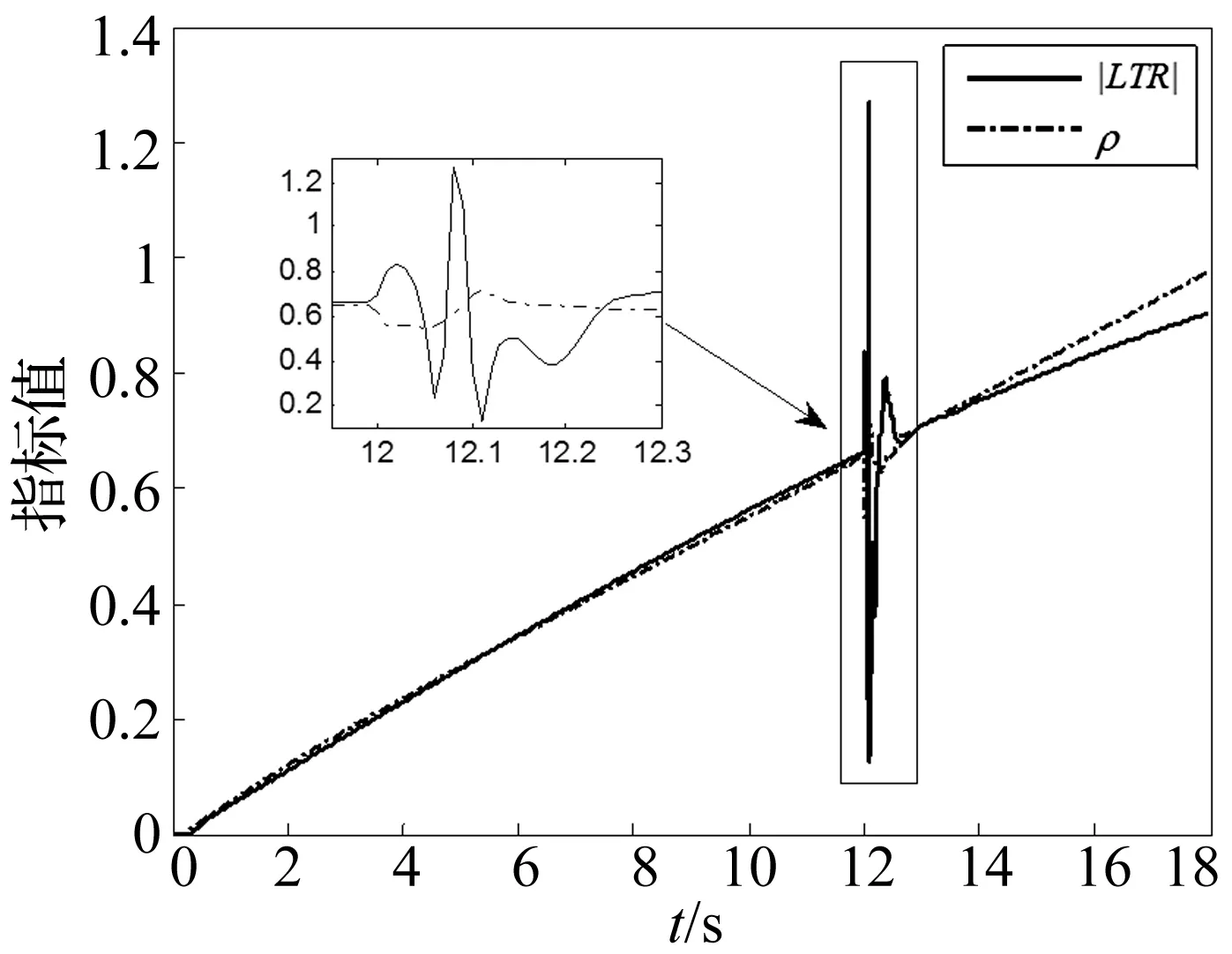
图27 路面脉冲工况: |LTR|与ρ值对比Fig.27 Ground impulse: the comparison of |LTR|& ρ

5 结 论

本文基于能量方法对车辆的侧翻稳定性进行了研究，详细推导并建立了复杂的非线性整车模型，分别按照国家标准和国际标准进行了实车试验。根据实车的参数，在不同试验工况下，对模型进行了仿真，将试验数据与仿真结果进行对比，两者吻合程度较高，验证了模型的正确性。

在能量方法的基础上，推导并提出了实时能量储备系数和车速-转向干扰系数的概念，进行了详细的讨论。提出了车辆侧翻能量稳定指标的概念，并给出了能量稳定指标的算法。通过多工况下的模型仿真，对比横向载荷转移率|LTR|和侧翻能量稳定指标ρ的吻合程度，验证了能量方法的正确性。通过模拟车辆转弯受到冲击的工况，验证了横向载荷转移率的局限性和能量法的适用性，证明能量法的使用范围更广泛。

[1] National Highway Traffic Safety Administration. Traffic safety facts 2013: a compilation of motor vehicle crash data from the fatality analysis reporting system and the general estimates system[R]. Washington DC: NHTSA，2013．

[2] GILLESPIE T D. Fundamentals of vehicle dynamics [M]. New York：SAE International, 1992.

[3] 祝军, 李一兵. 汽车侧翻和滚翻事故建模研究[J]. 汽车工程，2006，28(3)：254-258. ZHU Jun, LI Yibing. A research on the modeling for vehicle rollover and turnover accident[J]. Automotive Engineering, 2006, 28(3): 254-258.

[4] RAKHJA S, PICHE A. Development of directional stability criteria for an early warning safety device [R]. SAE Paper, 1990:902265.

[5] TRENT V, GREENE M. A genetic algorithm predictor for vehicle rollover[R]. IECON02, IEEE 28th Annual Conference, 2002.

[6] CHEN B, PENG H. Differential-braking-based rollover prevention for sport utility vehicles with human-in-the-loop evaluations[J]. Vehicle System Dynamics, 2001, 36(4/5): 359-389.

[7] PRESTON-THOMAS J, WOODROOFFE J H F. A feasibility study of a rollover warning device for heavy trucks[R]. Transport Canada Publication, 1990.

[8] DAHMANI H, CHADLI M, RABHI A, et al. Vehicle dynamic estimation with road bank angle consideration for rollover detection: theoretical and experimental studies[J]. Vehicle System Dynamics, 2013, 51(12): 1853-1871.

[9] ZHANG Nong, DONG Guangming, DU Haiping. Investigation into untripped rollover of light vehicles in the modified fishhook and the sinemaneuvers, part I: vehicle modelling, roll and yaw instability [J]. Vehicle System Dynamics, 2008, 46(4): 271-293.

[10] CHOI S B. Practical vehicle rollover avoidance control using energy method[J]. Vehicle System Dynamics, 2008, 46(4): 323-337.

[11] ROSE N A, FENTON S J, BEAUCHAMP G, et al. Analysis of vehicle-to-ground impacts during a rollover with an impulse-momentum impact model[C]//Detroit：SAE 2008 World Congress,2008.

[12] VERMA M K, GILLESPIE T D. Roll dynamics of commercial vehicles [J]. Vehicle System Dynamics, 2007, 9(1): 11-17.

[13] CHEN B C, PENG H. Rollover warning for articulated heavy vehicles based on a time-to-rollover metric [J]. ASME Journal of Dynamic Systems, Measurement and Control, 2005, 127(3), 406-414.

[14] WU Xinye, GE Xiaohong, HUANG Hongwu. Study on vehicle rollover avoidance[C]// 2010 International Conference on Measuring Technology and Mechatronics Automation,2010.

[15] 金智林, 翁建生, 胡海岩. 汽车侧翻预警及防侧翻控制[J]. 动力学与控制学报, 2007, 5(4): 365-369. JIN Zhilin, WENG Jiansheng, HU Haiyan. Rollover warning and anti-rollover ontrol for automobile[J]. Journal of Dynamics and Control, 2007, 5(4): 365-369.

[16] 左曙光，张浩鹏，赵愿玲,等. 汽车驱动轮与从动轮胎面自激振动对比研究[J]. 振动与冲击, 2014, 33(19): 17-21. ZUO Shuguang, ZHANG Haopeng, ZHAO Yuanling, et al. Tread self-excited vibration of a car’s driving wheel and driven wheel[J]. Journal of Vibration and Shock, 2014, 33(19): 17-21.

[17] 汽车操纵稳定性试验方法: GB/T 6323—2014 [S].中国国家标准化管理委员会，2014.

[18] Passenger cars-test track for a severe lane-change manoeuvre-part 1: double lane-change:ISO 3888-1[S]. Britsh: ISO, 1999.

[19] 陈耀明，张满良. 汽车静态侧翻稳定角的计算方法[J].汽车技术, 1994(4): 6-11. CHEN Yaoming, ZHANG Manliang. A method of calculating the steady-state limit angle for vehicle[J]. Automobile Technology, 1994(4): 6-11.

A study on vehicle rollover-stability dynamics based on the energy approach

HUANG Mingliang1, ZHENG Minyi2, ZHANG Bangji1, ZHANG Nong2, CHEN Shengzhao1

(1. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China;2. School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei 230009, China)

The energy approach was applied to study the vehicle rollover-stability. A new comprehensive evaluation method for vehicle rollover-stability was proposed. In order to study the methodology, a 10-DOF vehicle model with nonlinear characteristics was presented. The comparison of vehicle road test and simulations with vehicle model verifies that the model is correct. The rollover-stability index was provided: By calculating the ratio of real-time energy reserve and rollover energy threshold, the rollover energy reserve coefficient (RERC) could be deduced. And the velocity-steering interference coefficient (VSIC) was defined by integrating the vehicle velocity and the steering angle. After then, the comprehensive evaluation index of vehicle rollover stability, which contains the vehicle velocity, roll angle velocity, roll angle, and tire steering angle was established. Furthermore, the presented method was compared with the other vehicle rollover-stability evaluation methods by different situation simulation experiments. The result shows that the presented method is correct and applicable.

rollover-stability; dynamic model; energy threshold; energy stability index

国家自然科学基金项目(51175157)

2016-03-17 修改稿收到日期：2016-05-19

黄明亮 男，硕士生，1990年4月生

张农 男，教授,博士生导师，1959年6月生

U461

A

10.13465/j.cnki.jvs.2016.24.027