地铁列车出、进站加、减速的轴向激励引起出平面振动
2017-01-06陈文化
张 谦, 陈文化
(北京交通大学 土木工程学院,北京 100044)
地铁列车出、进站加、减速的轴向激励引起出平面振动
张 谦, 陈文化
(北京交通大学 土木工程学院,北京 100044)
地铁列车出、进站时引起的地层波动较为复杂而丰富,主要由于列车加、减速引起的振动特性非常特殊,尤其是地铁列车轴向激励作用下的出平面波源特性。按照波函数展开法和镜像原理,建立隧道壁上的柱面波表达式,再利用Graf加法公式和贝塞尔函数公式,推导轴向激励作用下的出平面波的振动响应解析解。将轴向激励看作是沿列车行驶方向变化的情况,假定出、进站下不同的激励模式,基于上述理论和假设,重点研究出、进站两种情况的波动差异,分别分析了地铁列车运行加速度和速度、土层模量、隧道尺寸和埋深等因素对振动反应的影响,计算发现出站过程振动更大,列车越靠近停车站,轴向振动越大,且受到参数变化的影响也越明显。
地铁地基;进(出)站;轴向激励;出平面波;参数分析
近十年来,我国城市地铁建设迅猛发展,地铁网络日益完备,极大地缓解了城市拥挤问题,但同时列车运行引起的环境振动问题也日益突出[1],围绕此问题,不少科技工作者开展积极研究工作。针对列车的振源分析以及相关的环境振动问题方面,现今大量研究是采取类似铁路振源模拟方法[2-4],分析相关轨道等结构的响应问题[5-6],没有考虑出、进站这种特殊的行驶状态引起的整体地层振动。
地铁列车运营主要有惰性状态和正常启、制动状态,只有在紧急状态下,才使用列车紧急制动模式[7-8]。紧急制动时轮轨高频摩擦,高频振动迅速被轮轨和制动材料吸收,产生巨大高频噪声和发热燃烧,较少能量以高频形式迅速在附近介质传播,一般振动时间短促,目前国内外学者针对这种瞬态响应问题做了大量研究[9-11]。然而列车出、进站是一种振动时间相对较长的变速运动过程,振动以低频形式向外传播,周围较大地层都承受相应制动力或牵引力的轴向激励作用,形成特殊的激励柱面波冲击,但这方面的研究成果很少。为此,列车出、进站作为一种特殊复杂的振动形式,其振动响应问题非常值得探讨。
本文视地铁列车进出、站引起振源以轴向激励方式作用在地铁隧道结构外缘土层上,且出平面柱面波传播,首先利用波函数展开法和镜像原理[12]求解土体内总波场,根据Graf加法公式[13-14]以及贝塞尔函数的递推公式进行简化,再根据地表及衬砌外围土层的边界条件求解二维空间下的土体动力响应解。在出、进站过程中,行驶速度相继改变[15-17],进一步推导出、进站两种不同行驶状态下的行驶速度表达式。通过算例分析,选择土层上典型点进行振动差异分析,分析列车的行驶加速度、速度、质量、土层弹性模量、泊松比、隧道埋深、半径等参数变化对进、出站引起的出平面波的振动响应的影响。
1 振源模型与动力方程
1.1 动力分析模型
在列车进、出站过程中,轴向会受到制动力或启动力的作用,这个激励过程在整个变速阶段一直存在,它是引起出平面波的主要原因。建立柱坐标系(r1,θ1,z1)下的隧道模型,图1是一个出站荷载分析模型,隧道半径为r0,轨面到地面的垂直距离为H1。

图1 地铁出(进)站时分析模型Fig.1 Vibration model of metro train leaving station
1.2 动力方程
假设土体为弹性介质,考虑问题对称性,在频域内, 地铁出(进)站的动力方程满足:
(1)
式中:k为波数,大小可以由振动频率和出平面波波速求得。
1.3 动力方程的解
满足式(1)的解的形式可以取零阶贝塞尔函数,忽略内聚项,因此柱面波势函数形式应为:
(2)
式中H0(1)(kr1)是零阶汉克斯函数,表示一道向外发散的柱面波。
考虑在半无限空间内,只存在入射和反射波。为了利用边界条件求解系数,针对出平面波的特殊性,采用镜像原理,将原来半无限空间问题转换成全无限弹性空间问题,在与地表镜像位置处构造虚拟隧道波源,采用柱坐标系(r1,θ1),(r2,θ2),如图2所示。
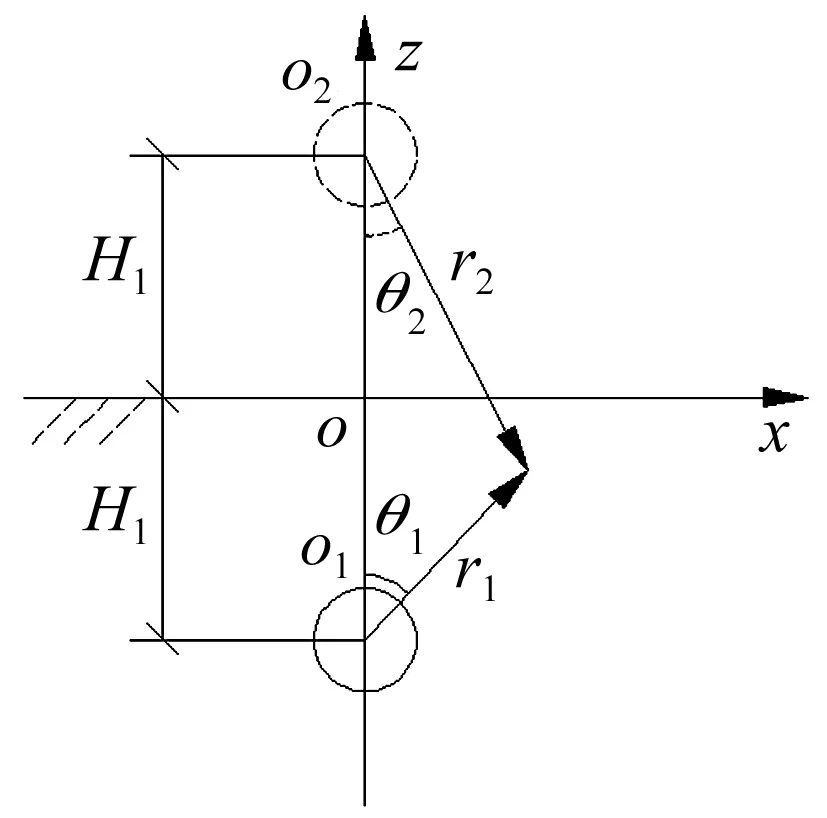
图2 出平面柱面波的镜像原理Fig.2 Mirror principium of cylindrical out-of-plane wave
根据镜像法原理,
(3)
因此半空间内的总波场函数表达式为
(4)
为便于计算,采用Graf加法公式,将(r2,θ2)坐标系里的汉克斯函数转换到(r1,θ1)坐标系下:
(5)
进一步根据贝塞尔函数递推公式,得
(6)
其中ε0=1,ε1,2,3,…,n=2。
将式(6)代入式(4)得
(7)
根据边界条件,
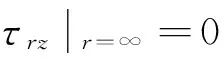
(8)
无穷远处和地表满足零应力边界,假设隧道壁的剪应力等于轴向激励沿隧道均匀分布的轴荷载,激励F大小等于行驶加速度a与车辆质量m的乘积,即r=r0处,
(9)
再由贝塞尔函数的求导递推公式,
(10)
将式(9)和(10)代入式(7)中,可得系数表达式:
(11)
将式(11)代入式(7)后,得到势函数位移表达式,进一步可以得到相应的振动速度和加速度。
2 加、减速段的激励模型
2.1 加、减速段激励模型
列车启、制动过程中,激励模式受到启、制动模式影响[15],另外轨道结构的排列、轨枕间距、轨道不平顺波长、以及行驶速度等因素都会影响振动幅值和频率[2,16-17]。
2.2 轴向激励处理方法
列车出、进站时,启、制动模式会根据线路条件、车辆原因发生变化。轴向力一般遵循增大-平稳-减小的变化过程,大小受行驶加速度、车辆质量和行驶速度等影响[15]。不考虑阻力,假设轴向力增大和减小的过程是线性变化、平稳过程是固定常数,最大牵引力、制动力与车辆质量成正比,则启、制动行驶加速度模式如图3。
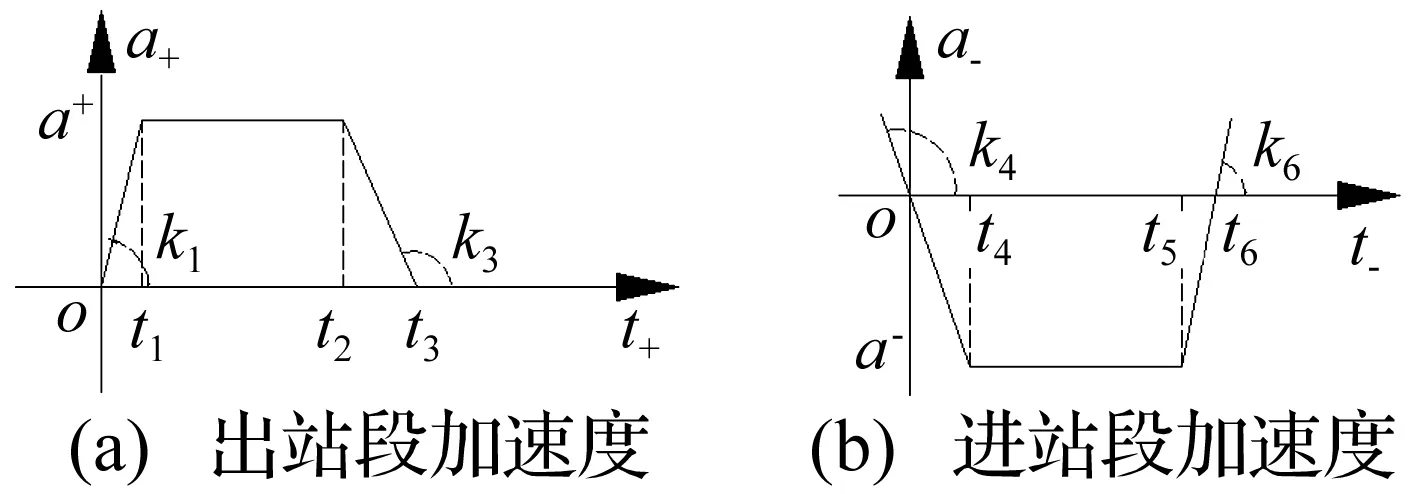
图3 列车进、出站时加速度一般模式Fig.3 Acceleration model while the metro train arriving at or leaving station
图3中,0~t1、t2~t3、0~t4、t5~t6时段都是加速度线性变化过程,k1、k3、k4、k6分别表示斜率,t1~t2和t4~t5分别是出、进站过程中加速度较稳定的阶段,a+,a-分别是出、进站平稳阶段的加速度。
在列车行驶过程中,振动频率随行驶速度的变化关系参考翟婉明的余弦函数假设[2,16-17],激扰频率按式(12),即
(12)
式中:ω为圆频率,v为行驶速度,L为轨道自身不平顺波长。列车进、出站时,振动频率还受到车辆行驶初速度、行驶时间的影响。
规定列车最大行驶速度vmax为出站末速度以及进站初速度,静止时速度为零,规定出站加速度方向为正,则进站加速度为负,出、进站行驶加速度以a+,a-表示,行驶时间以t+,t-表示,行驶速度以v+,v-表示,按行驶加速度积分可求。
初始条件满足:启动时:a+=0,v+=0;制动时:a-=0,v-=vmax,
出站阶段Ⅰ(0≤t+≤t1):
a+(t+)=k1t+,
(13)
出站阶段Ⅱ(t1≤t+≤t2):
a+(t+)=a+,
(14)
出站阶段Ⅲ(t2≤t+≤t3):
a+(t+)=k3(t+-t3),
(15)
t1和t2处满足连续条件。进站阶段同样可以按照式(13)~(15)计算,只是注意在进站阶段的速度项还要加上初速度vmax,且加速度是负值。
3 地铁振动参数分析
3.1 进、出站的出平面振动响应
以北京地铁2号线宣武门车站附近振动情况为例,分析隧道面在轴向激励下以出平面波形式传播时的振动响应情况。以隧道正上方外缘土层A点的振动响应为例(图1),选取典型算例参数见表1,注意表中弹性模量和密度是土层参数。

表1 出、进站A点振动所需参数Tab.1 Vibration parameters of point A

图4 列车进、出站A点振动加速度Fig.4 Vibration acceleration of point A while the metro train arriving at or leaving station
按三个阶段假设行驶加速度时,列车进、出站过程中,隧道正上方外缘土层A点的振动加速度见图4。出站阶段Ⅰ振动加速度波动很小,到出站阶段Ⅱ逐渐加强,最后出站阶段Ⅲ振动又减弱;进站阶段Ⅰ振动加速度明显升高,进站阶段Ⅱ振动达到峰值后逐渐减小,最后进站阶段Ⅲ振动更小。出站振动加速度振幅为1.02 m/s2,位置在出站30 s;进站振动加速度振幅为-0.86 m/s2,位置在进站5 s。
为考察进、出站引起的动力响应的差异性,分析隧道正上方外缘土层A点和斜45°方向B点(图1)的轴向振动位移规律。
列车进、出站时隧道正上方外缘土层A点和斜45°方向B点的振动位移见图5。相同行驶状态下,隧道衬砌外侧土层的两个不同方向的振幅变化规律相似,隧道顶部振幅较大,出站峰值差0.033 mm,进站峰值差0.018 mm。出站过程振动位移先增大后逐渐减小,直到出站完成,峰值发生在出站阶段Ⅰ,最大振幅0.582 mm;进站过程振动位移从零逐渐增大,峰值发生在进站阶段Ⅲ,最大振幅0.353 mm,进站引起的轴向振动位移峰值是出站的60%。

图5 出、进站引起A、B点振动位移Fig.5 Vibration displacement of different point while the metro train arriving at or leaving station
基于轴向激励模式和式(12),为进一步探讨车辆行驶状态变化以及土层特性和隧道位置尺寸变化对A点振动影响,采用控制变量法,对振动情况进行分析,注意,这里衬砌结构的尺寸、模量以及管片结构的拼装
等也会影响振动的传播,却不是本文重点,在此不予详细考虑。
3.2 列车运行参数变化时的振动响应
行驶最大加速度、最大速度的改变将影响列车的启、制动模式。
(1)运行加速度影响分析。假设行驶加速度改变只影响加速度稳定行驶段的时间,即t1~t2和t4~t5阶段,保持最大速度不变,行驶时间变化具体见表2,其余参数见表1。

表2 不同制动时间和制动加速度Tab.2 Different moving time and moving acceleration
出站末速度或进站初速度(即行驶最大速度)一定,加速度对出、进站A点的振动位移的影响见图6。列车出、进站过程中,随加速度的增大,振幅都有增加,出站阶段Ⅰ和进站阶段Ⅲ增幅明显,加速度每增加0.1 m/s2,出站振幅最大增加0.048 mm,进站振幅最大增加0.047 mm。
(2)运行最大速度影响分析。假设行驶最大行驶速度即进站初速度改变只影响进站加速度,制动模式时间保持不变,行驶加速度变化具体见表3,其余参数见表1。
进站时间一定,进站初速度对出、进站A点的振动位移的影响见图7。列车进站过程中,随初速度的增加,振幅逐渐增大,进站阶段Ⅲ增幅明显,初速度每增加5 km/h,振幅最大增加0.023 mm。
(3)列车质量影响分析。决定列车质量的因素通常有车辆类型、载客量等,选取m=2.5×103kg、m=5×103kg、m=1.5×104kg、m=5×104kg,4种质量情况,其余参数见表1。


图6 出、进站不同行驶加速度下的振动位移Fig.6Vibrationdisplacementwithdifferentmovingacceleration图7 进站不同行驶初速度下的振动位移Fig.7Vibrationdisplacementwithdifferentbrakingoriginalvelocity

表3 不同制动初速度和制动加速度Tab.3 Different braking original velocity and moving acceleration
列车质量对出站、进站A点的振动位移影响见图8。列车出、进站过程中,随着质量的增加,振幅都增大,出站阶段Ⅰ和进站阶段Ⅲ增幅明显,质量从2.5×103kg到5×104kg,出站振幅最大增加0.55 mm,进站振幅最大增加0.34 mm。
(4)轨道不平顺参数影响分析。轨道不平顺波长的不同是由于车辆本身、线路动力附加荷载、钢轨波浪形磨损等多种因素, 选取L=10 m、L=5 m、L=1 m、
L=0.1 m,4种波长情况,其余参数见表1。
轨道不平顺参数对出站、进站A点的振动位移影响见图9。不平顺波长大小对出、进站引起的振动位移有一定影响,尤其是不平顺波长比较大的情况。
3.3 土层参数变化时的振动响应
(1)土层弹性模量影响分析。选取E=5 MPa、E=15 MPa、E=25 MPa、E=35 Mpa,4种土层弹性模量,其余参数见表1。
土层弹性模量对出站、进站A点的振动位移影响见图10。列车出、进站过程中,随着土层弹性模量的增加,振幅都减小,出站阶段Ⅰ和进站阶段Ⅲ减幅明显,模量由5 MPa增加到15 MPa时,出站振幅最大减少2 mm,进站振幅最大减少1.3 mm。
(2)土层泊松比影响分析。泊松比的不同通常由于土体种类不同,选取ν=0.15、ν=0.25、ν=0.35、ν=0.45,4种泊松比情况,其余参数见表1。


图8 出、进站不同列车质量下的振动位移Fig.8Vibrationdisplacementwithdifferentmass图9 出、进站不同轨道不平顺参数下的振动位移Fig.9Vibrationdisplacementwithdifferenttrackirregularityparameters图10 出、进站不同弹性模量下的振动位移Fig.10Vibrationdisplacementwithdifferentelasticitymodulus
土层泊松比对出站、进站A点的振动位移影响见图11。列车出、进站过程中,随着土层泊松比的增加,振幅都有增大,出站阶段Ⅰ和进站阶段Ⅲ增幅明显,泊松比从0.25增加到0.35,出站最大增幅0.035 mm,进站最大增幅0.022 mm。
3.4 隧道参数变化时的振动响应
(1)隧道埋深影响分析。隧道埋深一般取轨面到地表距离,选取H1=15 m、H1=19 m、H1=23 m、H1=27 m,4种埋深情况,其余参数见表1。
隧道埋深对出站、进站A点的振动位移影响见图12。列车出、进站过程中,随着埋深的增加,振幅都有减小,埋深每增加4 m,出站最多减幅0.054 mm,进站最多减幅0.032 mm。
(2)隧道半径影响分析。选取r0=3 m、r0=4 m、r0=5 m、r0=6 m,4种半径情况,其余参数见表1。
隧道半径对出站、进站A点的振动位移影响见图13。列车出、进站过程中,随着隧道半径的增加,振幅都有减小,隧道半径增加3 m,出站最多减幅0.19 mm,进站最多减幅0.16 mm。


图11 出、进站不同泊松比下的振动位移Fig.11VibrationdisplacementwithdifferentPoisson'sratio图12 出、进站不同隧道埋深下的振动位移Fig.12Vibrationdisplacementwithdifferentburialdepth图13 出、进站不同隧道半径下的振动位移Fig.13Vibrationdisplacementwithdifferenttunnelradius
4 结 论
通过上述研究,可以得到地铁列车进、出站时轴向激励引起隧道外缘土层振动初步规律:
(1)列车出站时振动加速度峰值发生在出站30 s位置,进站时振动加速度峰值发生在进站5 s位置;出站引起振动加速度最大值比进站略大0.16 m/s2。
(2)隧道衬砌外围顶部与斜向45°方向的振幅基本一致,反应了振源假设成均匀向外传播的柱面波的合理性;列车在进、出站过程中,距离停车站越近出平面方向振动位移越大;进站引起的振动位移最大值是出站的60%。
(3)随列车出站、进站行驶加速度增加,隧道正上方外缘土层(A点)振动位移增大,出站阶段Ⅰ和进站阶段Ⅲ增幅明显。随列车进站初速度的增加,隧道正上方外缘土层振动位移增加。随列车质量增加,振幅增加,且出站增幅较大。
(4)土层弹性模量或泊松比改变对出站引起隧道正上方外缘土层振动位移影响明显,尤其泊松比引起振动位移幅值变化是进站的1.59倍。
(5)隧道埋深或隧道半径增加,隧道正上方外缘土层振动位移变小,但出站较进站大,且变化明显。
下一步进一步研究地铁列车进出站引起出平面柱面振动速度问题以及其他参数敏感性。
[1] 董霜,朱元清. 地铁振动环境及对建筑影响的研究概况[J]. 噪声与振动控制, 2003(2): 1-4. DONG Shuang, ZHU Yuanqing. A general study on vibration caused by subway and its impact for buildings [J]. Noise and Vibration Control, 2003(2): 1-4.
[2] 梁波, 罗红, 孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报, 2006, 37(1): 89-94. LIANG Bo, LUO Hong, SUN Changxin. Simulated study on vibration load of high seed railway [J]. Journal of the China Railway Society, 2006, 37(1): 89-94.
[3] MINO G D, GIUNTA M, LIBERTO C M D. Assessing the open trenches in screening railway ground-borne vibrations by means of artificial neural network [J]. Advances in Acoustics and Vibration, 2009,2009:942787.
[4] 张玉娥,白宝鸿. 地铁列车振动对隧道结构激振荷载的模拟[J].振动与冲击, 2000, 19(3): 68-70. ZHANG Yu’e, BAI Baohong. The method of identifying train vibration load acting on subway tunnel structure [J]. Journal of Vibration and Shock, 2000, 19(3): 68-70.
[5] 王少钦,夏禾,郭薇薇,等. 变速移动荷载作用下简支梁桥的动力响应及共振分析[J]. 振动与冲击, 2010, 29(2): 26-30. WANG Shaoqin, XIA He, GUO Weiwei, et al. Dynamic response and resonance analyses for a simply-supported bridge under speed-varying loads [J]. Journal of Vibration and Shock, 2010, 29(2): 26-30.
[6] DEGRANDE G, SCHEVENELS M. Vibrations due to a test train at variable speeds in a deep bored tunnel embedded inLondon clay [J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 626-644.
[7] DE HOOP A T. The moving-load problem in soil dynamics-the vertical displacement approximation [J]. Wave Motion, 2002, 36(4): 335-346.
[8] ZAKOUT U, AKKAS N. Transient response of a cylindrical cavity with and without a bonded shell in an infinite elastic medium [J]. International Journal of Engineering Science, 1997, 35(12/13): 1203-1220.
[9] 高盟,高广运,王滢,等. 均布突加荷载作用下圆柱形衬砌振动响应的解析解[J]. 岩土工程学报, 2010, 32(2): 237-242. GAO Meng, GAO Guangyun, WANG Ying, et al. Analytical solution on dynamic response of lining subjected to sudden internal uniform loading [J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 237-242.
[10] 崔堃鹏,夏禾,夏超逸,等. 横向撞击力对铁路桥梁及行车影响的模型实验研究[J]. 振动与冲击, 2014, 33(9): 48-54. CUI Kunpeng, XIA He, XIA Chaoyi, et al. Model test for effect of lateral collision force on railway bridge and vehicle running safety [J]. Journal of Vibration and Shock, 2014, 33(9): 48-54.
[11] ZHAI Chaojiao, XIA Tangdai. Dynamic response of cylindrical cavity to anti-plane impact load by using analytical approach [J]. Journal of Central South University, 2014, 21(1): 405-415.
[12] 齐辉,折勇,赵嘉喜. 带形域内圆柱形夹杂对SH型导波的散射[J]. 振动与冲击, 2009, 28(5): 142-145. QI Hui, SHI Yong, ZHAO Jiaxi. Scattering of SH waves from a circular inclusion in an infinite strip region [J]. Journal of Vibration and Shock, 2009, 28(5): 142-145.
[13] 袁晓铭. 散射问题中柱面坐标波函数的全域变换公式[J]. 地震工程与工程振动, 2010, 30(3): 1-7. YUAN Xiaoming. A camplete-damain transform formula of cylindrical wave functions for scattering problems [J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(3): 1-7.
[14] 马宏伟,陈文化,丁曼曼. 输水隧道在P波入射时的三维地震响应研究[J]. 振动工程学报. 2014, 2(27): 96-103. MA Hongwei, CHEN Wenhua, DING Manman. Three-dimensional seismic response of convey tunnel induced by P Waves [J]. Journal of Vibration Engineering, 2014, 2(27): 96-103.
[15] 桂翔. 城市轨道交通牵引计算仿真系统的研究和开发[M]. 北京:北京交通大学, 2008.
[16] 潘昌实,李德武,谢正光. 北京地铁列车的振动对环境影响的探讨[J]. 振动与冲击, 1995,14(4): 29-34. PAN Changshi, LI Dewu, XIE Zhengguang. Vibration effects of Beijing subway traffic on the environment [J]. Journal of Vibration and Shock, 1995,14(4): 29-34.
[17] 翟婉明. 车辆-轨道耦合动力学(上册)[M]. 4版. 北京: 科学出版社, 2015: 107-119.
Out-of-plane vibration induced by axial excitation while a metro train arriving at or leaving a station
ZHANG Qian, CHEN Wenhua
(School of Civil Enginering, Beijing Jiaotong University,Beijing 100044, China)
Subsoil vibration induced by a metro train arriving at or leaving a station is special and complex. Many wave characteristics are produced by the train deceleration or acceleration process, especially the out-of-plane wave induced by the metro train axial excitation. The wave function expansion method and the mirror principium were applied to build equations on the tunnel wall. The analytical solution of the out-of-plane wave in subsoil under axial excitation conditions was obtained with the Graf addition formula and the Bessel function. The axial excitation was considered as changes along the direction of the moving train. Different excitation mode was hypothesized. Based on the above methods and assumptions, soil-vibration differences between the metro train arriving at the station and leaving the station were investigated. Some parameters such as metro train moving acceleration, speed, soil elasticity modulus, tunnel sizes and burial depth were analyzed to study this type of wave characteristics. The results show that the vibration of leaving process is larger than arriving process. The distance from the station is closer, the stronger vibration and more obvious influence of parameters.
metro subsoil; arriving at or leaving a station; axial excitation; out-of-plane wave; parameters analysis
国家自然科学基金(51178035)
2016-02-25 修改稿收到日期:2016-05-16
张谦 女,博士生,1986年生
陈文化 男,教授,博士生导师,1967年生
TU435
A
10.13465/j.cnki.jvs.2016.24.016
