航天器刚柔耦合动力学建模及热诱发动力学响应分析

孙述鹏， 王 伟， 段 枭

(湖北航天技术研究院总体设计所，武汉 430000)

航天器刚柔耦合动力学建模及热诱发动力学响应分析

孙述鹏， 王 伟， 段 枭

(湖北航天技术研究院总体设计所，武汉 430000)

针对带大型太阳能帆板的航天器，使用蜂窝板对太阳能帆板进行建模，利用哈密顿原理建立了航天器刚柔耦合动力学方程，分析了刚柔耦合非线性项及系统参数对航天器固有特性和热诱发动力学响应的影响。结果表明，系统频率随中心刚体转动惯量减小而升高，存在特定的蜂窝芯层与蜂窝板厚度比值，使系统频率最高；系统刚柔耦合非线性项不影响热诱发动力学响应中的准静态位移分量，但会使热诱发振动分量的振幅增大，振动频率发生偏移；当系统热特征时间常数的倒数和系统基频接近时，热诱发振动幅值最大。研究结果对航天器参数设计提供了理论指导。

热诱发振动；太阳能帆板；刚柔耦合；蜂窝板；柔性航天器

航天器安装有多种柔性附件，如太阳能帆板、柔性天线等，以实现不同的功能。在轨运行期间，航天器周期性地进出地球阴影，柔性附件将经历温度骤变，在结构内部产生温度梯度，导致柔性附件发生变形；如果温度梯度是时变的，则可能导致柔性附件发生振动[1]。前者导致航天器姿态指向出现偏差，后者则会引起航天器姿态抖动，二者都影响航天器的性能，甚至导致航天器结构破坏。因此，对航天器热诱动力学响应进行深入研究十分必要。

许多学者对单独的柔性附件热诱发振动进行了研究。BOLEY[2]分析了受突加热载荷作用的梁的热诱发振动，并指出：当结构的热特征时间常数与其固有振动周期数量级相同时，结构可能在热变形基础上发生热诱发振动。在此基础上，THORNTON[3]将柔性结构热诱发动态响应看做准静态热变形和热诱发振动的叠加，求解了哈勃望远镜挠性卷轴式太阳能帆板的热诱发结构响应。程乐锦等[4]发展了一种热-动力学耦合的有限元方法，求解了由薄壁杆和薄膜组成的哈勃望远镜太阳能帆板热诱发振动，并和文献的理论结果进行了对比，验证了有限元方法的正确性。孔祥宏和王志瑾提出了等效位移法，通过自编Python程序计算柔性附件有限元模型各节点的等效温度载荷，再以该载荷为激励计算结构动态响应，进而对空间站柔性太阳翼[5]及其桅杆[6]的热诱发振动进行了分析。

安装有柔性附件的航天器是一类典型的刚柔耦合系统，其运动包含了航天器整体的姿态运动和柔性附件的弹性振动。由于航天器系统总角动量守恒，因此柔性附件的变形和振动必然导致航天器姿态运动。针对一类中心刚体-柔性梁航天器系统，JOHNSTON等[7]建立了其刚柔耦合线性动力学模型，并对热-结构动力学响应进行了理论研究；LI[8]则分析了此类航天器的结构热特征时间常数对系统热诱发动态响应的影响。李伟等[9]保留柔性航天器动力学模型中的刚柔耦合非线性项，使用有限元方法分析了系统的稳定性。

航天器的太阳能帆板通常由蜂窝基板上粘贴太阳能电池片组成[10]，蜂窝基板的几何参数对航天器的模态影响十分显著，但关于太阳能帆板基板(蜂窝板)参数对航天器热诱发动力学响应的影响的相关研究，目前尚未发现有所报道。此外，虽然有文献[9]使用计入刚柔耦合非线性项的航天器动力学方程进行系统动态特性分析，但这些工作仅局限于计算响应，而未能有进一步的分析。有鉴于此，本文使用蜂窝板对太阳能帆板进行建模，利用哈密顿原理建立了航天器刚柔耦合非线性动力学方程，分析了中心刚体转动惯量和蜂窝板参数对航天器固有特性及热诱发动力学响应的影响，并对系统非线性特性进行了研究。

1 航天器模型描述

图1所示为一类典型航天器结构，由星体平台(中心刚体)和一对大型太阳能帆板组成[11]，是典型的刚柔耦合系统，航天器整体受热流S0照射。中心刚体半径为r0，转动惯量为JR；太阳能帆板长L，宽b，假定长宽比L/b较大，可用欧拉-伯努利梁建模。忽略太阳能帆板上的太阳能电池片和粘合剂的影响，仅考虑其主体结构——蜂窝基板，如图2所示。蜂窝板总厚度为2h，蜂窝芯层厚2hc，上下面板厚度均为hf。蜂窝板由铝制成，其材料密度和弹性模量分别为ρ0和E0，则上下面板的材料密度ρf和弹性模量Ef分别等于ρ0和E0；蜂窝胞元为边长lc的正六边形结构，壁厚为δc。将蜂窝芯层等效为几何参数不变的实心层，其等效材料密度ρc和弹性模量Ec可依据Gibson公式[12]得到

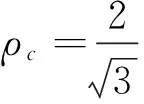
(1)

随后将蜂窝板视为三层板，使用经典层合板理论建模。

为了描述航天器姿态运动和太阳能帆板变形，建立了惯性坐标系o-XY和和随体坐标系o-xy，如图1所示。航天器在X-Y面内的姿态运动用θ表示，太阳能帆板上任意点P在随体系o-xy中的矢径为r，沿x和y的变形分别为u(x,t)和v(x,t)。

图1 航天器结构Fig.1 Spacecraft with rigid hub and flexible solar panel

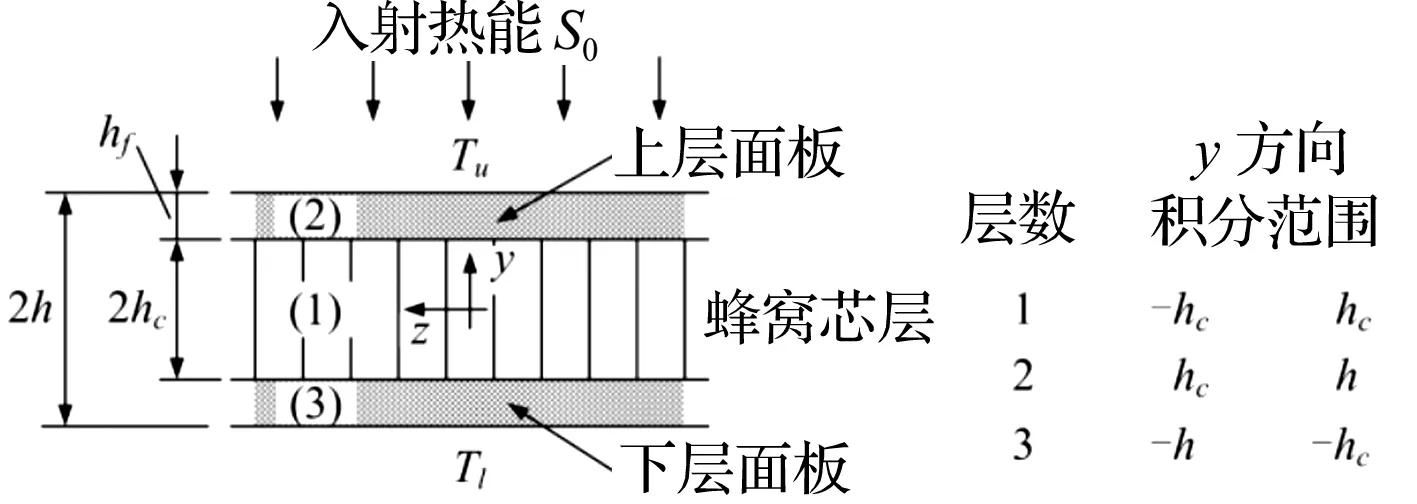
图2 太阳能帆板蜂窝基板横截面Fig.2 Cross section for the honeycomb panel of solar panel

2 航天器热诱发动力学响应分析模型

2.1 太阳能帆板热响应分析

如图1所示，太阳能帆板所受热流垂直于其未变形时的表面。对于对日定向的太阳能帆板，假定热流从零时刻开始照射，即t<0时S0=0，t≥0时S0≠0；在姿态转动和帆板振动较小时，假定结构热响应与结构变形无关；忽略太阳能帆板轴向(x方向)的温差，认为帆板仅在厚度方向(y方向，即热流入射方向)存在温度梯度[8]。

太阳能帆板热传导方程是非线性方程，不能求出解析解。对于给定边界条件的结构瞬态热响应问题，只能使用有限元方法或者有限差分法求解。然而，已有文献给出了太阳能帆板横截面温差ΔT(t)的近似解析解[7]

ΔT(t)=Tu(t)-Tl(t)=ΔTs(1-e-t/τ)

(2)

式中，Tu(t)和Tl(t)分别是蜂窝板上下面板的温度。τ是蜂窝板热特征时间常数，可由下式算出

(3)

式中c和kc分别是蜂窝芯层的比热容和导热系数。式(2)中ΔTs=Tu-Tl，是帆板横截面温差ΔT(t)的稳态值，其中Tu和Tl分别是稳态时的帆板上下表面温度，可由下面两式解出

(4)

(5)

式(4)表示稳态时帆板吸收的热和上下面板辐射的热相等，式(5)表示稳态时流过蜂窝芯层的热与下面板辐射的热相等。两式中，σ为黑体辐射系数(Stefan-Boltzmann constant)，εu和εl分别是蜂窝板上下面板的发射率，α是上面板的吸收率。

太阳能帆板横截面温差会产生热弯矩MT(t)。假定仅由蜂窝板的上下面板提供抗弯刚度[7, 13]，则MT(t)的计算表达式为

MT(t)=∫AEfαcte[T(y,t)-Tref]ydA

(6)

式中，αcte是上下面板的热膨胀系数，Tref是参考温度，积分区域A为图2中的区域(2)和(3)。将式(2)代入式(6)，进一步计算可得

(7)

2.2 航天器动力学方程

太阳能帆板上任意点P在随体系o-xy中的矢径r以及惯性系o-XY中的速度矢量v的表达式为

(8)

则航天器系统动能可表示为

(9)

航天器势能仅包含太阳能帆板的应变能。帆板蜂窝芯层和上下面板的应力-应变关系和本构关系为

εc(f)=-yc(f)v″c(f),σc=Ecεc,σf=Efεf

(10)

则系统势能可写为

(11)

由哈密顿原理

(12)

推导得到系统动力学方程如下

(13)

(14)

对应的边界条件为

(15)

式(13)～(15)中各参数为

ρ=2hcbρc+2hfbρf,

(16)

动力学方程式(13)和(14)中有下划线的项为刚柔耦合非线性项，在JOHNSTON等[1,7-8]的研究中忽略了这些非线性项，使用线性方程对航天器热诱发动力学响应进行了分析。

使用前5阶悬臂梁函数离散系统动力学方程，可得离散动力学模型

(17)

式中，M和K是5×5的矩阵，UT和FMT是5×1的列向量，其表达式为

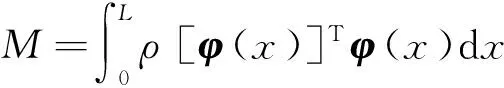
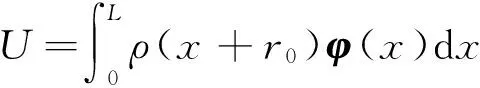
(18)

3 航天器固有特性及热诱发动力学特性

3.1 模型验证

为验证式(17)的正确性，采用孔宪仁等[14]使用的中心刚体-柔性梁模型参数，计算了系统前三阶固有频率，并与该文献中的有限元模型计算结果进行对比。从表1可知，式(17)所得系统频率与文献结果完全一致，从而验证了式(17)的正确性。

表1 中心刚体-柔性梁模型前三阶圆频率Tab.1 The first three frequencies of a hub-beam system rad/s

下面使用算例，自编MATLAB计算程序，用四阶龙格-库塔法(即MATLAB的ODE45函数)求解式(17)，分析了中心刚体转动惯量JR、蜂窝芯层高度hc等参数对航天器固有频率和热诱发振动响应的影响，算例参数如表2所示。

3.2 系统固有特性及热诱发动力学响应分析

令航天器中心刚体转动惯量JR=250rJR(1≤rJR≤100)，蜂窝芯层厚度与蜂窝板厚度比值hc/h=0～0.999 5，系统其他参数见表2。使用式(17)的线性齐次形式计算航天器整体的基频，作图3。从图中可以看出，在任一JR取值条件下，随着蜂窝芯层厚度增加(即hc/h从0增大到1)，航天器基频先缓慢增大后急剧减小，即存在一个特定的hc/h值，使航天器基频最大，这一结论与蜂窝板研究的结论相同[15]。而且，不同的JR取值，对应的使系统基频最大的hc/h的值也不同。因此，有必要针对特定的JR设计蜂窝基板的尺寸，使航天器固有频率最大。此外，还可从图3观察到，系统频率随中心刚体转动惯量JR减小而增大。

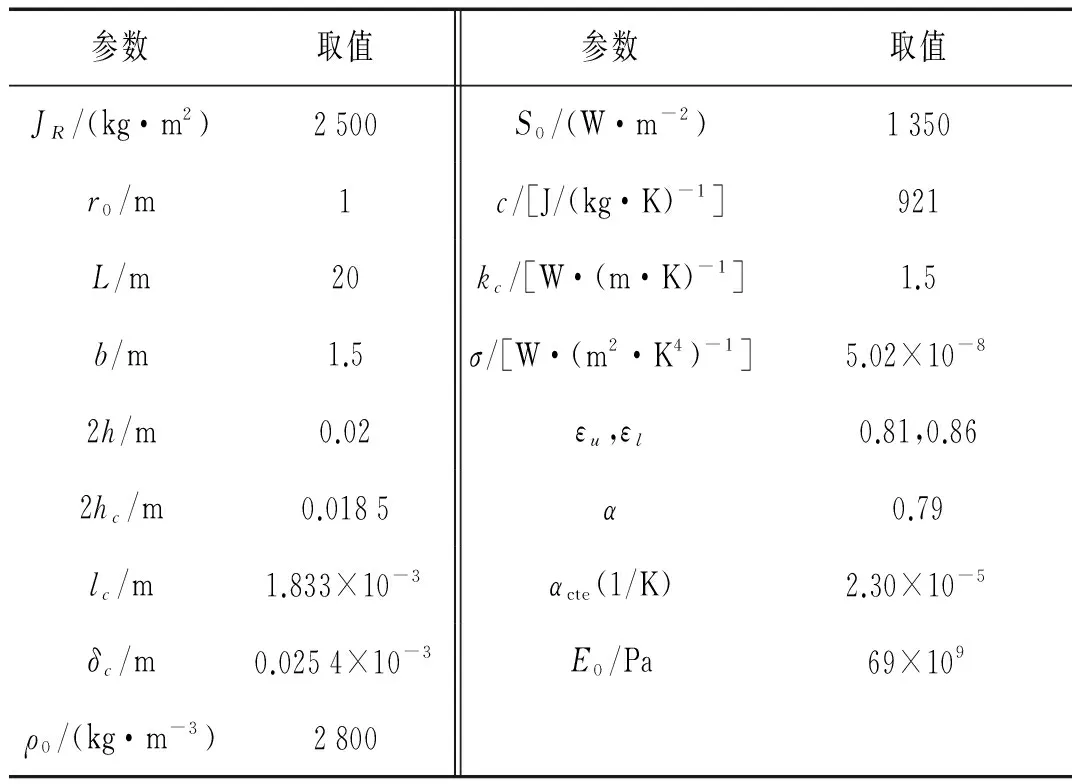
表2 航天器热诱发振动分析所用参数Tab.2 Parameters used in the thermally induced vibration analysis of a spacecraft

取表2中的航天器参数，计算无阻尼系统热诱发动力学响应，如图4所示。从中可以看出，航天器在出阴影时，受突加热流的影响，航天器太阳能帆板横截面出现时变的温度梯度，导致帆板变形，并产生振动，从而引起航天器姿态运动。当帆板横截面温度梯度趋于稳态时，航天器的动力学响应表现为准静态位移与振动的叠加。若计入结构阻尼，则图4所示动态响应中的振动部分将逐渐衰减，最后只余下准静态位移[7,9]。

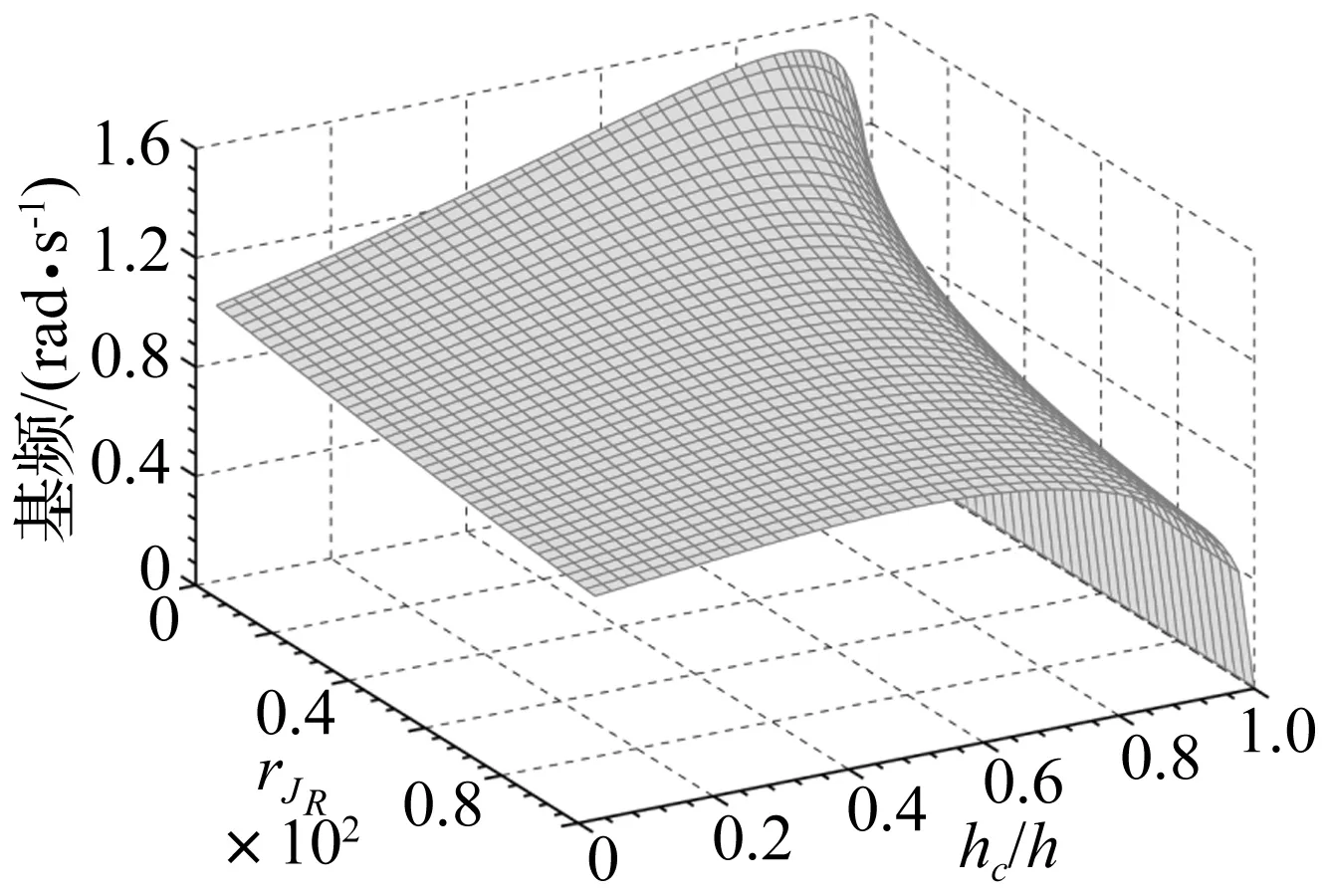
图3 航天器基频随rJR和hc/h的变化Fig.3 Variation of fundamental frequency for a spacecraft with aspect to rJR and hc/h

图4 航天器热诱发动力学响应Fig.4 Thermally induced dynamic response for a spacecraft

取JR=2 500 kgm2，分别采用式(17)的非线性和线性形式，计算参数hc/h=0～0.999 5条件下航天器的热诱发动态响应。将稳态时的姿态角θ和太阳能帆板端部位移v(L)的准静态值(用下标Q表示)及振动幅值(用下标v表示)分别取出，结果见图5。对比图5(a)和(b)可以发现，非线性模型和线性模型得出的系统稳态时准静态位移θQ和vQ(L)完全一致，这说明系统刚柔耦合非线性项不影响准静态位移。事实上，依据JOHNSTON等[1,7]的分析，受突加热流作用的航天器的准静态位移仅与MT(t)/D有关，而在hc/h=0.98附近，MT(t)/D取最大值，故此处准静态位移最大。

对比图5(c)和(d)可以看到，非线性模型计算的振动幅值与线性模型的振幅有差异，且一般情况下前者大于后者。为了进一步分析刚柔耦合非线性项的影响，分别使用非线性和线性模型计算航天器(参数见表2)热诱发动态响应，并进行频率分析，如图6所示。对比非线性模型和线性模型的结果可知，刚柔耦合非线性项使系统热诱发振动的频率成分中包含有线性系统各阶频率之外的成分。此外，hc/h分别在0.25和0.99附近取值时，会使系统热诱发振动幅值取极大值。为进一步分析其原因，采用数值的方式得出了航天器热特征时间常数的倒数1/τ与系统基频的交线，如图7所示。可以看到，当JR=2 500 kg·m2(即rJR=10)时，hc/h分别取0.36和0.99，会使1/τ与系统基频接近，导致系统热诱发振动幅值最大。进一步地，在热-结构耦合分析中，1/τ与系统基频接近会导致系统热诱发振动发散[3,8]

综合图3和图5可知，对于特定中心刚体转动惯量JR取值条件下，需要对太阳能帆板的蜂窝基板参数进行针对性设计，从而使系统频率最高，且热诱发动态响应最小。指导设计的关键参数为中心刚体转动惯量JR、蜂窝芯层与蜂窝板厚度比hc/h以及结构热特征时间常数τ。

图5 航天器热诱发运动的稳态响应随hc/h的变化趋势Fig.5Variationofsteady-statethermallyinducedresponsewithaspecttohc/h图6 姿态角振动响应的稳态频谱Fig.6Steady-statefrequencyspectrogramforthevibrationofattitudeangle

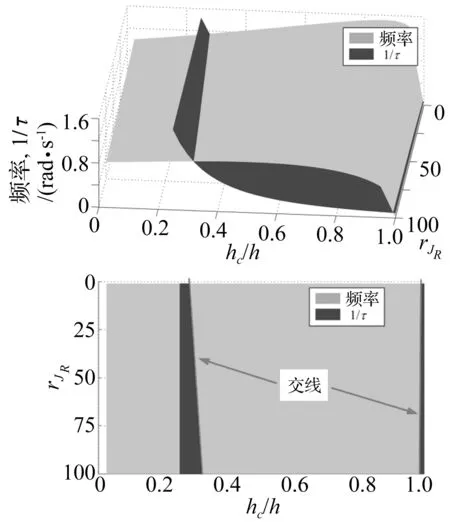
图7 航天器基频与热特征时间常数倒数的比较Fig.7 Comparison between the frequencies and 1/τ

4 结 论

本文针对带大型太阳能帆板的航天器，建立了其刚柔耦非线性动力学方程，在验证模型正确的基础上，利用具体算例分析了航天器参数对系统固有特性及热诱发动力学响应的影响，结论如下：

(1)中心刚体转动惯量越小，系统频率越高。中心刚体转动惯量取值一定时，存在特定的蜂窝芯层与蜂窝板厚度比值，使系统频率最高。

(2)航天器热诱发动力学响应包含准静态位移和热诱发振动两部分。系统刚柔耦合非线性项不影响准静态位移，但会使系统振幅增大，振动频率发生偏移。

(3)当系统热特征时间常数的倒数和系统基频接近时，热诱发振动幅值最大。

综合来看，有必要对中心刚体转动惯量、蜂窝芯层与蜂窝板厚度比值以及结构热特征时间常数进行针对性设计，使系统频率最高且热诱发动力学响应最小。

[1] JOHNSTON J D, THORNTON E A. Thermally induced dynamics of satellite solar panels[J]. Journal of Spacecraft and Rockets, 2000, 37(5): 604-613.

[2] BOLEY B A. Thermally induced vibrations of beams[J]. Journal of the Aeronautical Science, 1956, 23(2): 179-181.

[3] THORNTON E A, KIM Y A. Thermally induced bending vibrations of a flexible rolled-up solar array[J]. Journal of Spacecraft and Rockets, 1993, 30(4): 438-448.

[4] 程乐锦, 薛明德. 大型空间结构热-动力学耦合有限元分析[J]. 清华大学学报(自然科学版), 2004, 44(5): 681-684. CHENG Lejin, XUE Mingde. Coupled thermal-dynamic FEM analysis of large scale space structures [J]. Journal of Tsinghua University (Science & Technology), 2004, 44(5): 681-448.

[5] 孔祥宏, 王志瑾. 空间站柔性太阳翼热诱发振动分析[J]. 振动与冲击, 2015, 34(5): 220-227. KONG Xianghong, WANG Zhijin. Thermally induced vibration analysis of a space station’s flexible solar wing [J]. Journal of Vibration and Shock, 2015, 34(5): 220-227.

[6] 孔祥宏, 王志瑾. 空间站柔性太阳翼桅杆热诱发振动分析[J]. 上海交通大学学报, 2014, 48(8): 1103-1108. KONG Xianghong, WANG Zhijin. Thermally induced vibration of the flexible solar wing of the mast of space station [J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1103-1108.

[7] JOHNSTON J D, THORNTON E A. Thermally induced attitude dynamics of a spacecraft with a flexible appendage[J]. Journal of Guidance Control & Dynamics, 1998, 21(4): 581-587.

[8] LI L, YUAN J. Analysis and modeling of spacecraft with flexible solar panel disturbed by thermally induced motion[C]// Proceedings of the Control Conference (CCC), 2014 33rd Chinese. Nanjing, 2014: 6382-6387.

[9] 李伟, 薛明德, 向志海. 刚体-附件耦合系统热-动力学稳定性分析[J]. 浙江大学学报(工学版), 2009, 43(7): 1288-1292. LI Wei, XUE Mingde, XIANG Zhihai. Thermal-dynamic stability analysis of structural appendages attached to satellite [J]. Journal of Zhejiang University (Engineering Science), 2009, 43(7): 1288-1292.

[10] LI J, YAN S. Thermally induced vibration of composite solar array with honeycomb panels in low earth orbit[J]. Applied Thermal Engineering, 2014, 71(1): 419-432.

[11] GASBARRI P, MONTI R, SABATINI M. Very large space structures: non-linear control and robustness to structural uncertainties[J]. Acta Astronautica, 2014, 93(1): 252-265.

[12] LI J, YAN S, CAI R. Thermal analysis of composite solar array subjected to space heat flux[J]. Aerospace Science and Technology, 2013, 27(1): 84-94.

[13] 夏利娟, 金咸定, 汪庠宝. 卫星结构蜂窝夹层板的等效计算[J]. 上海交通大学学报, 2003, 37(7): 999-1001. XIA Lijuan, JIN Xianding, WANG Yangbao. Equivalent analysis of honeycomb sandwich plates for satellite structure [J]. Journal of Shanghai Jiaotong University, 2003, 37(7): 999-1001.

[14] 孔宪仁, 杨正贤, 张锦绣, 等. 刚柔耦合系统的输入成形控制[J]. 哈尔滨工业大学学报, 2011, 43(3): 7-11. KONG Xianren, YANG Zhengxian, ZHANG Jinxiu, et al. Input shaping control for rigid-flexible coupling systems [J]. Journal of Harbin Institute of Technology, 2011, 43(3): 7-11.

[15] YU S D, CLEGHORN W L. Free flexural vibration analysis of symmetric honeycomb panels[J]. Journal of Sound and Vibration, 2005, 284(1): 189-204.

Rigid-flexible couplingdynamic modelling and thermally induced vibration analysis for a flexible spacecraft

SUN Shupeng, WANG Wei, DUAN Xiao

(Institute of Overall Design, Hubei Aerospace Technology Academe, Wuhan 430000, China)

A rigid-flexible coupling dynamic model for a flexible spacecraft with large solar panels represented by honeycomb panels was established by using the Hamiltonian principle. The effects of rigid-flexible coupling nonlinear terms on the dynamic model and the parameters of the flexible spacecraft on the natural characteristics and thermally induced vibration of the system were investigated. The numeric simulation results show that the frequencies of the system increase with decreased inertia of the rigid hub of the flexible spacecraft, and there is a particular honeycomb core height to solar panel thickness ratio which corresponds to the maximum system frequency. The rigid-flexible coupling nonlinear terms do not affect the quasi-static part of the thermally induced response of the flexible spacecraft; however, they increase the amplitude of vibration part and change the system frequency. When the reciprocal of the thermal time constant of the system is close to the fundamental frequency, the amplitude of thermally induced vibration reaches maximum. The conclusions provided theoretical guidance for spacecraft design.

thermally induced vibration; solar panel; rigid-flexible coupling; honeycomb panel; flexible spacecraft

2015-09-18 修改稿收到日期：2015-12-01

孙述鹏 男，博士，工程师，1986年9月生

V414.3；V414.6

A

10.13465/j.cnki.jvs.2016.24.013