基于动力能力谱法的RC结构位移放大系数
2017-01-06陈伟宏崔双双
陈伟宏, 蒋 认, 崔双双, 吴 波
(1.福州大学 土木工程学院,福州 350108; 2.东南大学 土木工程学院,南京 210096;3.福建工程学院 土木工程学院,福州 350108)
基于动力能力谱法的RC结构位移放大系数
陈伟宏1,2, 蒋 认1, 崔双双3, 吴 波3
(1.福州大学 土木工程学院,福州 350108; 2.东南大学 土木工程学院,南京 210096;3.福建工程学院 土木工程学院,福州 350108)
结构位移放大系数是预测结构在某一地震设防水准作用下的最大弹塑性变形,从而指导结构设计的参数。我国现行抗震设计规范尚未引入结构位移放大系数。考虑6、7、8三个设防烈度,设计了3、5、8、10、12层共15个钢筋混凝土框架结构,建立其有限元模型,并采用结构振动台试验对有限元模型进行验证,进而对结构在地震作用下的反应进行分析。采用文中提出的动力能力谱方法,研究按我国抗震设计规范设计的RC框架结构在不同设防水准下的位移放大系数需求值,并与传统静力能力谱法得到的位移放大系数需求值进行对比分析。6、7、8度设防的RC框架结构的位移放大系数需求值在中震作用下分别为0.51~1.91、0.49~1.93、0.56~2.24;在大震作用下分别为1.28~4.82、1.40~4.89、1.37~5.56。中震作用下,按我国抗震设计规范设计的钢筋混凝土框架结构未发生整体屈服,表明我国抗震设计规范比较保守。
动力能力谱方法;静力能力谱方法;结构位移放大系数;需求值;RC框架结构
1985年墨西哥和1989年美国发生的地震中,很多结构由于发生相互碰撞而倒塌。如果可以对结构在大震作用下的变形进行准确预测,给出结构位移放大系数的合理取值,从而确定相邻结构间的最小距离,就能避免该类灾害的发生。
美国、欧洲和加拿大等国家的抗震设计规范中均引入了结构位移放大系数,但其取值大都由经验确定的。为了定量评价结构位移放大系数,FARAHI等[1]研究了横梁加强型人字形支撑钢结构的反应修正系数、超强系数和位移放大系数。SAMIMIFAR等[2]研究了钢筋混凝土框架结构的位移放大系数,建议钢筋混凝土框架结构位移放大系数与反应修正系数的比值最小值为1。AHMAD等[3]通过结构位移放大系数、延性系数和结构反应修正系数,研究了加固前后砌体结构的性能水平。KUYLMAZ等[4]设计并研究了72个偏心框架结构的位移放大系数,结果表明,ASCE7-10中给出的结构位移放大系数取值在预测结构层间位移角时取值不够保守,给出了结构位移放大系数的建议取值。WISNUMURTI等[5]对印尼的砖砌体结构的位移放大系数进行了研究,并给出了该结构位移放大系数的建议取值。
我国现行抗震设计规范采用的是小震弹性设计理论,无法在进行结构设计时预测结构在中震和大震作用下的弹塑性位移。童根树等[6-7]建立了等延性的位移放大系数谱,并分析了双肢剪力墙结构的位移放大系数。金双双等[8]研究了一种新型组合结构体系的结构影响系数和位移放大系数。李宇等[9]研究了地震动特性及恢复力模型动力参数对弹塑性位移谱与残余位移谱影响。陈伟宏等[10-11]研究了RC框架结构的位移放大系数能力值的取值及其变化规律。发现按我国现行抗震规范设计的RC框架结构的位移放大系数与结构反应修正系数的比值(Cd/R)介于0.8~1.2之间。我国《建筑工程抗震性态设计通则》(CECS 160—2004)提出了结构位移放大系数的概念,并根据工程经验给出了25种结构体系的位移放大系数建议值,但是尚需要对其进行深入研究。
考虑不同层数,不同设防烈度严格按中国《建筑抗震设计规范》GB 50011—2010设计15个典型钢筋混凝土框架结构,采用动力能力谱方法,研究结构在不同设防水准下的位移放大系数需求值及其变化规律,并将其分析结果与传统静力能力谱方法分析结果进行对比分析。
1 结构位移放大系数需求值概念
文中将结构位移放大系数作为结构需求。分析结构在小震、中震和大震作用下的最大反应,并得到结构位移放大系数需求值。结构位移放大系数表达式如下:
(1)
式中,Cd为结构位移放大系数,Δmax表示结构最大位移,Δd表示结构设计位移。
2 结构位移放大系数需求分析
2.1 基于静力能力谱法的位移放大系数需求分析
采用静力能力谱方法对结构位移放大系数需求值进行分析,采用ATC40的A类方法搜索目标性能点,具体步骤如下:
步骤1 采用静力分析方法,得到结构能力谱曲线即谱加速度A-谱位移D曲线。
步骤2 把规范中5%阻尼的弹性反应谱转换成A-D形式。
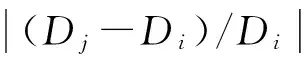
步骤4 将步骤3得到的目标位移Δmax除以结构设计位移Δd,得到结构位移放大系数需求值。
2.2 基于动力能力谱法的位移放大系数需求分析
传统的静力能力谱方法中需求谱是一条动力曲线,能力谱为一条静力曲线,性能点为此动力需求谱曲线和静力能力谱曲线叠加相交的交点,根据此性能点可得到结构在某一强度地震作用下的最大位移反应限值。
为了改善静力能力谱方法中静力能力谱与动力需求谱曲线的不协调性,文中提出了采用动力能力曲线对RC框架结构进行IDA增量动力分析。首先,每次时程分析得到的结构最大基底剪力和最大顶部位移可以在力—位移曲线上确定出一个点,将所有时程分析得到的点相连,可以得到一条基底剪力(Vb)与顶部位移(Δ)的动力关系曲线,从而获得动力能力谱曲线。其次,采用与静力谱法分析步骤2~4相同的步骤,分析结构在不同的强度水平下的位移放大系数需求值,其分析原理如图1所示。

图1 动力能力谱方法Fig.1 Dynamic capacity spectrum method
3 结构设计、有限元模型建立与试验验证
3.1 结构设计、有限元模型与地震动选取
严格按《建筑抗震设计规范》GB 50011—2010,考虑6、7、8三个设防烈度,设计了3、5、8、10、12层总共15个RC规则框架结构。平面布置均相同,底层层高为3.9 m,其余楼层层高为3.3 m。例如5层RC框架结构的平、立面如图2所示。结构荷载、混凝土强度、钢筋、梁、柱尺寸、基本周期及建模原则见参考文献[9]。
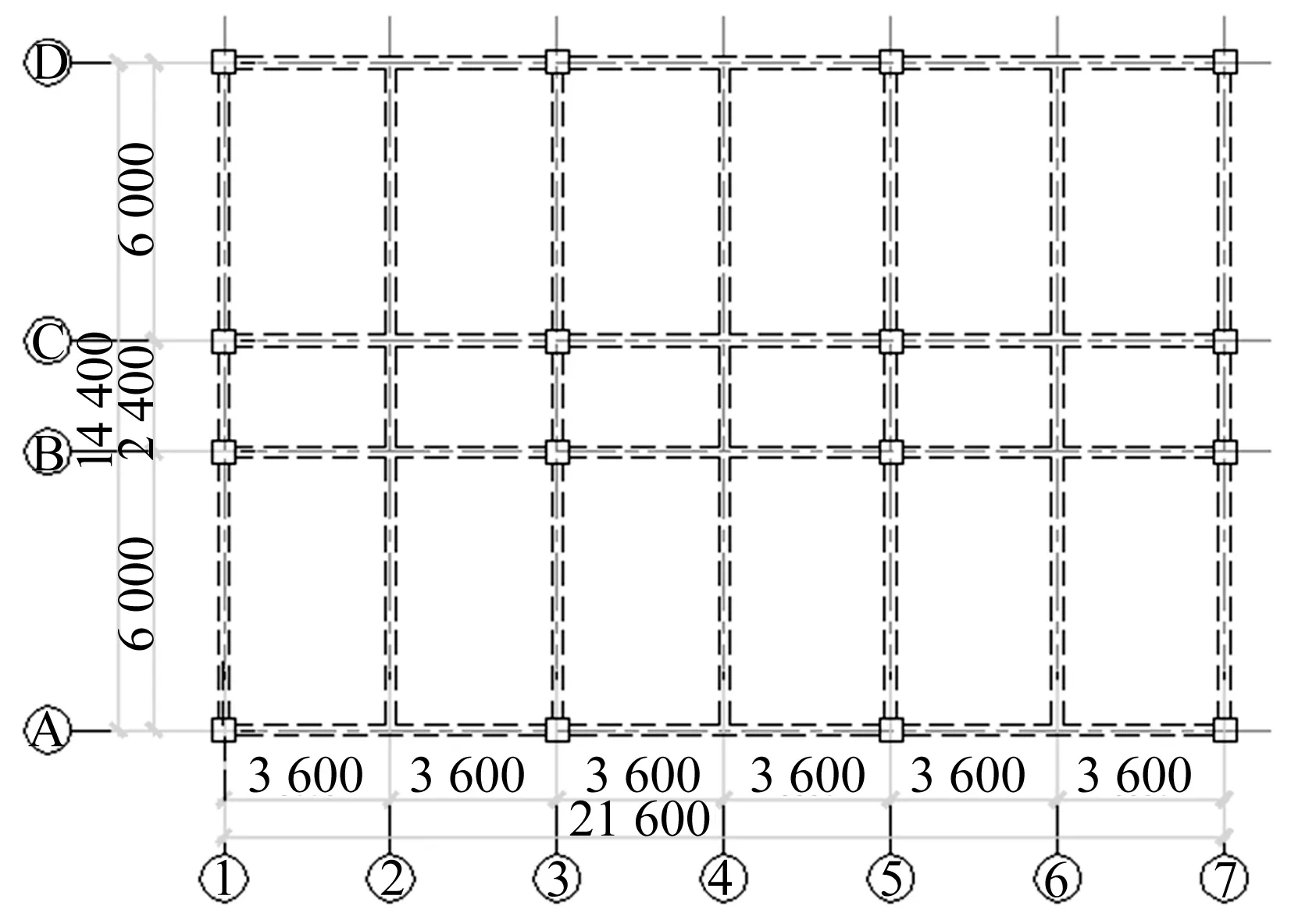
图2 结构平面布置图(m)Fig.2 Plan view of RC frame structures(m)
基于修正后的PEER强震数据库[10],根据地震事件参数和地震动参数进行了地震动记录的选择,力求在较宽的Mw-R范围内选取地震动,不考虑具有特殊性质的近断层地震动。共选择了不同强度,不同震中距的20条地震动。它们平均分布在LMSR(6.5 图3 地震动记录的反应谱Fig.3 Individual and median spectra for ground motion records 3.2 基于结构振动台试验数据的模型验证 课题组完成了一个1:2模型的2×1跨的4层RC框架结构的振动台试验。试验结构平面图和试验模型见图4,底层层高为3.6 m,其余楼层层高为3.0 m。 图4 试验结构模型Fig.4 Test model construction 基于与文中有限元模型建模一致的基本原则,建立试验结构的OpenSees有限元模型并进行分析,发现采用文中的建模原则可以较好地反映结构整体动力特性,如图5所示,其中,测点2、3、4、5分别布置在2、3、4、5层A轴交2轴的柱子上。 图5 NorthRidge地震动(PGA=0.30 g)激励下试验模型的位移响应试验值与有限元模拟值对比分析Fig.5 Comparison of test values and simulation values under the NorthRidge earthquake (PGA=0.30 g) 4.1 基于静力能力谱法的位移放大系数需求分析 采用静力能力谱法得到了15个结构在不同强度需求谱作用下的性能点。以按7度设计的8层RC框架结构为例,其分别在0.12 g需求谱和0.50 g需求谱作用下与能力谱的叠加曲线图,见图6。将图中性能点所对应的目标谱位移转换成顶点位移Δe。可知,结构在中震下未发生整体屈服,因为其目标位移仍位于弹性阶段。 根据目标位移得到的15个结构的位移放大系数需求值如图7所示。可见,中震作用下,分别按6度、7度、8度设计的结构的位移放大系数需求值分别介于0.95~2.10、0.96~2.22、1.09~2.59之间。其最小值约为1,此时结构仍位于弹性阶段,表明结构设计的保守;大震作用下,其需求值分别介于2.45~6.16、4.03~10.70、5.53~9.37之间,由最小值原则,可分别取为2.0、3.5、5.0。 图7 6、7、8度设防结构的位移放大系数需求值Fig.7 Demand values of structural displacement amplification factors 4.2 基于动力能力谱法的位移放大系数需求分析 采用选取的20条地震动,通过不断调幅将每条地震动强度逐步增大,直到结构倒塌,以阻尼比5%时结构第一自振周期所对应的谱加速度为纵坐标,以结构的最大层间位移角为横坐标,得到20条地震动作用下结构的IDA曲线,如图8所示。采用2.2节的分析方法,得到不同强度水平下结构位移放大系数需求值。以7度3层RC框架结构为例,最大谱加速度为0.90 g时,结构分别在三条地震动作用下的需求谱与能力谱叠加曲线如图9所示。图9中不同曲线表明了同一个结构在不同地震动作用下的反应不同。 采用动力能力谱法得到的结构位移放大系数需求值见图10。分别按6、7、8度设计的RC框架结构,中震作用下,其位移放大系数需求值分别介于0.51~1.91、0.49~1.93、0.56~2.24之间。大震作用下,其值分别介于1.28~4.82、1.40~4.89、1.37~5.56之间。中震作用下,按《建筑抗震设计规范》GB 50011—2010设计的结构没有达到整体屈服,规范比较保守。 注:图中每条曲线为一条地震动作用下结构的IDA曲线。图8 钢筋混凝土框架结构IDA曲线Fig.8 IDA curves of RC frames 图9 7度3层结构动力能力谱与需求谱叠加图Fig.9 Dynamic capacity spectrum method of 3-story-7-degree structure 图10 结构位移放大系数需求值Fig.10 Demand values of structural displacement amplification factors 4.3 动力能力谱法与静力能力谱法分析结果对比 采用动力能力谱法和静力能力谱法得到的结构位移放大系数需求值的比值如图11所示。可知,当结构为3层时,采用动力能力谱法和静力能力谱法得到的结构位移放大系数需求值之比接近于1,但是随着层数的增加,此比值越来越小,即两者的计算结果相差越来越大,尤其是10层以上结构,两者相差较大。这是因为动力能力谱法可以考虑结构的高阶效应,而静力能力谱法却不能。 在中震作用下,分别按6、7、8度设计的结构,采用动力能力谱法和静力能力谱法得到的结构位移放大系数需求值之比的中位值分别为0.59、0.54、0.57。在大震作用下,比值的中位值分别为0.51、0.36、0.39。 图11 采用动力能力谱法和静力能力谱法得到的结构位移放大系数之比Fig.11 Ratios of structural displacement amplification factors analyzed by dynamic capacity spectrum method with respect to those analyzed by static capacity spectrum method 文中采用提出的动力能力谱方法,对RC框架结构在不同设防水准下的位移放大系数需求值进行了分析,并将分析结果与传统静力能力谱方法分析结果进行对比分析。主要结论如下: (1)按6、7、8度设计的结构在中震作用下其位移放大系数需求值范围分别为0.51~1.91、0.49~1.93、0.56~2.24。大震作用下,分别1.28~4.82、1.40~4.89、1.37~5.56。 (2)采用文中提出的动力能力谱方法可以有效地分析结构在地震作用下的位移放大系数需求值,改善静力能力谱方法中动力需求谱与静力能力谱曲线的不和谐性。 (3)中震作用下,按《建筑抗震设计规范》GB 50011—2010设计的结构没有达到整体屈服,规范比较保守。 [1] FARAHI M, MOFID M. On the quantification of seismic performance factors of chevron knee bracings, in steel structures [J]. Engineering Structures, 2013, 46: 155-164. [2] SAMIMIFAR M, OSKOUEI A V, ROFOOEI F R. Deflection amplification factor for estimating seismic lateral deformations of RC frames[J]. Earthquake Engineering and Engineering Vibration, 2015, 14(2): 373-384. [3] AHMAD Z, SHAHZADA K, GENCTURK B, et al. Seismic capacity assessment of unreinforced concrete block masonry buildings in pakistan before and after retrofitting[J]. Journal of Earthquake Engineering, 2015, 19(3): 357-382. [4] KUYLMAZ A, TOPKAYA C. Displacement amplification factors for steel eccentrically braced frames[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(2):167-184. [5] WISNUMURTI, DEWI S M, SOEHARDJONO A. Strength reduction factor ( R ) and displacement amplification factor (Cd) of confined masonry wall with local brick in Indonesia [J]. Procedia Engineering, 2014,95: 172-177. [6] 童根树, 苏健. 联肢剪力墙的刚度、稳定性以及二阶效应[J]. 工程力学, 2012, 29(11): 115-122. TONG Genshu, SU Jian. Rigidity & buckling of coupled shear walls and second order effect [J]. Engineering Mechanics, 2012, 29(11): 115-122. [7] 童根树, 蔡志恒, 张磊. 双周期标准化的位移放大系数谱[J]. 重庆大学学报(自然科学版), 2011, 34(10), 68-75. TONG Genshu, CAI Zhiheng, ZHANG Lei. Normalized inelastic deformation ratio spectra[J]. Journal of Chongqing University (Natural Science Edition),2011,34(10) , 68-75. [8] 金双双, 郭兰慧, 戎芹, 等. 方钢管混凝土框架-钢板剪力墙结构抗震分析[J]. 应用基础与工程科学学报, 2013, 21(6):1145-1156. JIN Shuangshuang, GUO Lanhui, RONG Qin, et al. Analysis of concrete filled square steel tubular frame-steel plate shear wall structural systems [J]. Journal of Basic Science and Engineering, 2013, 21(6):1145-1156. [9] 李宇, 王森, 车艳阳, 等. 梁式桥抗震设计的弹塑性位移反应谱[J]. 振动与冲击, 2015, 34(10): 1-5. LI Yu, WANG Sen, CHE Yanyang, et al. Elasto-plastic response spectra for beam bridge’s aseismic design [J]. Journal of Vibration and Shock,2015, 34(10): 1-5. [10] 陈伟宏, 崔双双, 吕大刚, 等.钢筋混凝土框架结构位移放大系数能力分析[J]. 土木工程学报, 2014, 47(8): 47-55. CHEN Weihong, CUI Shuangshuang, LÜ Dagang, et al. Capacity analysis for structural displacement amplification factor of reinforced concrete frames[J]. China Civil Engineering Journal,2014,47(8): 47-55. [11] 吕大刚, 崔双双, 陈志恒. 基于Pushover分析的钢筋混凝土框架结构抗侧向倒塌能力评定[J]. 工程力学, 2013, 30(1), 180-189. LÜ Dagang, CUI Shuangshuang, CHEN Zhiheng. Assessment of sidesway collapse resistant capacity of reinforced concrete frame structures based on pushover analysis [J].Engineering Mechanics, 2013, 30(1), 180-189. Structural displacement amplification factor of RC frames based on the dynamic capacity spectrum method CHEN Weihong1,2, JIANG Ren1, GUI Shuangshuang3, WU Bo3 (1. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China; 2. College of Civil Engineering, Southeast University, Nanjing 210096, China; 3.College of Civil Engineering, Fujian University of Technology, Fuzhou 350108, China) Structural displacement amplification factor (DAF) is the key factor in seismic design, which is used to predict maximum inelastic deformations of structures under earthquake excitation. However, DAF has not been introduced in the current Chinese seismic design code. In this paper, 15 RC frame buildings which were 3-, 5-, 8-, 10-, 12-story buildings in different seismic fortification intensity Ⅵ, Ⅶ, Ⅷ were designed according to the Code for Seismic Design of Buildings GB 50011—2010. The FE models of these buildings were modeled and structural seismic response was analyzed. Shaking table test of a RC frame structure has been accomplished and the FE models were verified and validated. The “demand” values of the structural DAF of these RC frames were evaluated by the dynamic capacity spectrum method, and the analysis results were compared with that analyzed by the traditional static capacity spectrum method. For the designed RC frames in the seismic fortification intensity VI, VII, VIII zones, the ranges of demand values of structural DAF are 0.51-1.91, 0.49-1.93, and 0.56-2.24 respectively when they are under fortification earthquakes.The ranges of demand values of structural DAF are 1.18-4.05, 1.33-3.45, and 1.42-2.66 respectively when they are under rare earthquakes.The overall yield of the codified designed RC frames under fortification earthquakes has not occurred. And it is shown that the Chinese seismic design code is conservative. dynamic capacity spectrum method; static capacity spectrum method; structural displacement amplification factors; demand values; RC frame structures 国家自然科学基金(51408131;51478118;51508099);福建省科技厅引导性项目(2016Y0061);福建省教育厅科技项目(JA15351) 2015-10-23 修改稿收到日期:2015-12-04 陈伟宏 男,博士后,副研究员,1980年生 吴波 男,福建省闽江学者(特聘教授),1971年生 E-mail: cshuangshuang@163.com P315.9 A 10.13465/j.cnki.jvs.2016.24.007


4 RC框架结构位移放大系数的需求分析


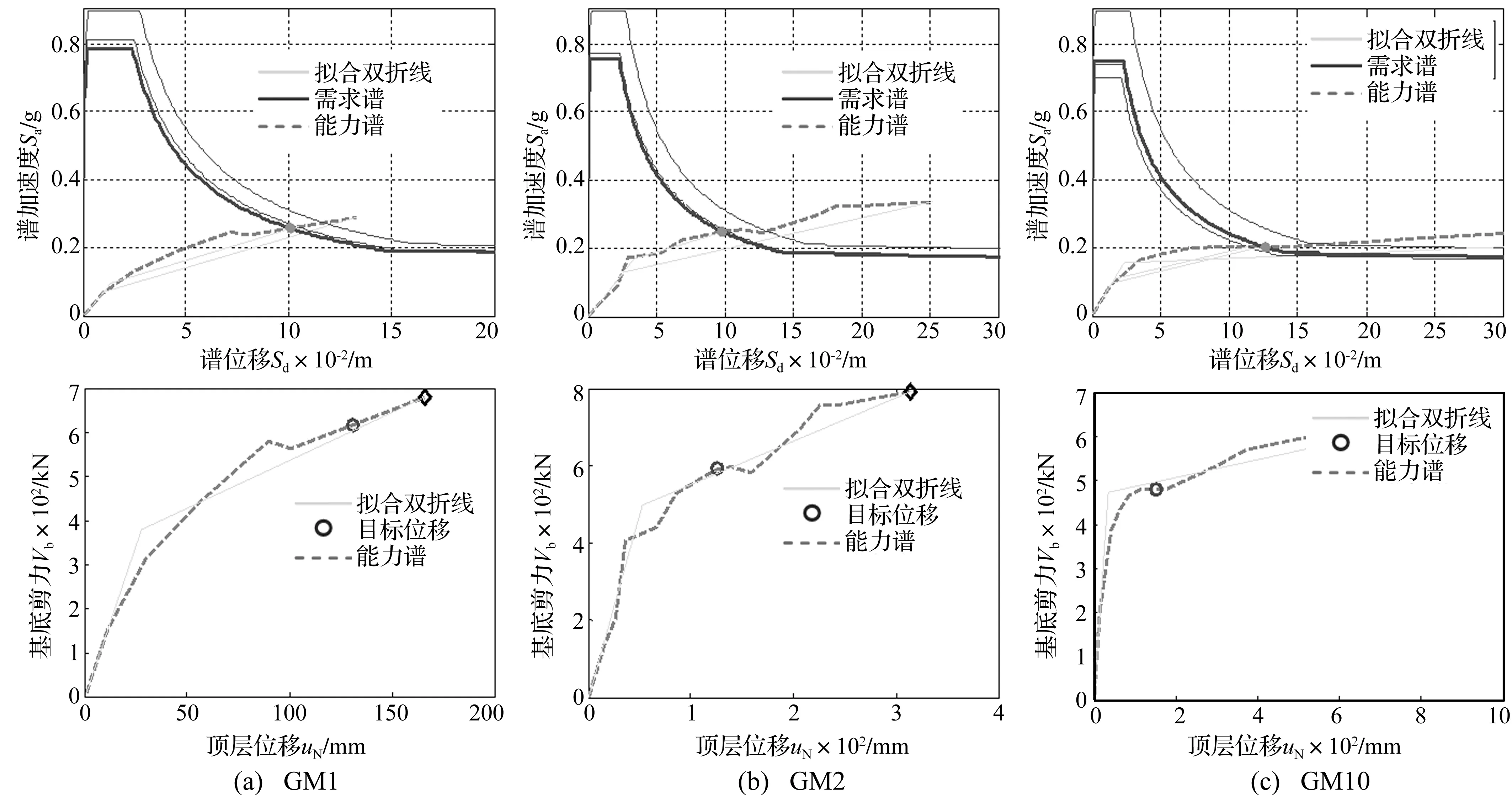

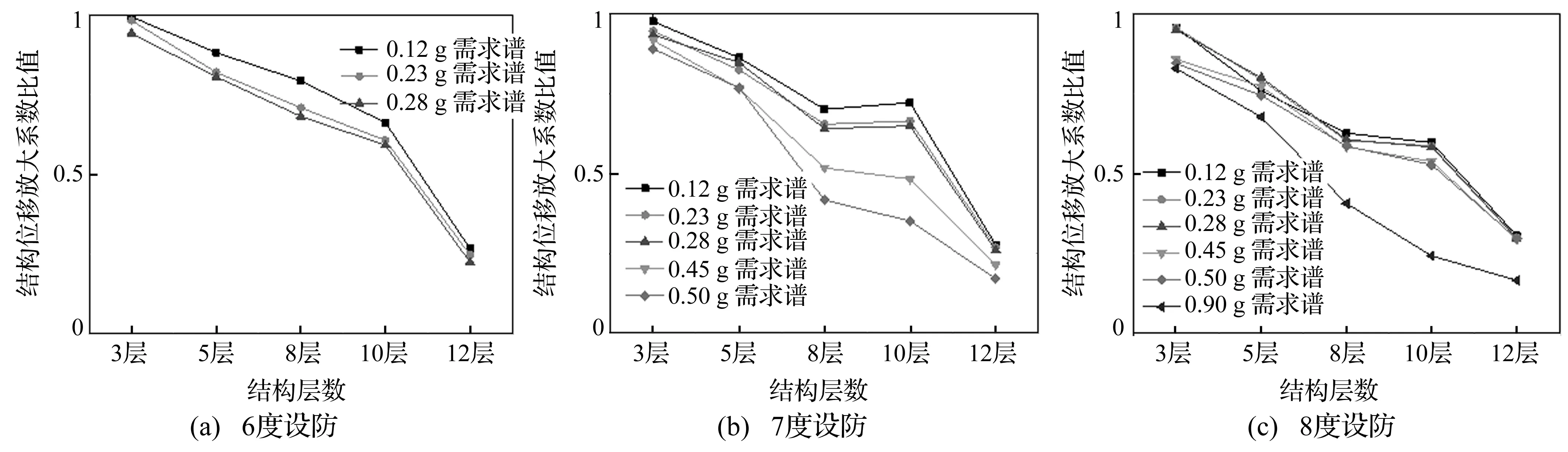
5 结 论
