CALIOP数据在星载相干多普勒测风激光雷达性能仿真中的应用❋

卢 博， 吴 东， 张天澈

(中国海洋大学信息科学与工程学院，山东 青岛 266100)

CALIOP数据在星载相干多普勒测风激光雷达性能仿真中的应用❋

卢 博， 吴 东❋❋， 张天澈

(中国海洋大学信息科学与工程学院，山东 青岛 266100)

利用2007—2008年21个月CALIOP测量的夜间气溶胶后向散射系数的全球三维平均分布数据取代传统仿真中的气溶胶模型数据，对晴空条件下的2.1 μm相干多普勒测风激光雷达的测风性能进行了计算机仿真研究。仿真结果表明，采用合理的系统参数设计，在20°S至40°N之间4.5 km海拔之下单激光脉冲的径向风速误差普遍小于1 m/s。以1 m/s作为可接受风速误差的标准，符合标准的最大可测量海拔高度向两极方向递减，在南极附近减至1～2 km。若10个激光脉冲平均测量，在对流层下层风速误差可降至0.5 m/s以内，且在35°N附近最大可测量海拔高度可达5.5 km。

CALIOP；相干多普勒测风激光雷达；性能仿真；气溶胶后向散射系数

全球大气风场的精确测量对数值气象预报、气候变化研究、飓风预报、机场风切变的探测等都有重大意义。早在1984年，Huffaker提议使用星载多普勒二氧化碳激光雷达进行全球风测量[1]。随着激光技术的发展，2 μm高能量固体激光器成功研发，它相比二氧化碳激光器能够提供更多的参数，并且被NASA应用到星载相干多普勒雷达上[2]。

星载多普勒测风激光雷达是目前测量全球三维风场最先进的技术，能够提供高精度、高分辨率、高全球覆盖率的大气风场信息。多普勒测风激光雷达系统发射的激光与大气中的气溶胶相互作用，产生后向散射信号，通过分析该回波信号获取风速信息。多普勒测风激光雷达可分为直接探测和相干探测2种探测方式。直接探测利用光学鉴频器直接分析大气气溶胶后向散射信号获取风场引起的多普勒频移，相干探测对接收到的气溶胶后向散射信号和稳定的本地振荡光进行混频获取风场引起的多普勒频移。与直接探测相比，相干探测方式具有信噪比高、探测灵敏度高以及对背景太阳光不敏感等优点[3]。

在卫星发射前，对星载相干多普勒测风激光雷达进行性能仿真是十分必要的。多普勒激光雷达仿真模型DLSM(Doppler Lidar Simulation Model)采用了模型化的气溶胶后向散射系数剖面实现多普勒测风激光雷达仿真[4-5]。Frehlich等使用定常和变化的气溶胶散射模型对相干多普勒测风雷达进行了大量的研究[6-9]。近年，在仿真方法上，Frehlich等采用了其提出的经验模型[8-9]。上述研究尽管考虑了风切变、气溶胶变化等因素对探测信号的影响，但是无法对全球大气气溶胶分布变化较大的实际情况给出较理想的性能仿真。

2006年4月CALIPSO(Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation)卫星成功发射，其搭载的星载激光雷达CALIOP(Cloud-Aerosol Lidar with Orthogonal Polarization)自开机测量以来，至今正常运行，对气溶胶和云的全球分布进行了前所未有的高分辨率三维观测[10]，使得考虑实际大气变化的相干多普勒测风激光雷达性能仿真成为可能。2013年，吴东等采用了Frehlich等的仿真经验模型，利用2007年3月—2008年2月1 a的CALIOP晴空条件实测资料，给出2.1 μm星载相干多普勒测风激光雷达随纬度分布的性能仿真结果[11]。本文采用菲涅耳(Fresnel)近似条件下的参数物理意义明晰的路径积分仿真方法[12]，利用更长时间的CALIOP晴空条件实测资料，将CALIOP 2007—2008年21个月(剔除了2008年8、9、10月)的气溶胶后向散射数据应用于晴空条件下2.1 μm星载相干多普勒测风激光雷达的测风性能仿真之中，给出随纬度分布和随经度分布的性能仿真结果。

1 相干多普勒测风激光雷达原理

对于相干多普勒测风激光雷达系统性能的评估可用径向风速的均方根误差表示，1984年Kane[13]给出由信噪比SNR估算均方根误差的公式：

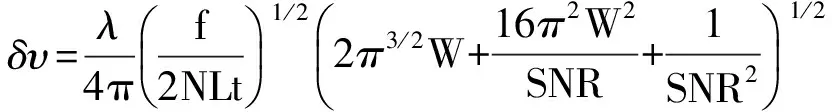
(1)

其中：f是采样频率；N是激光脉冲数；t是脉冲发射间隔；L是距离门宽度和脉冲宽度的比值；λ是波长；W是无噪声返回信号的频率展延，其计算公式为：

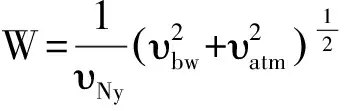
(2)

其中：υNy=fλ/2是由奈奎斯特判据得到的最大速度；υbw=λ/(4πt)是对应发射脉冲宽带的速度不确定性；υatm为风速分布的标准偏差。因此，为了减小误差，由等式(1)可以看出需减小W的值，即减小υbw的值，增大脉冲间隔t。当脉冲间隔t极大时υbw极小，此时W的大小由υatm决定。需要注意的是，由于分子快速随机的运动，分子散射会出现明显的多普勒展宽，最终导致υatm值的变大。因此，为避免分子散射的影响，应选择更长的激光波段，使得相干激光雷达性能的评估依赖于气溶胶的后向散射系数。

当信噪比SNR极大时，等式(1)中的最后2项极小，速度测量的误差达到极小。信噪比是另一个减小风速测量误差的关键参数，1991年Frehlich和Kavaya[12]提出SNR的计算方法为：

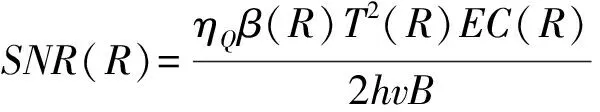
(3)

其中：E是激光脉冲能量；R是雷达到脉冲前沿的距离；T(R)是激光雷达到距离R处的大气单程透过率；B是探测带宽；h是普朗克常数；υ是激光频率；ηQ是量子效率，C(R)是无量纲的相干响应率。外差效率ηH是评估相干多普勒测风雷达的重要参量，定义为ηH=C(R)/D(R),其中D(R)是无量纲的非相干响应率。C(R)和D(R)都可由低频空间(lf)分量和高频空间分量(hf)两部分表示[12]，可用它们的一阶近似项代替，表达式如下：

(4)

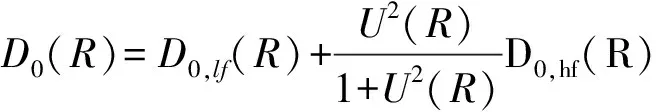
(5)

其中：

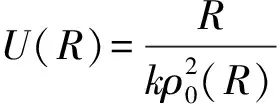
(6)

(7)

是横向相干长度；波矢k=2π/λ(rad/m)，常数H=2.914 383,Cn2是折射率扰动结构参数,C0,lf(R)、C0,hf(R)、D0,lf(R)、D0,hf(R)具体算法Frehlich和Kavaya已给出。当目标的波动强度较小时，低频分量起主导作用，对于任何强度的波动低频分量是不可缺少的部分。当目标的波动强度较大时,高频分量开始变得重要。对于星载激光雷达观测，由于卫星在几百公里高的轨道上，目标大气远离雷达，晴空条件下，目标大气的折射率扰动对外差探测的影响较小。

2.1 μm波长的大气气溶胶后向散射系数可由CALIOP提供的532 nm的气溶胶后向散射系数转换得到。Srivastava等人[14]通过对波长范围在0.53～10.6 μm的多套激光雷达的实测资料分析给出了2.1 μm大气气溶胶后向散射系数波长转换公式：

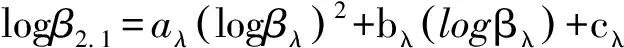
(8)

其中，当波长λ为532 nm时，具体参数为a532=0.023 05，b532=1.709，c532=2.793[14]。本文所选用的CALIOP数据为2007和2008年21个月Level 2 V3.01气溶胶剖面数据提供的晴空条件下夜间的气溶胶后向散射系数。数据水平分辨率5 km，垂直分辨率60 m，高度范围0～30 km。

2 性能仿真及结果分析

本文基于MATLAB编程语言，开发了一套系统参数可调的相干激光雷达仿真软件，对星载相干多普勒测风激光雷达性能进行仿真。使用的系统参数如表1所示。对相干多普勒测风激光雷达进行性能仿真时，首先使用晴空条件下测得的折射率扰动结构参数Cn2计算外差效率[15]。在激光下行传输时Cn2会对外差效率ηH产生累积影响，导致越接近地表时外差效率率ηH越小。大气折射率对外差效率的影响是很小的，并且主要是由雷达系统引起的[11]。本文使用了冬季夜间的Cn2数据计算外差效率。

为了实现更加真实的性能仿真，本文只选用了晴空条件下的后向散射系数数据。选取数据时，使用的条件是消光系数质量分类标识等于1、2、16或18，消光系数不确定性小于3 km-1，层分辨率为5或20 km，同时滤掉检测到为80 km分辨率的气溶胶层。出现晴空条件的分布模式是由全球的云分布模式确定的，此模式对相干多普勒雷达的性能仿真具有十分重要的影响[11,16]。

表1 星载相干多普勒测风激光雷达系统参数

图1为2007和2008年2 a 24个月全球4°×6°分辨率532 nm的夜间平均气溶胶后向散射系数分布图，自下到上分别是1、3和5 km的高度分布图，色标代表后向散射系数值取以10为底的对数，单位为km-1。从全球范围来看，大部分气溶胶分布在高度小于1 km的边界层内。由图1可以看出，在南纬20°至北纬40°区域内，后向散射数值普遍偏大，这是由于在北非、中东、东亚地区存在大面积沙漠，在中非、南非、南美地区存在生物燃烧行为，非洲大量的烟尘随着大气运动被运输到大西洋上空导致的。同时可以看出，气溶胶后向散射系数由赤道地区向南北两级方向递减，在两级地区趋近于0。

图1 全球4°×6°分辨率532 nm的夜间平均气溶胶后向散射系数(10为底的对数)分布图，自下到上分别是1、3、5 km的高度分布图。白色区域对应地点的海拔高于高度选择，因此没有可用的数据

为了便于观察后向散射系数随高度的变化，将24个月全球4°×6°分辨率532 nm的夜间平均后向散射系数分别在经度和纬度方向上进一步的平均。图2为24个月532 nm夜间平均后向散射系数随纬度的垂直分布，异常的数据分布在50°N到80°N纬度上7～10 km高度范围内(图2右上红圈部分)。这很可能与2008年8月7日的Kasatochi火山爆发[17]有关(http://alaska.usgs.gov/science/kasatochi/)。阿拉斯加火山观测站报导称2008年8月8日之后有持续的火山灰进入大气中，且火山灰在9.1～13.7 km海拔范围内纬度方向上自东向西漂移了950 km以上(http://www.volcano.si.edu/volcano.cfm?vn=311130)。因此，本文去掉2008年8、9、10三个月的CALIOP后向散射系数数据，只将剩余的21个月的数据应用到相干多普勒雷达性能仿真中。图3(a)为21个月532 nm夜间平均后向散射系数随纬度的垂直分布，异常部分已经消失，图3(b)为使用公式(8)后得到的21个月2.1 μm夜间平均后向散射系数随纬度的垂直分布。由图3可以看出，在20°S到40°N纬度范围内5 km高度以下存在较大的后向散射系数数值。图4为21个月532 nm和2.1 μm夜间平均后向散射系数随经度的垂直分布。

图2 24个月532 nm夜间平均后向散射系数随纬度的垂直分布

((a)21个月532 nm的夜间平均后向散射系数随纬度的垂直分布Zonal-vertical distributions of mean backscatter at 532 nm derived from 21 months of nighttime data;(b)21个月2.1 μm的夜间平均后向散射系数随纬度的垂直分布Zonal-vertical distributions of mean backscatter at 2.1 μm derived from 21 months of nighttime data.)

图3 21个月532 nm和2.1 μm的夜间夜间平均后向散射系数随纬度的垂直分布

Fig.3 Zonal-vertical distributions of mean backscatter at 532 nm and 2.1 μm derived from 21 months of nighttime data

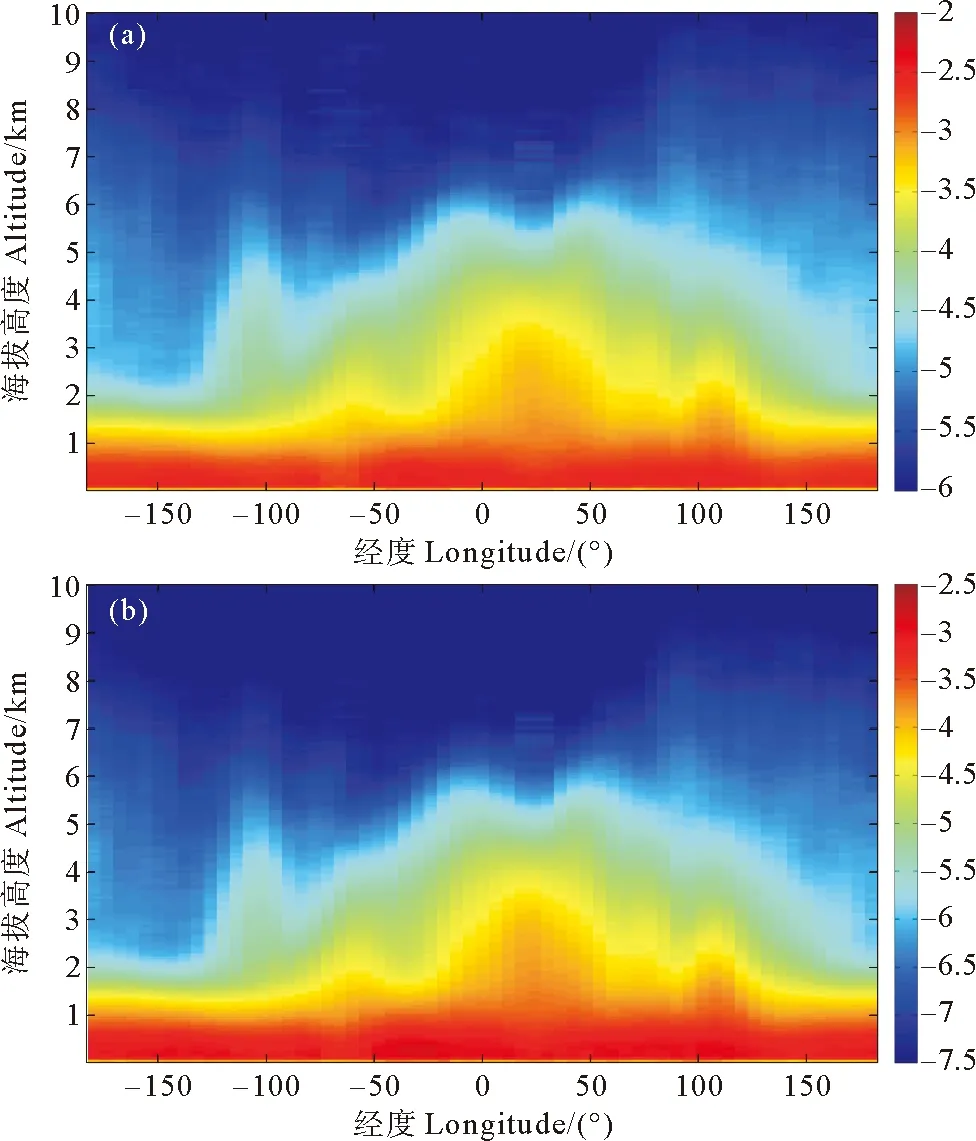
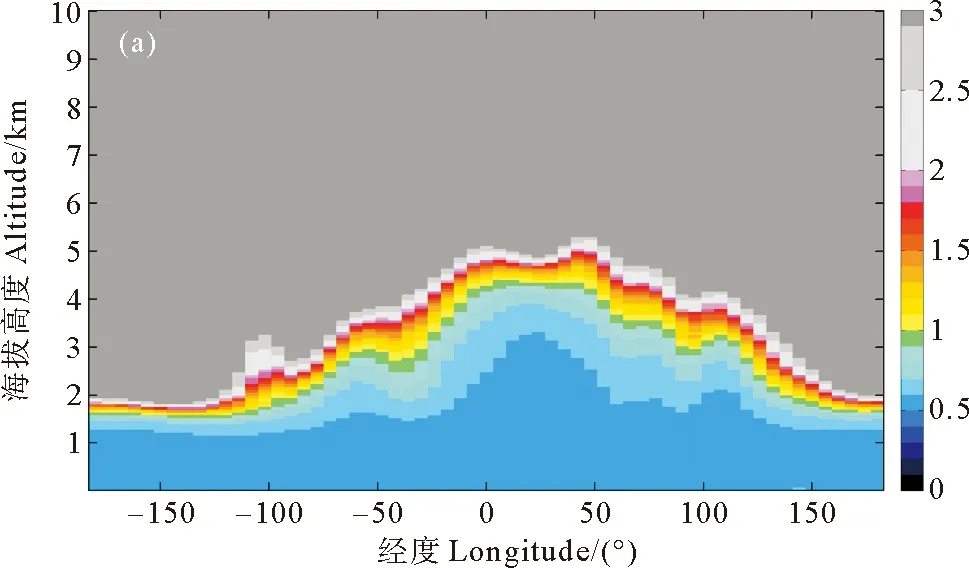
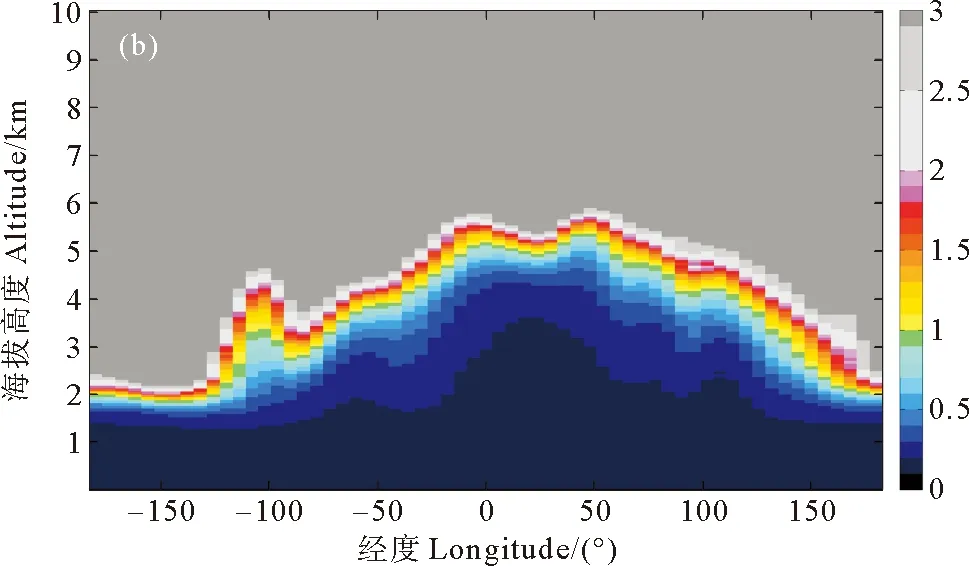
(a)21个月532 nm的夜间平均后向散射系数随经度的垂直分布。Longitudinal-vertical distributions of mean backscatter at 532 nm derived from 21 months of nighttime data ;(b)21个月2.1 μm的夜间平均后向散射系数随经度的垂直分布。Longitudinal-vertical distributions of mean backscatter at 2.1 μm derived from 21 months of nighttime data.

图4 21个月532 nm和2.1 μm的夜间夜间平均后向散射系数随经度的垂直分布

Fig.4 Zonal-vertical distributions of mean backscatter at 532 nm and 2.1 μm derived from 21 months of nighttime data

根据2.1 μm气溶胶后向散射系数的垂直分布和扰动结构参数Cn2，用公式(1)计算风速测量的误差，在计算时激光脉冲数N分别取1和10进行对比。图5为径向速度误差随纬度垂直分布的仿真结果，图6是径向速度误差随经度垂直分布的仿真结果。

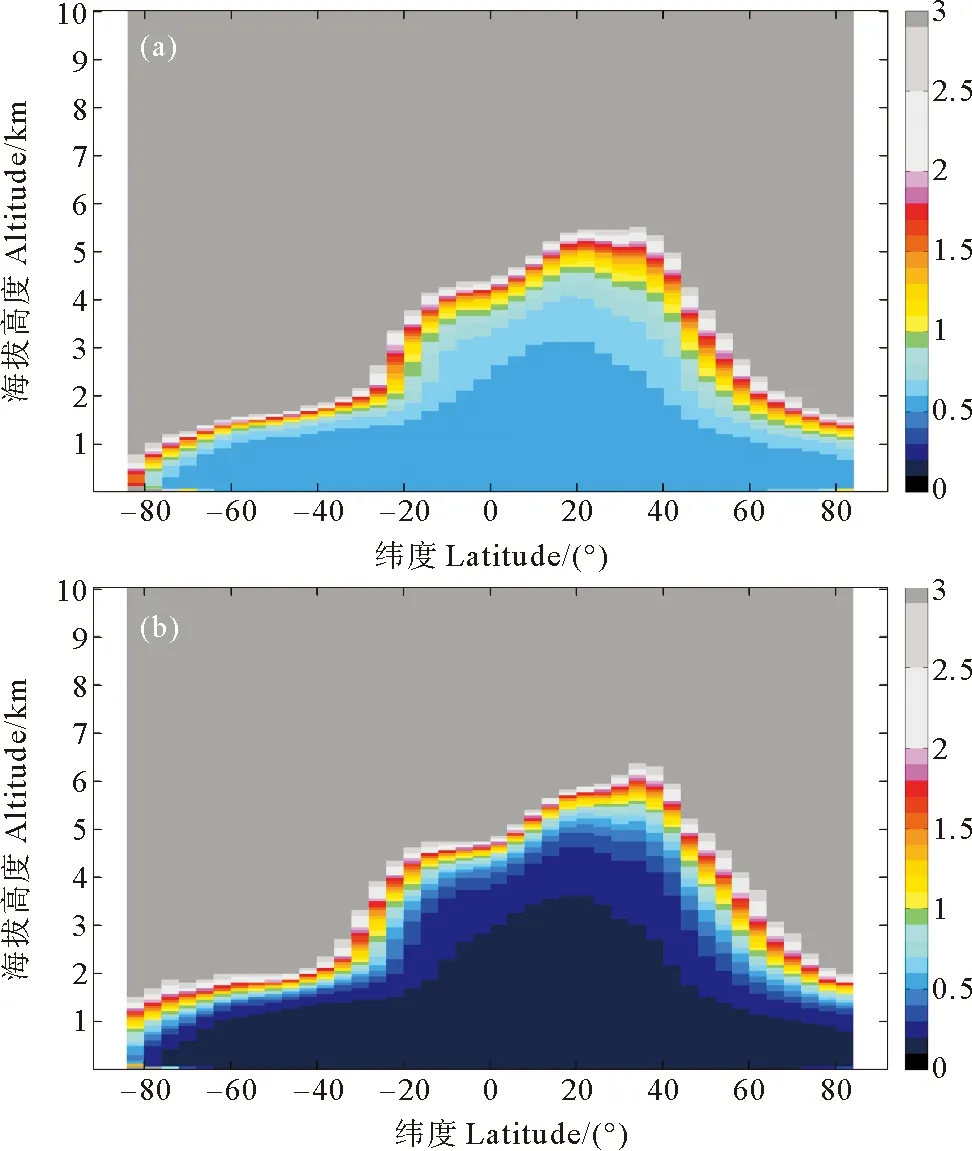
((a)N=1计算得到的误差分布图Single pulse(N=1);(b)N=10计算得到的误差分布图Ten pulses (N=10).)

图5 速度误差随纬度的垂直分布(色标单位为m/s)

Fig.5 Zonal-vertical distributions of speed error (Colors are coded in m/s)

((a)N=1计算得到的误差分布图Single pulse(N=1);(b)N=10计算得到的误差分布图ten pulses(N=10))

图6 速度误差随经度的垂直分布(色标单位为m/s)

Fig.6 Longitudinal-vertical distributions of speed error(Colors are coded in m/s)

相干多普勒测风激光雷达是通过测量气溶胶粒子运动的多普勒频移实现风速测量。由于较强的气溶胶后向散射信号普遍来源于对流层下层，在低海拔地区计算的风速精度更高。如图5所示，径向风速测量精度最高的部分均是在对流层下层。单激光脉冲(N=1)测量时，仿真得到的径向风速误差大于0.5 m/s小于1 m/s区域的海拔在低纬度地区普遍小于4.5 km，在高纬度地区普遍小于1.5 km。同时从图5可以发现，对比相同误差值发生的高度，北半球略高于南半球，这种非对称分布的原因是由于南北半球气溶胶分布不同引起的。北半球干旱和半干旱地区面积、人口数量均大于南半球，因此北半球大气中存在更多的沙尘性气溶胶和人为源气溶胶。

如果以1 m/s作为可接受风速误差的标准，则符合标准的最大可测量海拔高度出现在20°N，此高度值约5 km，在20°N附近，非洲的沙尘在沙尘源地区可传输至7 km的海拔高度上[18]。当激光脉冲数N取10时，在对流层下层风速误差可以减0.5 m/s范围以内。此时符合标准的最大可测量海拔高度出现在35°N，高度值约5.5 km，而在35°N附近，亚洲的沙尘可传输到上对流层[19]。因此可以得到结论，合理设计的相干多普勒测风激光雷达可用于获得晴空条件对流层下层的风廓线。

在图6中，速度误差随经度的垂直分布大体上以20°E线为轴左右对称，在20°W至50°E范围内径向风速测量精度最高。这是由于在此经度范围内，存在大量的生物质燃烧现象，产生大量的烟尘扩散到2 km以上的高空造成的[20]。在以1 m/s作为可接受风速误差的标准，所有经度范围内符合标准的最大可测量海拔高度在N=1时最大值为4.5 km，在N=10时最大值为5 km，且最大可测量海拔高度普遍大于2 km。实际气溶胶后向散射系数的分布与地表类型等有关系，在90°W至120°W经度区间内，存在众多高原和山脉，如墨西哥高原、落基山脉等等，导致100°W处小峰的出现。

3 结论

本文采用MATLAB编程，选用了2007—2008年2 a的CALIOP V3.01二级(Level 2)夜间气溶胶剖面数据，剔除了2008年8、9、10月异常气溶胶数据，获得气溶胶后向散射系数的全球三维平均分布数据。对晴空条件下的2.1 μm星载相干多普勒激光雷达进行性能仿真。仿真结果表明，采用合适的系统设计和合理的参数选择，使用相干多普勒测风激光雷达从太空对对流层底的全球风速激光测量是可行的。

采用合理的光学和数据采集参数，当单激光脉冲测量时径向风速误差在20°S至40°N之间4.5 km海拔之下小于1 m/s。以1 m/s作为可接受风速误差的标准，符合标准的最大可测量海拔高度向两极方向递减，在南极附近减至1～2 km。若平均10个激光脉冲进行仿真，在对流层下层风速误差可降至0.5 m/s以内，且在35°N附近最大可测量海拔高度可达5.5 km。

进一步的应用CALIOP多种天气条件下的实际观测的气溶胶后向散射系数取代传统仿真中的气溶胶模型数据，对于星载测风激光雷达的发射前系统设计、参数选择、性能估计等将有重要意义。

致谢:感谢美国国家航空航天局兰利研究中心的科学数据中心(ASDC)提供的CALIOP观测数据。

[1] Huffaker R M, Lawrence T R, Post M J, et al. Feasibility studies for a global wind measuring satellite system (Windsat): Analysis of simulated performance[J]. Applied Optics, 1984, 23(15): 2523-2536.

[2] Baker W E, Emmitt G D, Robertson P, et al. Lidar measured winds from space: an essential component for weather and climate prediction[J]. Bull Am Meteorol Soc, 1995, 76: 869-888;

[3] Huffaker R M, Hardesty R M. Remote sensing of atmospheric wind velocities using solid-state and CO2coherent laser systems [J]. Proceedings of the IEEE, 1996, 84(2): 181-204.

[4] Wood Jr S A, Emmitt G D, Greco S. DLSM: A coherent and direct detection lidar simulation model for simulating space-based and aircraft-based lidar winds[C]. AeroSense: International Society for Optics and Photonics, 2000: 2-12.

[5] Wood S A, Emmitt G D, Wood L S, et al. The community Doppler lidar simulation model (DLSM)[EB/OL]. http: //www. swa. com/ald/DLSM4. 2/DLSMindex. htm. [2007-07-02],[2014-01-20].

[6] Frehlich R G, Yadlowsky M J. Performance of mean-frequency estimators for Doppler radar and lidar[J]. Journal of Atmospheric and Oceanic Technology, 1994, 11(5): 1217-1230.

[7] Lottman B T, Frehlich R G. Evaluation of coherent Doppler lidar velocity estimators in non-stationary regimes[J]. Applied Optics, 1997, 36: 7906-7918.

[8] Frehlich R. Simulation of coherent Doppler lidar performance for space-based platforms[J]. Journal of Applied Meteorology, 2000, 39(2): 245-262.

[9] Frehlich R. Errors for space-based Doppler lidar wind measurements: Definition, performance, and verification[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(11): 1749-1772.

[10] Winker D M, Hunt W H, McGill M J. Initial performance assessment of CALIOP[J]. Geophysical Research Letters, 2007, 34(19).

[11] Wu D, Tang J, Liu Z, et al. Simulation of coherent Doppler wind lidar measurement from space based on CALIPSO lidar global aerosol observations[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, 122: 79-86.

[12] Frehlich R G, Kavaya M J. Coherent laser radar performance for general atmospheric refractive turbulence[J]. Applied Optics, 1991, 30(36): 5325-5352.

[13] Kane T J, Zhou B, Byer R L. Potential for coherent Doppler wind velocity lidar using neodymium lasers[J]. Applied optics, 1984, 23(15): 2477-2481.

[14] Srivastava V, Rothermel J, Clarke A D, et al. Wavelength dependence of backscatter by use of aerosol microphysics and lidar data sets: Application to 2. 1-μm wavelength for space-based and airborne lidars[J]. Applied Optics, 2001, 40(27): 4759-4769.

[15] Fairall C W, FRISCH A S. Diurnal and annual variations in mean profiles of Cn 2[M]. Boulder: NOAA Technical Memorandum ERL WPL-195 (National Oceanic and Atmospheric Administration), 1991.

[16] Wu D, Hu Y, Mccormick M P, and Yan F. Global Cloud Layer Distribution Statistics from One Year’s CALIPSO Lidar Observations[J]. International Journal of Remote Sensing, 2001, 32(05): 1269-1288.

[17] Wang J, Park S, Zeng J, et al. Modeling of 2008 Kasatochi volcanic sulfate direct radiative forcing: assimilation of OMI SO 2 plume height data and comparison with MODIS and CALIOP observations[J]. Atmospheric Chemistry and Physics Discussions, 2012, 12(10): 26435-26475.

[18] Liu Z, Omar A, Vaughan M, et al. CALIPSO lidar observations of the optical properties of Saharan dust: A case study of long-range transport[J]. Journal of Geophysical Research: Atmospheres (1984-2012), 2008, 113(D7): 102-108.

[19] Uno I, Eguchi K, Yumimoto K, et al. Asian dust transported one full circuit around the globe[J]. Nature Geoscience, 2009, 2(8): 557-560.

[20] Winker D M, Tackett J L, Getzewich B J, et al. The global 3-D distribution of tropospheric aerosols as characterized by CALIOP[J]. Atmospheric Chemistry and Physics, 2013, 13(6): 3345-3361.

责任编辑 陈呈超

Performance Simulation of Spaceborne Coherent Doppler Wind Lidar Based on CALIOP Data

LU Bo, WU Dong, ZHANG Tian-Che

(College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China)

A spaceborne Doppler lidar can be used to obtain the 3-dimensional (3D) global wind data. The measurement accuracy of radial wind speed depends strongly on backscattered signals from aerosols. The Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) mission, launched by NASA in April 2006, created continuous vertically resolved observations of aerosols on a near-global scale using its onboard lidar(CALIOP). Instead of using traditional modeled aerosol backscatter profiles, the measurement performances of a spaceborne 2.1 μm coherent Doppler wind lidar (CDWL) are simulated using mean zonal-vertical and longitudinal-vertical aerosol backscatter distributions retrieved from 21 months data (from Jan. 2007 to Dec. 2008 except Aug. to Oct. in 2008) of CALIOP night time measurements in clear-air conditions. The aerosol backscatters at 2.1 μm are derived from the CALIOP measurements of aerosol backscatter coefficient at 532 nm by using Srivastava’s relationship. A computer simulation tool for the measurement performance simulation of a CDWL system has been developed using MATLAB. With a laser pulse energy of 1 J and a telescope of 1 m in diameter and appropriate selected parameters, the simulated radial speed error is less than 1 m/s for a single-shot measurement within 4.5 km altitude between 20°S and 40°N. With 1 m/s as a benchmark of the acceptable speed error, the highest measurable altitude decreases toward the two poles from the equator and decreases to an level between 1 km-2 km in the southern remote ocean. The error can be further reduced to a certain value less than 0.5 m/s in the low troposphere when 10 laser shots are averaged and at the same time the measurable altitude reaches a maximum close to 5.5 km around 35°N.

CALIOP; coherent Doppler wind lidar; performance simulation; aerosol backscatter

国家自然科学基金项目(41228008；41376180)资助 Supported by the National Natural Science Foundation of China(41228008,41376180)

2014-11-15；

2015-06-20

卢 博(1989-)，男，硕士生。E-mail:lubo89@126.com

❋❋ 通讯作者：E-mail:dongwu@ouc.edu.cn

TN958.98

A

1672-5174(2017)01-119-07

10.16441/j.cnki.hdxb.20140257

卢博， 吴东， 张天澈. CALIOP数据在星载相干多普勒测风激光雷达性能仿真中的应用[J]. 中国海洋大学学报(自然科学版), 2017, 47(1): 119-125.

LU Bo, WU Dong, ZHANG Tian-Che. Performance simulation of spaceborne coherent doppler wind lidar based on CALIOP data[J]. Periodical of Ocean University of China, 2017, 47(1): 119-125.