基于流-固耦合的不同外形抗拖网海床基外部流场分析❋

于凯本， 刘保华， 杨 涛， 高 健， 李正光

(1.中国海洋大学，山东 青岛 266100； 2.国家深海基地管理中心，山东 青岛 266061； 3.青岛科技大学，山东 青岛 266061)

基于流-固耦合的不同外形抗拖网海床基外部流场分析❋

于凯本1,2， 刘保华2， 杨 涛3， 高 健3， 李正光2

(1.中国海洋大学，山东 青岛 266100； 2.国家深海基地管理中心，山东 青岛 266061； 3.青岛科技大学，山东 青岛 266061)

本文采用计算流体动力学方法(CFD)，在考虑耦合场的条件下对2种不同形状的抗拖网海床基外部流场进行了流固耦合分析。根据抗拖网海床基的外形结构，建立了抗拖网海床基流体动力学分析模型，利用ICEM CFD对其进行前处理，并利用动网格技术对模拟区域的边界条件进行了设置。根据流固2种不同耦合方式的介绍及模拟对比分析，选择了单向流固耦合方式。对两种抗拖网海床基的外部速度场以及压力进行分析研究，抗拖网海床基外部流场的数值模拟可以为进一步开展抗拖网海床基结构优化设计提供参考。

CFD； 流固耦合； 海床基； 流场； 数值模拟

抗拖网海床基主要应用于200 m水深浅海区域。根据实际应用需求，可搭载各种仪器探测海底附近的海洋参数或海洋的剖面参数，同时根据有无水面与岸基能源支持的情况，分为自容式与有缆供电式[1]。

一套典型的抗拖网海床基是由抗拖网外罩和坐底平台紧固配合，构成主舱，能够为内部搭载的仪器提供有效的保护。主舱内分成多个舱室，主要有浮体舱和回收绳索舱，浮体舱内安装有声学释放单元、回收浮体和监测仪器。同时还须辅助配有布放挂钩及声学水面甲板单元。

抗拖网海床基的外形主要以圆形和多边形为主，部分海床基为四边形，多具有流线型的外观。意大利PROTECO SUB公司的抗拖网海床基外观以圆型为主，美国Flo Tec公司则以多边形结构为特点[2-3]。圆台形的抗拖网海床基由于内部空间大，能够搭载更多的仪器设备；多边形的抗拖网海床基受内部空间的限制，仅能搭载有限的仪器，但利于布放回收。两种外形的抗拖网海床基须根据实际应用情况进行合理选择。

由于抗拖网海床基布放到海底后，会破坏布放区域原先的平衡状况，首先该区域内海流流速因抗拖网海床基的突然加入而发生改变，进而会导致海底沉积物的淤积平衡被打破，会出现抗拖网海床基底部泥沙被底流掏空导致海床基倾覆，甚至被泥沙掩埋，使得抗拖网海床基所搭载的仪器设备不能正常的工作。因此，本文根据中国近海环境情况，采用CFD软件结合流固耦合分析对两种不同外形的抗拖网海床基周围外部流场进行了数值模拟分析。分析了在单向海流作用下，两种不同外形抗拖网海床基的外部流场特点及海床基所受流场压力的影响。

1 水力学模型

直接数值模拟(DNS模型)、大涡流模拟(LES模型)、Reynolds平均方法(RANS模型)等形式的湍流模型均可以对抗拖网海床基周围流场进行模拟[4]。直接数值模拟(DNS)可以获得湍流场的精确信息，是研究湍流机理的有效手段，但是现有的计算机资源往往难以满足对高雷诺数流动模拟的需要，且其要求计算机内存容量与机时非常大。大涡模拟(LES)基于湍动能传输机制，直接计算大尺度涡的运动，小尺度涡运动对大尺度涡运动的影响则通过建立模型体现出来，但是其运行需要庞大的计算及存储能力，对大量数据处理和非线性偏微分方程的求解需要高速数值处理能力。Reynolds平均方法(RANS)对计算机的要求较低，可以很容易的从RANS方程解出湍流的统计量，几乎能对多有的雷诺数范围的工程问题进行求解[4]。

所以综合上述介绍，本文采用以雷诺时均N-S方程为基础的RNGk-ε湍流模型来模拟布放到海底之后的抗拖网海床基外部流场。这里把抗拖网海床基周围海水理想化，底流流动情况视为不可压流动。此时雷诺时均N-S控制方程可以表示为：

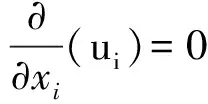
(1)

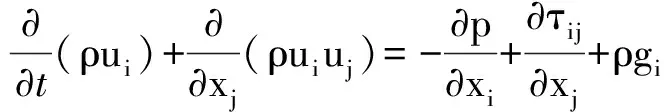
(2)

其中：xi为i方向坐标；t是时间；ρ和u代表流体的密度和速度；gi为重力加速度。

其中雷诺平均应力定义为：

(3)

RNGk-ε湍流模型中的k方程和ε方程分别表示为：

(4)

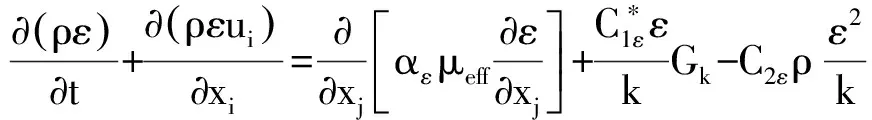
(5)

其中：

μeff=μ+μt；

Cμ=0.084 5, αk=αε=1.39；

C1ε=1.42, C2ε=1.68；

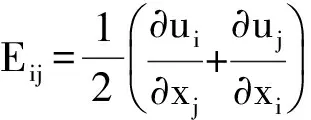
η0=4.377, β=0.012。

RNGk-ε湍流模型是针对充分发展的湍流才有效的，即高Re数的湍流模型[5]。海床基布放到海底之后，海床面及海床基表面的海流流动为近壁区内的流动，其Re数较低，这里采用壁面函数法进行模拟。

2 两种不同外形抗拖网海床基的建模

2.1 模型建立及网格划分

本文利用SolidWorks建立四棱台形和圆台形抗拖网海床基的简化模型。在流体模型的构建中去除了吊装结构，并对外罩上的开孔进行了补全，使模型外表面完整光滑。抗拖网海床基的外形如图1和2所示，其中四棱台形底边尺寸为1 800mm×1 800mm，上边尺寸为750mm×750mm，高为500mm；圆台形底面直径φ=1 800mm，顶面为直径φ=750mm。为避免边界条件对抗拖网海床基周围流场产生影响，本文采用较大模拟计算空间，计算流域设置为长20m、宽8m、高8m的长方形。

图1 四棱台形抗拖网海床基外形图

图2 圆台形抗拖网海床基外形图

2.2 网格划分

将之前生成的几何模型导入到ICEM CFD中，设定整体网格尺寸，生成三维结构网格，并对海床基表面的网格进行加密处理，得到的网格单元总数分别为：四棱台型是33万个左右，圆台型是34万个左右。划分完网格之后的效果如图3和4所示。

3 Fluent分析设置

3.1 边界条件

求解器选取三维基于压力基隐式求解器；对动量方程和标量输运方程采用欠松弛技术，从而使得求解易于收敛，同时保证数值的稳定性；N-S方程采用有限体积法求解，采用SIMPLE方法进行压力速度耦合，时间采用一阶隐式，空间离散采用二阶迎风格式[6-8]。

由于海水流速受季节、潮汐及深度等多方面的影响，参照文献[9]，对海水的模拟速度进行选择。

图3 四棱台形抗拖网海床基计算流域与周围网格示意图

图4 圆台形抗拖网海床基计算流域与周围网格示意图

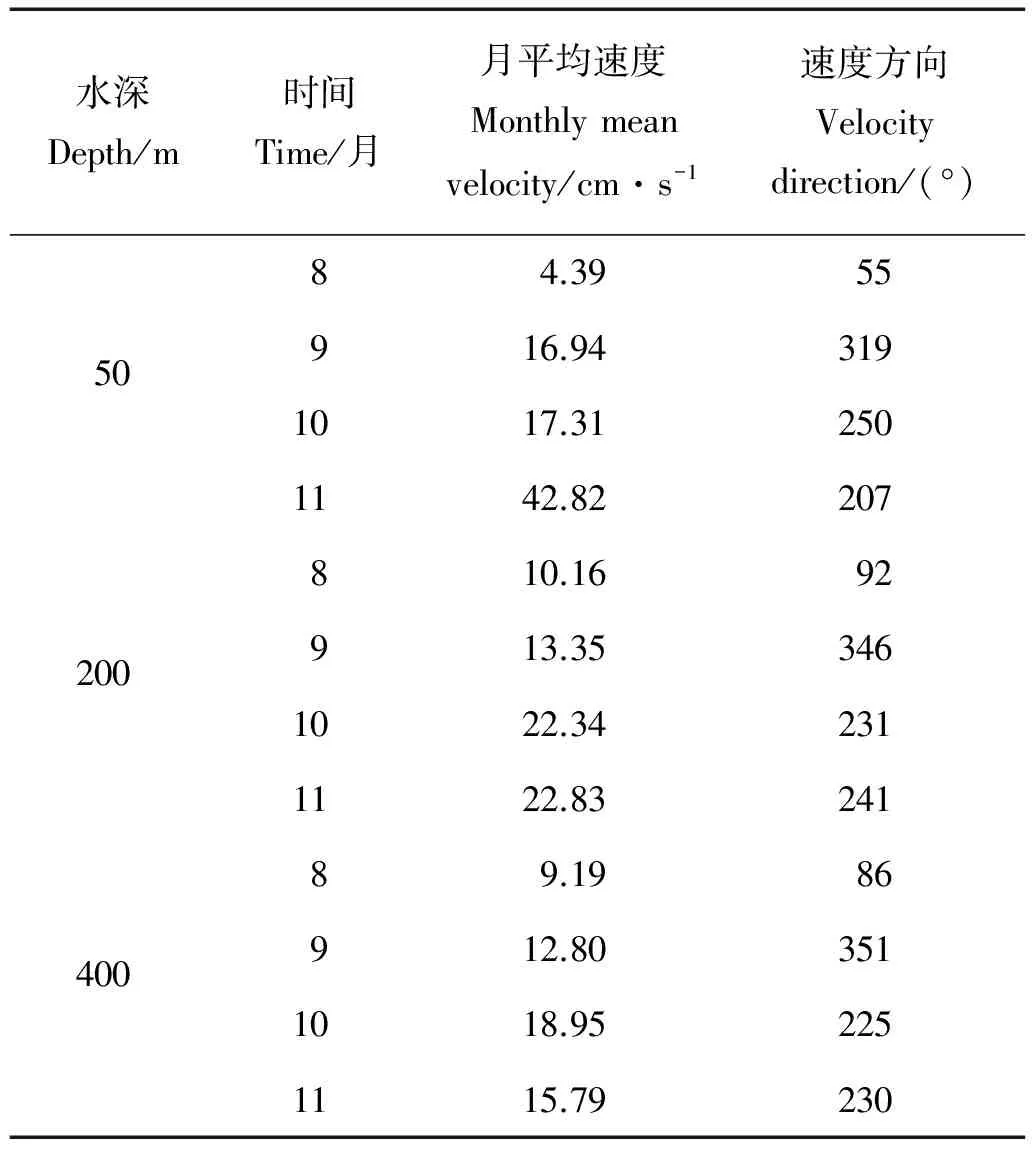
水深Depth/m时间Time/月月平均速度Monthlymeanvelocity/cm·s-1速度方向Velocitydirection/(°)5084．3955916．943191017．312501142．82207200810．1692913．353461022．342311122．8324140089．1986912．803511018．952251115．79230

为了充分研究海床基在不同深度下海水流速的作用，分别选取50、200及400 m 3个不同水域下的最大流速进行研究。为了分析方便，对3种水深下流速进行适当调整。

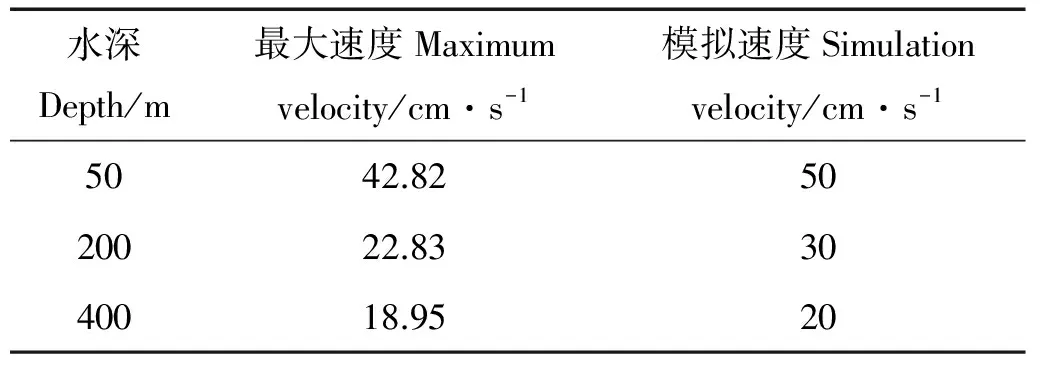
表2 入口速度

出口速度：由于出口上的流动接近完全发展，出口处的流速和压力为未知量，故采用outflow边界条件。

3.2 流固耦合分析

流固耦合的力学分析是流体力学与固体力学交叉而衍生的一门力学分支，是研究变形固体在流场作用下的各种行为以及固体变形对流场影响两者相互作用的一门学科[10]。流固耦合分析有单向耦合分析[11]和双向耦合分析[12]两种。其分析流程如下所示。

双向流固耦合较单向流固耦合更加全面，其可以分析流体流动的压力作用于海床基而产生的变形及海床基由于变形对于流体流道的影响两方面问题。但是其计算量大，分析效率较低。所以在分析时要根据实际情况合理选择耦合方式。

图5 单向流固耦合分析

图6 双向流固耦合分析流程

图7 单向耦合状态

图8 双向耦合状态

上图为圆台形海床基在不同耦合状态下的变形图，单向耦合状态下海床基的变形为，双向耦合状态下的变形为。由分析结果可以看出，两种状态下海床基的变形量的仿真结果基本相同，同时海床基在海流状态下的变形非常小，海床基的变形对海流的作影响较小。所以综合分析数据，为了加快分析结果，提高分析效率，本次模拟选择单向流固耦合方法。

3.3 动网格设置

动网格技术主要运用于运动边界问题，可以计算边界发生形变的问题。边界的形变过程可以使已知的，也可以是取决于内部流场变化。动网格的计算方法有3种，即弹簧光滑法(Spring-base Soothing)、动态层技术(Dynamic layering)和局部网格重画法(Local remeshing)[13]。由于弹簧光滑模型原则上可以用于任何一种网格体系，且设置方便，本文动网格技术选择弹簧光滑法。

在Dynamic mesh动网格设置面板中设置海床基表面为System Coupling，两侧壁面选择Deforming。

4 两种海床基外部流场分析结果及对比分析

4.1 速度场

以海水流速为0.5 m/s为例分析2种不同形式的海床基速度场，图9和10分别为四棱台形和圆台形抗拖网海床基周围海流速度矢量图。图中矢量箭头表示海流的流动方向，方向由左到右，由图中能够看出，海流在流动方向上因抗拖网海床基的阻碍作用，流速在抗拖网海床基迎流面上的底部区域有明显的下降，且速度最小，分别为7.99×10-3m/s(四棱台形)和9.95×10-3m/s(圆台形)。

海床基布放到海底之后会对整个区域产生一定的压缩，从而导致在抗拖网海床基两侧以及顶部区域的海流流速加快，在海床基迎流面上边缘区域出现最大值，分别为0.770 7 m/s(四棱台形)和0.71 m/s(圆台形)。比较两图得知，在同样海流作用下圆台形结构的抗拖网海床基周围海流速度的最大值比四棱台型结构要小很多，在相同尺寸情况下，可以将湍流的影响降至最小。

图9 四棱台形抗拖网海床基周围海流速度矢量图

图10 圆台形抗拖网海床基周围海流速度矢量图

4.2 压力场

四棱台形和圆台形抗拖网海床基外表面以及周围床面上在0.5海水流速下的压力云图分别如图11和12所示。图中显示四棱台形和圆台形抗拖网海床基所受最大压力分别为204和164 Pa，最大压力出现在抗拖网海床基迎流面的底部，该区域同时也是海流流速最小的地方。

四棱台形和圆台形所受最大负压分别为-226和-150 Pa，出现在抗拖网海床基的迎流面与背流面顶部，此处即为海流流速最大处。比较两图得知，圆台形的结构要比四棱台型的承受的压力小，从而减少受海流作用产生的位移。

图11 四棱台形抗拖网海床基表面压力云图

图12 圆台形抗拖网海床基表面压力云图

4.3 海床基底部流场分析

由于海床基布放于海底，且海床基底部设计有防沉地脚，布放过程中海床基底部可能与海底存在非常小的间隙，按照实际情况进行模拟很难对底部流场进行清晰的展示。所以为了研究海床基底部压力场的分布，对海床基底部流域做适当的放大，模拟结果如下所示。

图13 底部流场分析

从上图可以看出，海床基涡流发生区域均为尾部区域，且四棱台海床基比圆台形海床基更易出现涡流现象，四棱台海床基尾部涡流区域更大、更明显，大的涡流会出现底部泥沙掏空，影响海床基坐底的平稳性，所以进一步证明了圆台形海床基在控制局部海水流速方面的优势。

4.4 数据对比

圆台形和四棱台形抗拖网海床基在3种海流作用下速度和压力对比见表3。从3种深度下海床基模拟结果可以看出，在不同流速下圆台形海床基与四棱台形海床基压力及速度的改变趋势相同，圆台形海床基在局部应力控制方面优于四棱台。

表3 四棱台形和圆台形的海床基外部流场模拟数据对比

5 结语

通过SolidWorks建立了圆台形和四棱台形2种抗拖网海床基的CFD模型，通过对流固单向耦合和流固双向耦合的比较，选择了单向耦合方式分析海床基外部流场。通过模拟分析，得到了2种不同外形的抗拖网海床基周围海流速度场和表面压力场的分布图。通过比较2种外形结构的抗拖网海床基的流场分析结果，得知圆台形结构抗拖网海床基布放到海底后受到底流作用的影响较小，具有更高的稳定性，在局部应力控制方面效果更优。

此外，通过本文的研究希望能够为抗拖网海床基结构优化设计和实际应用提供理论参考。

[1] 孙思萍. 海床基海洋环境自动监测系统[J]. 海洋技术, 2000, 19(4): 1-7. SUN Si-ping. Seabed-base marine environment autornatic monitoring system[J]. Journal of ocean technology, 2000, 19(4): 1-7.

[2] WilliamJ, Teague, Dong S KO, et al. Currents Through the Korea/Tsushima Strait[J]. Oceanography , 2006, 19(3): 50-63.

[3] Deep Water Buoyancy. Trawl-Resistant Bottom Mounts[EB/OL]. [2014-04-15], [2014-10-20]. http:∥deepwaterbuoyancy.com/products/

[4] 张兆顺. 湍流[M]. 北京: 国防出版社, 2002. ZHANG Zhao-shun. TURBULENCE[M]. Beijing: National Defend Industry Press, 2002.

[5] 王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG Fu-jun. Computational Fluid Dynamics Analysis-The Principle and Application of CFD Software[M]. Beijing: TSINGMUA UNIVERSITY PRESS, 2004.

[6] 刘杰, 吴承璇, 吕斌, 等. 基于CFD的海床基观测平台外部流场分析[J]. 山东科学, 2012, 25(1): 65-68. LIU Jie, WU Cheng-xuan, LV Bin, et al. CFD based flow field analysis of a seabed monitoring platform[J]. 2012, 25(1): 65-68.

[7] 劳尔平, 齐梅兰. 水下淹没建筑物局部流场数值模拟及河床冲刷分析[J]. 水动力学研究与进展, 2007, 22(1): 99-105. LAO Er-ping, QI Mei-lan. Numerical simulation on local scour at downstream of submerged constructions[J]. Journal of Hydrodyn Amics, 2007, 22(1): 99-105.

[8] 徐天茂, 张立翔, 何士华. 基于微分求积法的三维非恒定、不可压N-S方程的数值计算模型[J]. 昆明理工大学学报(理工版), 2005(8): 63-68. XUTian-mao, ZHANG Li-xiang, HE Tai-hua. Numerical computation model of unsteady 3D incompressible navier-stokes eguations by differential ouadrature[J]. Journal of Kunming University of Science and Technology, 2005(8): 63-68.

[9] 袁耀初, 赵进平, 王惠群, 等. 南海东北部450 m以浅水层与深水层海流观测结果及其谱分析[J]. 中国科学(D辑), 2002, 32(2): 163-176. YUAN Yao-chu, ZHAO Jin-ping, WANG Hui-qun, et al. Observation results and spectral analysis of 450 m in the northeastern part of the South China Sea on the shallow water and deep water layers[J]. Science in China (Series D), 2002, 32(2): 163-176.

[10] 许进峰. ANSYS Workbench 15. 0完全自学一本通[M]. 北京: 电子工业出版社, 2014. XU Jin-feng. ANSYS Workbench 15. 0 Fully Self Taught a Pass[M]. Beijing: Publishing House of Electronics Industry, 2014.

[11] 朱利, 杨昌明, 郑军, 等. 基于流固耦合的轴流泵叶轮结构分析[J]. 流体机械, 2013, 41(3): 20-23. ZHU Li, YANG Chang-ming, ZHENG Jun, etal. Structure analysis of axial flow pump impeller based on fluid-solid coupling[J]. Fluid Machinery, 2013, 41(3): 20-23.

[12] 马富银, 吴九汇, 王广基. 双向流固耦合动态换热的分析方法[J]. 应用力学学报, 2013, 30(6): 894-898. MA Fu-yin, WU Jiu-hui, WANG Guang-ji. Double-sided fluid-structure coupling dynamicthermal analysis method[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 894-898.

[13] 周俊杰, 徐国权, 张华俊. FLUENT工程技术与实力分析(下册)[M]. 北京: 中国水利水电出版社, 2013. ZHOU Jun-jie, XU Guo-quan, ZHANG Hua-jun. Analysis of FLUENT Engineering Technology and Strength (2)[M]. Beijing: China Water & Power Press, 2013.

责任编辑 陈呈超

CFD Fluid-Structure Coupling Based Numerical Simulation Analysis of Exterior Flow Field on Deformed Trawl Resistant Seabed Basement

YU Kai-Ben1,2, LIU Bao-Hua2, YANG Tao3, GAO Jian3, LI Zheng-Guang2

(1.Ocean University of China, Qingdao 266100, China; 2.National Deep Sea Center, Qingdao 266061, China; 3.Qingdao Science & Technology University, Qingdao 266061, China)

In this paper, the fluid structure interaction analysis is carried out on two different shapes of trawl resistant seabed basement under the condition of considering the coupling field by using the computational fluid dynamics method (CFD). Firstly, according to the shape structure of trawl resistant seabed basement, we established the CFD models of the flow field, performed its pretreatment by using ICEM CFD software, and set the boundary conditions of the simulated area by dynamic grid technique. The method of unidirectional fluid structure interaction is selected according to the instruction and simulation of two kind of different coupling modes. Studied the numerical simulation results about two kind of trawl resistant seabed basement in velocity and pressure. This research can provide reference for the further optimization about structure design of seabed basement.

CFD； fluid-structure coupling； seabed basement； flow field； numerical simulation

海洋公益性行业科研专项经费项目“海洋污染过程监测集成与氮磷承载量评估技术子项目‘海床基监测系统集成技术研发’”(200905007-5)资助 Supported by Marine Public Welfare Industry Research Special Funds Project“Marine Pollution Process Monitoring Integration and Nitrogen and Phosphorus Carrying Capacity Evaluation Technology Sub Project ‘Research and Development of Integrated Technology of Seabed Based Monitoring System’”

2015-03-12；

2015-11-12

于凯本(1977-)，男，高级工程师，主要研究方向为海洋监测技术。E-mail: yukb@ndsc.org.cn

P715.5

A

1672-5174(2017)01-105-06

10.16441/j.cnki.hdxb.20150112

于凯本， 刘保华， 杨涛， 等. 基于流-固耦合的不同外形抗拖网海床基外部流场分析[J]. 中国海洋大学学报(自然科学版), 2017, 47(1): 105-110.

YU Kai-Ben, LIU Bao-Hua, YANG Tao， et al. CFD fluid-structure coupling based numerical simulation analysis of exterior flow field on deformed Trawl Resistant Seabed Basement[J]. Periodical of Ocean University of China, 2017, 47(1): 105-110.