某弹用电子部件贮存寿命评估
2017-01-06
(海军驻重庆地区导弹设备军事代表室,重庆 402760)
某弹用电子部件贮存寿命评估
丰雷
(海军驻重庆地区导弹设备军事代表室,重庆 402760)
目的研究使用定时截尾步进应力加速寿命试验方法评估某弹用电子部件在一定可靠度下的贮存寿命。方法首先将其在应力Si(i>1)下的作用时间全部转化为在应力S1下的等效作用时间,然后建立威布尔分布加速寿命模型,采用Newton-Raphson方法求解似然方程,得到模型未知参数的极大似然估计结果,最后外推得到正常温度下的贮存寿命。结果在25 ℃下可靠度为0.9999时,使用定时截尾步进应力加速寿命试验方法评估电子部件的寿命约为 11.89年,使用恒定应力加速寿命试验评估寿命为13.32年,两种试验方法的评估结果相差不大。结论步进应力加速寿命试验时间短、样本量少、成本低,相对于恒定应力加速寿命试验方法,具有一定的优越性。
电子部件;步进应力;Newton-Raphson方法;寿命评估
某弹用电子部件主要完成解保及起爆功能,是保证弹药使用安全性和可靠性的关键部件,其贮存寿命直接影响弹药系统的贮存寿命,因此评估其贮存寿命具有重要的现实意义。
由于其长寿命、高可靠的特点,采用自然环境贮存寿命试验周期长、成本高,加速寿命试验的方式可快速获取其贮存寿命。常用的加速寿命试验主要有恒定应力加速寿命试验、步进应力加速寿命试验及序进应力加速寿命试验。由于步进应力加速寿命试验在对试验设备要求、样本量及试验时间上具有优势,因此采用步进应力加速寿命试验获得电子部件常温贮存寿命。
威布尔分布[1]和指数分布[2]是两种常用于描述电子部件寿命分布情况的统计分布模型,当威布尔分布形状参数为 1时,即为指数分布。针对基于威布尔分布条件下的加速寿命试验数据处理,王玲玲[3]采用罗伊登(Broyden)法对最大似然函数未知参数进行求解;徐晓玲[4]采用逆矩估计法进行统计分析;文献[5]得到了基于二项分布的样本似然函数;胡恩平[6]采用拟牛顿法对含有位置参数的超越方程组进行求解;李凌[7]针对定数截尾场合下建立了威布尔寿命步进应力加速寿命模型,利用Newton-Raphson方法求解似然方程,并基于失效数统计规律给出了一种精度更高的初值确定方法。
文中在前述文献基础上,基于某弹用电子部件定时截尾步进应力加速寿命试验,建立了加速寿命模型,未知参数的计算采用Newton-Raphson方法,针对参数初值的敏感性问题[8—9],提出了一种基于最低应力寿命数据的初值选取方法,选取的初值更加有效快捷,也具有较好的收敛效果。
1 加速寿命试验设计
1.1 试验方案设计
文献[9]指出,在仓库贮存条件下,影响导弹贮存寿命的主要因素为温度,因此选用温度应力作为其加速应力,通过前期温度冲击试验掌握电子部件的温度响应情况,最终得到了该电子部件的工作极限温度应力为 180 ℃,极限破坏温度应力为185 ℃。
根据可靠性原理,在进行步进应力加速寿命试验时,加速应力水平的个数不少于 3个,故取加速应力水平数为3。适当选择应力水平的间隔,确定3组温度应力分别为θ1=155 ℃,θ2=165 ℃,θ3=175 ℃。结合样本量、应力转换时间点、应力检测次数等其他试验相关参数,整个试验方案见表1。

表1 试验方案Table 1 Test scheme
1.2 试验实施过程
从一批产品中随机选取n个试验样品,测量并记录电子部件初始条件下各参数后,将其全部置于θ1下进行寿命试验。在θ1应力下对电子部件输入电流、输入电压、输出电流、输出电压、自毁时间等性能参数检测 k1次,直到规定的试验时间τ1为止;再将应力提高到θ2,把未失效的样品放在θ2下继续进行寿命试验,直到τ2为止;随即将应力提高到θ3,把在前两个温度应力下都未失效的样品放在θ3下进行寿命试验,直到τ3为止试验结束。
2 加速寿命模型
2.1 基本假设
试验数据的统计分析与模型的推导均是在以下4个假定下进行的。
假定1:电子部件在正常贮存条件和加速应力下的寿命均服从两参数威布尔分布W(mi,ηi)[12-13];
假定2:在各试验温度应力下,产品的失效机理不变。由于威布尔寿命分布的形状参数m反映失效机理[6],因此m0=m1=m2=m3。
假定3:加速模型符合Arrhenius方程,即各温度应力下寿命分布的尺度参数ηi与应力水平θi满足关系式:

对等式两边取对数,且令ln(A)=a,-Ea/R=b,可得:

假定4:产品的剩余寿命仅依赖于已累计失效部分和当时的应力水平,而与累计方式无关(Nelson累积失效假定)。
2.2 寿命数据分析
由步进应力加速寿命试验的试验方法可知,在应力水平θi下的失效数据tij,除i=1外,并不是在应力水平θi下的真实寿命,因为在时间(τi-2,τi-1)产品经受的应力为θi-1,因此对试验时间进行折算。
根据假定4,在应力水平θi下,产品工作ti时间内累计失效概率Fi(ti)相当于在应力水平θj下工作tij时间内的累计失效概率Fj(tij),基于威布尔分布的分布函数可得:

由假定2可知mi=mj,由式(2)可得折算公式:

将加速模型(1)带入折算公式可得:



将其他应力下的失效时间全部折算到应力θ1下,折算系数为:

则折算后的失效时间为:

2.3 失效寿命的参数估计
利用折算公式得到应力水平1S下的数据是一组容量为n,取自威布尔分布W(m,η1)的定时截尾“样本”。实际上它不是真正的样本,而是通过时间折算公式计算后得到的数据,其中含有未知参数b,因无法用定时截尾试验样本的统计处理方法,现采用极大似然法[8,14]进行计算。

似然函数为:对似然函数取对数可得:

通过对对数似然函数求一阶偏导,并令其为0,即可得到各参数的极大似然函数点估计值。




Newton-Raphson法的收敛性和收敛速度与迭代初值的相关性较大,针对此种情况,考虑到产品的步进应力加速寿命试验中,应力θ1下得到的寿命为其真实寿命信息。因此首先采用基于威布尔分布的恒定应力加速寿命评估技术[10—11],获得应力下威布尔寿命分布的形状参数m0和位置参数η0,带入式(10)即可得到关于位置参数b的一元非线性方程,采用二分法即可得到参数b的初始迭代值b0,带入得到参数a的初始迭代值a0。由此得到Newton-Raphson算法的迭代初值x0=(m0,a0,b0)。
将迭代初值带入式(12),其中:

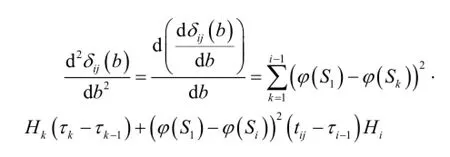
3 寿命评估
试验结束后,经统计分析,应力θ1下失效 3个,应力θ2下失效9个,应力θ3下失效6个。通过对应力θ1下的失效寿命进行计算得到,其寿命分布的形状参数m=4.6185,尺度参数η=999.37,带入式(10)得到参数b=6006.313,通过二分法求解可得Newton-Raphson算法迭代初值为x0=(4.6185, -7.1214, 6006.313)。通过多次迭代得到未知参数收敛 结 果 ,其 估 计值 为ˆ= 4.18,ˆ= -8.1540,= 6532.7332,迭代过程如图1—3所示。

图1 参数m的迭代过程Fig.1 The iterative process of parameter m

图2 参数a的迭代过程Fig.2 The iterative process of parameter a
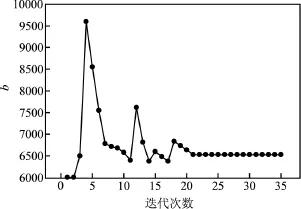
图3 参数b的迭代过程Fig.3 The iterative process of parameter b
因此,电子部件的特征寿命η与所加的温度应力水平θ满足加速寿命方程:

由式(13)可以得到25 ℃下的寿命分布尺度参数为9.4303×105,20 ℃下的寿命分布尺度参数为1.3704×106,可靠度函数如图4所示。

图4 电子部件可靠度曲线Fig.4 The reliability curve of electronic components
由图4可得,对应可靠度下的寿命见表2。
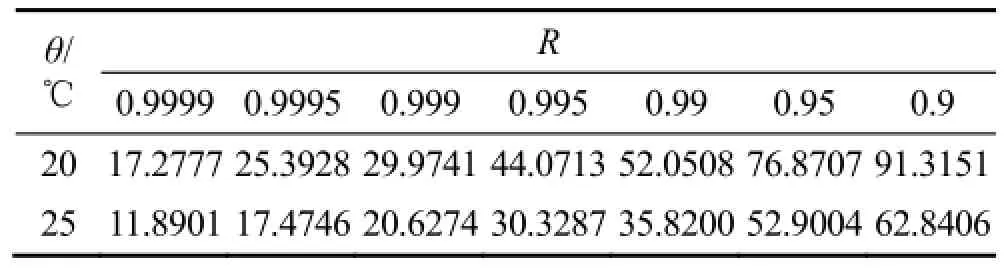
表2 不同可靠度下的寿命估计Table 2 Life assessment under different reliability
由表2可知,在25 ℃下可靠度为0.9999时,电子部件的寿命约为11.89年。在前期进行的电子部件恒定应力加速寿命试验结果表明,电子部件在可靠度为0.9999时,其贮存寿命为13.32年。由此可见,采用步进应力加速寿命试验的评估结果和采用恒定应力加速寿命试验的评估结果相差不大,然而步进应力加速寿命试验的试验时间短、样本量少、试验成本低,充分说明了步进应力加速寿命试验相对于恒定应力加速寿命试验的优越性。
4 结论
采用基于定时截尾步进应力的加速寿命试验方法获得了电子部件在高温应力下的失效寿命,建立了基于威布尔寿命分布的步进应力加速寿命模型。采用Newton-Raphson方法求解模型中的未知参数,并外推得到电子部件在常温下的贮存寿命。通过与恒定应力加速寿命试验结果对比,充分说明了步进应力加速寿命试验相对于恒定应力加速寿命的优越性,同时可以对其他电子产品贮存寿命评估起到一定的参考和借鉴作用。
[1] 刘秀萍. 电子产品的加速贮存可靠性模型及统计分析[D]. 贵阳: 贵州大学, 2007. LIU Xiu-ping. Accelerated Storage Reliability Model and Statistical Analysis of Electronic Products[D]. Guizhou: Guizhou University, 2007.
[2] 赵宇. 可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2009. ZHAO Yu. Reliability Data Analysis Tutorial[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2009.
[3] 王玲玲. 步进应力加速寿命试验数据处理及其应用[J].数理统计与管理, 1984(1): 20—25. WANG L L. Step Stress Accelerated Life Test Data Processing and Application[J]. Applications of Statistics and Management, 1984(1): 20—25.
[4] 徐晓岭, 费鹤良. 威布尔分布场合下步进应力加速寿命试验的统计分析[J]. 运筹学学报, 1999(3): 73—84. XU Xiao-lei, FEI He-liang. Statistical Analysis of Accelerated Life Testing-step-stress Models under the Weibull Distribution Case[J]. OR Transactions, 1999(3): 73—84.
[5] 李淦, 郑波. 基于步进应力加速寿命试验的某新型弹药储存寿命评估[J]. 弹箭与制导学报, 2007, 27(2): 307—308. LI Gin, ZHENG Bo. The Estimation of an New-style Ammunition Storage Life Based on the Test of Stepping Stress Acceleration Life[J]. Journal of Missile and Guidance, 2007, 27(2): 307—308.
[6] 胡恩平, 罗兴柏, 艾志利. 三参数威布尔分布条件下的无线电引信步进应力加速寿命试验与数据处理[J]. 探测与控制学报, 2000, 22(2): 37—40. HU En-ping, LUO Xing-bai, AI Zhi-li. The Step Stress Altand Data Processing of the Radio Fuze under the Condition of Three-parameter Weibull Distribution[J]. Journal of Detection & Control, 2000, 22(2):37—40.
[7] 李凌, 徐伟. 威布尔产品加速寿命试验的可靠性分析[J].系统工程与电子技术, 2010, 32(7): 1544—1548. LI Ling, XU Wei. Reliability Analysis for Accelerated Life Test Based on Weibull Distribution[J]. Systems Engineering and Electronics, 2010, 32(7): 1544—1548.
[8] BALAKRISHNAN N, XIE Q. Exact Inference for a Simple Step-stress Model with Type-I Hybrid Censored Data from the Exponential Distribution[J]. Journal of Statistical Planning & Inference, 2007, 137(8):2543—2563.
[9] YAO J, MINGGE X U, ZHONG W, et al. Research of Step-down Stress Accelerated Degradation Data Assessment Method of a Certain Type of Missile Tank[J]. Chinese Journal of Aeronautics, 2012, 25(6): 917—924.
[10] 湛远礼, 罗红. 恒定应力加速寿命试验模型及应用——威布尔分布[J]. 自动化与仪器仪表, 2009(6): 48—50. ZHAN Yuan-li, LUO Hong. Constant Stress Accelerated Life Test Model and Its Application—Weibull Distribution [J]. Automation and Instrumentation, 2009(6): 48—50.
[11] 茆诗松, 韩青. Weibull分布定时截尾样本下寿命试验与加速寿命试验的统计分布[J]. 应用概率统计, 1991(1): 61—72. MAO Si-song, HAN Qing. Statistical Analysis of Life and Accelerated Life Test on Weibull Distribution Case under Type Censoring [J]. Applied Probability and Statistics, 1991(1):61—72.
[12] 费鹤良. 威布尔分布和正态分布参数估计方法综述[J].数理统计和应用概率, 1984(2) : 115—126. FEI He-liang. The Weibull Distribution and Normal Distribution Parameter Estimation Methods . Mathematical Theory and Applied Probability, 1984(2) : 115—126.
[13] 施庆生. 概率论与数理统计[M]. 北京:化学工业出版业, 2008. SHI Qing-sheng. Probability Theory and Mathematical Statistics[M]. Beijing: Chemical Industry Press, 2008.
[14] 杨谋存, 聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报, 2007, 39(1): 22—25. YANG Mou-cun, NIE Hong. Maximum Likelihood Parameter Estimation of Three Parameter Weibull Distrition Numerical Solution[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2007, 39(1): 22—25.
Storage Life Assessment of Electronic Component in a Missile
FENG Lei
(Navy Military Representative Office of Missile Equipment in Chongqing Area, Chongqing 402760, China)
The paper aims to estimate the storage life of electronic components in a missile under a certain degree of reliability based on censoring data from step-up-stress accelerated life test. First, the testing time under the stress of Si(i>1) was converted to the equivalent time under the stress S1. Then, a Weibull step-up-stress accelerated life test model was established and the Newton-Raphson method was applied to solve the likelihood equation. At last, the storage life at normal temperature was estimated according to the MLE result of unknown parameters in the model. When the reliability was 0.9999 at 25 degrees Celsius, the storage life of electronic components based on censoring data from step-up-stress accelerated test was about 11.89 years, and the life based on constant-stress accelerated test was about 13.32 years. The evaluation results of the two test methods were not quite different. Step-up-stress accelerated life test time is short, the sample is small and the cost is low. It has certain superiority compared with constant-stress accelerated test.
electronic components; step-up-stress; Newton-Raphson method; lifetime assessment
10.7643/ issn.1672-9242.2016.06.020
TJ81;TG174.4
A
1672-9242(2016)06-0114-06
2016-06-24;
2016-07-26
Received:2016-06-24;Revised:2016-07-26
丰雷(1980—),男,湖南人,硕士,工程师,主要研究方向为武器装备质量监督。
Biography:FENG Lei(1980—), Male, Hunan, Master, Engineer, Research focus: quality supervision of weapons and equipment research.
