老题新谈——一次关于“SSA”的活动课

江苏省南京市科利华中学 董秀明

老题新谈
——一次关于“SSA”的活动课

江苏省南京市科利华中学 董秀明

刚刚学完八上第一章“全等三角形”，我和孩子们迫不及待地想去解决前面遗留的一个问题，那就是两边分别相等且其中一对等边的对角也相等的两个三角形全等吗？为此，我在班级开设了一节组内公开课，我把这节课定位为一节活动课。

下面展示一下课堂活动全过程。（事先，学生已经准备好白纸和作图工具，我事先将班级分成了7个小组，每个小组6 人，方便后面的分组活动）

师：前面我们在探索三角形全等的条件时，对于第一个条件“SAS”，课堂上老师反复强调这里的“角”必须是两边的夹角，而不能是一对相等边的“对角”，也就是不能说成“SSA”，现在学完了这一章，同学们有什么想法呢？

生1：我觉得“SSA”不能说一定错，它也有对的时候，比如我们学的“HL”定理，其实就是；两个直角三角形满足“SSA”，但是这两个直角三角形是全等的。

生2：我同意上面的说法，其实我们平时经常做到一个选择题，已经给了图形，比如两个同为锐角三角形，我觉得此时“SSA”的条件也对，我们上次几个同学们还一起证明出来了呢！

生3：我们前面做过评价手册上的一道画图题（该生直接拿出评价手册），在P23的第5题，那道题目就是提供的“SSA”的条件，但是我们可以画出两个不同形状的三角形，这时候两个三角形不全等。

此时，我正观察全班同学，我看到很多同学纷纷点头。

生4：我们小组一起讨论过这个问题，我们发现了一个结论：“HL”之所以对，是因为直角是直角三角形中最大的角，只要“SSA”中的“角”是三角形中最大的角，此时若满足“SSA”，那这两个三角形一定全等。

师：好的，同学们在课后做了很多的探索，非常好！现在我们发现不能一棍子把“SSA”打死了，我们只能说“SSA”不一定对。那今天这节课，我们给大家一些“SSA ”的条件，请同学们自己来画图，看看有什么新的发现，能否对“SSA”认识得更加清晰一些！

师：为了同学们画图的方便，我给同学们的讲义上提供的△ABC是三个角分别是30度，45度，105度的一个三角形。

师：请同学们利用“SSA”画△DEF，我们一起来看看同学们画的△DEF和△ABC是否全等。我们先提供这样一组“SSA”的条件：∠D=∠A，DE=AB，EF=BC。

（同学们画图）图形如下：

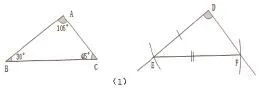
师：此时两个三角形全等吗？

生异口同声：全等。

师：那同学们能否再提供一组“SSA”的条件呢？

生5：∠D=∠A，DF=AC，EF=BC。

生6：∠E=∠B，DE=AB，DF=AC。

师：好的，下面我们分组，请每个小组先把所有的情况分类好，然后每个成员完成其中的一种情况。（小组开始讨论并分工合作）

大约5分钟之后，我和同学一同汇总了所有情况的图形，图形如下：

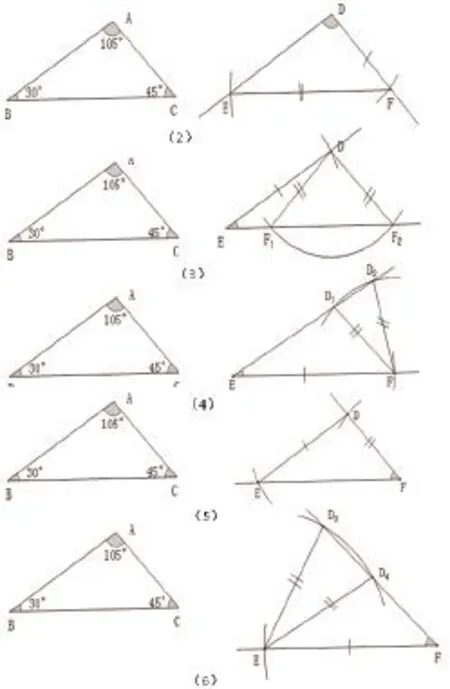
师：为了同学们比较的方便，我们把同学们刚才画的各种情形绘成一个表格吧。

（我现场板书表格，如下图）

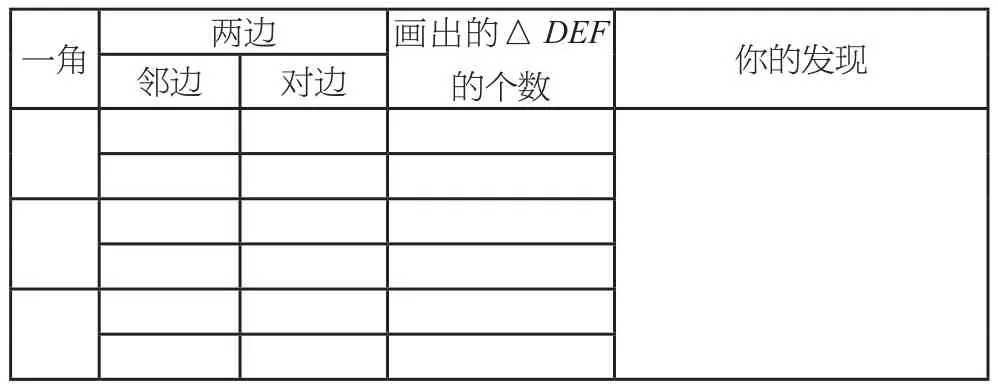
一角 两边 画出的△DEF的个数 你的发现邻边 对边

我们请一个组的同学上来填写这个表格。我们先填写表格的前三列。

（6名同学上来将表格填写完整，如下图）

一角 两边 画出的△DEF的个数 你的发现邻边 对边∠D=∠ADE=ABEF=BC 1个 （和△ABC全等）DF=AC EF=BC 1个 （和△ABC全等）∠E=∠BDE=ABDF=AC2个（其中一个和△ABC全等，另一个和△ABC不全等）EF=BC DF=AC2个（其中一个和△ABC全等，另一个和△ABC不全等）∠F=∠CDF=AC DE=AB 1个 （和△ABC全等）EF=BC DE=AB2个（其中一个和△ABC全等，另一个和△ABC不全等）

师：请同学们根据你画的图形和表格的填写，说出你有什么发现？

1分钟后，同学们都没有发表意见，或许是觉得自己说得不够好，或许是自己还没有感受到什么发现。我决定让学生继续用同样的方法探究锐角三角形的情况。（当时讲义上事先并没有准备锐角三角形的情况）

师：下面请每位同学在讲义下面的空白处画一个锐角△ABC，使得∠A=45度，∠B=60度，∠C=75度，请同学们按照我们刚才的探索方式，小组分工合作，继续探索“SSA”。

同学们开始忙碌起来，我在同学们周围巡视。

大约5分钟之后，小组进行了汇报，图形如下：

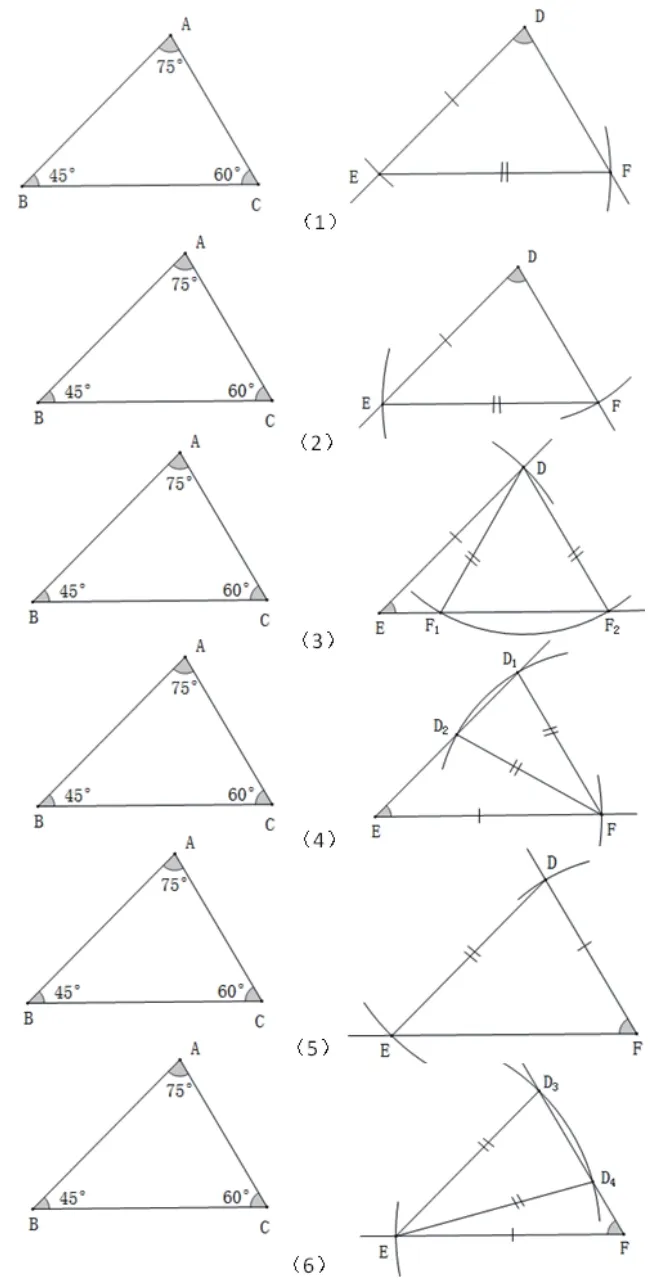
（小组同学也已经模仿讲义上的表格绘制了锐角三角形的对应的各种情形，表格如下）

一角 两边 画出的△DEF的个数 你的发现邻边 对边∠D=∠ADE=AB EF=BC 1个 （和△ABC全等）DF=AC EF=BC 1个 （和△ABC全等）∠E=∠BDE=AB DF=AC2个（其中一个和△ABC全等，另一个和△ABC不全等）EF=BC DF=AC2个（其中一个和△ABC全等，另一个和△ABC不全等）∠F=∠CDF=AC DE=AB 1个 （和△ABC全等）EF=BC DE=AB2个（其中一个和△ABC全等，另一个和△ABC不全等）

师：很好，同学们在较短的时间内分工合作，表格完成得很好，现在就请同学们动脑筋想一想，通过两次探究，你有些什么想法？小组内可以互相讨论。

3分钟左右，已经有小组同学跃跃欲试，我请同学汇报他们的发现。

组1：我们组发现的结果是这样：如果两个三角形满足最大的角对应相等，无论是锐角三角形还是钝角三角形，“SSA”都是成立的，也就是说，两个三角形一定是全等的。

组2：我们组是通过表格中边的关系找到了规律，我们发现当“SSA”中的角的对边大于或等于邻边时，“SSA”成立，两个三角形一定是全等的，反之，不一定全等。

组3：我们组和前面第一个组的发现差不多，不过我们还发现了，如果是最小的角对应相等，“SSA”一定不成立，也就是根据“SSA”一定能画出两个三角形，其中一个和原来的三角形全等，另一个和原来的三角形不全等。如果这个角既不是最大的角也不是最小的角，那么“SSA”不一定成立。

师：好的，同学们经过合作讨论，有这么多好的发现，太棒了！有的组从“角”出发考虑，有的组想到了对边和邻边的关系，也发现了其中的规律。为了验证同学们的发现，谁再来出一道题好不好？（在此刻的课堂上，我感动于孩子们的探究和发现，也相信孩子们能够现场提出问题。）

生7：在△ABC和△DEF中，∠A=∠D=95°，AB=DE，BC=EF，△ABC和△DEF全等吗？

生8：我就是把刚才的角度修改一下，改成∠A=∠D=50°。（这里为了看起来清晰，我把这位同学的回答补充成完整的题目：在△ABC和△DEF中，∠A=∠D=50°，AB=DE，BC=EF，△ABC和△DEF全等吗？）

师：好的，由于时间关系，同学们课后可以通过画图验证，再结合今天同学们的发现，看看大家的发现是否都是正确的。

师：这里补充说明，第二个发言的小组发现了表格里角的对边和邻边的关系，很精彩，将来待同学们到初三的时候学到“锐角三角函数”就可以解释了！

师：今天这节数学活动课同学们表现得非常棒，“SSA”是一个老问题，但是我们经过安排这一节活动课，同学们有了更深度的思考，有了更全面的、更新的认识和发现，正所谓“老题新谈”！好，下课！

虽然课已结束，但是从同学们的表情可以看出，大家“意犹未尽”！

二、教学反思

本次“数学活动”基于学生已有的“三角形全等的条件”的知识和相关尺规作图的经验，让学生进行动手实践和探索活动。本次“数学活动”不像其他数学活动一样都有一个特定的目标，而是以“SSA”为载体，让学生在活动中不断地经历“分析问题—解决问题—发现问题—提出问题”的四能学习要求，使知识的本质、经验的运用和思维的迁移充分得到体现！

本次活动的重点不在于学生是否将满足“SSA”的两个三角形“证明”出全等，学生能够感悟到本次活动的数学知识及其本质；能够通过画图操作，验证思考的正确性,积累活动经验；通过操作交流合作，激发学生探究的兴趣，渗透解决问题的策略和数学思想，进一步提升创新思维能力。

教学相长，一次数学活动使得笔者对学生的学习潜能有了新的认识，对“数学活动”的内涵有了更为深刻的理解。“数学活动”要基于数学体验，关注形成和发现过程；立足数学认识，关注猜想和说理过程；把握数学本质，关注揭示和归纳过程；突出数学探究，关注应用和创新过程；提升数学素养，关注反思和积累过程。