一元二次方程中的易错题型小结

江西省赣州中学 黄学财

一元二次方程中的易错题型小结

江西省赣州中学 黄学财

数学是每一名学生都想学好的学科，每个人的理解能力不一致，加上其他的一些因素，能把数学学得溜的学生不是特别多。在解数学问题时，会而不对、对而不全这种现象十分普遍，对于优生来讲如何减少失误，发挥最大潜力，即减少非智力因素带来的影响，是他们很关心的问题。解决这个问题的法宝，就是多总结，尤其是易错题，要多归类，列出易错的知识点，举一反三，达到触类旁通的目的。

一元二次方程；系数；实际问题

一元二次方程是初中阶段最难学的方程，也起着承上启下的作用，为后续高中学好二元方程打下扎实的基础。一元二次方程重点在于它的解法，从课本上看出，一元二次方程的解法由最简单的直接开平方法到因式分解法，层层推进，一元二次方程的解法还是有较多学生过不了关，出现的主要问题是公式不熟、符号问题、方法选择不恰当、未排根等，尤其是一元二次方程的综合运用问题，不仅考查学生的文字理解能力，更考查学生的运算与思维能力。为帮助学生在解一元二次方程的问题中少出错，特把一元二次方程中的易错题型进行小结，以飨读者。

一、忽视一元二次方程的二次项系数不为零

学习方程与函数类似，务必理解方程与函数满足的条件，即二次项系数不能为零，这是方程首先要满足的条件，这个条件不满足，就犹如没有母鸡哪来的鸡蛋。

二、确定一元二次方程各项的系数时，没有化成一元二次方程的一般形式，导致符号出现错误

确定方程各项的系数，必须把方程化成一般形式，即左边是关于未知数的代数式，右边是0，最好把二次项系数化成正整数，方便后面的计算。

三、不能完全理解用配方法解一元二次方程的原理

要熟练运用配方来解一元二次方程，就必须掌握好配方法的原理。配方法是由完全平方公式推导而来，可改为，让学生填空，学生容易填b2，可试着问填的常数与一次项系数有何关系？如果学生还理解不了，可举若干实例让学生理解。

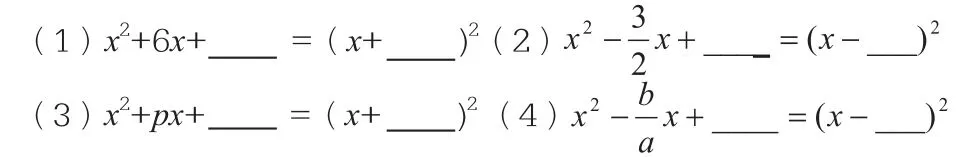
并观察这四个式子共同的特征，得出添加常数的结论。当x2项的系数不是1时，上述结论还成立吗？要求学生计算下列两个式子：

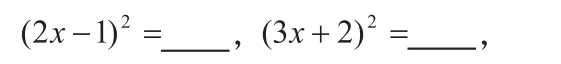
运用配方容易出现的错误是：1、二次项系数不是1时，两边除以二次项系数时出现错误；2、两边未同时加上所填的常数项；3、两边只是加了一次项系数的一半；4、所选的完全平方公式出错，正负不分。

四、运用根与系数的关系时混淆公式及忽视了Δ≥0

五、混淆实际问题中的单循环与双循环赛制

为让学生理解好单循环与双循环赛制区别，可举例说明：若有四个球队甲、乙、丙、丁，赛制为单循环形式（每两个球队之间要比赛一场）。对甲来说，甲要与乙、丙、丁各比赛一场，即甲要比赛三场；对乙来说，乙也要与甲、丙、丁各比赛一场，即乙要比赛三场；同理对丙、丁来说也要比赛三场，这样下来，整个比赛一共比赛了4（4个队）×3（每个队均要赛三场）＝12场，但细心的同学会发现比赛场数有重复，如甲与乙的比赛只能算一场，按上面的这种算法重复算了一次，所以总的比赛场数要除以2。

1.（2015·呼伦贝尔）学校要组织足球比赛，赛制为单循环形式（每两队之间赛一场），计划安排21场比赛，应邀请多少个球队参赛？设邀请x个球队参赛，根据题意，下面所列方程正确的是（ ）

2.某摄影小组互送相片作纪念，已知全组共送出相片132张，则该摄影小组有_______人。