大跨度连续梁转体施工平衡称重分析

2017-01-05王常峰

城市道桥与防洪 2016年12期

关键词：顶力摩阻转体

舒康，王常峰，秦凯

（烟台大学，山东烟台 264005）

大跨度连续梁转体施工平衡称重分析

舒康，王常峰，秦凯

（烟台大学，山东烟台 264005）

青连铁路工程牟家村跨同三高速公路特大桥，上跨兖日铁路，采用了转体的施工方法，在桥梁转体之前对转动体进行了称重试验以保证桥梁安全顺利转动。采用了平衡称重的试验方法，对测试结果进行了分析，提出了对转体梁的平衡配重方案，为正式转体牵引力大小的确定提供了基本参数。转体过程表明，桥梁的配重合适，桥梁转体过程进展顺利。

大跨度连续梁；转体施工；称重试验；不平衡力矩；配重

0 引言

随着我国交通运输业的飞速发展，各类型的跨线桥越来越多，桥梁转体施工方法在跨越既有线施工的同时又能保证既有交通运输的畅通，而且转体施工方法可以将在障碍上空的作业转换到无障碍一侧进行施工，极大地降低了施工难度，因而近年来转体施工也得到了快速推广[1]。为了使桥梁转体过程更加安全可靠，很多学者对桥梁转体之前的称重试验做了大量研究。魏峰、陈强、马林[2]提出球铰摩擦面简化为平面计算摩阻系数的条件。蔡军田[3]得出采用平衡称重和配重的方式，极大地减小转体所需的牵引力。尚高科[4]提出浇筑梁体挂篮拆除不对称时，在称重之前对梁体进行预配重。王继红[5]给出了弯斜T构的纠偏措施。宝成德、向中富[6，7]等提出，一个理想的转动体必须具备安全稳定和易于转动这两个基本条件。郭恒[8]提出球铰是整个转体系统最关键构件，摩阻系数直接影响着转体所需牵引力的大小。谭雷平[9]指出在大吨位拱桥转体施工中平衡称重试验数据能对施工起到较好的指导效果。对于转体梁而言，梁体混凝土分布差异（锯齿块分布不对称，桥梁纵坡以及混凝土浇筑过程中的误差）、边跨及中跨钢筋的用量不同、预应力张拉程度的差异等均会导致中跨及边跨梁体的自重和刚度不对称，从而产生不平衡力矩。为了保证连续梁始终能够保持安全、平稳，在梁体转动前必须对连续梁进行不平衡力矩测试试验（即称重试验）以确定连续梁转动过程中的受力状态，同时计算出转动体的摩擦系数、偏心距及不平衡力矩等参数，为后续转体过程选择机械设备、施工处理措施以及转体的安全性能评估提供必要的技术依据。本文以青连铁路牟家村跨同三高速公路（40+64+40）m连续梁桥转体施工为例，对转体梁的称重试验进行了论述。

1 工程概况

新建青连铁路工程ZQ-3标段牟家村跨同三高速公路特大桥（40+64+40）m连续梁桥上跨兖日铁路，为三跨混凝土连续梁桥，全桥长144 m，转体过程中采用两墩同步转体的施工方法。连续梁梁体为单箱单室、变高度、变截面直腹板结构。箱梁顶宽8.1 m，箱梁底宽4.4～5.4 m。全联在端支点、中跨中及中支点处共设5个横隔板，横隔板设有过人孔洞，供检查人员通过。顶板厚度除梁端外均为35 cm，底板厚度由跨中的40 cm按二次抛物线变化至根部的70cm，腹板厚40～60 cm、60～80 cm，按折线变化。梁体截面梁高最厚为5 m，最薄为3 m，按二次抛物线变化。

转体系统由上下转盘、球铰及动力系统组成。上转盘是转体的重要结构，在整个转体过程中形成多向、立体的受力状态，为八边形，高2.0 m；转台直径7.6 m，高度为0.8 m。下盘为支撑转体结构全部重量的基础，转体完成后与上转盘通过后封C50混凝土共同形成桥梁基础承台。上球铰直径4 200 mm，下转盘球铰直径3 000 mm，厚度均为40 mm。18#、19#转体墩总重量均为30 000 kN，转体角度为48°。两转体墩采用同步逆时针一次性转体到位。

2 称重分析方法

2.1 称重原理

（1）称重测试原理

该桥采用球铰转动法测试梁体不平衡力矩，这种方法是通过刚体位移突变来确定转动体的各种相关参数。此方法优点主要在于只考虑转体梁的刚体效应，排除了结构发生位移突变之前挠度等因素的影响，因而得出的结果较为准确[10]。连体在拆除支架和砂箱后，整个T构会出现两种情况的平衡方式，MZ定义为摩阻力矩，MG为不平衡力矩。两种平衡方式如下：

方式一：MZ＜MG，在此种情况下，梁体在不平衡力矩作用下会在竖平面内发生刚体转动直至撑脚与滑道面接触，此时撑脚参与受力。

假设重心在右侧：从大里程侧升顶时，P1L大-MG-MZ=0；从大里程测落顶时，P2L大-MG-MZ=0；。联立方程可求得：MG=（P1+P2）L大/2，MG=（P1-P2）L大/2。

方式二：MZ＞MG，这种受力状况下，结构摩擦力矩抵消了不平衡力矩，在竖平面内梁体不发生刚体转动，撑脚不会参与受力此状态称之为自平衡状态。

假设重心在右侧：大里程侧顶升时，P3L大-MGMZ=0；小里程侧顶升时，P4L大-MG-MZ=0。联立方程可求得：MG=（P3L大+P4L小）/2,MG=（P3L大-P2L小）/2。

（2）球铰摩擦系数计算原理

称重试验时，梁体在竖平面内发生顺时针、逆时针的微小转动。摩擦力矩为上下球铰面每个微面积上的摩擦力矩之和(见图1)。

图1 转动体球铰静摩擦系数计算示意图

球铰的静摩擦力矩dMZ=RcosθdF，dF=μ0σdA，dA=2πrds，r=Rsinθ，σ=σ竖cosθ,σ竖=N（/πR2sin2α），则

将球铰参数代入得：α=14.479°，球铰静摩阻系数μ0=MZ/（0.985NR），摩擦面按平面计算时，球铰静摩阻系数μ0=MZ/（NR）。计算结果两者相差1.5%，因此若球铰的球面半径较大而矢高比较小时，可将球铰摩擦面简化为平面来计算摩阻系数。

2.2 测点布置及测量参数

桥梁正式转体前，应进行试转，试转严格控制在铁路限界边以外。试转前，需进行称重平衡试验，测试转体部分的不平衡力矩、偏心矩、摩阻力矩及摩擦系数等参数，实现桥梁转体的配重要求。在上转盘下用千斤顶施加力，分别用位移计测出球铰由静摩擦状态到动摩擦状态的临界值，上转盘两侧的力差即为不平衡重量。

根据该状态的测试方法，在两幅梁的承台底面布置4台400 t的千斤顶，纵向距球铰中心为4.09 m，横向距球铰中心为3.06 m。在上转盘边缘布置4个百分表测量转体墩的竖向位移。具体布置如图2和图3所示。

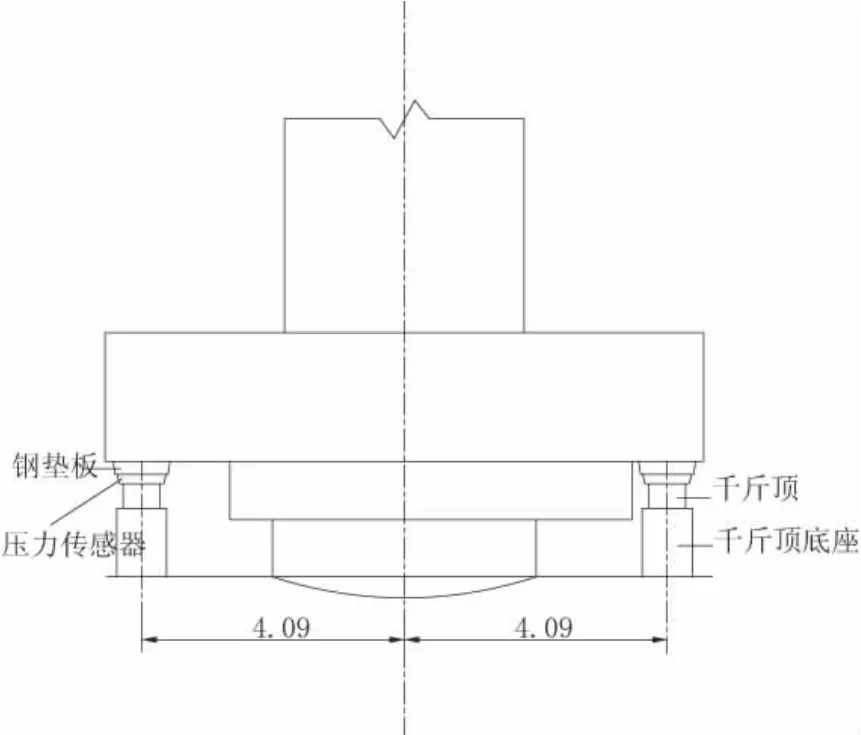
图2 千斤顶布置立面图（单位：m）

图3 千斤顶布置平面图

2.3 试验步骤

转体梁称重步骤如下：

（1）在所选断面处布置位移传感器和顶升千斤顶；

（2）千斤顶同步逐级加力，记录位移传感器的微小位移，直到位移出现突变，为保证数据的可靠性，每侧顶升两次，并校核记录的数据；

（3）绘制出转体梁P-Δ曲线；

（4）重复以上试验；

（5）对转体梁纵向和横向分别进行顶升试验；

（6）确定梁体不平衡力矩、偏心距、球铰摩阻系数；

（7）确定梁体的配重量、位置。

3 称重结果分析

梁体脱架后，分别对18#墩和19#墩的撑脚进行观察，两桥墩撑脚与滑道之间的间距均只发生微小的变化，可以判断两转体墩的不平衡模式属于第二种情形，即转体墩球铰摩擦力的力矩大于梁体不平衡力矩，撑脚没有受力，摩擦力矩与梁体的不平衡力矩维持了整个转体梁的稳定。

3.1 18#墩试验结果

18#墩实测位移和顶力的关系曲线如图4～图7所示，千斤顶在上转盘上的作用点距离球铰中心点纵向的等效力臂为L1=L2=4.09 m，横向等效力臂为L3=L4=3.06 m。

图4 18#墩纵向小里程侧顶力-位移曲线

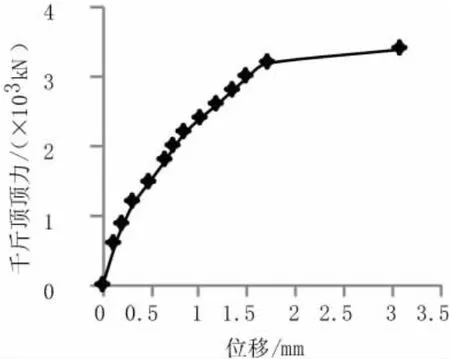
图5 18#墩纵向大里程侧顶力-位移曲线

图6 18#墩横向左侧顶力-位移曲线

图7 18#墩横向右侧顶力-位移曲线

由图可知，梁体发生刚体位移突变，小里程侧顶升力为2 000 kN，大里程侧顶升力为3 200 kN，横向左侧顶升力为3 200 kN，右侧顶升力为34 000 kN。根据相关公式可得出18#墩纵向不平衡力矩MG= 2 454 kN·m；球铰纵向摩阻力矩MZ=10 634 kN·m；纵向偏心距е=0.082 m，纵向滑动时球铰静摩阻系数μ0=0.060；横向不平衡力矩MG=306 kN·m；铰纵向摩阻力矩MZ=10 098 kN·m；纵向偏心距е=0.010 m，纵向滑动时球铰静摩阻系数μ0=0.057。

3.2 19#墩试验结果

19#墩实测位移和顶力的关系曲线如图8～图11所示，千斤顶在上转盘上的作用点距离球铰中心点纵向的等效力臂为L1=L2=4.09 m，横向等效力臂L3=L4=3.06 m。

图8 19#墩纵向小里程侧顶力-位移曲线

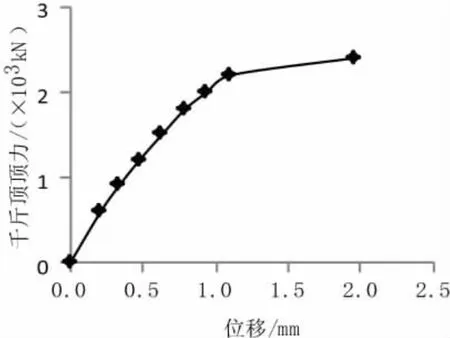
图9 19#墩纵向大里程侧顶力-位移曲线

图10 18#墩横向左侧顶力-位移曲线

图11 18#墩横向右侧顶力-位移曲线

由图可知，梁体发生刚体位移突变，小里程侧顶升力为3 200 kN，大里程侧顶升力为2 200 kN，横向左侧顶升力为3 400 kN，右侧顶升力为36 000 kN。根据相关公式可得出18#墩纵向不平衡力矩MG= 2 045 kN·m；球铰纵向摩阻力矩MZ=11 043 kN·m；纵向偏心距е=0.051 m，纵向滑动时球铰静摩阻系数μ0=0.062；横向不平衡力矩MG=306 kN·m；铰纵向摩阻力矩MZ=10 710 kN·m；纵向偏心距е=0.010 m，纵向滑动时球铰静摩阻系数μ0=0.060。

3.3 配重

转体墩在脱架后在不平衡力矩和球铰的摩擦力矩的作用下处于自平衡状态，梁体的不平衡力矩较小，采用质量平衡转体配重，此种配重方法操作简单方便，所需配重较小，由于转体墩的整个质量都由球铰承担，撑脚和滑道之间分离开，有效地减小了转体过程中的摩擦阻力，减小了转体所需的牵引力。通过对18#墩、19#墩称重结果分析可知，18#墩转动体不平衡力矩偏向大里程侧，需要在大里程侧进行配重，19#墩转动体不平衡力矩偏向小里程侧，需要在小里程进行配重。配重量的计算可根据以下公式确定：

所需配重（G）=不平衡力矩（MG）/配重力臂（L）

为了尽量减小梁体的配重同时保证安全，梁体上的配重布置在距离梁端2 m的位置，则配重力臂L=28 m。

18#墩小里程配重重量为G=2 454/28.0=87.6 kN，布置在小里程侧距梁端2 m处。

19#墩大里程配重重量为G=2 045/28.0=73 kN，布置在大里程侧距梁端2 m处。

18#墩、19#墩横向不平衡力矩均很小，可以不进行配重。