Matlab在离散点拟合椭圆及极值距离计算中的应用

吴美容，王建国

(南京太亚科技有限责任公司，江苏 南京 210061)

Matlab在离散点拟合椭圆及极值距离计算中的应用

吴美容，王建国

(南京太亚科技有限责任公司，江苏 南京 210061)

目前关于根据离散点建立椭圆的一般二次曲线方程，并由此推导椭圆的标准方程以及计算离散点距离椭圆极值方面的文献较少，文章重点介绍了利用Matlab软件进行公式推导的详细过程以及计算极值的方法。极值计算方法介绍了几何作图法、迭代计算法、穷举法、人工智能算法。实例验证表明了思路与算法的正确性和实用性，可以为解决其他二次曲线和二次曲面的问题提供借鉴。

椭圆；拟合；距离极值；算法；人工智能；最优化

0 引言

椭圆、双曲线、抛物线等都是平面二次曲线，本文针对椭圆进行讨论。张元元将椭圆拟合应用在工程隧道形体检测[1]，闫蓓将椭圆拟合应用在医学瞳孔中心定位系统[2]，应该说现实世界中椭圆形状的物体较多，经常会碰到需要确定这些椭圆实体的几何参数(中心、长短半轴、旋转角度)，通过采集椭圆上一系列离散点进行椭圆拟合是较为常用的处理方法。目前较多的文献都是直接给出公式，侧重于椭圆拟合的应用，却没有给出数据处理的整体思路以及公式推导的方法，读者不清楚公式是如何得出的，有的公式甚至还是错误的，直接套用会发现结果不正确，如文献[2]公式(4)、(5)。本文着重介绍Matlab在椭圆拟合数据处理中的具体应用。此外，目前讨论离散点距拟合椭圆极值距离的文献较少，本文也在这方面进行了探讨。

1 椭圆方程的建立

椭圆的一般二次曲线方程可表示为：

F(X，Y)=AX2+BXY+CY2+DX+EY+F=0

(1)

式(1)有6个未知参数，其中，F为常数项，因此，至少需要5个以上的点来确定椭圆的二次曲线方程。为了数据处理的方便，一般需要对原始数据X、Y进行正规化处理，代码描述：

mx = mean(X)；

my = mean(Y)；

sx =(max(X)-min(X))/2；

sy =(max(Y)-min(Y))/2；

x =(X-mx)/sx；

y =(Y-my)/sy；

正规化数据对应的二次曲线方程记为：

f(x，y)=ax2+bxy+cy2+dx+ey+f=0

(2)

对于计算式(2)中的6个参数，可以调用Matlab自带的regress()，该函数为基于最小二乘原理多元线性回归，构造矩阵：

输入命令：regress(Y，X)即可算出系数。该步骤也可以输入如下命令：inv(X′*X)*X′*Y。实际计算时可取f=1。通过以上步骤，6个参数abcdef都已经计算出来了，为已知值。现在要反归一化，通过abcdef反算ABCDEF。推导过程借助Matlab符号运算，代码描述：

syms x y X Y mx my sx sy a b c d e f；

x =(X-mx)/sx；

y =(Y-my)/sy；

f=a*x^2+b*x*y+c*y^2+d*x+e*y+f；

pretty(f)

结果：

分别将X^2，XY，Y^2，X，Y系数提取出来，可以辅助用collect()命令简化提取工作。

通过以上步骤，ABCDEF已经计算出来了，为已知值。截至目前，椭圆的二次曲线方程已知。下面推导如何转换为几何标准形式方程，进而计算出5个参数。

首先假设式(1)中的各系数已知。现在把坐标轴逆时针转动θ角度，其中(x′，y′)表示点(x，y)在坐标轴变动后的新坐标：

(3)

把式(3)代入式(1)，设新方程为：

a′x′2+b′x′y′+c′y′2+d′x′+e′y′+f′=0

(4)

容易求出：

a′=Acos2θ+Bcosθsinθ+Csin2θ

b′=(C-A)sin2θ+Bcos2θ

c′=Asin2θ+Bcosθsinθ+Ccos2θ

d′=Dcosθ+Esinθ

e′=-Dsinθ+Ecosθ

f′=F

为了使坐标轴变换后，方程不再出现x′y′一项，即b′=0，则有：

(5)

为了让x′y′项的系数为0，需令

(6)

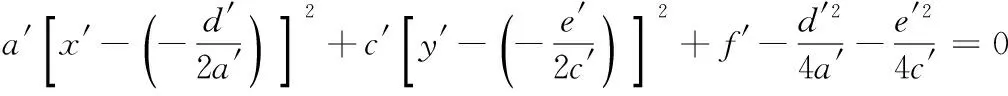
(7)

则有：

(8)

此时的U和V即椭圆的两半轴长，再利用式(3)将目前的椭圆中心点坐标(x0′，y0′)转变为坐标轴变换之前的(x0，y0)。以上符号公式的推导仍然借助于Matlab符号运算。

于是，从椭圆一般方程的系数得到了椭圆的两半轴长、中心坐标以及U半轴关于X坐标轴的角度(逆时针为正向)。

2 离散点距拟合椭圆极值距离计算

方法1(几何作图法)：

离散点到曲线最小距离，采用文献[3]里面的第1种思路也是可以的，但是手工计算存在效率较低的问题，可作为一种辅助计算手段。

方法2(解非线性方程组法)：

文献[3]里面的第2种思路也可以，k1×k2=-1，根据该思路可建立如下2个方程：

(9)

Ax02+Bx0y0+Cy02+Dx0+Ey0+F=0

(10)

具体如下：

将式(9)、式(10)联立计算离散点(px，py)对应于拟合椭圆上的最近点(x0，y0)，反算得到距离极值。求解上面的方程组得出关于x0、y0的解析式较麻烦，考虑迭代算法。直接利用fsolve()函数，以点(112.6614，-165.52)为例。首先建立M文件：

function f=myfun(x)

A=4.89939E-05；B=5.62288E-08；

C=0.000115288；D=-0.008437616；

E=0.016865307；F=-0.031413295；

px=112.6614；py=-165.52；

f1=(-(2*A*x(1)+B*x(2)+D)/(B*x(1)+2*C*x(2)+E)*(py-x(2))/(px-x(1)))+1；

f2=(A*x(1)^2+B*x(1)*x(2)+C*x(2)^2+D*x(1)+E*x(2)+F)；

f=[f1 f2]；

end

然后输入如下代码：

fsolve(@myfun，[112 -165]，optimset(‘MaxFunEvals’，100，‘MaxIter’，100))%最小距离对应的椭圆点

结果如下：

ans =112.6287 -165.2517

输入如下代码：

fsolve(@myfun，[14 -26]，optimset(‘MaxFunEvals’，100，‘MaxIter’，100))%最大距离对应的椭圆点

结果如下：

ans =-35.8312 -23.6046

采用该方法能很好计算出正确的结果，坐标反算最小最大距离分别为：0.270 3，205.402 1。针对该函数计算时较依赖初值，容易陷入局部极小，采取如下对策：计算最短距离时，初值可直接取离散点数值的整数部分或所在象限中以椭圆长短半轴为两边所构成的长方形区域(近似)中心点的数值；计算最大距离时，初值可取对角象限中以椭圆长短半轴为两边所构成的长方形区域(近似)中心点的数值。

方法3(传统最优化算法)：

>>syms t；px′=26.5498；py′=-92.3433；

x=143.7082651857737*cos(t)；y=93.6831595721793*sin(t)；

f=sqrt((x-px′).^2+(y-py′).^2)；

>> [x，minf]=minNewton(f，0)

计算结果：

x =2.5848

minf =205.4007

>> [x，minf]=minPWX(f，0，4)

计算结果：

x =4.8980

minf =0.2707

以上分别用基本牛顿法和抛物线法计算了极大值和极小值。该方法较实用，如调用Matlab自带的函数fminsearch()、fminunc()也可以。

方法4(人工智能算法)：

群智能算法SIA，本文以粒子群算法和鱼群算法为例进行介绍，经笔者测试其他智能算法，如遗传算法ga()、模拟退火算法saa()等也都能在很短的时间内获得准确的结果。

粒子群算法：

首先建立目标函数文件myfunpso()：

function f=myfunpso(t)

px1=26.5498；py1=-92.3433；

x=143.7082651857737*cos(t)；

y=93.6831595721793*sin(t)；

f=sqrt((x-px1).^2+(y-py1).^2)；

end

命令窗口输入：

>> [xm，fv]=PSO(@myfunpso，40，2，2，0.5，100，1)

结果如下：

xm =-1.385213897691377 fv =0.270784374867295

计算最大值，将目标函数文件改为：f=-sqrt((x-px1).^2+(y-py1).^2)；

输入命令后，结果如下：

xm =2.584791470317521 fv =-2.054007419382480e+002

鱼群算法迭代过程如图1所示。

图1 鱼群算法迭代过程Fig.1 Iterative process of fish-swarm algorithm

对比上面方法3用传统的最优化算法，结果是一致的。群智能算法属于随机算法，不要求函数连续、可导，应用时需要设置恰当的参数，多次运行程序以提高可靠性。

方法5(遍历法)：

本文再介绍一种经典的遍历算法来计算极值。思路：第一，将离散点坐标转换到标准椭圆坐标系；第二，判断离散点位于哪个象限；第三，离散点与属于该象限椭圆上的点按步长计算距离并比较取最小值，此外，一、二象限，离散点y值大于椭圆点y值，距离取正，否则取负；三、四象限，离散点y值小于椭圆点y值，距离取正，否则取负；第四，离散点与所属象限的对角象限上的椭圆点按步长计算距离并比较取最大值。算法流程图如图2所示。

图2 算法流程图Fig.2 Algorithm flow chart

程序采用的思路，根据点位落在的象限区间，缩小搜索范围，不需要每个点都要全区域搜索，提高了运行的效率。

3 具体应用

测试用例采用文献[4]，具体数据如表1所示，程序截图如图3、图4、图5所示。

表1 离散点数据

图3 读取数据文件Fig.3 To read the data files

图4 计算结果Fig.4 Calculation results

图5 离散点与拟合椭圆Fig.5 Discrete points and fitting ellipse

4 结论

通过应用分析，笔者可得到如下结论：

1)程序只需读取原始测量数据TXT文件即可自动输出拟合椭圆及离散点分布图，直观明了；能够自动输出椭圆5个参数以及每个离散点对应于拟合椭圆的最大距离与最短距离；文献[4]椭圆中心坐标值86.105 7错误，应该改为86.150 7，最小值输出结果与文献[4]结果相差2 mm内。程序结果正确，操作简单，自动化程度高。

2)程序椭圆拟合算法基于最小二乘原理，最小二乘原理本身不具备较强的抗差能力，若加上稳健估计或粗差剔除功能模块，将更加提高程序的自动化程度。

3)无论平面坐标转换还是空间三维坐标转换都是工程测量和工业测量数据处理过程中最基础也是必要的步骤。

4)文章介绍了5种计算离散点到拟合椭圆极值距离的数据处理方法，实践中综合运用以上5种方法可以取得很好的计算效果。计算极值问题，若采用人工智能算法，如：模拟退火算法等，具有很好全局最优解的搜索能力，属于随机算法，对初值也不敏感，若设置好冷却进度表相关参数，计算效果会很好；若采用传统算法，为避免陷入局部极小，采用作图法作大致判断也是很有必要。各种算法的优势互补，算法集成是很有意义的研究方向。例如，将模拟退火算法、遗传算法、粒子群算法与文献[5]的BP神经网络算法进行融合，优化神经网络连接权值和阈值。

5)程序的思路可以为点到一般二次曲线(如：双曲线，抛物线等)及点到一般二次曲面的极值计算问题提供借鉴。

6)文献[6]较详细的介绍了溢流堰表面形体检测工作中涉及的检测点距离直线、多圆心圆弧、抛物线、缓和曲线等线元最小值的计算方法，实际上溢流堰图纸也经常设计有四分之一椭圆，本文针对点距离该线元极值的计算提出了比较实用的解决思路。

[1] 张元元，杨国东，王凤艳.丹麦法稳健估计在隧道椭圆拟合中的应用[J].世界地质，2012，31(1)：199-203.

[2] 闫蓓，王斌，李媛.基于最小二乘法的椭圆拟合改进算法[J].北京航空航天大学学报，2008，34(3)：295-298.

[3] 王建国.迭代计算方法在测绘领域中的具体应用[J].城市勘测，2011(2)：153-154

[4] 王解先，季凯敏.工业测量拟合[M].北京：测绘出版社，2008：57-61.

[5] 王建国，吴美容.运用BP人工神经网络设计变形预报模型[J].矿山测量，2010(4)：73-75.

[6] 吴美容，王建国.溢流堰表面形体检测研究[J].现代测绘，2016，39(2)：54-56.

Application of Matlab in Fitting Ellipse and Calculating Extremum Distance of Discrete Points to Ellipse

WU Mei-rong，WANG Jian-guo

(NanjingPaciaTechnology&ScienceCo.,Ltd.，NanjingJiangsu210061，China)

According to the fact that there is no enough documents about establishing general quadratic curve equation based on discrete points，deducing standard geometric symbolic equation，and calculating the extremum distance with the use of mathematical computer language(Matlab).This article focuses on the detailed process of formula derivation and the method of calculating the extreme value with Matlab.The article presents the following methods：geometric drawing method，iterative method，exhaustive method，and AI algorithm.The practical example verifies the correctness and practicability of the method and the algorithm，which can be used for reference to solve the problems of other conic curves and quadric surfaces.

ellipse；fitting；distance extremum；algorithm；artificial intelligence；optimization

2016-07-05

TP 301.6

：A

：1007-9394(2016)04-0020-04

吴美容(1982～)，女，江苏海安人，学士，工程师，现主要从事地理信息系统数据处理及项目管理方面的工作。