基于DEM的地形起伏度最佳计算尺度的研究
——以仙居县为例
2017-01-05范鹏宇朱校娟郭啸川
范鹏宇,朱校娟,郭啸川
(1.浙江省测绘大队,浙江 杭州 310000; 2.浙江省地理信息中心,浙江 杭州 310000)
基于DEM的地形起伏度最佳计算尺度的研究
——以仙居县为例
范鹏宇1,朱校娟2,郭啸川2
(1.浙江省测绘大队,浙江 杭州 310000; 2.浙江省地理信息中心,浙江 杭州 310000)
在区域性研究中,地形起伏度是反映地形起伏特征的宏观因子,利用 DEM 数据作为基本信息源,能够快速、直观地提取地形起伏度。本文以仙居县1∶1万 DEM数据作为基础数据源,利用矩形窗口的邻域分析获取多尺度地形起伏度,探讨提取适合研究区地貌分类的地形起伏度最佳统计单元,并统计不同地貌类型面积比。研究表明,仅仅依靠地形起伏度一个指标作为划分地貌形态的指标,有一定的局限性。本文加入海拔高度作为辅助因子后,更有效地划分了平原与丘陵地貌,分类结果更加准确。
DEM;地形起伏度;尺度;最佳统计单元;海拔高度
0 引言
地形起伏度指在一个特定区域内高程最大与最小值之差,是反映一个区域地形起伏特征的宏观指标,也是定量描述和划分地貌形态的重要指标[1]。郎玲玲等以福建低山丘陵地区多尺度DEM为数据,提取多尺度DEM地形起伏度进行比较,最终得出1∶25万DEM的最佳统计单元为4.41 km2,1∶10万DEM的最佳统计单元为0.4 km2[2]。唐飞等选取了代表新疆基本地貌特征的准噶尔盆地及其西北山区为研究区,进行地形起伏度的研究,得出利用1∶25万DEM的地形起伏度的最佳统计单元面积为4 km2[3]。随着空间信息技术的广泛应用,利用DEM数据作为基本信息源,能够快速、直观地提取地形起伏度。前人的研究表明,不同区域、不同尺度的DEM存在不同的地形起伏度最佳统计单元[4-7]。确定最佳统计单元,推动不同地貌类型的分类指标从定性走向定量。
1 实验研究基础
1.1 实验样区
本文以浙江省仙居县作为实验样区,其实验样区的DEM数据如图1所示。仙居县位于E120°17′6″~120°55′51″,N28°28′14″~28°59′48″之间,县域面积约为2 000 km2,其中以丘陵山地为主,地形从外向内倾斜,略向东倾,各支脉斜交层叠,构成多级梯状平台,平台上缓丘起伏,围成大小不等、错落相间的谷地和盆地。

图1 实验样区DEM数据Fig.1 DEM of test region
1.2 实验数据
本研究依托实验样区1∶1万DEM数据为基础,分辨率为5 m×5 m,最小高程为13.5 m,最大高程为1 380.9 m,平均高程为494.1 m。
1.3 理论基础
根据地形地貌的基本理论以及前人的研究总结出如下理论:对于相同的DEM,随着像元统计单元由小到大,存在一个使最大高差达到相对稳定的最佳统计单元,且单元内最大值与最小值的相对高差,无论何处总是从小变大,直到像元统计单元达到某一阈值后,这种高差基本稳定在一个数值上,这一阈值所对应的统计单元为最佳统计单元,所对应的高差值为起伏高度[5-6]。
本研究基于以上理论基础,运用GIS技术作为研究方法,以仙居县1∶1万DEM数据为基础数据源,进行多尺度地形起伏度的计算,提取适合研究区的最佳统计单元。
2 地形起伏度计算
2.1 邻域分析
邻域工具是基于自身位置值以及指定邻域内识别的值为每个像元位置创建输出值。邻域分析(Neighborhood Analysis)是一种窗口分析,按分析窗口的特征可划分为矩形、圆形、环形、楔形、不定期和权重6种基本类型,其统计类型包括最大值、最小值、平均值、范围、标准差、众数、少数、总和统计、中值和变异度统计10种统计类型。本次研究运用ArcGIS软件中邻域分析工具中的焦点统计(Focal Statistics),分别计算其最大值和最小值,再将最大值和最小值做差值运算。
2.2 基于矩形邻域类的多尺度地形起伏度计算
本研究根据以上的分析,将邻域设定为长宽相等的矩形(NbrRectangle),设置5×5为初始邻域,以5为步长,将500×500设定为最终邻域,计算出整幅DEM在各矩形分析窗口内高程最大与最小值之差,得到每个分析窗口下的地形起伏度,以每个分析窗口地形起伏度的均值作为其参考值,展开多尺度地形起伏度计算。在EXCEL中对起伏度做拟合对数曲线,如图2所示。
拟合对数方程为:
y= 146.14ln(x)-176.36
(1)
决定系数R2=0.936 9,拟合度良好。

图2 按邻域大小提取的地形起伏度统计图Fig.2 Statistical chart of relief amplitude by neighborhood size
结合研究区域地形地貌特征,参照中华人民共和国1∶100万地形地貌制图划分规范,将地形起伏度按表1分为5种类型,地貌基本形态划分指标如表1所示。

表1 地貌基本形态划分指标
利用ArcGIS软件的重分类(Reclassify)工具批量对各尺度地形起伏度按此划分标准进行分类,并统计各尺度下每种类型的面积,得到各种类型地形起伏度所占面积百分比变化曲线图,如图3所示。
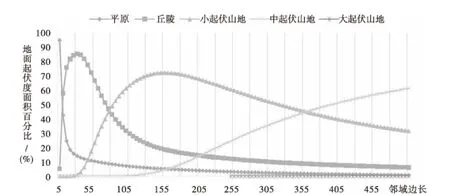
图3 不同类型地形起伏度面积百分比随尺度变化图Fig.3 Percentages of various types of relief amplitude area with increasing scales
从图2可以看出,起伏度曲线随邻域边长增大呈现上升的趋势,且随着边长递增,上升速度越慢。
从图3可以看出,每个地貌类型所占地形起伏度的面积比例随邻域边长变化各有不同。其中,平原所占面积比例随邻域边长增大呈递减趋势,这也是唯一一个随邻域边长增大面积比例递减的地貌类型;丘陵所占面积比例随邻域边长增大呈先增后减的态势;对于小起伏山地,所占面积比例随邻域边长增大也呈现先增后减的态势,但其增减的区域与丘陵不一致;对于中起伏山地,领域边长小于105×105时所占面积比例极少,随后随着邻域边长的增大面积比呈明显上升趋势;对于大起伏山地,起初面积所占比例为0,当邻域边长达到250×250后才出现。
实验表明,传统的地形地貌类型的划分具有一定的尺度依赖性,因此需要确定一个最适宜尺度地形起伏度来进行地貌形态的划分。
2.3 确定地形起伏度的最佳尺度
按照区域普适性和山体整体性两个原则[4],利用高差显著性变化模型[7],得到基于矩形邻域获得的多尺度地形起伏拐点判断公式如下:
(2)
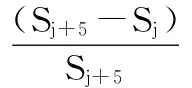
针对矩形邻域所计算的多尺度地形起伏度,依据式(2)展开计算,得到Ij随尺度变化图(图4)。

图4 变化强度Ij随尺度变化图Fig.4 Change intensity with increasing scale
通过图4可以看出,矩形邻域对应的最佳尺度为270×270,面积约为1.8 km2。表2为最佳尺度下各种地貌类型所占面积。
表2 最佳尺度下各种地貌类型面积比重表
Tab.2 Percentages of various types of geomorphological area with optimal scale

最佳尺度≤30m30~200m200~500m500~1000m>1000m溪滩水域总计270×2702.66%10.28%52.60%26.45%0.01%8%100%
实验结果表明,确定的最佳尺度下的地形起伏度能有效地区分了大、中、小起伏山地,山地与平原区分明显,但与地表实际状况仍有部分差异,存在一定的局限性,其原因有以下2点:
1)大量实验证明,由于大比例尺、高分辨率DEM数据本身含有大量微观地形信息,以这样的DEM数据作为基础数据源提取反映宏观特征的地形起伏度,并且仅仅利用邻域边长递增的方法很难达到理想的效果。
2)由于DEM数据只反映微观的局部相对高度,而地形起伏度是反映地形起伏特征的宏观指标,因此还要考虑宏观的海拔高度。因为海拔高度既是制约外营力的作用方式,又能作为客观的基准尺度。这样人们在观察相对高度的地形起伏的同时,又重视了绝对高度的客观作用。
因此不能按照统一的指标来划分地貌类型[8]。为更准确的区分研究区中平原和丘陵地貌类型,本文增加了海拔高度这个辅助因子。
在30~100 m之间,10 m为步长进行试验,确定海拔高度的阈值,试验表明,当辅助因子海拔高度选取50 m时,其得到的结果与地表的实际状况最为吻合。将海拔高度小于50 m作为平原的补充约束条件后,与之前分类结果比较(如图 5),平原的百分比增加了3%,相应丘陵和山地共减少3%。
研究表明,对地貌形态进行划分时,加入海拔高度因子后得到的分类结果,比仅仅使用地形起伏度能更有效地区分相似的地貌类型。
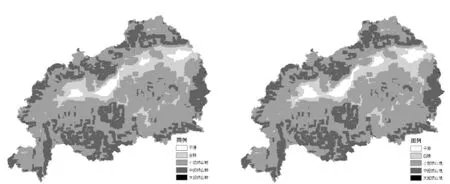
图5 加入海拔高度前后地貌分类对比图Fig.5 Comparison charts of geomorphological classification before and after adding altitude factor
3 结论
本研究以仙居县1∶1万DEM数据为实验数据,利用ArcGIS软件的邻域分析模块获取多尺度地形起伏度,分析不同尺度下地貌分类的结果,确定地形起伏度最佳统计单元,并加入海拔高度辅助因子进行对比研究。得到以下结论:
1)以山地丘陵为主的仙居县在1∶1万DEM下计算地形起伏度的最佳统计单元为1.8 km2。
2)地形起伏度存在明显尺度依赖特征和一定的局限性,大比例尺、高分辨率DEM数据本身含有大量微观地形信息的特性,因此需要结合研究区地形特点,筛选多个地形信息因子来进行地貌形态的划分,能够获得更好的地貌分类结果。
3)将海拔高度小于50 m作为平原的补充约束条件后,对平原和丘陵地貌类型划分更准确,分类结果更理想。
[1] 朱红春,陈楠,刘海英,等.自1∶10 000比例尺DEM提取地形起伏度——以陕北黄土高原的实验为例[J].测绘科学,2005,30(4):86-88.
[2] 郎玲玲,程维明,朱启疆,等.多尺度DEM提取地势起伏度的对比分析——以福建低山丘陵区为例[J].地球信息科学,2007,9(6):1-6.
[3] 唐飞,陈曦,程维明,等.基于DEM的准噶尔盆地及其西北山区地势起伏度研究[J].干旱区地理,2006,29(3):388-392.
[4] 邵崇建,李勇,颜照坤,等.基于DEM数据的龙门山流域地形起伏度研究[J].四川师范大学学报:自然科学版,2015,38(5):766-773.
[5] 徐汉明,刘振东.中国地势起伏度研究[J].测绘学报,1991,20(4):311-319.
[6] 徐汉明,刘振东.中国地势起伏度最佳统计单元的求证[J].湖北大学学报:自然科学版,1990,12(3):266-271.
[7] 张磊.基于地形起伏度的地貌形态划分研究——以京津冀地区为例[D].石家庄:河北师范大学,2009.
[8] 蒋国富.基于SRTM DEM与ArcGIS的南阳市地貌形态类型的自动划分[J].南阳师范学院学报,2015,14(12):43-46.
Study on Optimal Scale for Calculating Relief Amplitude Based on DEM:A Case of Xianju County
FAN Peng-yu1,ZHU Xiao-juan2,GUO Xiao-chuan2
(1.SurveyingandMappingBrigadeofZhejiang,HangzhouZhejiang310000,China; 2.GeomaticsCenterofZhejiang,HangzhouZhejiang310000,China)
In the regional studies,relief amplitude is a macroscopic factor that reflects the topographic relief,and using DEM data to extract relief can quickly and intuitively reflect topographic relief feature.In this paper,based on the 1∶10 000 DEM data in Xianju county,the author used neighborhood analysis of rectangular analysis window to obtain multi-scale relief,and determined optimal statistical unit of suitable for the study area of geomorphologic classification,and counted the area ratio of various geomorphic type.The research shows that it just rely on relief as an indicator of geomorphologic forms classification index have certain limitations.In this paper,after added the altitude as the auxiliary factor,the plain and hilly terrain are divided more effectively,and the classification results are more accurate.
DEM;relief amplitude;scale;optimal statistical unit;altitude
2016-07-23
P 931
:B
:1007-9394(2016)04-0036-03
范鹏宇(1988~),女,山西岚县人,硕士,工程师,现主要从事基础测绘方面的工作。
