基于MEMsFEM的功能梯度压电板力电耦合分析*

孟广伟 李霄琳 周立明† 李锋 王晖

(1.吉林大学 机械科学与工程学院, 吉林 长春 130022； 2.吉林大学 建设工程学院, 吉林 长春 130026)

基于MEMsFEM的功能梯度压电板力电耦合分析*

孟广伟1李霄琳2周立明1†李锋1王晖1

(1.吉林大学 机械科学与工程学院, 吉林 长春 130022； 2.吉林大学 建设工程学院, 吉林 长春 130026)

功能梯度压电材料(FGPM)是一类材料特性连续变化的力电耦合材料.由于材料性能的不均匀性,相应的力学分析具有很大挑战.基于混合扩展多尺度有限元法(MEMsFEM)建立了FGPM力电耦合问题的分析模型.采用传统多尺度有限元法构造电势多尺度基函数,用扩展多尺度有限元法在不同坐标方向构造位移多尺度基函数,并通过引入耦合附加项考虑各坐标方向位移场间的耦合作用.多尺度基函数的构造可以有效捕捉材料的非均质性,由此可以在粗尺度上对问题进行求解,明显减少了计算量.最后通过数值算例验证了MEMsFEM的有效性和高效性.文中模型为功能梯度材料力学行为的数值模拟提供了有效途径.

混合扩展多尺度有限元;功能梯度材料;压电材料;力电耦合

压电材料是一类典型的力电耦合材料,通过响应机械应力产生电势,通过响应外加电压产生应力应变.压电元件通常由一层压电材料制成,存在变形小、承载能力低等问题.为提高性能,常常将其制备为多层结构.但由于不同材料结合处的物性参数变化不连续，层间粘结处会产生很大应力,易形成裂纹,导致使用寿命缩短.为了解决此问题,Wu等[1- 3]将功能梯度材料的理念引入到压电结构中,提出了功能梯度压电材料(FGPM).

功能梯度材料[4- 6]是一种通过连续改变各组分含量使材料的宏观力学特性在空间上呈连续梯度变化的非均质复合材料.由于功能梯度材料性能的不均匀性,使得针对均匀材料所提出的力学理论和计算方案不再适用于功能梯度材料.比如普遍使用的有限元法,其需要单元内部材料属性必须为均质的,因此要求离散的网格尺寸小于非均质材料的特征尺寸才可以得到精确的结果,从而导致自由度过大,求解困难.因此，建立一种针对功能梯度材料的高效可行的数值算法是十分必要的.

多尺度有限元法[7- 9]是近几年发展起来的用于求解非均质标量问题的有效方法.该算法通过构造数值多尺度基函数捕捉材料的微观非均质信息,由此可以在宏观尺度上对问题进行求解.扩展多尺度有限元法是在多尺度有限元法基础上提出的求解非均质固体力学矢量问题的数值算法.该算法在构造多尺度基函数时引入耦合附加项,由此考虑固体变形的泊松效应,提高了计算精度.扩展多尺度有限元法已被成功应用于非均质材料的弹塑性问题[10]、热弹性耦合问题[11]、拓扑优化[12]以及屈曲分析[13]中,并获得了良好效果.

文中基于混合扩展多尺度有限元法建立了功能梯度压电材料力电耦合问题的分析模型,通过构造可以有效反映粗网格单元内非均质特性的位移多尺度基函数和电势多尺度基函数将结构的微观信息映射到宏观尺度上,并通过数值算例对算法的有效性进行了验证.

1 FGPM力电耦合问题的控制方程

基于FGPM的基本方程得到的力电耦合问题的控制方程如下：

(1)

在边界上满足如下条件：

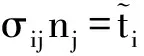
(2)

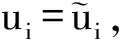
(3)

(4)

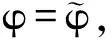
(5)

针对功能梯度压电材料板,设其材料参数沿厚度方向(x3方向)按同一函数规律连续变化:

(6)

(7)

(8)

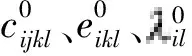
指数函数分布:

f(x3)=eα(x3/h)

(9)

幂函数分布:

(10)

正弦函数分布:

(11)

式中，α、β、γ为形状因子,h为板厚.

2 混合扩展多尺度有限元基本原理

多尺度有限元法同传统有限元法的本质区别在于传统有限元法的基函数是给定的解析表达式,与材料特性无关,而多尺度有限元法的基函数通过局部求解单元平衡方程构造,因此这些基函数可以反映单元内部材料的非均质性,使问题在粗尺度上求解就可以得到满意的结果.

2.1 电势多尺度基函数的构造

由于力电耦合问题存在位移和电势两个基本变量,需要分别构造其多尺度基函数[11].电势为标量,基函数可以采用传统多尺度有限元法求解.设研究区域为长方体a×b×h,将其剖分为一定数目的粗网格和细网格单元.其中细网格单元要求解析材料的非均质性,在细网格上计算的有限元结果要求达到问题需要的求解精度;对于粗网格单元,其划分一般没有特殊的限制,粗网格内的材料属性可以是非均质的,如图1所示.

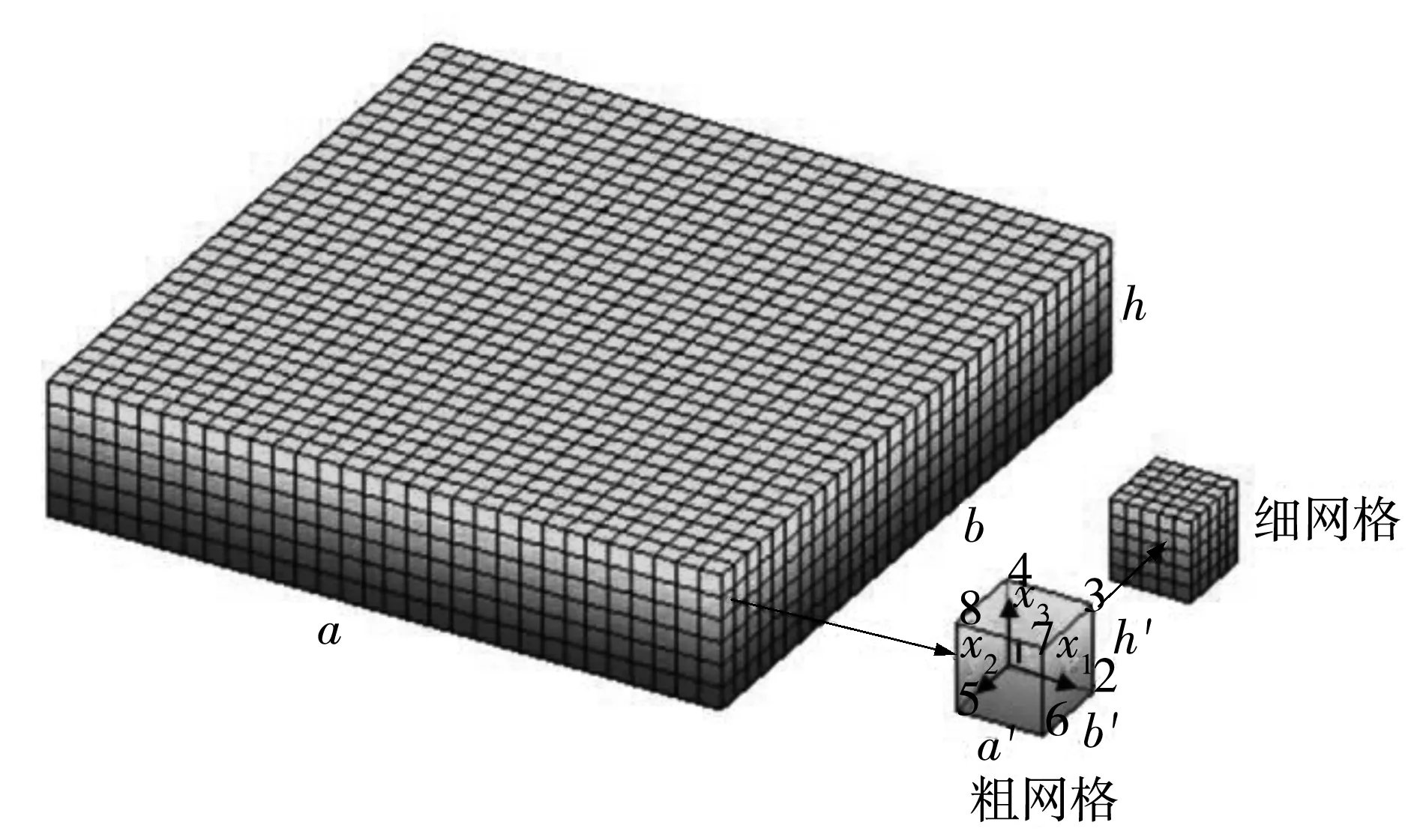
图1 粗网格和细网格的剖分

粗网格内细网格任意节点的电势可表示为

(12)

(13)

(14)

(15)

(16)

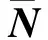
(17)

(18)

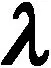
2.2 位移多尺度基函数的构造

位移场为矢量场,需要在各坐标方向分别构造基函数.根据扩展多尺度有限元基本原理,考虑固体变形时各坐标方向位移场间的耦合作用引入耦合附加项,则粗网格内细网格任意节点的位移可表示为

(19)

(20)

(21)

(22)

(23)

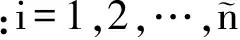
位移多尺度基函数满足:

(24)

2.3 宏观矩阵的组装

多尺度基函数构造完成后即可以推导粗网格单元的宏观矩阵,利用式(12)和(19),由Green公式及Galerkin法推得力电耦合问题的多尺度有限元列式为

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

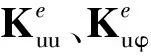
(39)

(40)

(41)

由式(25)可以得到粗网格单元的位移和电势,由式(39)可以获得细网格单元的位移和电势值,进而根据几何方程和物理方程获得单元的应力和应变.

3 数值算例

以四边简支、接地的功能梯度压电板(a=b=1 m,h=0.1 m)作为研究对象,设其材料属性沿板厚方向按指数分布,取α=-0.5,板的底部材料取为PZT-4,其材料参数分别为:

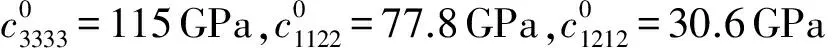
考虑以下两种加载形式.

工况1:

(42)

工况2:

(43)

式中，上标+表示板的上表面.

依据问题的对称性,选取1/4板进行分析,将其划分为30×30×6的粗网格和150×150×30的细网格.

为了验证算法的正确性,图2和图3列出了两种加载方式下板(x1=(1/4)h,x2=(1/4)h)处u1、u3和φ的混合扩展多尺度有限元解(MEMsFEM)、常规有限元粗网格解(FEM-CM)、常规有限元细网格解(FEM-FM)及精确解[15].

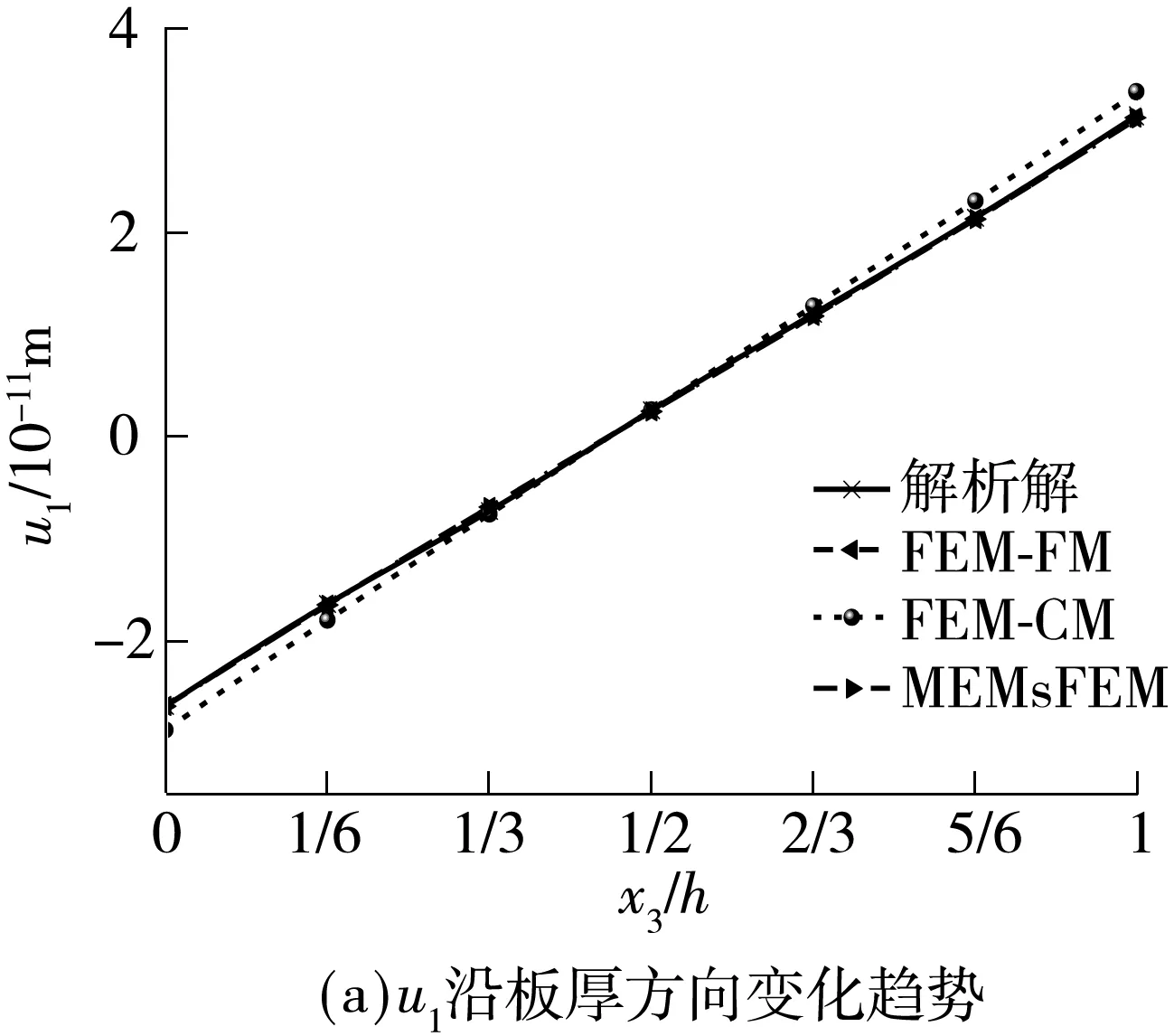
图2 板x1=x2=(1/4)h处u1、u3和φ沿板厚方向变化趋势(工况1)

Fig.2 Variation ofu1、u3andφwith coordinatex3at locationx1=x2=(1/4)h(Case1)

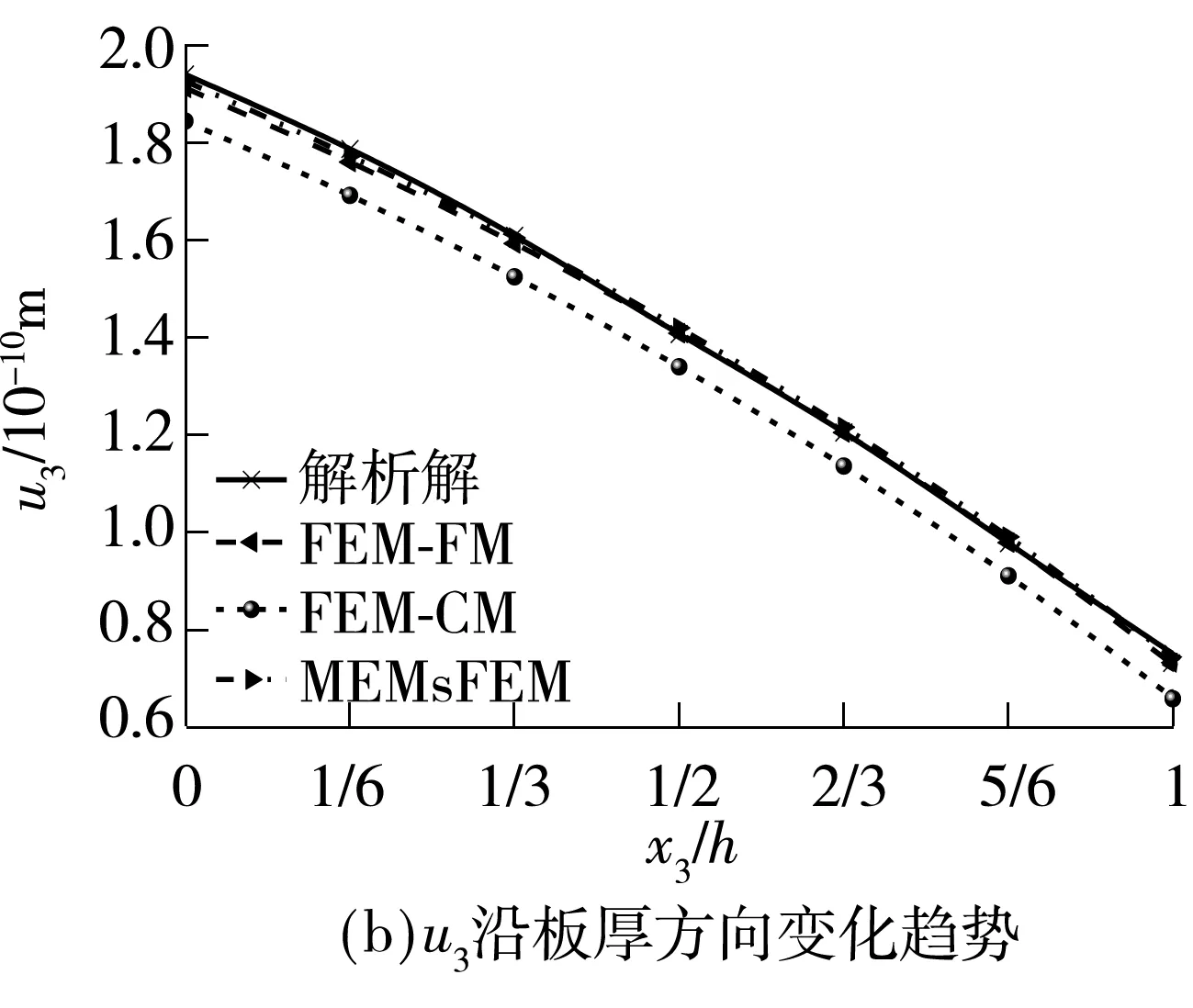
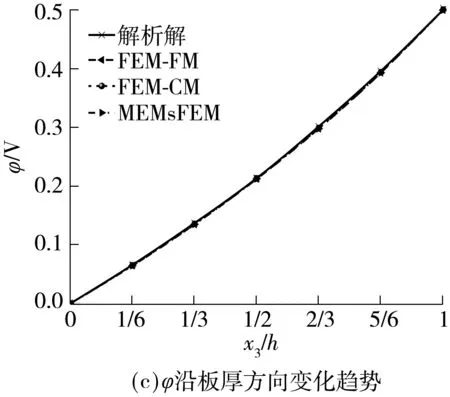
图3 板x1=x2=(1/4)h处u1、u3和φ沿板厚方向变化趋势(工况2)

Fig.3 Variation ofu1、u3andφwith coordinatex3at locationx1=x2=(1/4)h(Case2)

从图2和图3可以看出:文中提出的混合扩展多尺度有限元解和常规有限元细网格解同问题的精确解吻合得非常好,而常规有限元粗网格解由于粗网格无法解析材料的非均质性所以结果精度较低.由此可见:文中构造的多尺度基函数可以有效捕捉材料的微观非均质信息,在相同网格密度下混合扩展多尺度有限元法能得到比传统有限元法更好的计算精度.

图4和图5为工况1和工况2两种加载条件下混合扩展多尺度有限元法和在细网格上计算的传统有限元法(参照解)结果的比较图.在工况1下:

u1、u3和φ的极值误差分别为0.068%、0.26%和0.44%;在工况2下:u1、u3和φ的极值误差分别为3.75%、0.52%和0.00%.此外，在整个研究区域内两种算法u1、u3和φ的结果云图非常接近,由此进一步验证了混合扩展多尺度有限元法的正确性.

为了验证混合扩展多尺度有限元法的高效性,将该算法和在细网格上计算的传统有限元法的计算耗时进行对比,其运行时间分别为:1 222.87 s和6 242.08 s,文中所提算法的耗时仅为传统有限元法的19.6%,因此混合扩展多尺度有限元法明显提高了计算的效率.

4 结论

文中采用混合扩展多尺度有限元法对功能梯度压电板力电耦合问题进行了求解.算例分析结果表明：混合扩展多尺度有限元法通过构造多尺度基函数有效地捕捉了材料各物理参数在空间上的梯度变化性,利用粗网格宏观矩阵的组装将两场的微观信息及场间的耦合作用同时映射到宏观尺度上,使问题可以在粗尺度网格上求解并得到同精确解一致的结果,由此验证了算法的正确性；在保证计算精度的前提下,混合扩展多尺度有限元法明显比在细网格上计算的传统有限元法节省计算时间.

[1] WU C,KAHN M,MOY W.Piezoelectric ceramics with functional gradients:a new application in material design [J].Journal of the American Ceramic Society,1996,79(3):809- 812.

[2] ZHU X,WANG Q,MENG Z.A functionally gradient piezoelectric actuator prepared by powder metallurgical process in PNN-PZ-PT system [J].Journal of Materials Science Letters,1995,14(7):516- 518.

[3] BEHJAT B,KHOSHRAVAN M R.Geometrically nonlinear static and free vibration analysis of functionally graded piezoelectric plates [J].Composite Structures,2012,94(3):874- 882.

[4] SINA S A,NAVAZI H M,HADDADPOUR H.An analytical method for free vibration analysis of functionally graded beams [J].Materials & Design,2009,30(3):741- 747.

[5] 蒋正文,沈孔健,万水.基于分层线性离散模型的 FGM 板断裂力学分析 [J].华南理工大学学报(自然科学版),2014,42(4):77- 84. JIANG Zheng-wen,SHEN Kong-jian,WAN Shui.Fracture mechanics analysis of FGM plates based on layered linear discrete model [J].Journal of South China University of Technology(Natural Science Edition),2014,42(4):77- 84.

[6] ASEMI K,ASHRAFI H,SALEHI M,et al.Three-dimensional static and dynamic analysis of functionally graded elliptical plates,employing graded finite elements [J].Acta Mechanica,2013,224(8):1849- 1864.

[7] HOU T Y,WU X H.A multiscale finite element method for elliptic problems in composite materials and porous media [J].Journal of Computational Physics,1997,134(1):169- 189.

[8] 李霄琳.非均质材料的光滑多尺度有限元法研究 [D].长春:吉林大学,2015.

[9] 孟广伟,李霄琳,周立明.裂隙岩体渗流的光滑多尺度随机配点法 [J].水利学报,2015,46(1):34- 41. MENG Guang-wei,LI Xiao-lin,ZHOU Li-ming.Smoothed multiscale stochastic collocation method for flow in fractured rocks [J].Journal of Hydraulic Engineering,2015,46(1):34- 41.

[10] ZHANG H W,WU J K,FU Z D.Extended multiscale finite element method for elasto-plastic analysis of 2D periodic lattice truss materials [J].Computational Mechanics,2010,45(6):623- 635.

[11] ZHANG S,YANG D S,ZHANG H W,et al.Coupling extended multiscale finite element method for thermoelastic analysis of heterogeneous multiphase materials [J].Computers & Structures,2013,121:32- 49.

[12] LÜ J,ZHANG H W,CHEN B S.Shape and topology optimization for closed liquid cell materials using extended multiscale finite element method [J].Structural and Multidisciplinary Optimization,2014,49(3):367- 385.

[13] 刘银,张洪武,张盛,等.基于扩展多尺度有限元非均质材料的屈曲分析 [J].固体力学学报,2013,33(10):20- 26. LIU Yin,ZHANG Hong-wu,ZHANG Sheng,et al.Extended multiscale finite element method for the bucking of heterogeneous materials [J].Chinese Journal of Solid Mechanics,2013,33(10):20- 26.

[14] ZHANG H W,LIU Y,ZHANG S,et al.Extended multiscale finite element method:its basis and applications for mechanical analysis of heterogeneous materials [J].Computational Mechanics,2014,53(4):659- 685.

[15] ZHONG Z,SHANG E T.Three-dimensional exact analysis of a simply supported functionally gradient piezoelectric plate [J].International Journal of Solids and Structures,2003,40(20):5335- 5352.

Electromechanical Coupling Analysis of Functionally Graded Piezoelectric Plate Based on MEMsFEM

MENGGuang-wei1LIXiao-lin2ZHOULi-ming1LIFeng1WANGHui1

(1.School of Mechanical Science and Engineering, Jilin University, Changchun 130022, Jilin, China; 2.College of Construction Engineering, Jilin University, Changchun 130026, Jilin, China)

Functionally graded piezoelectric material(FGPM) is an electromechanical coupling material of conti-nuous property variation.Due to the heterogeneity of the FGPM property, investigating the mechanics of this material has posed a great challenge.In this paper, an analytical model describing the electromechanical coupling of the FGPM is constructed based on the mixed extended multi-scale finite element method(MEMsFEM).In the model, the multi-scale base functions of electrical fields are set up by using the traditional multi-scale finite element method, and the multi-scale base functions of displacement fields in different directions are set up by using the extended multi-scale finite element method.Moreover, the coupling terms are introduced to model the coupling among the displacement fields in different directions.Since constructing multi-scale base functions helps capture the material heterogeneity effectively, it is feasible to solve the problem in a coarse grid scale, which can significantly reduce the computation amount.Finally, the proposed method is proved to be effective and efficient by numerical examples.It is thus concluded that the proposed method provides an effective approach to simulating the mechanical behaviors of functionally graded materials.

mixed extended multi-scale finite element method; functionally graded materials; piezoelectric material; electromechanical coupling

2014- 10- 28

国家重大科学仪器设备开发专项(2012YQ030075)；国家自然科学基金资助项目(51305157)；吉林省科技厅基金资助项目(20160520064JH) Foundation items: Supported by the National Key Scientific Instrument and Equipment Development Projects of China(2012YQ030075),the National Natural Science Foundation of China(51305157) and Jilin Provincial Department of Science and Technology Fund Project(20160520064JH)

孟广伟(1959-)，男，教授，博士生导师，主要从事疲劳与断裂研究.E-mail：mgw@jlu.edu.cn

† 通信作者: 周立明(1982-)，男，博士，副教授，主要从事计算固体力学研究.E-mail：lmzhou@jlu.edu.cn

1000- 565X(2016)10- 0081- 06

TB 115

10.3969/j.issn.1000-565X.2016.10.012