横观各向同性岩土材料应变局部化现象的有限元模拟*

常江芳 徐远杰 楚锡华

(1.武汉大学 工程力学系， 湖北 武汉 430072； 2.石家庄铁道大学 工程力学系, 河北 石家庄 050043)

横观各向同性岩土材料应变局部化现象的有限元模拟*

常江芳1，2徐远杰1†楚锡华1

(1.武汉大学 工程力学系， 湖北 武汉 430072； 2.石家庄铁道大学 工程力学系, 河北 石家庄 050043)

岩土材料的各向异性性质与其微结构紧密相关，文中考虑到内摩擦角是应力状态、组构张量及材料主方向的函数，发展了适用于横观各向同性岩土材料的修正的Drucker-Prager屈服准则.基于Cosserat连续体理论，推导了该准则的一致性映射返回算法，形成了一致性切线模量矩阵，并利用有限元软件Abaqus的用户单元子程序(UEL)进行了数值实现.通过将积分点材料强度随材料主方向及各向异性程度的变化关系与理论结果进行比较，验证了程序开发的正确性.数值算例重点分析了材料主方向和各向异性参数对结构极限承载力及破坏模式的影响，且与经典连续体的结果进行了比较.结果表明，文中方法能够较好地模拟具有横观各向同性的岩土材料的应变局部化现象.

岩土材料；岩土力学；横观各向同性；Cosserat连续体；屈服准则；应变局部化

自然界的岩土材料一般均呈现很强的各向异性.各向异性又分为固有各向异性和诱导各向异性.由于其沉积过程、孔隙、裂纹等固有属性而使其在原位状态下表现出的各向异性称为固有各向异性；岩土材料在非比例加载或塑性变形的影响下，由于主应力方向不断变化，导致其细观结构发生演化而表现出的各向异性称为诱导各向异性.关于此两种各向异性，国内外学者做了相关的理论及实验研究[1- 3]，提出了多种各向异性屈服准则[4- 7].姚仰平等[4]以横观各向同性土为例，阐述了同时考虑材料外部应力分布与材料内部强度分布下各向异性土的破坏机制.贾乃文[5]以Hill正交异性屈服准则为基础，讨论了横观各向同性条件下，岩土中出现塑性屈服的Drucker准则修正表达式.Duveau等[6]对一些强各向异性材料的屈服准则做了一个综合评价.Gao等[7]在屈服函数的摩擦系数中引入了一个各向异性变量，考虑它为应力不变量及微结构张量的联合不变量的函数，提出了一个适用于横观各向同性材料的屈服准则.然而基于唯象方法提出的各向异性屈服准则一般包含较多的材料参数，且这些参数与材料微观结构之间的关系不明确.Pietruszczak等[8- 9]提出了一个各向异性屈服准则，基于物质点给出了各向异性程度及加载方向对材料强度影响的理论分析，其材料参数是应力和微结构张量联合不变量的显式函数，使得实验验证更易实现.余天堂等[10- 11]基于Pietruszczak等[8- 9]提出的各向异性屈服准则，考虑各向异性参数和单轴抗压强度是一个由微结构张量和加载方向表示的分布函数，给出了沉积岩的一种各向异性模型.Zhong等[12]对Pietruszczak-Morz屈服准则中的材料参数进行了分析.在Pietruszczak等[8- 9]的研究基础上，Lade[13- 15]推导了一个基于 Lade 强度准则的各向异性强度准则，并展开了相应的理论及实验研究.

然而上述研究多关注的是对各向异性破坏准则的描述，是各向异性对一个物质点破坏的影响.关于各向异性对结构承载力及破坏模式影响的数值模拟仍相对较少.Chu等[16]在Pietruszczak等[8- 9]提出的各向异性屈服准则的基础上，考虑内摩擦角为组构张量、应力状态及材料主方向的函数，对Drucker-Prager屈服准则进行了修正，以横观各向同性材料为例研究了各向异性对应变局部化的影响，然而不足之处是其基于经典连续体理论，在伴随应变软化出现应变局部化现象的同时会产生网格依赖性.为克服这一问题，文中基于Cosserat连续体理论[17- 19]，推导了修正的Drucker-Prager屈服准则的一致性映射返回算法及切线模量矩阵，重点分析了材料主方向和各向异性程度对横观各向同性材料极限承载力及破坏模式的影响，最后通过与经典连续体计算结果进行比较来验证解决网格依赖性问题的有效性.

1 基于Cosserat连续体的横观各向同性弹塑性模型

1.1 Cosserat连续体的基本方程

与经典连续体相比，Cosserat连续体中引入了独立的转动自由度，平面应变情况下，其位移矢量u可表示为[17]

u=[uxuyωz]T

(1)

其中，ux、uy为平动位移，ωz为独立的转动位移.

应变矢量ε除了与经典意义上所对应的正应变和剪应变有关以外，还包含两个微曲率，如下所示：

ε=[εxεyεzεxyεyxlcκxzlcκyz]T

(2)

其中：

(3)

可以看到这里引入了一个内部长度参数lc，保证了Cosserat连续体的控制方程在计算过程中的正定性，可有效克服网格依赖性问题.

几何方程可表示如下：

ε=Lu

(4)

其中，

(5)

Cosserat连续体的应力矢量σ引入了两个偶应力mxz和myz(如图1所示)：

(6)

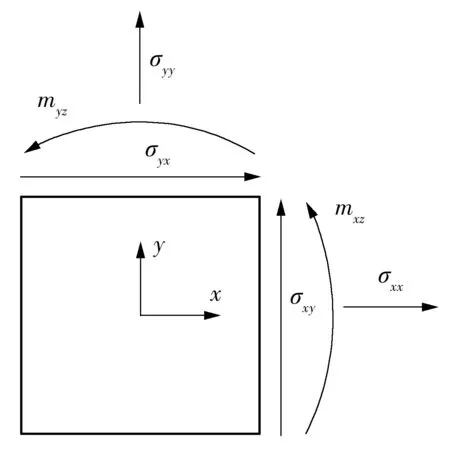
图1 平面应变条件下应力及偶应力示意图

Fig.1 Sketches of stress and couple stress under strain plane condition

弹性应力-应变关系可以表示为

σ=Deε

(7)

其中本构矩阵为

(8)

准静态条件下，若忽略体积力及体力偶的影响，则平衡方程可表示为

LTσ=0

(9)

1.2 修正的Drucker-Prager准则

适用于各向同性材料的Drucker-Prager准则以应力不变量的形式表示为

F=q+Aφp+Bφ=0

(10)

其中,p和q可分别用应力第一不变量及偏应力第二不变量表示如下:

(11)

(12)

其中，P矩阵可表示为

(13)

式(10)中参数Aφ、Bφ为内摩擦角φ和黏聚力c的函数，若Drucker-Prager准则为Mohr-Coulomb准则的内接圆，则可将其分别表示为

(14)

通常对黏聚力考虑线性硬化或软化，即

(15)

基于应力不变量与组构张量，Pietruszczak与Mroz给出了一个能够描述各向异性材料的屈服准则[8]：

η=η0(1+Ωijlilj)

(16)

其中：η为描述屈服函数的材料参数，与应力状态有关；η0为η的平均值；Ωij为描述η偏离η0程度的偏量.对正交各向异性材料Ωij有两个不等的特征值，对横观各向同性材料，其可用一个标量描述，对各向同性材料，Ωij为零，此时η=η0.li、lj为相对于材料主轴的加载方向.式(16)也可用Ωij的主值表示为

(17)

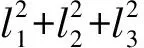
(18)

图2 材料主方向示意图

加载向量按如下方式计算：

(19)

为了简化，仅考虑内摩擦角的各向异性，即令

(20)

则有

(21)

式(10)、式(3)、式(1)构成了描述横观各向同性材料的屈服函数.

对于岩土材料，通常采用非关联流动法则，塑性势可取为

G=q+Aψp+Bψ

(22)

类似地：

(23)

其中，ψ为膨胀角.

由一致性算法最终得到更新后的应力[17- 18]，

(24)

其中：

(25)

(26)

(27)

(28)

其中FE=qE+AφpE+BE.

(29)

以及一致性弹塑性切线模量矩阵：

(30)

其中:

(31)

(32)

可以验证，当采用关联流动法则时，该矩阵具有主对称性.

2 数值算例

以Abaqus软件的UEL子程序接口为平台，对文中发展的单元类型和弹塑性本构模型进行了数值实现[20].以平板压缩模型为例，单元类型为平面应变8节点减缩单元，模型尺寸为0.6m×0.8m，上下边界约束x方向自由度，左右边界自由，上下边界施加对称均布位移荷载uy，如图3(a)所示.计算中所采用的材料参数如表1所示.

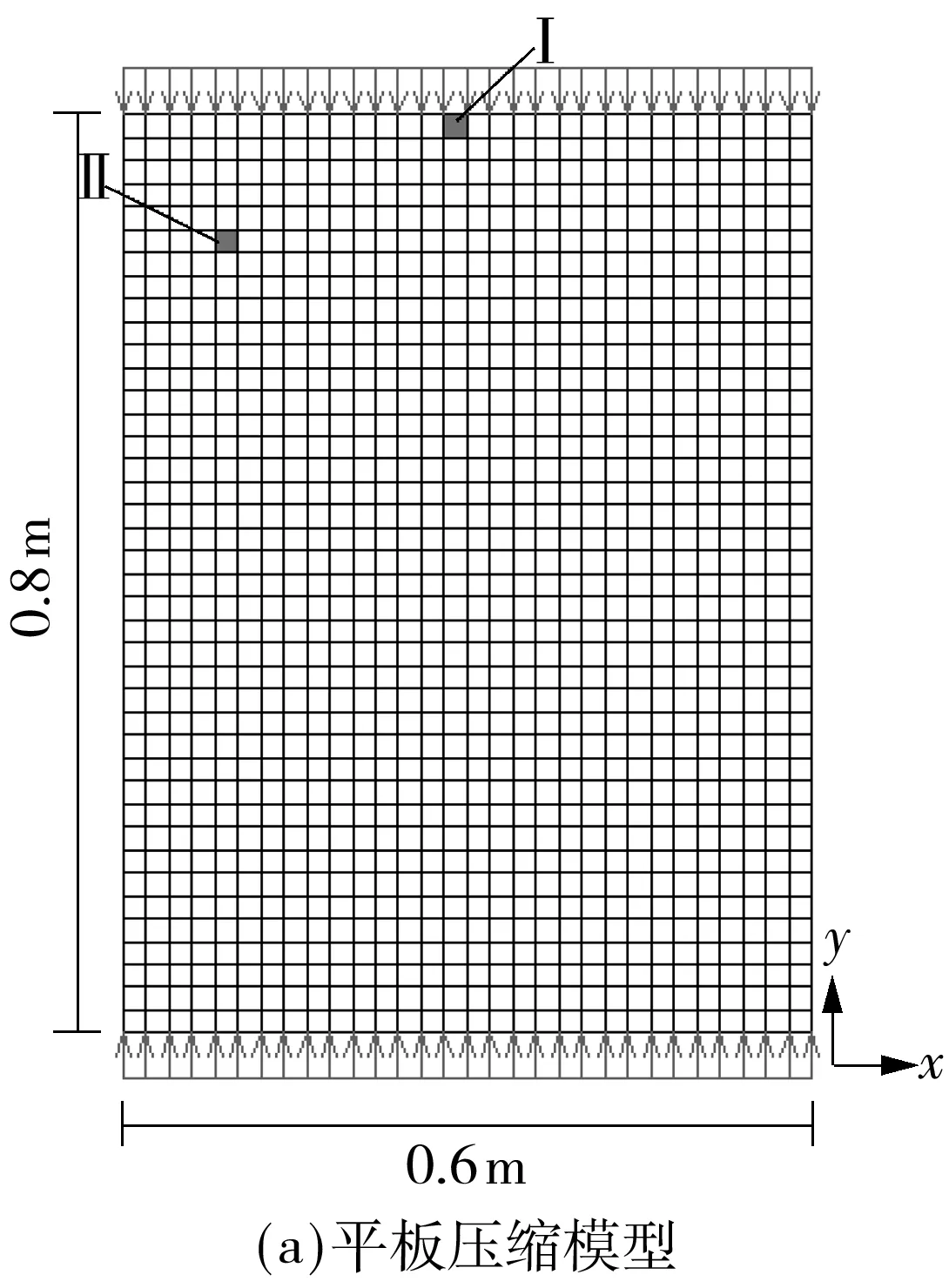
图3 有限元模型

参数数值参数数值E/Pa30×106c0/Pa0．06×106υ0．3hcp/Pa0．01×106β/(°)0～180Ω10、-0．05、-0．1、-0．15φ/(°)20Gc/Pa10×106ψ/(°)15lc/m0．02

1)E为弹性模量；υ为泊松比；β为材料主方向角.

Pietruszczak等[8]基于他们提出的各向异性屈服准则对横观各向同性材料物质点的理论分析显示，对于不同的加载方向，材料轴向强度随Ω1的演化规律不同，存在一个转折点，该点材料的轴向强度将独立于各向异性程度，且Zhong等[12]证明了此转折点所对应的材料主方向与材料固有属性有关.这里，为与已有理论结果进行对比，选取了结构的两个代表性单元，标号为Ⅰ和Ⅱ，分别位于板上边缘中间位置和剪切带附近，如图4所示，给出了两个单元1号积分点(见图3(b))上等效应力随加载位移的变化曲线，其中参数取β=30°，Ω1=-0.1.易知峰值qmax代表了该点的强度，图5(a)和5(b)则给出了积分点(物质点)上归一化的材料强度随各向异性程度及材料主方向的变化趋势，可见其趋势与已有理论结果[8]较为吻合(见图5(c),其中法向强度ζ=Δσ1/(2σ0))，从而验证了本程序开发的正确性.下面主要就材料主方向β及各向异性程度Ω1对结构极限承载力及破坏模式的影响做详细分析.

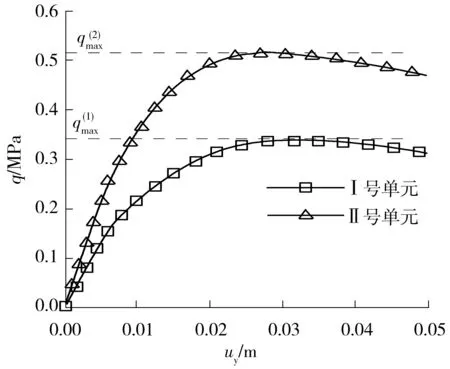
图4 积分点等效应力随加载位移变化曲线

Fig.4 Curves of the equivalent stress versus the loading displacement in the integration points

2.1 材料主方向β的影响

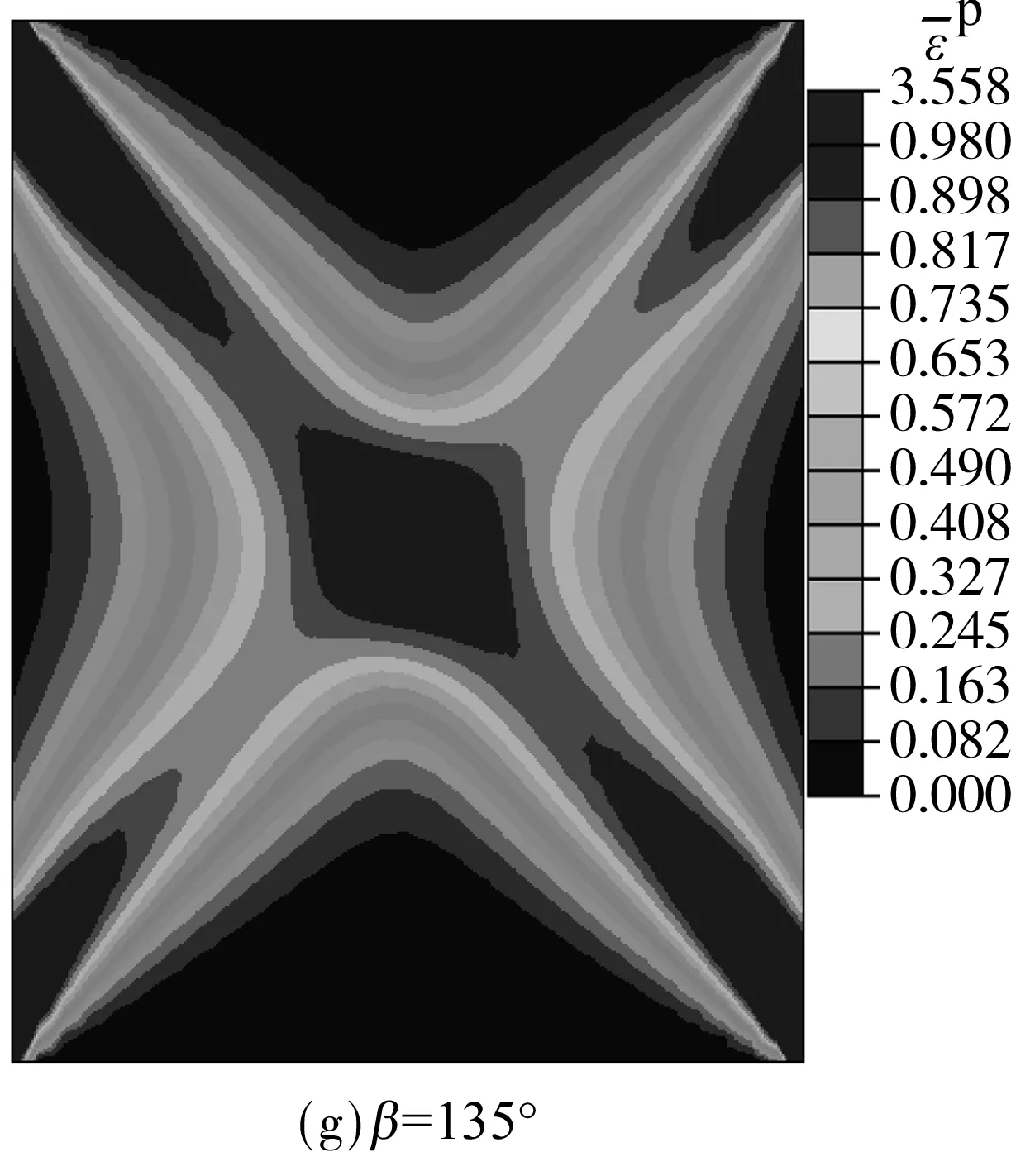
由图2可知，β为各向同性面相对x轴逆时针转动的角度，描述了材料主轴相对整体坐标系的偏移，β的改变也可理解为加载方向的改变.图6为Ω1=-0.10，加载位移为0.05 m时等效塑性应变分布云图.值得注意的是，Ω1取负值意味着各向同性面法向(e(2)方向)有较大的摩擦强度[14].可以看出剪切带呈现了X型分布，当β=0°和β=90°时，由于加载方向和材料主方向保持一致或垂直，剪切带呈对称分布，如图6(a)和6(e)所示.当β≠0°和β≠90°时，剪切带两个分支呈现不对称性，沿各向同性面方向的剪切带较宽，等效塑性应变值较高，文中称之为强剪切带，与之共轭的另一条剪切带称为弱剪切带，如图6(b)和6(h)所示，与姚仰平等[4]的理论分析相比，其破坏面的位置可能就是强剪切带出现的位置，数值模拟显示还存在一个弱剪切带，只是在破坏时强剪切带占据了主导地位.由图6(b)-6(d)可见，当0°<β<90°时剪切带呈“/”型分布，且随着β的增大“/”方向剪切带逐渐变宽.反之，当90°<β<180°时，剪切带呈“”型分布，且随着β的增大“”方向剪切带逐渐变窄.对于一对互补的β角，如β=30°和β=150°，等效塑性应变峰值相等，但剪切带分布模式相反.随着β从0°演化到180°，强剪切带上等效塑性应变峰值出现了增大-降低-增大-降低的对称过程，弱剪切带则具有互补的变化过程，如图7所示.

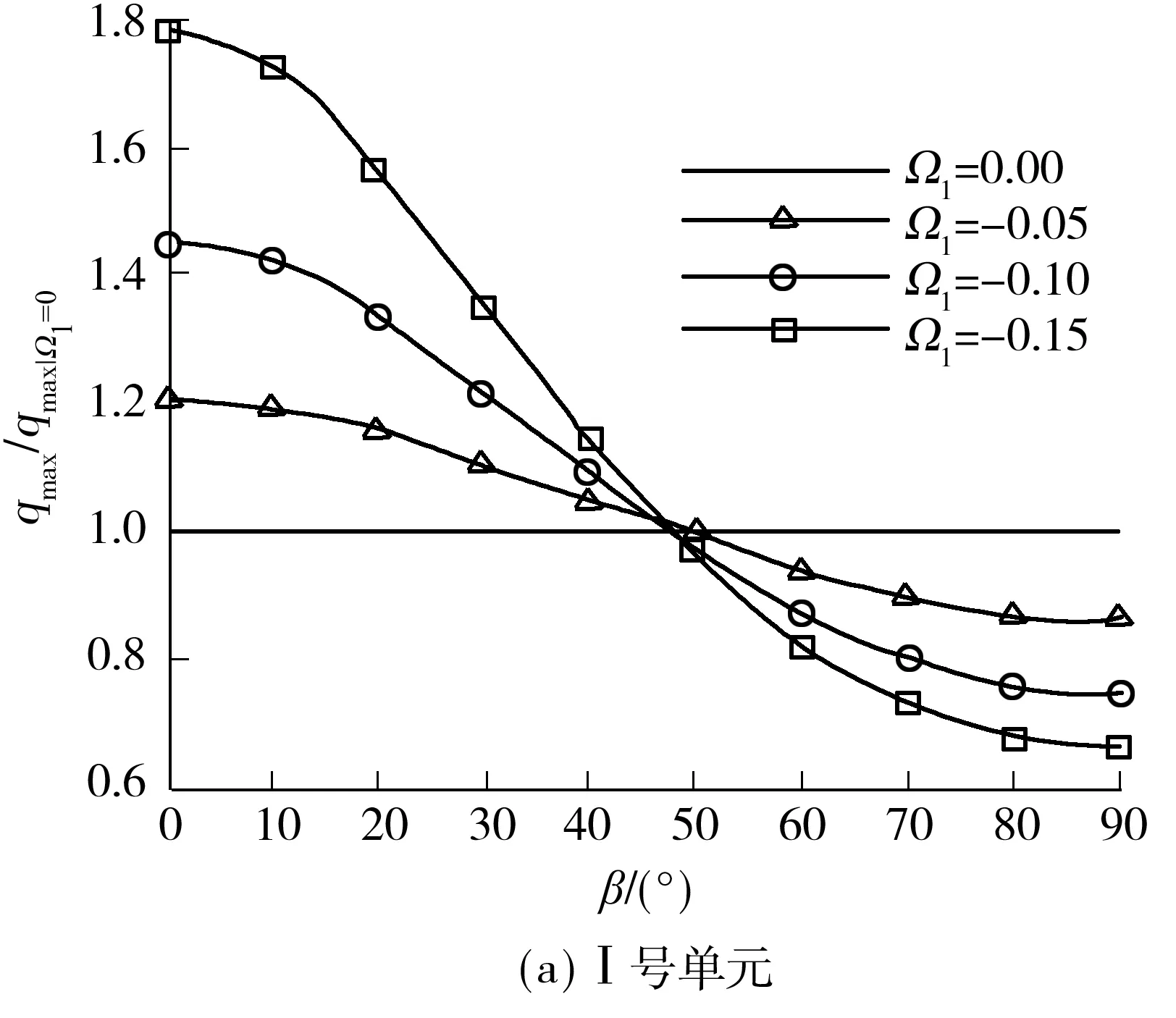
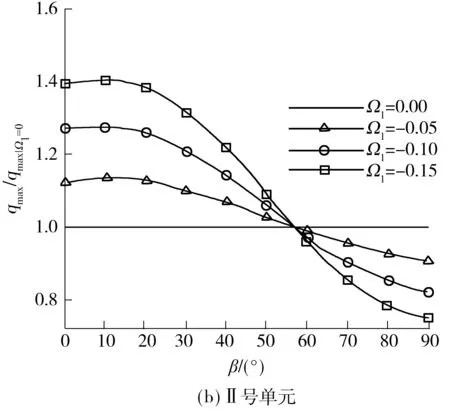
图5 积分点材料强度随材料主方向β及各向异性程度Ω1的变化曲线

Fig.5 Variation curves of material strength withβandΩ1in integration points

图8给出了随β变化材料的承载力-位移曲线,可以清楚地看到当各向同性面位于水平位置，即β=0°时，结构承载力最大，随着β的增大承载力逐渐降低，90°时最低，这与横观各向同性材料屈服准则中摩擦强度参数各向异性的分布规律一致.

2.2 各向异性参数Ω1的影响

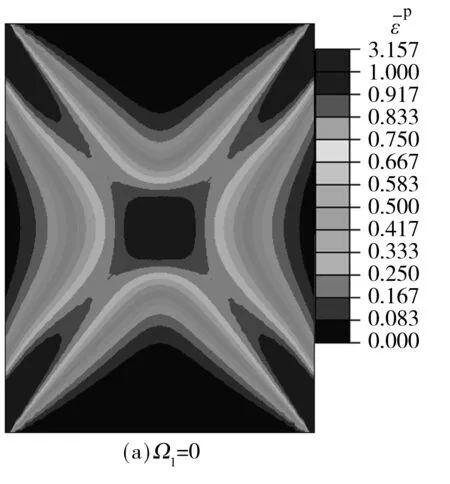
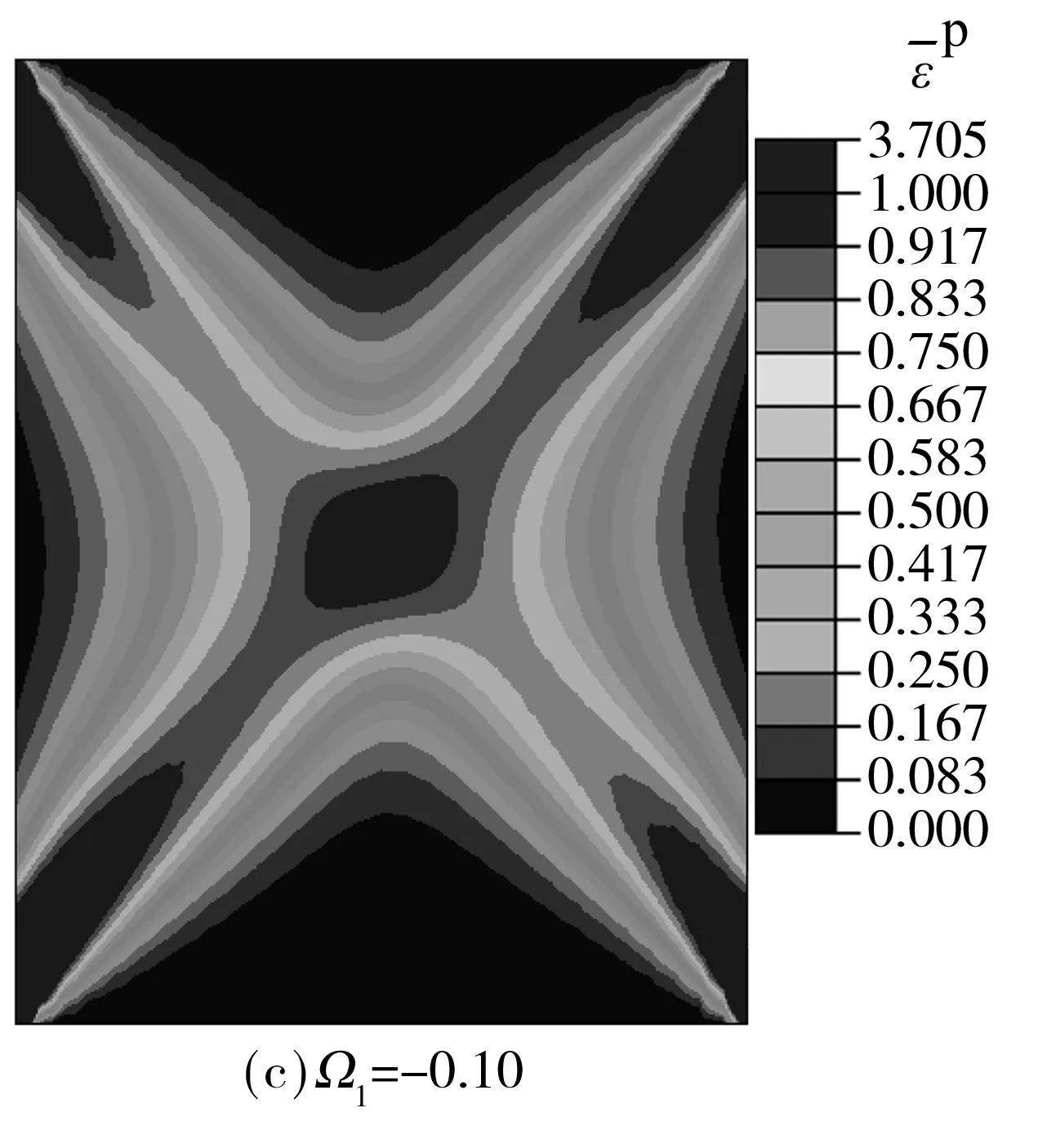
如前所述，Ωij为描述η偏离η0程度的偏张量，对于横观各向同性材料可以用一个标量Ω1来描述.需指出文中各向异性参数取值来自于文献[8]，依次取Ω1=0，-0.05，-0.1,-0.15,β=30°,加载位移为0.05 m，其他参数同表1.

图9给出了等效塑性应变随各向异性程度变化的结果.可以看出，各向异性程度越大，X型剪切带的非对称性越强，强剪切带等效塑性应变的峰值越大，弱剪切带峰值则越小.图10为承载力-位移曲线，随着Ω1绝对值的增大结构承载力逐渐增大.这里同时给出了归一化的承载力随各向异性程度及材料主方向的综合变化规律，如图11所示，其中，纵轴表示各承载力峰值除以Ω1=0时的承载力峰值，可见结构整体响应亦呈现出了与图5类似的规律，即在β约为47°的位置出现转折点，β小于该值时，结构承载力随Ω1绝对值的增大而增大，大于该值时则相反.

图7 强剪切带和弱剪切带上等效塑性应变峰值变化规律

Fig.7 Variation of the peak value of equivalent plastic strain in the intense shear band and the weak shear band

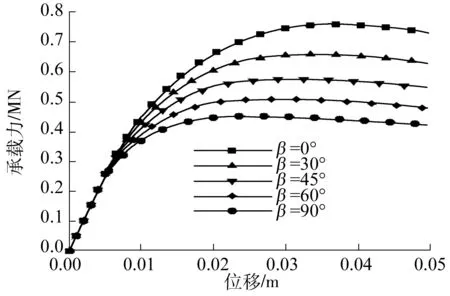
图8 不同材料主方向承载力-位移曲线

Fig.8 Curves of load-displacement with different material direction

图10 不同各向异性程度下承载力-位移曲线

Fig.10 Curves of load-displacement with different anisotropic degrees

2.3 网格依赖性调查

基于经典连续体理论，采用有限单元法计算弹塑性问题，当应变软化和局部化现象发生时，不可避免地会出现网格依赖性问题.本节通过对经典连续体和Cosserat连续体两种理论框架下的计算结果进行比较，调查了有限元计算的网格依赖性问题.

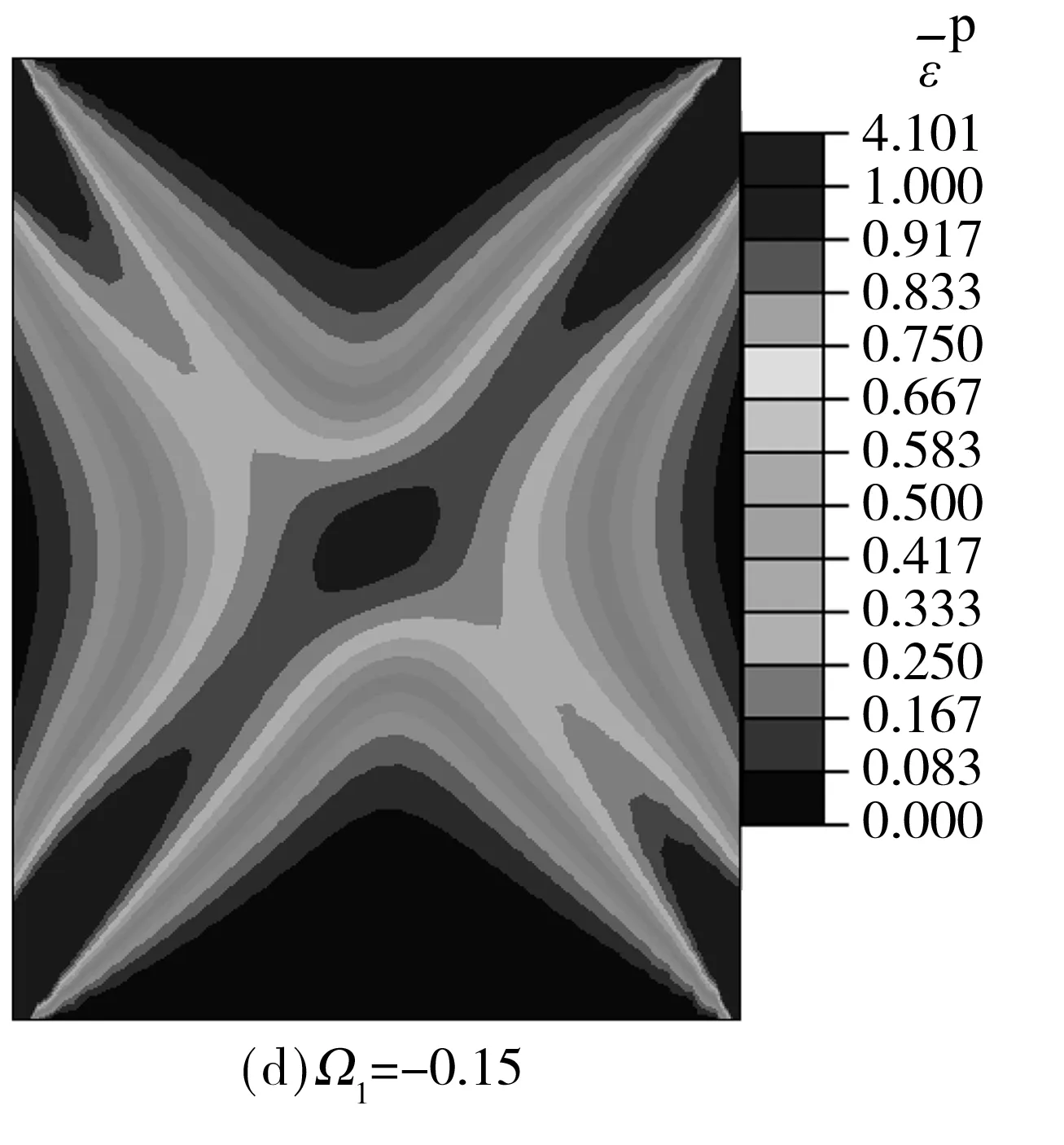
图9 等效塑性应变分布(β=30°)

图11 结构承载力随材料主方向β及各向异性程度Ω1的变化

Fig.11 Variation of bearing capacity of structure withβandΩ1

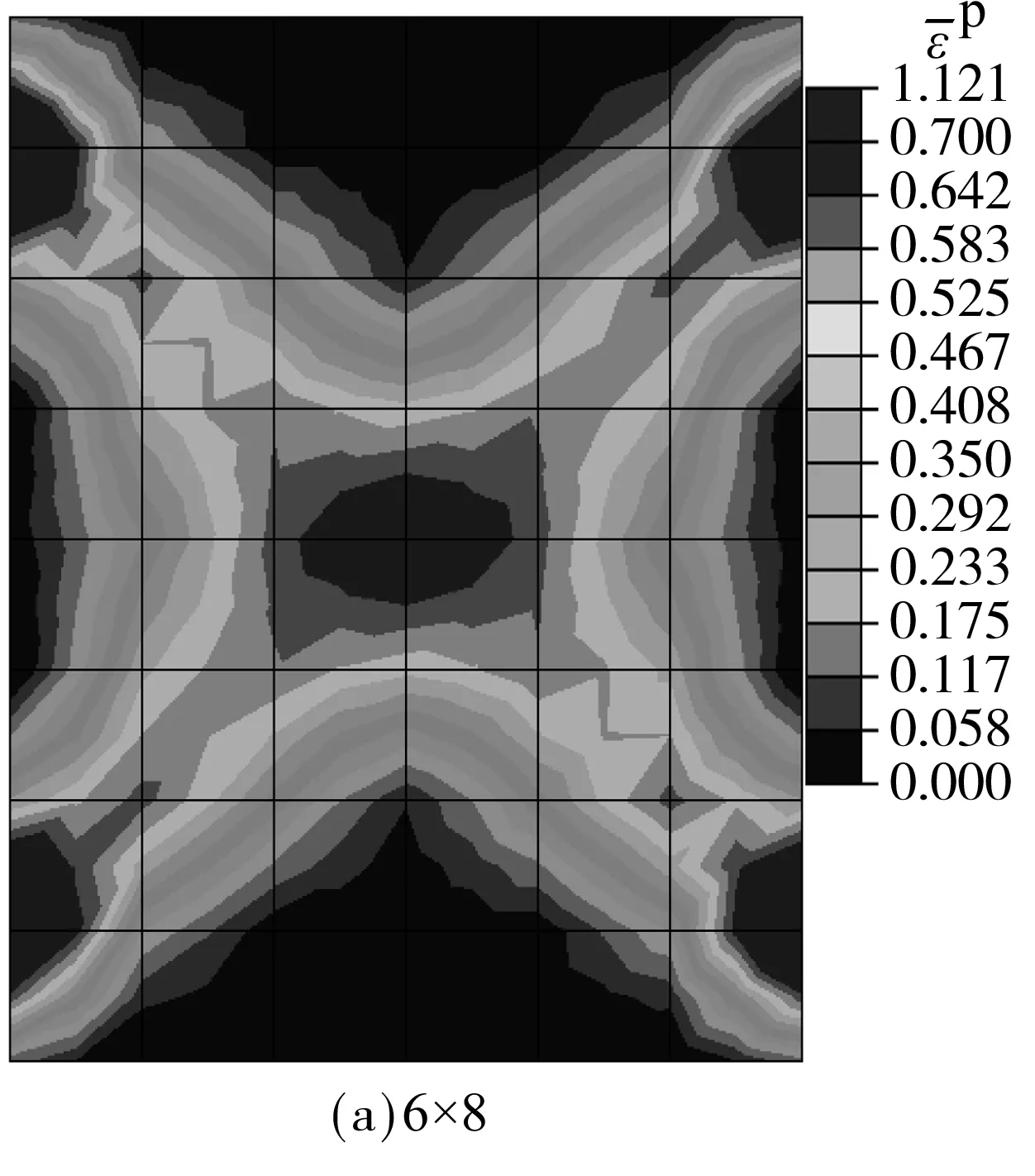
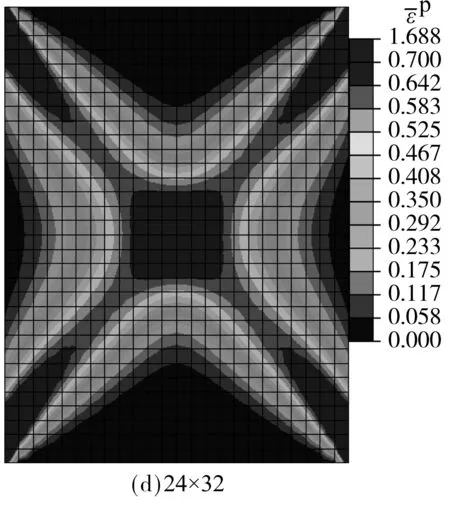
取材料主方向β=90°，Ω1=-0.1，其他材料参数同表1，网格密度分别取6×8，12×16，18×24，24×32，30×40，60×80进行比较.图12给出了基于经典连续体等效塑性应变分布图，可以看到随着网格加密，等效塑性应变的峰值逐渐增大，且剪切带宽度明显变窄.图13显示结构极限承载力随网格密度增大而逐渐降低，且模拟软化段的能力亦逐渐降低.图14则为基于Cosserat连续体得到的等效塑性应变分布图，随着网格加密，等效塑性应变峰值有所增大但剪切带宽度基本保持不变.图15显示虽然结构承载力有些许降低，但其变化越来越小，计算结果最终收敛于较为接近的值.需说明的是，图中网格为6×8时计算结果与其他结果相比差异较大，这是由于网格稀疏到一定程度，有限元计算本身的误差所致.经过比较可见引入Cosserat连续体后，网格依赖性问题得到了有效的解决.

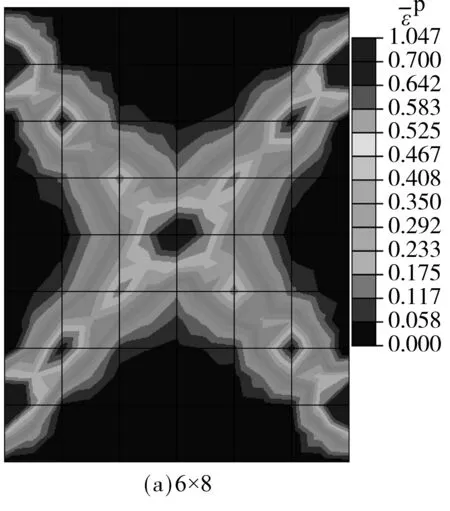
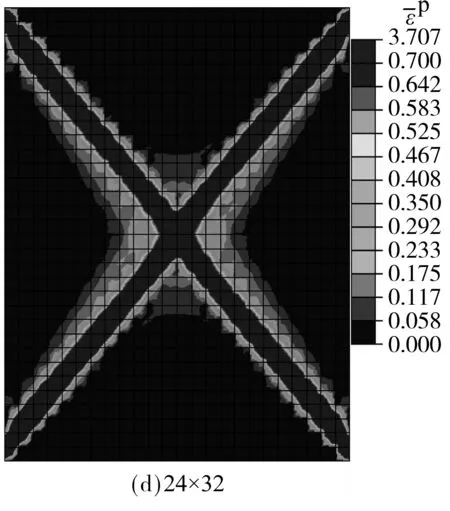
图13 经典连续体不同网格密度承载力-位移曲线

Fig.13 Curves of load-displacement with different mesh density based on classical continuum theory

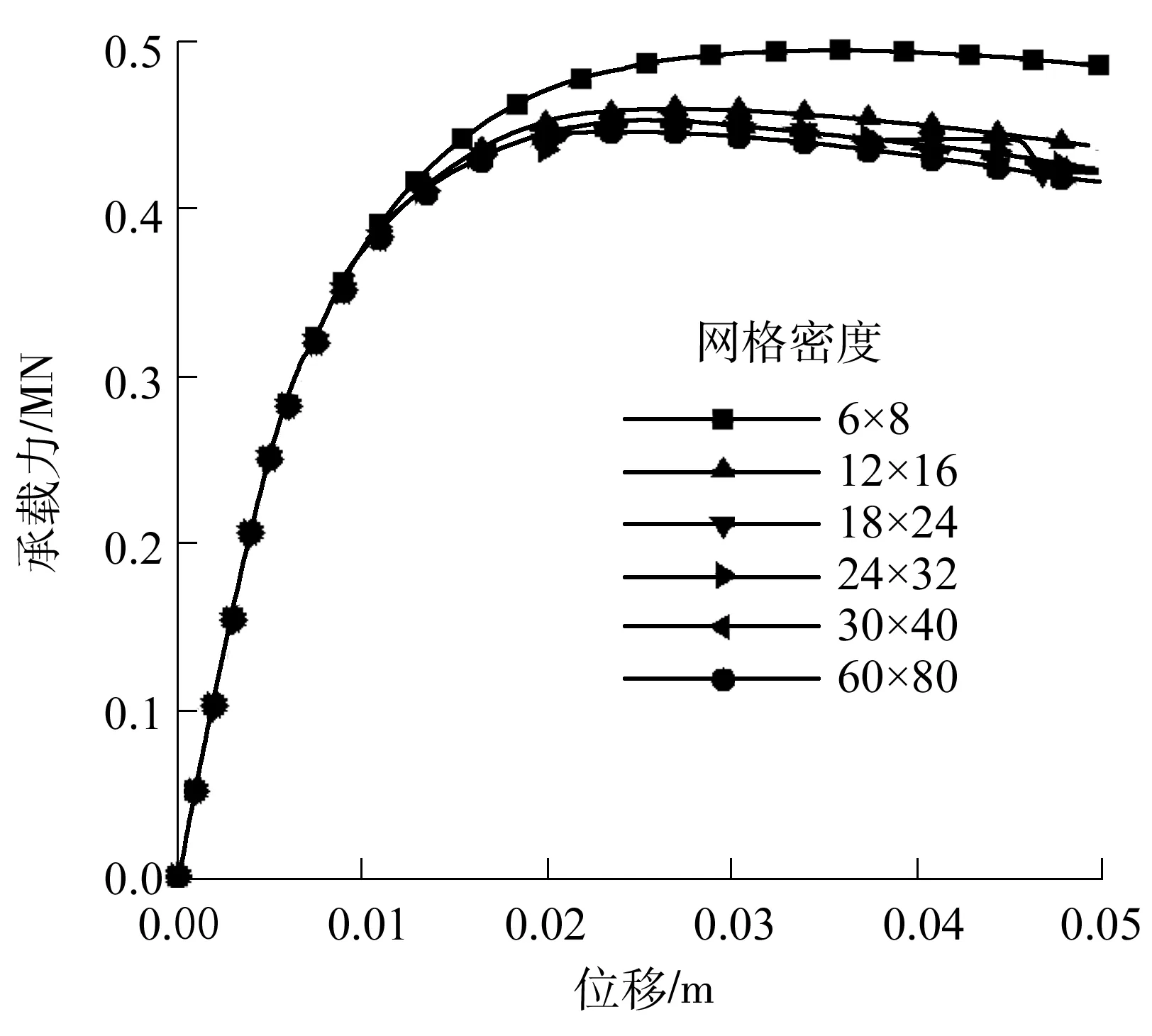
图15 Cosserat连续体不同网格密度承载力-位移曲线

Fig.15 Curves of load-displacement with different mesh density based on Cosserat continuum theory

3 结论

基于Pietruszczak 和 Mroz提出的各向异性屈服准则，考虑摩擦角为材料主方向及应力张量与微结构张量联合不变量的函数，提出了一个适用于横观各向同性岩土材料的修正的Drucker-Prager屈服准则，并基于Cosserat连续体推导了其一致性映射返回算法和切线模量矩阵.数值算例重点分析了材料主方向及各向异性程度对结构极限承载力及破坏模式的影响，结果表明：

(1)材料主方向β=0°或β=90°时剪切带呈对称分布，前者结构承载力最大，后者最低.0°<β<90°时，随β增大，剪切带逐渐变宽，结构承载力逐渐降低，90°<β<180°则相反.β从0°到180°，强剪切带等效塑性应变峰值经历了增大-降低-增大-降低的对称过程，弱剪切带则相反.β互补时剪切带呈现相反的分布模式.

(2)Ω1绝对值越大，材料各向同性面的强度越低；对于β≠0°、β≠90°的非对称情况，剪切带呈现的X型分布的非对称性更强.承载力变化趋势存在一个转折点，约为β=47°，β小于该值时，结构承载力随Ω1绝对值的增大而增大，β大于该值时则相反.

(3)与经典连续体的模拟结果比较表明，文中基于Cosserat连续体的数值方法较好地解决了网格依赖性问题.

[1] ARTHUR J R F,Menzies B.Inherent anisotropy in a sand [J].Geotechnique,1972,22(1):115- 128.

[2] ARTHUR J R F,CHUA K S,DUNSTAN T.Induced anisotropy in a sand [J].Geotechnique,1979,27(1):13- 30.

[3] ODA M.Inherent and induced anisotropy in plasticity theory of granular soils [J].Mechanics of Materials,1993,16(1/2):35- 45.

[4] 姚仰平,祝恩阳.横观各向同性土的简明破坏机制解释 [J].岩土力学,2014,35(2):328- 333. YAO Yang-ping,ZHU En-yang.Concise interpretation of damage mechanism for cross-anisotropic soil [J].Journal of Geotechnical Mechanics,2014,35(2):328- 333.

[5] 贾乃文.岩土工程中横观各向同性Drucker屈服准则 [J].华南理工大学学报(自然科学版)，1993,21(2):49- 54. JIA Nai-wen.Drucker yield criterion of horizontally isotropic rock and soil [J].Journal of South China University of Technology(Natural Science Edition),1993,21(2):49- 54.

[6] DUVEAU G,SHAO J F,HENRY J P.Assessment of some failure criteria for strongly anisotropic materials [J].Mechanics of Cohesive-Frictional Materials,1998,3(1):1- 26.[7] GAO Z W,ZHAO J D,YAO Y P.A generalized anisotropic failure criterion for geomaterials [J].International Journal of Solids and Structures,2010,47(22/23):3166- 3185.

[8] PIETRUSZCZAK S,MROZ Z.Formulation of anisotropic failure criteria incorporating a microstructure tensor [J].Computer and Geotechnics,2000,26(2):105- 112.

[9] PIETRUSZCZAK S,MROZ Z.On failure criteria for anisotropic cohesive-frictional materials [J].International Journal for Numerical and Analytical Methods in Geomechanics,2001,25(5):509- 524.

[10] 余天堂,卢应发,SHAO J F,等.沉积岩的一种各向异性模型 [J].岩土力学,2002,23(1):47- 50. YU Tian-tang,LU Ying-fa,SHAO J F,et al.An anisotropic model of sedimentary rocks [J].Journal of Geotechnical Mechanics,2002,23(1):47- 50.

[11] 余天堂.岩土材料固有各向异性的模拟 [J].岩石力学与工程学报,2004,23(10):1604- 1607. YU Tian-tang.Modeling of inherent anisotropy for geotechnical material [J].Chinese Journal of Rock Mechanics and Engineering,2004,23(10):1604- 1607.

[12] ZHONG S Y,XU W Y,LING D S.Influence of the parameters in the Pietruszczak-Mroz anisotropic failure criterion [J].International Journal of Rock Mechanics and Mining Sciences,2011,48(6):1034- 1037.

[13] LADE P V.Modeling failure in cross-anisotropic frictional materials [J].International Journal of Solids and Structures,2007,44(16):5146- 5162.

[14] LADE P V.Failure criterion for cross-anisotropic soils [J].Journal of Geotechnical and Geoenvironmental Engineering,2008,134(1):117- 124.

[15] LADE P V.Three-dimensional failure in geomaterials:experimentation and modeling [M]∥Constitutive Modeling of Geomaterials.[S.l.]:Springer Berlin Heidelberg,2013:47- 58.

[16] CHU X H,CHANG J F,JIANG Q H,et al.Numerical simulation of progressive failure in transversely isotropic geomaterials[C]∥Advance in Heterogeneous Material Mechanics.Lancaster:Destech Publication Inc.,2011:965- 968.

[17] DE BORST R.Simulation of strain localization:a reappraisal of the Cosserat continuum [J].Engineering Computations,1991,8(4):317- 332.

[18] LI X K,TANG H X.A consistent return mapping algorithm for pressure-dependent elastoplastic Cosserat continua and modeling of strain localization [J].Computers & Structures,2005,83(1):1- 10.

[19] 余村,楚锡华,唐洪祥,等.基于Cosserat连续体的颗粒破碎影响研究 [J].岩土力学,2013,34(增刊1):67- 79. YU Cun,CHU Xi-hua,TANG Hong-xiang,et al.Study of effect of particle breakage based on Cosserat continuum [J].Journal of Geotechnical Mechanics,2013,34(Sup 1):67- 79.

[20] ARSLAN H,STURE S.Finite element analysis of localization and micro-macro structure relation in granular materials(Part I):Formulation [J].Acta Mechanica,2008,197(3/4):135- 152.

Finite Element Simulation of Strain Localization in Transversely Isotropic Geomaterials

CHANGJiang-fang1，2XUYuan-jie1CHUXi-hua1

(1.Engineering Mechanics Department,Wuhan University,Wuhan 430072,Hubei,China; 2. Mechanics Engineering Department,Shijiazhuang Tiedao University,Shijiazhuang 050043,Hebei,China)

The anisotropic properties of geomaterials are significantly related to their inherent microstructures. In this paper,a modified Drucker-Prager yield criterion for transversely isotropic materials is developed by evaluating the internal friction angle with the stress state,the microstructure tensor and the material principal direction.Then,based on the Cosserat continuum theory,a consistent return mapping algorithm for the modified criterion is formulated,and a consistent tangent modulus matrix is achieved.Moreover,the codes are implemented through the user defined element subroutine(UEL) in the finite element software Abaqus,and the correctness of the program is verified by comparing the theoretical results with the relationships of the material strength to the principal direction and anisotropic degree of the material in the integration points.Finally,the influences of the principal direction and anisotropic degree of the material on the bearing capacity and the failure mode of the structure are emphatically analyzed by numerical examples,which are then compared with the results based on the classical continuum theory.It is found that the above-mentioned method is effective in simulating the strain localization of transversely isotropic geomaterials.

geomaterials;geomechanics;transverse isotropy;Cosserat continuum;yield criterion; strain localization

2015- 01- 19

国家自然科学基金资助项目(11172216)；国家重点基础研究发展计划项目(2010CB731502)；湖北省自然科学基金资助项目(2013CFB287)；河北省杰出青年科学基金资助项目(E2015210040) Foundation items: Supported by the National Natural Science Foundation of China(11172216),the National Program on Key Basic Research Project of China(2010CB731502)and the Natural Science Foundation of Hubei Province(2013CFB287)

常江芳(1988-)，女，博士，讲师，主要从事岩土材料强度与破坏的数值研究.E-mail:cjf881024@163.com

† 通信作者: 徐远杰(1956-)，男，博士，教授，主要从事工程结构破坏数值仿真研究.E-mail:xyj9781@163.com

1000- 565X(2016)10- 0070- 11

O 34

10.3969/j.issn.1000-565X.2016.10.011