液氮冻结食品冻结时间的计算方法及实验验证

周小清柳建华，2徐小进梁亚英

（1上海理工大学能源与动力工程学院 上海 200093；2上海市动力工程多相流动与传热重点实验室 上海 200093；3中国船舶重工集团公司第七○四研究所 上海 200031）

液氮冻结食品冻结时间的计算方法及实验验证

周小清1柳建华1，2徐小进3梁亚英1

（1上海理工大学能源与动力工程学院 上海 200093；2上海市动力工程多相流动与传热重点实验室 上海 200093；3中国船舶重工集团公司第七○四研究所 上海 200031）

冻结时间是评价冻结食品质量的重要指标，正确计算冻结时间是食品冻结装置优化设计及运行的关键。本文通过建立液氮速冻实验平台，测试了食品的冻结时间，介绍了现有的理论模型，选择了几种典型的计算方法应用于食品冻结，并将各模型的理论结果与实验值进行比较，分析各偏差原因，获得计算食品冻结时间最准确的方法。以有限长圆柱状食品为例，通过研究发现在整个氮气温度场中国际制冷学会模型计算结果与实验值最相近，平均偏差为8.86%，分段计算法次之，平均偏差小于15%。

冻结食品；冻结时间；计算模型；实验研究

随着社会的进步，人们对食品品质的要求越来越高，与冻结速率有限的传统速冻装置相比，液氮速冻技术（可实现超低温冻结）成为近年来的研究热点［1］。作为评价食品冻结质量的主要指标，冻结时间是合理设计冻结装置的重要依据［2-3］。因此，能准确计算和预测冻结时间，对液氮速冻装置与液氮速冻加工工艺的设计意义重大［4］。

自1913年德国学者普朗克（Plank）提出食品冻结时间计算式以来，对冻结时间的研究一直持续［5-9］。从文献来看，食品冻结时间的确定主要有三种方法：经验公式预测、数值计算预测和实验测定法［10-11］。经验公式方法的特点是简单易得、方便快捷，综合实验与理论两种方法形成公式，误差相对较大。数值计算方法通过理论分析和计算机建模进行计算和预测，计算过程更为复杂，但是预测结果准确。实验测定法精度高、可靠性好，但工作量大，周期长，在实际应用中常受到客观条件的限制。

本文研究了液氮冻结食品的冻结时间，对现有的理论计算模型作一介绍，选择几种典型的经验公式计算方法应用于食品冻结。并搭建不同温度段氮气冻结食品的实验台，对冻结时间进行测试。将各计算式的结果与实验值进行比较，分析各偏差原因，获得计算食品冻结时间较准确的方法，为液氮速冻的进一步研究提供理论依据。

1 计算方法

1941年，普朗克在一些不完全符合实际的假设的情况下，推导出迄今仍公认并引用的计算食品冻结时间的基础方程。后人在其基础上不断改进和修正，提出了很多新的计算公式，本文列举几个较为常用的公式。

1.1 国际制冷学会模型

在对Plank模型的修正上，国际制冷学会［12］考虑了冻结段和深冷段，引入了比焓差以代替Plank模型中的冻结潜热L：

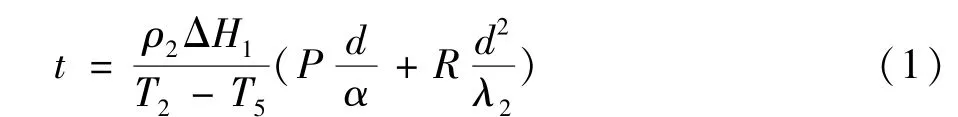
式中：t为冻结时间；ΔH1为食品的熔化潜热以及食品中心初始温度和冻结终温之间的显热之和，ΔH1=L1+c2（T2-T6），J／kg，其中L1为食品的熔化潜热，J／kg；T6为食品中心的冻结最终温度，℃；ρ2为食品冻结后的密度，kg／m3；T2为食品的初始冻结温度，℃；T5为冷却介质的温度，℃；d为食品的特征尺寸（无限大平板的厚度、圆柱或球体的直径或长方体的最小尺度），m；α为食品的表面对流换热系数，W／（m2·K）；P，R为食品的几何形状参数；λ2为冻结层的热导率，W／（m·K）。

1.2 Cleland和Earle模型

1979年Cleland A C等［13-14］考虑显热量对冻结时间的影响，提出了通用性强的普朗克无量纲修正式。1982年，Cleland A C等［15］简化了其早期的模型，考虑了食品的形状，引入了形状尺寸 （EHTD）1，冻结时间计算式如下：

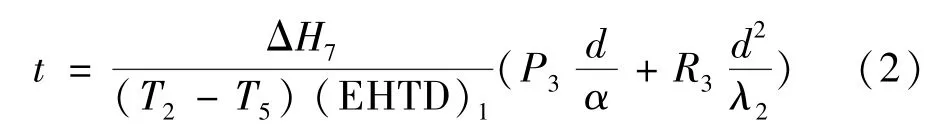
式中：Δ H7为食品初始冻结温度和食品中心冻结终点温度之间的焓差，J／kg；P3，R3为Plank几何参数的修正值，分别由以下二式得到，

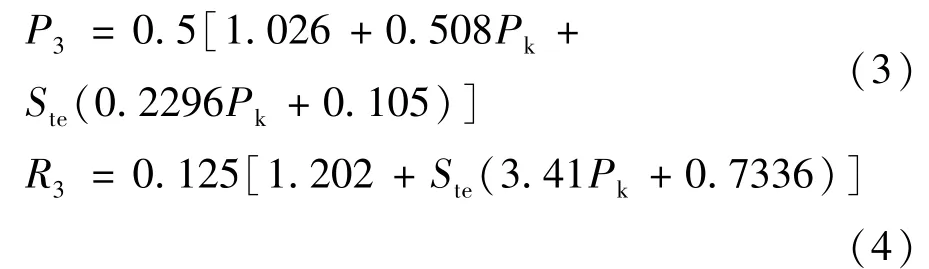
式中：Pk是由Cleland和Earle定义的普朗克数，反映初始冻结温度以上显热量对冻结时间的影响，；c1为食品未冻结时的比热容，J／（kg·℃）；T1为食品初始温度，℃；L为食品冻结潜热，J／（kg·℃）；Ste是由Cleland和Earle定义的斯蒂芬数；Bi是由Cleland和Earle定义的毕渥数，Bi=；（EHTD）1为食品的形状尺寸，无限大平板（EHTD）1=1；无限长圆柱（EHTD）1=2；球体（EHTD）1=3；有限长圆柱（EHTD）1由以下公式计算：

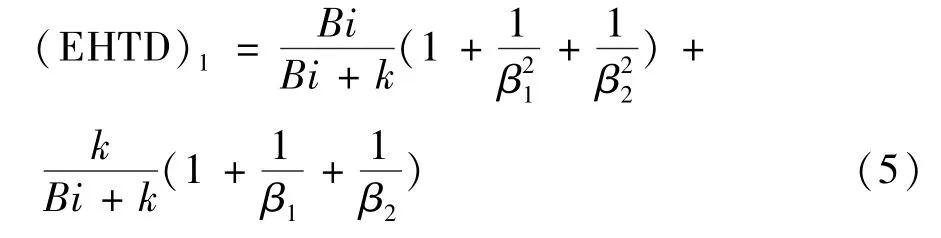
1984年，Cleland A C等［16］提出了新的普朗克修正式，此式在之前的基础上又包含了冻结过程相变温度下降对冻结时间的影响。

式中：ΔH8为食品从初始冻结温度T2降至-10℃时的比焓差值，J／kg。

此模型的使用条件是：0.2＜Bi＜20，0＜Pk＜0.55，0.15＜Ste＜0.35。

1.3 分段计算模型

食品冻结全过程可划分为冻结前降温（预冷）、冻结、冻结后降温（深冷）三个阶段：食品由初始温度T1降至冰点T2，食品由开始冻结温度T2降至食品中心达到冻结点T2，食品由中心冰点T2降低至最终温度T6。通过计算各阶段时间，相加后得到总的冻结时间。

针对这种模型，De Michelis A等［17］提出针对矩形块状和有限长圆柱状食品的冻结时间公式：

式中：预冷时间和深冷阶段的时间 tp和tr按Carslaw H S等［18］提出的方法计算。

结冰段时间tce按以下公式计算：

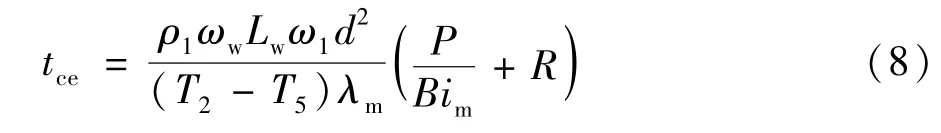
式中：ρ1为食品冻结前的密度，kg／m3；ωw为食品中（未冻结）水分的质量分数，%；Lw为纯水的潜热，335×103J／kg；ω1为食品的结冰量，ω1=，g；λm为Tc时的热导率，W／（m·K）。

1.4 几何因子预测法

虽然Plank给出的计算食品冻结时间的公式不够准确，但在理论上给人以启迪：对于各种形状的食品，其它参数相同时，冻结时间必然存在一个比例关系。Cleland A C［19］因此提出了等效传热因子 E（Equivalent Heat Transfer Dimensions）的概念。因此任何形状食品的冻结时间可由具有相同特征尺寸的无限大平板的冻结时间和形状因子E［20］表示：

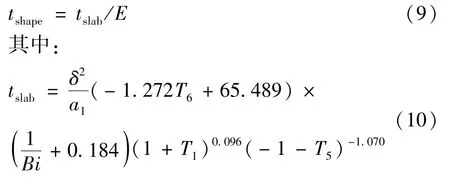
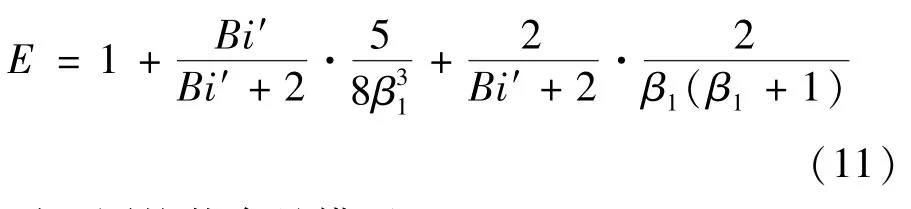
对于圆柱状食品模型：

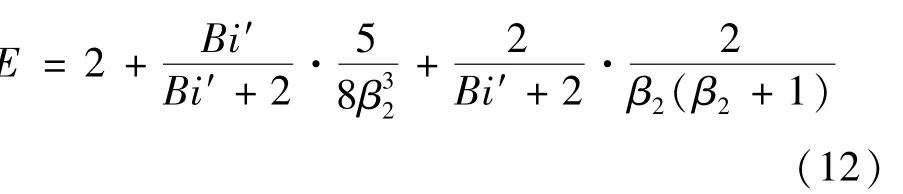
式中：β1为矩形长边和短边长度之比；β2为长径比（长度与直径的比值），

2 实验研究

2.1 研究对象

实验选择价格低廉又普遍食用的马铃薯，便于制作简单形状的样品，且有利于进行温度测量和传热分析。选取有限长圆柱状马铃薯，长4 cm、直径2 cm，初始温度为18℃，冻结点为-1.8℃，冻结终温为-18℃。冻结实验氮气温度段为-170～-50℃之间每-20℃间距的7个温区。

2.2 实验装置

图1为实验装置示意图，实验装置由测温系统、液氮罐和支架三大部分组成。其中测温系统包括铜-康铜热电偶、安捷伦（Agilent34970A）采集仪以及用VB（Visual Basic）编制的测温程序。在食品中心处布置热电偶测量其中心温度，此外，为了查看其周围的氮气温度在食品表面之外布置另一测点，以验证食品是否处于设定的氮气下冻结，测点位置在距离食品表面0.2 cm左右处。

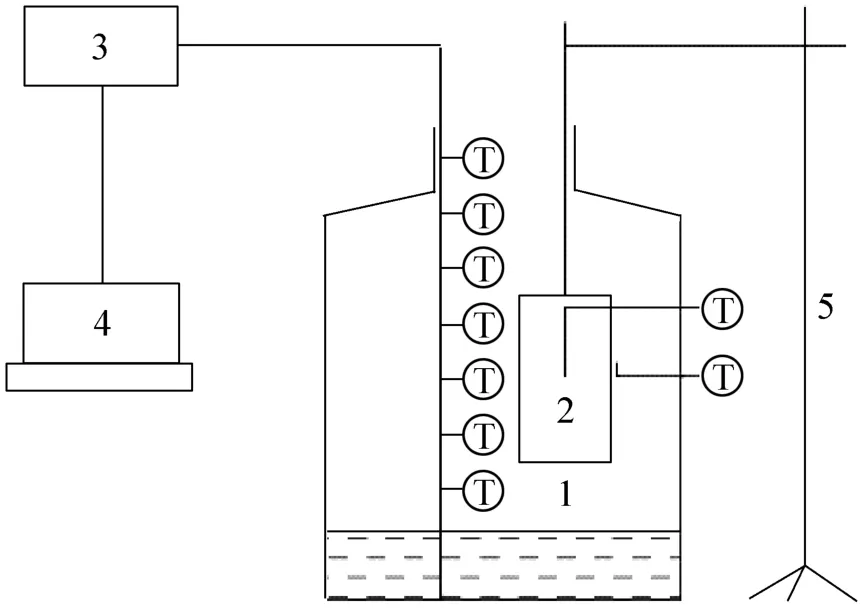
图1 液氮冻结马铃薯实验装置Fig.1 The experiment device of liquid nitrogen freezing

图2 实验流程图Fig.2 The flow chart of the experiment

2.3 实验步骤

图2给出了液氮冻结马铃薯实验测温过程的流程，当充氮结束，敞口罐内液氮汽化一段时间后，开始测量其内的氮气温度场。打开安捷伦采集仪，开启计算机温度采集界面，将布置好测点的竹竿缓慢放入罐中，观察各通道数据的变化并至稳定。通过测量及计算确定杜瓦瓶中各温度氮气的位置，将事先固定在一细竹竿上的食品样品放于某一高度的氮气中降温，当马铃薯中心温值冻结至-18℃时，取出食品完成此温度下食品的冻结实验。类似地，将食品一一放入其它温区，实现样品相应的降温操作，完成其余阶段的冻结实验。各阶段的氮气冻结马铃薯完成后，关闭测温系统，整个冻结实验结束。

3 结果分析

在确立各计算参数后，得到食品在国际制冷学会模型、Cleland＆Earle模型、分段计算模型以及几何因子预测法计算的四种算法下的理论冻结时间。通过与实验值作比较得出如表1、表2的结果，绘制在不同温度下冻结食品所对应的冻结时间趋势变化图，如图3所示。

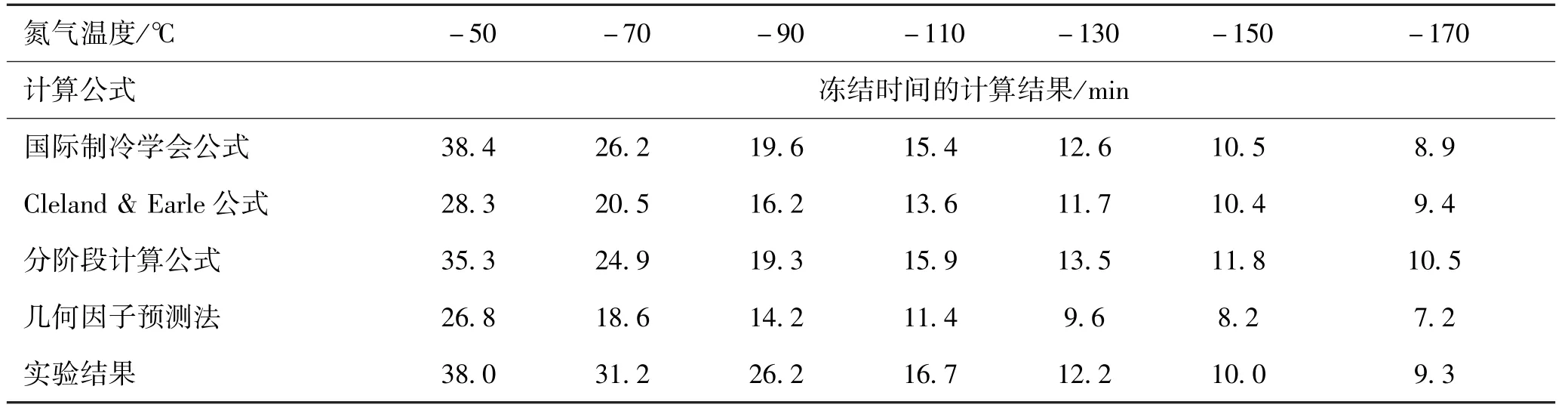
表1 冻结时间的实验结果与计算值的对比Tab.1 Com parison of the experimental data and calculated value on freezing time

表2 计算值与实验结果的偏差Tab.2 The deviation between the calculated value and experimental results

结合表1、表2及图3发现，将食品放置在-170 ～-50℃的氮气中冻结，国际制冷学会模型计算的冻结时间值在整个温度段与实验结果最接近，平均偏差仅达8.86%。

图3（b）给出了Cleland＆Earle计算式与实验值的比较图形，二者平均偏差在20%之内。由偏差曲线可知，在相对高温的氮气温区，偏差稍大，表明该模型在整个氮气场中，更适合用于相对低温氮气的理论计算。

图3（c）给出了Michelis和Calvelo提出的分段计算法，不仅物理意义更加明确，且理论计算接近实际时间，在整个氮气场中的平均偏差在15%之内。

图3（d）可以看出Cleland的几何因子预测法的计算结果与实际测得结果的平均偏差相对于前面三者略微升高，达到30%。且在-90～-50℃的氮气温区相差较大，说明此模型在液氮汽化的低温氮气冻结食品上的应用存在区域性。

4 结论

本文搭建了液氮冻结食品的实验台，利用液氮汽化的低温氮气冻结食品，将有限长圆柱状马铃薯在-170～-50℃的液氮环境中从18℃冻结至-18℃，测得相应的冻结时间。将冻结时间的实验值与四种经典计算模型的理论值相比较，得出如下结论：

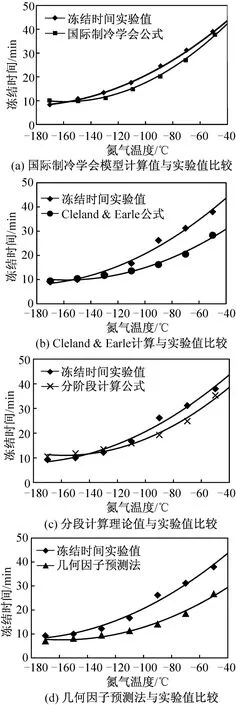
图3 各计算值与实验值的对比图Fig.3 Comparison of the calculated value and experimental value

1）国际制冷学会模型更适合于各个氮气温度区的冻结计算，平均偏差仅8.86%，分段计算法次之，平均偏差在15%之内。

2）Cleland＆Earle模型和几何因子预测法在整个氮气场中存在区域性，Cleland＆Earle模型更适合用于相对低温氮气的理论计算。几何因子预测法与实验结果的整体偏差较大，相对而言其在较低温度下的偏差更小。

本文受上海市科委项目（13DZ2260900）资助。（The project was supported by Shanghai Municipal Science and Technology Commission Funded Project（No.13DZ2260900）.）

［1］ 郭旭峰，陶乐仁，华泽钊，等.液氮速冻装置中液氮耗量与冷冻能力的分析［J］.低温与特气，2002，20（5）：8-11.（GUO Xufeng，TAO Leren，HUA Zezhao，et al.Analysis of LN2（Liquid Nitrogen）consumption and freezing capacity on LN2freezer［J］.Low Temperature and Special Gas，2002，20（5）：8-11.）

［2］ Cleland A C，Özilgen S.Thermal design calculations for food freezing equipment—past，present and future：calculs thermiques pour la conception de congélateurs industriels：le passé，le présent et le futur［J］.International Journal of Refrigeration，1998，21（5）：359-371.

［3］ Campañone L A，Salvadori V O，Mascheroni R H.Food freezing with simultaneous surface dehydration：approximate prediction of freezing time［J］.International Journal of Heat and Mass Transfer，2005，48（6）：1205-1213.

［4］ 李杰，谢晶，张珍.食品冻结时间预测方法的研究分析［J］.安徽农业科学，2008，36（23）：10178-10181.（LI Jie，XIE Jing，ZHANG Zhen.Analysis of forecasting methodology of freezing time in food［J］.Journal of Anhui Agricultural Sciences，2008，36（23）：10178-10181.）

［5］ 赖建波，臧润清，车晶.有限长圆柱状食品冻结时间的计算方法及实验验证［J］.制冷学报，2004，25（1）：6-9. （LAI Jianbo，ZANG Runqing，CHE Jing.Calculating method and experimental verifying on freezing time of finite cyclical foodstuff［J］.Journal of Refrigeration，2004，25 （1）：6-9.）

［6］ 屠建祥，刘宝林，陶乐仁，等.速冻过程中食品冻结速度的数值计算［J］.低温工程，2000（2）：44-48.（TU Jianxiang，LIU Baolin，Tao Leren，et al.Numerical method of freezing rate during food quick freezing［J］.Cryogenics，2000（2）：44-48.）

［7］ 关志强，戴午子，叶彪，等.食品冻结时间的数值计算［J］.制冷学报，1994，15（4）：33-35.（GUAN Zhiqiang，DAI Wuzi，YE Biao，et al.Numerical prediction of freezing time of foods［J］.Journal of Refrigeration，1994，15（4）：33-35.）

［8］ Delgado A E，Sun D W.Heat and mass transfer models for predicting freezing processes-a review［J］.Journal of Food Engineering，2001，47（3）：157-174.

［9］ Pham Q T.Simplified equation for predicting the freezing time of foodstuffs［J］.International Journal of Food Science ＆Technology，1986，21（5）：209-219.

［10］曲春民，孙勇，陈忠海，等.鲜食玉米冻结过程传热分析及冻结时间的研究［J］.制冷学报，2006，27（6）：34-38. （QU Chunmin，SUN Yong，CHEN Zhonghai，et al.Research on heat transfer process of the quick freezing of the fresh unripe maize and freezing time［J］.Journal of Refrigeration，2006，27（6）：34-38.）

［11］张中秀，赵兰萍.简单形状食品冻结时间计算方法的分析研究［J］.冷饮与速冻食品工业，2006，12（2）：9-12. （ZHANG Zhongxiu，ZHAO Lanping.Analysis and research on freezing time calculating for simple shaped foodstuff［J］.Beverage＆Fast Frozen Food Industry，2006，12 （2）：9-12.）

［12］Refrigeration I I O.Recommendations for the processing and handling of frozen foods［J］.International Institute of Refrigeration，1986.

［13］Cleland A C，Earle R L.A comparison of freezing calculations including modification to take into account initial superheat［J］.Suppl Bull Iif／iir Int Inst Refrig，1976.

［14］Cleland A C，Earle R L.A comparison of methods for predicting the freezing times of cylindrical and spherical foodstuffs［J］.Journal of Food Science，1979，44（4）：958-963.

［15］Cleland A C，Earle R L.Assessment of freezing time prediction methods［J］.Journal of Food Science，1982，49：1035.

［16］Cleland A C，Earle R L.Freezing time predictions for different final product temperatures［J］.Journal of Food Science，1984，49（4）：1230-1232.

［17］De Michelis A，Calvelo A.Freezing time predictions for brick and cylindrical shape foods［J］.Journal of Food Science，1983，48（3）：909-913.

［18］Carslaw H S，Jaeger J C.Conduction of heat in solids ［M］.Oxford：Clarendon Press，1959.

［19］Cleland A C，Earle R L.Freezing time prediction for foods —a simplified procedure［J］.International Journal of Refrigeration，1982，5（3）：134-140.

［20］Salvadori V O，Mascheroni R H，De Michelis A.Freezing of strawberry pulp in large containers：experimental determination and prediction of freezing times［J］.International Journal of Refrigeration，1996，19（2）：87-94.

About the author

Zhou Xiaoqing，female，master candidate，College of Energy and Power Engineering，University of Shanghai for Science and Technology，+86 18801732865，E-mail：791259088＠qq.com.Research fields：refrigeration and cryogenic technology.

Calculating Method and Experimental Verification of Freezing Time of Frozen Food by Liquid Nitrogen

Zhou Xiaoqing1Liu Jianhua1，2Xu Xiaojin3Liang Yaying1

（1.School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai，200093，China；2.Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering，Shanghai，200093，China；3.No.704 Research Institute，CSIC，Shanghai，200031，China）

Freezing time is an important index to evaluate the quality of frozen food，and the correct calculation of freezing time is the key to the optimal design and operation of food freezing equipment.In this paper，the freezing time is tested by the established frozen experiment platform with liquid nitrogen.After introducing existing models，several typical calculation methods are chosen to calculate the food freezing time.By comparing the theoretical results with the experimental results，the most accurate method to calculate the food freezing time is obtained.Taking the finite cyclical foodstuff as an example，the result shows that the International Institute of Refrigeration Model has the smallest difference with the experimental results，and the average deviation is 8.86%，while the Staging Model takes second place with an average deviation less than 15%.

frozen food；freezing time；calculation model；experimental study

TB64；TS205.7

：A

0253-4339（2016）06-0113-06

10.3969／j.issn.0253-4339.2016.06.113

周小清，女，硕士研究生，上海理工大学能源与动力工程学院，18801732865，E-mail：791259088＠qq.com。研究方向：制冷及低温工程。

国家自然科学基金（51176129）资助项目。（The project was supported by the National Natural Science Foundation of China（No. 51176129）.）

2016年3月8日