重型运载火箭轨迹/总体参数一体化优化方法

孙乐园, 贾如岩, 杨枝山, 江振宇

(国防科学技术大学 航天科学与工程学院, 湖南 长沙 410073)

重型运载火箭轨迹/总体参数一体化优化方法

孙乐园, 贾如岩, 杨枝山, 江振宇

(国防科学技术大学 航天科学与工程学院, 湖南 长沙 410073)

研究了重型运载火箭轨迹/总体参数一体化优化问题。建立了一体化参数优化模型,设计了一种双环迭代优化算法,外环采用遗传算法进行参数优化,内环通过带自适应松弛因子的改进牛顿迭代法进行参数迭代。针对牛顿迭代法对模型本身及迭代初值敏感的问题,提出了一种模型变量筛选方法和迭代初值生成方法。基于Morris参数全局灵敏度分析法筛选出对终端等式约束影响最大的参数作为牛顿迭代变量,以历史迭代收敛值作为当前迭代初值。并通过迭代误差监控,保证了算法的鲁棒性。以三级液体重型运载火箭为对象,进行了一体化优化仿真。仿真结果显示起飞总质量减少了4.09%,表明设计的双环迭代优化算法能在复杂约束下完成重型运载火箭轨迹/总体参数一体化优化。

重型运载火箭;一体化优化;改进牛顿迭代法;全局灵敏度分析;迭代初值

随着人类空间探索的不断深入,世界各国已经将越来越多的探索目标瞄准了更加遥远的深空[1]。在我国“载人航天工程”和“探月工程”顺利实施的基础上,为了满足未来载人登月、深空探测以及建设大型空间设施等重大航天任务的需求,发展具备大吨位运载能力的重型运载火箭成为我国航天技术发展的重要支柱[2]。重型运载火箭的总体优化设计工作是其研制阶段的牵引项目。在概念设计阶段,总体参数和轨迹参数的一体化优化设计可以最大程度挖掘运载火箭设计性能[3]。一体化优化设计的关键在于设计变量和目标函数选择,以及各学科参数间的耦合问题[4]。国内外学者基于这些问题做了大量研究工作,并成功应用于工程实际中[5-7]。

遗传算法以解的多样性和并行性优势,较好地避免了陷入局部最优解的问题,成为目前在运载火箭一体化优化领域应用最为广泛的智能优化方法[8-9]。但是传统的智能优化算法虽然能较好地解决约束上下限的问题,但处理等式约束问题效率不高,而运载火箭一体化优化问题中通常包含多个等式约束。牛顿迭代法求解等式约束问题具有收敛快、稳定性好、精度高等优点,可通过牛顿迭代法对优化过程中的等式约束进行迭代求解[10]。但是牛顿迭代法对模型变量和迭代初值敏感,运载火箭一体化优化问题设计变量多,变化范围大,会导致牛顿迭代法难以收敛。

本文研究了重型液体运载火箭轨迹/总体参数一体化优化设计问题。通过设计一种基于遗传算法和牛顿迭代法的双环迭代优化算法实现参数的一体化优化。针对牛顿迭代法对模型及迭代初值敏感的问题,采用Morris参数全局灵敏度分析法[11]筛选出敏感变量作为迭代变量,保证牛顿迭代法快速收敛,以初值继承方法提供迭代初值,克服不合理初值导致迭代过程发散的问题。并通过误差监控保证算法鲁棒性。

1 优化数学模型

1.1 质量计算模型

本文针对具体对象,将重型运载火箭质量分为固定质量和变化质量。推进剂加注量是液体运载火箭的主要变化质量,而贮箱质量也会随着推进剂量发生改变。本文采用椭球封头的圆柱形贮箱,当火箭直径保持不变时,贮箱封头质量恒定,仅贮箱柱段质量发生变化,柱段质量可表示为推进剂质量的函数

(1)

式中,mft为贮箱封头内的推进剂质量,D、d分别为贮箱的外径和内径,ρz为贮箱材料密度,ρp为推进剂密度,推进剂总质量mp为设计变量。

设备质量、发动机质量和级间段质量的变化量相对于重型运载火箭总质量为小量,将三者视为固定质量。

可得液体运载火箭起飞质量计算模型

m0=mg+mp+mzp

mzp=f(mp)

(2)

式中，mg为固定质量,推进剂质量mp考虑起飞前消耗和关机剩余量。

1.2 发动机性能计算模型

运载火箭飞行性能主要受发动机推力Pe和工作时间tgz影响,两者与推进剂质量的关系可表示为

(3)

式中，比冲Isp由推进剂种类决定。Pe、mp、tgz中仅2个独立变量。发动机推力大小取工作时间内的平均值,作为设计变。

1.3 飞行程序控制模型

飞行程序控制模型采用垂直起飞和程序转弯,俯仰程序角设计如下:

1) 一级飞行段

运载火箭一级在稠密大气层中飞行,由于受到飞行性能约束,飞行程序通常采用固体的形式[12]

(4)

攻角转弯段

α(t)=-αm·sin2f(t)

(5)

式中

(6)

(7)

αm为最大转弯负攻角,为待设计参数。tb为攻角转弯开始时间,te为攻角转弯结束时间,tm为最大负攻角时间,t1为一级关机时间。

2) 二、三级飞行段

二、三级飞行段大气已相当稀薄,气动载荷对弹道已没有特殊要求,采用程序俯仰角离散化形式

i=1,2 (8)

1.4 弹道计算模型

弹道计算模型考虑以下基本假设:

1) 地球为两轴旋转均值椭球;

2) 采用考虑J2项的近似引力模型;

3) 箭体无惯性,完全按程序飞行

4) 不考虑外界因素对发动机推力和流量的影响,不考虑发动机过度特性;

采用发射系中的空间弹道计算方程,详细计算模型参考文献[12]。

2 轨迹/总体参数一体化优化问题

2.1 目标函数

运载火箭起飞质量是一项重要性能指标,影响着其成本及维护使用性能。在给定运载能力的前提下,以起飞质量最小为优化目标函数,即

minJ=m0

(9)

2.2 优化设计变量

运载火箭总体性能主要由各级推进剂加注量及推力大小决定,同时受飞行程序影响,选择以下参数为轨迹/总体参数一体化设计变量

(10)

分别为三级推进剂量、三级推力、第一级转弯最大负攻角、第三级俯仰角变化率和有效载荷质量。

2.3 约束条件

约束条件主要包括过程约束和终端约束。

根据工程实际需求,选择如下指标作为过程约束条件:

1) 火箭起飞推重比:N0min≤N0(X)≤N0max;

2) 最大法向过载:ny(X)≤nymax;

3) 最大动压:q(X)≤qmax.

终端约束由目标轨道决定。对于圆轨道,终端绝对状态约束为

对于运载能力给定的情况,需要设置有效载荷质量约束:mu≥mu-need,mu-need为任务要求的有效载荷质量。

3 参数优化方法

3.1 双环迭代优化方法

基于以上建模,将运载火箭轨迹/总体参数一体化优化问题转化为一个带有复杂不等式约束和等式约束的多参数优化问题。采用外环遗传算法优化,内环改进牛顿法迭代的双环迭代优化方法对优化问题求解。针对牛顿迭代法收敛过程对模型本身及迭代初值敏感的问题,首先基于Morris法对所有设计变量进行全局灵敏度分析,筛选出对终端等式约束影响最为显著的3个设计变量作为牛顿迭代变量,影响较小的作为遗传算法优化变量。由于等式约束对遗传算法个体参数敏感度较低,对于不同个体,迭代参数收敛值不会相差太远,因此采用初值继承方法,以上一个体的迭代参数收敛值作为当前遗传个体下迭代参数的初值,从而避免初值不合理引起的迭代发散问题。并通过误差监控,保证优化算法的鲁棒性。算法流程图见图1。

图1 算法流程图

根据上述算法流程图,算法关键步骤为:

1) 设计变量灵敏度分析

基于Morris法对设计变量X=(x1,x2,…,x9)各元素(均为归一化变量)进行灵敏度分析,灵敏度最大的3个元素构成的设计变量XN=(x(1),x(2),x(3))作为内环牛顿迭代变量,其余6个元素构成外环遗传算法优化变量XG=(x(4),…,x(i),…x(9))。

2) 种群初始化

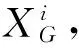
3) 牛顿迭代计算

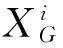
c) 对迭代过程的终端状态误差进行监控,当迭代误差发散时,放弃本次迭代,以牛顿迭代初值作为迭代环输出,并令误差标识量esp=∞(实际应用时取一个充分大的正实数),防止无法满足入轨状态的遗传个体成为最优解。

4) 适应值计算

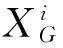
3.2 遗传算法适应值函数

运载火箭参数优化问题是一个带多个不等式约束的非线性规划问题,通过在遗传算法适应值函数中增加惩罚项来处理不等式约束下的优化问题。本文中取加法形式的惩罚函数,构造适应值函数为

Eval(X)=m0(X)+p(X)+pesp(esp)

(11)

式中约束惩罚项p(X)由下式确定

(12)

式中，ζi为第i个约束的惩罚系数,m为不等式约束个数。

迭代误差惩罚项

pesp(esp)=esp

(13)

3.3 改进牛顿迭代法

运载火箭轨迹/总体参数一体化优化问题是一个带有等式约束的多参数优化问题。针对圆轨道的入轨需求,本文给出了3个终端等式约束,而简单遗传算法只能解决约束上下限的优化问题,对等式约束问题往往转化为2个不等式约束进行处理,效率较低。而牛顿迭代法求解等式约束问题具有收敛快、精度高的优点。本文通过设计一个三维变量x=(x(1),x(2),x(2))T,(x(1),x(2),x(2)∈X),将等式约束优化问题转化为求解三元非线性方程组的问题,并采用改进牛顿迭代法[13]进行求解

(14)

以x0为初始猜测值,牛顿法第j步迭代公式为

xj=xj-1+dj, j=1,2,…

(15)

搜索方向由(16)式确定

(16)

当初始点离最优解较远,牛顿法迭代法不能保证搜索方向为最速下降方向[14],为了克服这一问题,改进牛顿迭代法选取牛顿方向d作为搜索方向,而用一维搜索确定最优步长,采用自适应松弛因子

(17)

第j步采用迭代公式为

xj=xj-1+σjdj, j=1,2,…

(18)

3.4 基于Morris法的参数全局灵敏度分析

为了保证牛顿迭代法快速收敛,要求迭代设计变量x与终端等式约束紧密相关。本文基于Morris法对所有设计变量进行全局灵敏度分析,筛选出对终端状态影响最大的3个变量作为牛顿迭代变量。

Morris法由Morris在1991年提出,能以较小的计算代价得到参数全局灵敏度的比较及参数相关性和非线性的定性描述。Morris法的基本思想是[15]:假定衡量参数xi灵敏性的“基本因素(EE)”服从某种分布均值为μi,标准差为σi的分布Fi,参数xi所对应的均值越大,则对模型输出的影响程度就越大,而标准差表示参数之间的相互作用程度。

设系统模型为y=y(x1,…,xi,…xm),根据Morris法进行模型参数全局灵敏度分析的基本算法流程为:

1) 令m维对角矩阵D每个对角元素等概率取为+1或-1,矩阵B∈为一个元素为1的严格下三角阵,Jm+1,m是(m+1)×m维所有元素都为1的矩阵,取

J*=(2B-Jm+1,m)·D+Jm+1,m

(19)

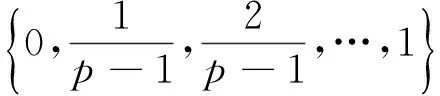
X=(x1,…,xi,…xm)

(20)

3) 设P为m×m维随机置换矩阵,即每行每列都只有一个值为1,其余为0。Jm+1,1为所有元素都为1的(m+1)×1维矩阵,则采样矩阵的随机化矩阵B*为

(21)

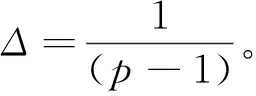
由于B*为随机取值,且相邻两行只有一列的元素不同,假设为第j列,即

(22)

式中，xj1-xj2=Δ。因此选择B(j)作为系统的输入参数向量,则第j个参数的基本因素(EE)可由下式计算

(23)

取所有m组相邻行作为模型输入参数向量,可获得m个参数的基本因素。

4) 进行N次采样,重复步骤1)到3),获得每个参数的N个基本因素样本值。

5) 计算每个输入参数xi(i=1,2,…,m)基本因素的样本均值作为μi的估计值,并据此判断输入参数的全局灵敏性。

4 优化算例与分析

根据本文建立的运载火箭轨迹/总体参数一体化优化模型,研究三级液体运载火箭的一体化优化设计问题。运载能力要求将60t有效载荷送入轨道倾角为68°的200 km近地圆轨道。

起飞推重比约束为1.2≤N0≤1.4,法向过载约束ny≤0.05,动压约束q≤0.025 MPa。

遗传算法种群规模取20,最大进化代数取100。牛顿迭代法终端高度误差小于1 000 m,绝对速度误差小于5 m/s,当地绝对速度倾角误差小于0.05°。

4.1 参数灵敏度分析结果

本文优化设计变量为

(24)

利用Morris法对参数进行灵敏度分析,分析结果见图2～图4。

图2 终端高度的灵敏度 图3 终端绝对速度的灵敏度图4 终端当地速度倾角的灵敏度

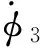
4.2 迭代优化结果与分析

基于参数灵敏度分析结果,对设计变量进行迭代优化。图5～图7为一个种群下基于初值继承方法的改进牛顿迭代法高度、速度、当地速度倾角的误差变化曲线(高度、速度为归一化标准量)。

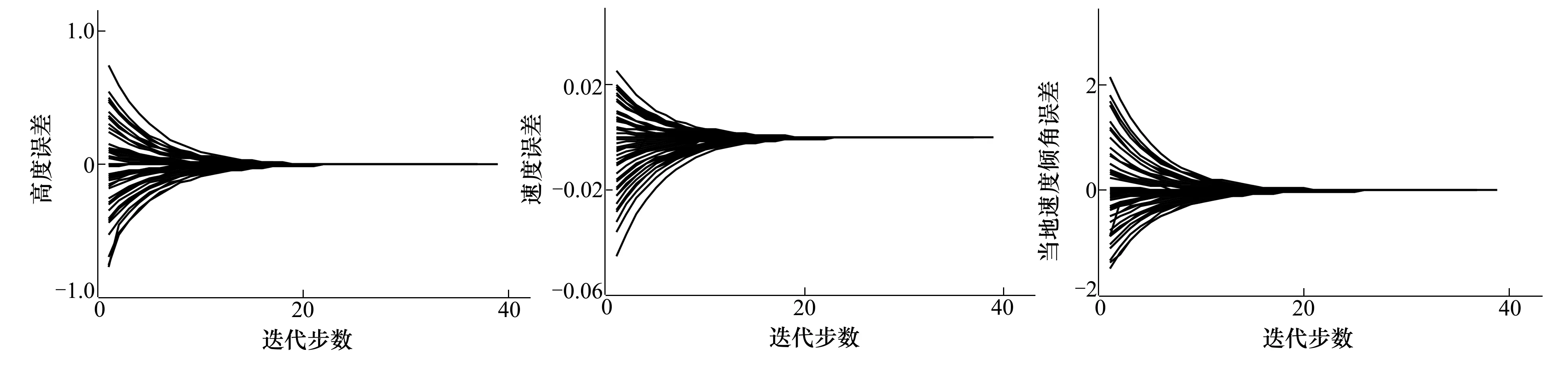
图5 高度误差收敛曲线 图6 速度误差收敛曲线图7 当地速度倾角误差收敛曲线

由图可知,初值继承方法较好解决了牛顿迭代法对初值敏感的问题,对每一个个体,迭代误差均能在25步以内收敛。

轨迹/总体参数优化结果如表1～表4所示。

表1 参数优化结果

表2 参数迭代结果

表3 不等式约束优化结果

表4 等式约束优化结果

优化计算结果表明,优化后起飞质量减轻了67 t(减少4.09%),相应的终端等式约束和过程不等式约束均得到很好满足。

5 结 论

运载火箭总体参数和轨迹参数优化设计是运载火箭总体优化设计的关键阶段。本文从工程实际出发,提出了一种运载火箭轨迹/总体参数一体化优化方法。

1) 建立了重型运载火箭轨迹/总体参数一体化优化问题的数学模型;

2) 设计了一种双环迭代优化算法,外环通过遗传算法对优化设计变量寻优,内环基于带自适应松弛因子的改进牛顿迭代法对迭代设计变量进行迭代求解。

3) 提出了一种基于Morris法的轨迹/总体参数全局灵敏度分析和初值继承的初值生成方法,较好解决了牛顿迭代法收敛过程对模型及初值敏感的问题,并通过迭代误差监控,保证了算法鲁棒性。

4) 优化结果表明,本文所提出的一体化优化算法能有效提高重型运载火箭整体设计性能,过程约束和终端约束均能很好满足,可为重型运载火箭轨迹/总体参数一体化优化设计工作提供参考。

[1] 马志滨, 何麟书. 国外重型运载火箭发展趋势述评[J]. 固体火箭技术, 2012, 35(1): 1-4 Ma Zhibin, He Linshu. Development Trend Review of Foreign Heavy-Lift Launch Vehicle[J]. Journal of Solid Rocket Technology, 2012, 35(1): 1-4 (in Chinese)

[2] 何巍, 刘伟, 龙乐豪. 重型运载火箭及其应用探讨[J]. 导弹与航天运载技术, 2011(1): 1-5 He Wei, Liu Wei, Long Lehao. Heavy Launch Vehicle and Its Application[J]. Missiles and Space Vehicles, 2011(1): 1-5 (in Chinese)

[3] 胡凡, 杨希祥, 江振宇, 等. 固体运载火箭轨迹/总体参数一体化优化设计研究[J]. 固体火箭技术. 2010, 33(6): 599-602 Hu Fan, Yang Xixiang, Jiang Zhenyu, et al. Integrated Optimization Design of Trajectory/System Parameters for Solid Launch Vehicle[J]. Journal of Solid Rocket Technology, 2010, 33(6): 599-602 (in Chinese)

[4] 肖飞, 向敏, 张为华. 多级固体运载火箭总体/弹道/轨道一体化设计与优化[J]. 空军工程大学学报, 2008, 9(5):19-13 Xiao Fei, Xiang Min, Zhang Weihua. Orbit Trajectory and System Integrated Design and Optimization of Multi-Stage Solid Rocket[J]. Journal of Air Force Engineering University, 2008, 9(5): 19-13 (in Chinese)

[5] 马加庆, 孙丕忠, 夏智勋, 等. 大型捆绑助推器总体/动力/轨道一体化设计与优化[J]. 国防科技大学学报, 2006, 28(1): 1-4 Ma Jiaqing, Sun Pizhong, Xia Zhixun, et al. Trajectory Solid Rocket and System Integration Design and Optimization on Rocket with Two Boosters[J]. Journal of National University of Defense Technology, 2006, 28(1): 1-4 (in Chinese)

[6] Anderson M, Burkhalter J, Jenkins R. Multi-Disciplinary Intelligent System Approach to Solid Rocket Motor Design Part I, Single and Dual Goal Optimization[R]. AIAA-2001-3599

[7] 罗亚中, 唐国金, 周黎妮, 等. 运载火箭性能计算一体化优化设计系统分析与设计[J]. 宇航学报, 2003, 24(3): 314-317 Luo Yazhong, Tang Guojin, Zhou Lini, et al. The Analysis and Design of Launch Vehicle Performance-Calculation Integrated Optimization Design System[J]. Journal of Astronautics, 2003, 24(3): 314-317 (in Chinese)

[8] 张宁宁, 闵昌万, 刘辉, 等. 临近空间直接入轨运载火箭级间比/弹道一体化优化设计[J]. 飞行力学, 2014, 32(3): 258-261 Zhang Ningning, Min Changwan, Liu Hui, et al. Integrated Optimization Design for Mass Distribution/Trajectory of Near Space Directly Injecting Carrier Rocket[J]. Flight Dynamics, 2014, 32(3): 258-261 (in Chinese)

[9] 徐玮, 孙丕忠, 夏智勋. 助推-滑翔导弹总体一体化优化设计[J]. 固体火箭技术, 2008, 32(4): 317-319 Xu Wei, Sun Pizhong, Xia Zhixun. Integrated Design and Optimization for Boost-Glider Missile[J]. Journal of Solid Rocket Technology, 2008, 32(4): 317-319 (in Chinese)

[10] 熊伟, 张耐民, 张艳玲. 基于组合算法的固体运载火箭快速运载能力优化[J]. 系统仿真学报, 2013, 25(11): 2552-2556 Xiong Wei, Zhang Naimin, Zhang Yanling. Quick Launch Ability Optimization for Solid Rocket Using Combinatorial Optimization Algorithm[J]. Journal of System Simulation, 2013, 25(11): 2552-2556 (in Chinese)

[11] Morris M D. Factorial Sampling Plans for Preliminary Computational Experiments[J]. Technometrics, 1991, 33: 161-174

[12] 陈克俊, 刘鲁华, 孟云鹤. 远程火箭飞行动力学与制导[M]. 北京:国防工业出版社, 2014 Chen Kejun, Liu Luhua, Meng Yunhe. Launch Vehicle Flight Dynamics and Guidance[M]. Beijing, National Defense Industry Press, 2014 (in Chinese)

[13] Lu P, Sun H, Tsai B. Closed-Loop Endo-Atmospheric Ascent Guidance[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(2): 283-294

[14] 何坚勇. 最优化方法[M]. 北京:清华大学出版社, 2014 He Jianyong. Optimization Method[M]. Beijing, Tsinghua University Press, 2014 (in Chinese)

[15] 贾如岩, 王涛, 江振宇, 等. 导弹尾罩分离运动不确定性分析[J]. 国防科技大学学报, 2014, 36(6): 88-92 Jia Ruyan, Wang Tao, Jiang Zhenyu, et al. Uncertainly Analysis of the Rocket Trail Cover Separation[J]. Journal of National University of Defense Technology, 2014, 36(6): 88-92 (in Chinese)

An Integrated Optimization Method of Trajectory/System Parameters for Heavy Launch Vehicles

Sun Leyuan, Jia Ruyan, Yang Zhishan, Jiang Zhenyu

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

The integrated optimization of trajectory/system parameters for heavy launch vehicles was investigated. A model of integrated optimization was set up. An iterative optimization algorithm with double loops was designed. The genetic algorithm was used to optimize parameters in outer loop, and the improved Newton iteration method with an adaptive relaxation factor was used to iterate parameters in inner loop. Aiming at the susceptibility of Newton iteration method to the model and initial values, a method of model variable screening and initial iteration values generation were proposed. Based on the Morris method of global sensitivity analysis, the parameters with the biggest influence on the terminal equality constraints were taken as the Newton iteration variables. And the historic convergent iteration values were set as the current initial iteration values. And the robustness of the algorithm was ensured by monitoring of the iterative error. A liquid heavy launch vehicle with 3 levels was set as an example for integrated optimization simulation. The results showed that initial mass decreases by 4.09% and demonstrate that the iterative optimization algorithm with double loops can complete the integrated optimization of trajectory/system parameters for heavy launch vehicles with complex constraints.

Heavy launch vehicles, Integrated optimization, Improved Newton iteration method, Global sensitivity analysis; Initial iteration values

2016-04-14

孙乐园(1991—)，国防科学技术大学硕士研究生，主要从事飞行器总体设计与系统仿真研究。

V421.1

A

1000-2758(2016)06-1101-07