基于加权模糊Petri网的无人机自主任务推理决策研究
2017-01-03谭雁英童明张艳宁祝小平
谭雁英, 童明, 张艳宁, 祝小平
1.西北工业大学 航天学院精确制导与控制研究所, 陕西 西安 710072 2.中国人民解放军68128部队, 甘肃 兰州 730000 3.西北工业大学 计算机学院, 陕西 西安 710129 4.西北工业大学 无人机所, 陕西 西安 710065
基于加权模糊Petri网的无人机自主任务推理决策研究
谭雁英1, 童明2, 张艳宁3, 祝小平4
1.西北工业大学 航天学院精确制导与控制研究所, 陕西 西安 710072 2.中国人民解放军68128部队, 甘肃 兰州 730000 3.西北工业大学 计算机学院, 陕西 西安 710129 4.西北工业大学 无人机所, 陕西 西安 710065
围绕无人机搜索/攻击自主任务推理决策典型想定,针对无人机自主任务推理决策规则中存在的不同输入命题对结论的贡献和影响不同,对加权模糊Petri网(weighted fuzzy petri nets,WFPN)形式化推理算法进行了深入研究;设计了双机自主搜索/攻击任务推理决策规则集;为进一步适应上述想定下规则集中存在的多条规则的输出命题是相同的情形,对WFPN形式化推理算法进行了改进;应用分层的策略,采用改进的WFPN形式化推理算法和上述设计的规则集,仿真验证了双机搜索/攻击自主任务推理结果的合理性,并降低了推算过程中矩阵的维数。
无人机;自主;加权模糊Petri网;形式化推理;分层策略;决策
无人机的高度自主智能化和多机协同是适应未来复杂多变战场环境的关键,这就要求无人机尽量减少人为干预和操控,不断提高多机协同自主推理决策能力[1]。
模糊Petri网形式化推理方法,由于具有Petri网强大的建模能力以及由模型生成矩阵,通过矩阵代数运算自动执行推理决策的优势[2],广泛应用于有人机、导弹、机器人及无人机等领域基于规则的故障诊断与推理决策中[3-7],而其在多无人机自主任务推理决策方面的应用还比较少。
本文针对多无人机自主搜索/攻击任务典型想定下推理决策规则中存在的不同输入命题对结论贡献不同的问题,对加权模糊Petri网(WFPN)形式化推理方法进行了深入研究,并为满足上述想定下存在的多条规则的输出命题是相同的情形,对WFPN形式化推理方法进行了改进。
1 WFPN形式化推理算法及其改进
1.1 WFPN的定义[8]
定义1WFPN可以定义为一个10元组:
WFPN=(P,T,D,I,O,α,β,f,Th,W)

1.2 加权模糊产生式规则的Petri网建模
加权模糊产生式规则包含许多“合取(∧)”或“析取(∨)”连接的命题,将简单规则以及它们的相互组合的规则对应的加权模糊产生式结构归结为以下3种类型[9]:
1) IFd1(w1)THENdk(μ1,λ1)。w1为输入命题的权值,通常为实数1。令y=α1·w1,当y≥λ1时,规则才能执行,那么αk=y·μ1;

图1 简单加权模糊Petri网结构及其变迁激活准则
2) IFd1(w1)∧d2(w2)∧…∧dn(wn)THEN

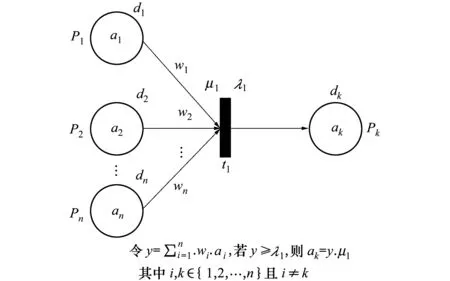
图2 合取式加权模糊Petri网结构及其变迁激活准则
3) IFd1(w1)∨d2(w2)∨…∨dn(wn)THEN
dk(μ1,μ2,…,μn,λ1,λ2,…,λn)输入命题的权系数wi都为1。令yi=αi·wi,若每条规则中的前提置信度都满足yi≥λi,那么αk=max(y1·μ1,y2·μ2,…,yn·μn)。

图3 析取式加权模糊Petri网结构及其变迁激活准则
1.3 WFPN形式化推理算法改进
文献[10]中WFPN形式化推理算法适用于产生式规则集中每条规则的输出命题是不相同的情形。为进一步适应无人机自主任务推理决策规则集中存在的多条规则的输出命题是相同的情形,本文将“⊗”算子引入到WFPN形式化推理算法中,对文献[10]的算法进行了改进,具体说明如下:
1) 算子的引入
(1) ⊕[10]:A⊕B=D,dij=max{aij,bij},其中A、B、D均为m×n维矩阵,i=1,2,…,m;j=1,2,…,n;
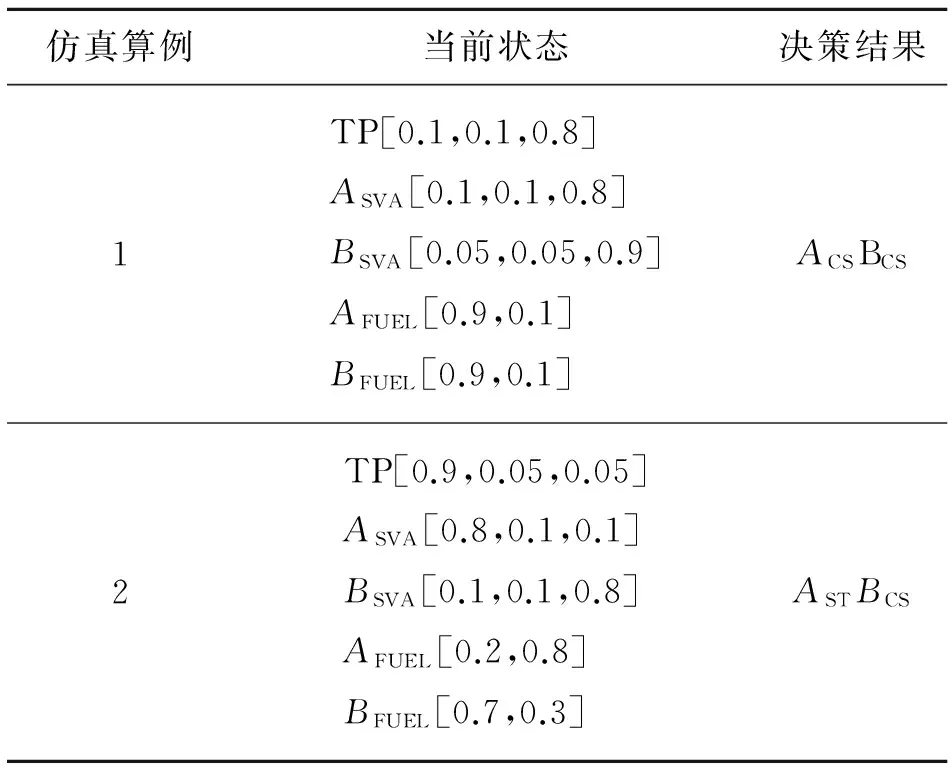
(2) ⊖[10]:A⊖B=D,如果aij≥bij,dij=aij;aij 2) 改进的推理算法 步骤1 令k=0,对向量α0,输入矩阵I,输出矩阵0,阈值向量λ进行初始化; 步骤2 计算已知客观事实条件下,变迁的输入命题组合置信度ρ=IT·αk; 步骤3 计算σ=ρ⊖λ,比较命题组合置信度ρ和变迁阈值向量λ,判断能够使能的变迁; 步骤4 激发上一步判断出的使能变迁,并计算τ=0⊗σ,同时为变迁的输入输出库所传递新的状态值; 步骤5 计算αk+1=αk⊕[0⊗((IT·αk)⊖λ)],通过得到的新的状态值,更新整个库所集的状态值; 步骤6 若αk+1≠αk,令k=k+1,重复步骤2至步骤5;若αk+1=αk,推理结束, 并输出αk+1。 2.1 双机自主任务决策典型想定 假设:在某一目标区域内有A、B两架无人机执行搜索/攻击任务,任务存在优先级之分。若小组内A、B两架无人机在所负责区域同时跟踪到同一目标时,那么A、B两架无人机将按照设计的产生式规则进行任务决策。考虑到A、B两机自主任务决策的应用需求,产生式规则的输入命题包含,攻击适合值(suitable value for attack,SVA):包括适合攻击(suitable attack,SA)、中等适合攻击(moderate suitable attack,MSA)、不适合攻击(not suitable attack,NSA),即:XSVA={SA,MSA,NSA},X=AorB;目标优先级(target priority,TP):存在高(high,H)、中(moderate,M)、低(low,L)之分,即:TP={H,M,L};剩余燃油(fuel):包括充足(enough,E)、不充足(not enough,NE),即:XFUEL={E,NE},X=AorB。 规则的输出命题包含:A攻击目标B继续搜索(Astrike target andBcontinue search,ASTBCS)、A继续搜索B攻击目标(ACSBST)、A继续搜索B继续搜索(ACSBCS)、A继续搜索B重新对准再次攻击(Acontinue search,Bredirect and attack again,ACSBRAA)、A重新对准再次攻击B继续搜索(ARAABCS)。 2.2 双机自主任务决策加权模糊产生式规则集设计 根据专家经验,设计A、B两架无人机自主任务决策加权模糊产生式规则Rule1~Rule72如表1所示。 其中Rule1具体说明如下: Rule1:IF目标优先级较高p1(0.2)AND A适合攻击p4(0.3)AND B适合攻击p7(0.1)AND A剩余燃油充足p10(0.3)AND B剩余燃油充足p12(0.1)THEN A攻击目标B继续搜索p14(μ=0.9,λ=0.6)。 Rule1~Rule72阈值和信度值均假定为μ=0.9、λ=0.6。其输入命题和输出命题的库所编号定义分别如表2和表3所示。 表1 A、B两机自主任务决策加权模糊 产生式规则集设计列表 表2 输入命题对应的库所编号定义 表3 输出命题对应的库所编号定义 2.3 基于分层的WFPN建模 本文应用分层的思想:根据设计的规则集,分别以目标优先级较高、目标优先级中等、目标优先级较低建立A、B两无人机自主任务决策的Petri网子模型,将完整的无人机自主任务决策的Petri网模型拆分成3块,如图4所示。 图4 WFPN模型分层示意图 3.1 矩阵和向量初始化 根据定义1、规则集表1以及表2、表3的定义得到各类矩阵和向量为:子模型1输入矩阵为I1、输出矩阵为O1、阈值向量为λ1;子模型2输入矩阵为I2、输出矩阵为O2、阈值向量为λ2;子模型3输入矩阵为I3、输出矩阵为O3、阈值向量为λ3。 3.2 仿真算例1 1) 仿真数据的给出 2) 推理计算 3) 推理结果分析 按照最大置信度原则,无人机决策结果为A继续搜索 B继续搜索(p18)。说明A、B两机在发现一低优先级目标后,由于A、B两机都不适合攻击,且剩余燃油都较充足,故而都采取继续搜索的策略。 3.3 仿真算例2 1) 仿真数据的给出 假定A、B两机飞行一段时间后,又同时跟踪到新的同一目标。各状态值变化为:TP[0.9,0.05,0.05]、ASVA[0.8,0.1,0.1]、BSVA[0.1,0.1,0.8]、AFUEL 2) 推理计算 3) 推理结果分析 按照最大置信度原则,无人机决策结果A 攻击目标 B 继续搜索。说明A、B两机在发现一高优先级目标后,A无人机适合攻击且剩余燃油较低,B无人机不适合攻击且剩余燃油较高,故而采取A攻击目标B继续搜索的策略。 3.4 分析说明 仿真算例1、仿真算例2决策结果如表4所示。基于WFPN形式化推理决策结果与专家决策结果相吻合,验证了A、B两机搜索/攻击自主任务推理决策结果的合理性。 表4 A、B两无人机自主飞行任务决策结果示例 本文将WFPN形式化推理方法应用于无人机搜索/攻击自主任务推理决策中,通过命题权值的引入,使得上述任务存在的不同输入命题对结论贡献大小不同的情形,在推理决策过程中得到较合理的反映;为进一步适应上述任务想定下规则集中存在的多条规则的输出命题是相同的情形,本文对WFPN形式化推理算法进行了改进;设计了两机搜索/攻击自主任务决策加权模糊产生式规则集;应用分层的策略,采用改进的WFPN形式化推理算法,仿真验证了双机搜索/攻击自主任务推理结果的合理性,并避免了计算过程中矩阵维数较高的问题。 [1] Department of Defense USA. Unmanned Aircraft Systems Roadmap2013-2038[R]. 2013 [2] 丁富玲,李承家. 模糊Petri网的发展[J]. 杭州电子科技大学学报,2008, 28(6):147-150 Ding Fuling, Li Chengjia. A Survey of Fuzzy Petri Nets[J]. Journal of Hangzhou Dianzi University,2008, 28(6):147-150 (in Chinese) [3] Gao Meimei, Zhou Mengchu. Control Strategy Selection for Autonomous Vehicles in a Dynamic Environment[C]∥Systems, Man and Cybernetics, 2005(2): 1651-1656 [4] Sun Limin, Meng Chen, Yang Sen, Li Hao. A Method for Fault Diagnosis in Missile Based on Fuzzy Petri Net[C]∥2012 International Conference on Industrial Control and Electronics Engineering,2012,5: 1911-1913 [5] Gao Meimei, Zhou Mengchu, Tang Ying. Intelligent Decision Making in Disassembly Process Based on Fuzzy Reasoning Petri Nets[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B, 2004,34(5): 2029-2034 [6] 史志富,张安,刘海燕,等. 基于模糊Petri网的空战战术决策研究[J]. 系统仿真学报,2007, 19(1):63-66 Shi Zhifu, Zhang An, Liu Haiyan, et al. Study on Air Combat Tactics Decision-Making Based on Fuzzy Petri Nets[J]. Journal of System Simulation, 2007, 19(1):63-66 (in Chinese) [7] 赵振宇,周锐,池沛. 基于模糊推理Petri网的无人机智能决策方法[J]. 兵工自动化,2015, 34(3): 71-73 Zhao Zhenyu, Zhou Rui, Chi Pei. UAV Intelligent Decision Method Based on Fuzzy Reasoning Petri Net[J]. Ordnance Industry Automation, 2015, 34(3): 71-73 (in Chinese) [8] Liu Jiufu, Chen Kui, Wang Zhisheng. Fault Analysis for Flight Control System Using Weighted Fuzzy Petri Nets[J]. Journal of Convergence Information Technology, 2011, 6(3): 146-155 [9] Chen Shyiming. Weighted Fuzzy Reasoning Using Weighted Fuzzy Petri Nets[J]. IEEE Transs on Knowledge and Data Engingeering, 2002, 14(2): 386-397 [10] 张墨华. 基于模糊Petri网的PAAIS知识处理研究[D]. 西安:西北工业大学,2006 Zhang Mohua. PAAIS Knowledge Processing Research Based on fuzzy Petri nets[D]. Xi′an, Northwestern Polytechnic University, 2006 (in Chinese) Reasoning and Decision Making for Autonomous UAVs Based on Weighted Fuzzy Petri Nets Tan Yanying1, Tong Ming2, Zhang Yanning3, Zhu Xiaoping4 1.Institute of Precision Guidance and Control, Northwestern Polytechnic University, Xi′an 710072, China 2.The Chinese People′s Liberation Army 68128 Forces, Lanzhou 730000 3.School of Computer, Northwestern Polytechnic University, Xi′an 710129, China 4.UAV Research Institute, Northwestern Polytechnic University, Xi′an 710065, China This paper is dealt with autonomous reasoning and decision-making for unmanned aerial vehicles (UAVs) executing the search and attack mission. There exists the fact in the above reasoning envision that each input proposition does different contribution to the conclusion of the rule, and so the formalized reasoning method based on weighted fuzzy Petri nets (WFPN) is studied. The weighted fuzzy production rule set about two UAVs cooperating in search and attack mission is designed. The formalized reasoning method based on WFPN is further improved to adapt to the situation that the output propositions of several rules are the same in the above rule set. Applied the layered strategy, the improved formalized reasoning method is simulated based on the designed rule set. The simulation shows that the reasoning results are reasonable and the dimension of the large reasoning matrix is reduced efficiently. unmanned aerial vehicles (UAVs), autonomous, weighted fuzzy petri nets (WFPN), formalized reasoning, layered strategy,decision making 2016-03-29 谭雁英(1967—),女,西北工业大学教授,博士,主要从事无人机自主飞行智能管理、任务规划及组合导航控制。 TP393 A 1000-2758(2016)06-0951-06
2 基于WFPN的双机自主搜索/攻击任务推理决策规则设计




3 仿真与分析
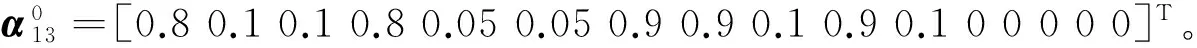
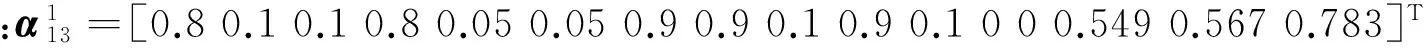

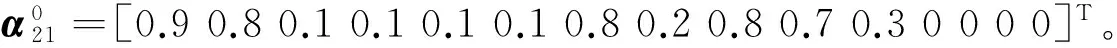

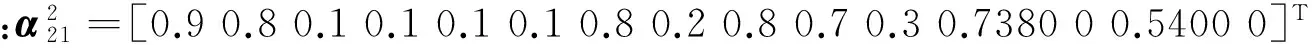
4 结 论
