无人机集群系统的运动同步稳定控制机理研究

黄汉桥, 周欢, 王勇, 张蓬, 赵鑫

1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.西北工业大学, 陕西 西安 710072 3.光电控制技术重点实验室, 河南 洛阳 471009

无人机集群系统的运动同步稳定控制机理研究

黄汉桥1,2,3, 周欢1, 王勇1, 张蓬2, 赵鑫1

1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.西北工业大学, 陕西 西安 710072 3.光电控制技术重点实验室, 河南 洛阳 471009

为保证无人机集群执行任务的可靠性和飞行安全,将集群视为具有弱连通和有向加权网络的多智能体系统,研究其运动同步稳定控制问题。首先在一致性理论的基础上提出运动同步的概念,采用反馈线性化设计具有内外回路的分布式运动同步控制机制,根据矩阵理论和Lyapunov定理分析系统的稳定性,进而得到该系统的稳定性判据。仿真结果表明:所设计的稳定控制机制不仅能够依照期望的网络拓扑实现多智能体的精确运动同步,还能够确保系统的稳定性。

多智能体;运动同步;无人机;集群;稳定控制;控制系统稳定性;反馈线性化;智能计算;线性矩阵不等式;李雅普诺夫函数;时间延迟

无人机自主协同面临的协同侦察、协同跟踪与协同打击等[1-4]作战任务需求决定了其作战使用方式是多机集群系统[5-8]。无人机集群在执行任务和飞行过程中,必须能够及时地形成相对稳定的动态队形[9],同时,根据目标任务的变化,无人机集群还必须完成队形的实时变换,在确保不发生碰撞的前提下重新取得稳定的集群队形。因此,实现无人机集群系统的稳定控制对于确保集群飞行安全和完成任务的可靠性至关重要[10-13]。

从宏观层面来说,无人机集群系统的稳定性取决于系统中无人机之间的相对位置关系,以及这种关系随时间变化的趋势和速率,此时,无人机就可以抽象为具有一定自主能力的智能体[14],而无人机集群自主协同系统的稳定控制就转化为多智能体系统的稳定控制。在多智能体系统的稳定控制方面,一致性成为当前研究热点,也是控制领域的重要研究课题[15-16]。Su等[17]通过对Olfati-Saber方法进行改进,保证了多智能体系统的一致性,Xu等[18]针对集群系统提出一种分布式的一致性协议,Hu等[19]基于对比原理方法给出了保证系统达到一致的充分条件。然而在某些情况下,完全一致是有害的。为此,谢媛艳等[20]研究了有向网络环境下一阶领导——跟随多智能体系统的滞后一致性问题,纪良浩等[21]研究了一类时延多智能系统的分组一致性问题。

对于具有leader的无人机集群系统,最终的控制目的则是使系统内部智能体在leader的引导下,其位置关系符合编队队形要求,速度达到一致性要求,这就是运动同步控制问题,该问题既需要考虑编队的控制律设计,又要考虑某些状态的一致性。然而,当前典型的编队控制方法需要针对系统中的每个智能体设计控制律,在智能体数量较大的情况下,算法过于复杂,求解效率低,且该方法要求系统必须具备全局通信能力;而单纯的一致性方法仅从宏观角度考虑控制协议问题,虽然方法简单有效,但在方法可行性和工程具体应用方面则存在诸多难题。因此,从兼顾编队控制律和一致性的角度出发,寻求一种多智能体系统的运动同步控制机制成为亟需,就我们所知,运动同步控制还未看到公开发表的研究结果。

1 问题描述与建模

令G={O,E,A}表示一个有向加权网络图,且是弱连通的。其中O={0,1,…,n}表示图G的n+1个节点集合,E⊆O×O表示图G的边集合,再令O′={1,…,n}。∀i∈O′,j∈O,图G的邻接矩阵A={aij}∈R(n+1)×(n+1),其中矩阵元素aij为节点i与节点j的连接权重,当i可以得到j的信息时,aij>0,称i与j连通,此时,图G中就存在一条有向边j→i;否则aij=0。对于节点i,将符合aij>0的所有节点j组成的集合记为Oi,Oi中元素的个数称为节点i的入度,记为ni=dim(oi),类似地,定义出度为oi。同时将所有接收节点0信息的节点的集合记为I0。

∀i∈O′,如果Oi∩I0≠ø,记:

考虑一个无人机集群,包含1个leader和n个follower,通信拓扑用上述图G表示。其中leader无人机对应节点0,follower无人机分别对应节点1到n,为确保多智能体系统能够作为一个整体,在节点1到n中,至少存在1个节点与节点0连通。

无人机集群在编队飞行过程中,通常要保持一定的飞行高度。对于二维平面内的多智能体系统,不失一般性,将无人机i的运动模型建为

(1)

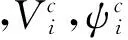
图1 任意2个智能体之间的相对位置关系

∀i,j∈O,无人机i相对于无人机j的位置pij定义为

(2)

(3)

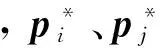
为了便于给出运动同步的定义,定义如下2个集合

(4)

2 运动同步控制机制设计

为了实现多智能体系统的运动同步,根据分布式协调控制理念,针对系统内部每个无人机成员,采用反馈线性化方法设计具有内外2个回路的分布式运动同步控制机制,其中Follower无人机i(∀i∈O′)的控制机制结构如图2所示。其中,内回路用于控制无人机i的速度和偏航,外回路通过使用局部信息(即无人机j的信息,其中j∈Oi),实现多智能体系统的稳定控制。

图2 分布式运动同步控制机制结构

假设Hi,Ki∈R2×2均是实对称的严格正定矩阵,I2×2为2×2的单位矩阵,Ci∈R2×4。令:

式中,若无人机i与leader无人机连通(即ai0>0),则γi=1;否则γi=0。

根据反馈线性化设计思路,∀i∈O,应用于无人机i的内回路控制律表示为

(5)

而对于follower无人机,即∀i∈O′,应用于无人机i的外回路控制律表示为:

(6)

式中

(7)

此时,应用于leader无人机的外回路控制律为

(8)

在内回路控制律(5)作用下,线性质点模型:

(9)

根据外回路控制律(6),∀i∈O′,可得

(10)

(11)

3 稳定性分析

(12)

同时,定义

对于所有的∀i∈O′,有:

(13)

(14)

(15)

式中

(16)

式中

(17)

式中

同时,由于存在如下2个约束条件:

(18)

M=[N1,…,Nn,N10,…,Nn0]

因而M位于拓扑PM的内部,即:

(19)

可见,在拓扑结构的每个顶点都是收敛的,这就使得(12)式中动态误差变化的广义雅可比阵是一致负定的。

定理1假设Leader智能体是由(5)和(8)式定义的闭环机制进行控制,选择使A0是Hurwitz阵的C0,同时假设O′中的每个follower智能体i的闭环控制律如(5)和(6)式所示。对某些矩阵Q=QT>0,常数λQ>0和所有Ci, i∈O′,满足下面矩阵不等式:

(20)

(21)

令:

(22)

同时,下列矩阵不等式组成立:

(23)

更保守地,满足如下不等式组:

(24)

当Hi和Ki选择作为对角矩阵hiI2和kiI2。hi和ki分别被表示为形如h1i+j′h2i和k1i+j′k2i这样的复杂形式,并且映射信号从Lp到Lp,p∈{2,∞},这里j′代表复数的虚部。

(25)

证明为了更好地证明上述定理,先给出如下引理。

(26)

(27)

式中

(28)

则：

需要注意的是,(20)式成立的一个必要条件是:

(H+Γ)-1+(H+Γ)-T>0

其服从于引理1。因此,根据不等式(20),由(29)式给出的导数会变成:

(30)

注意到:

则不等式(30)可化简为:

‖δX‖2

(31)

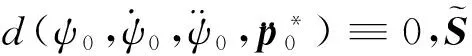
4 仿真实验与结果分析

考虑这样1个多智能体系统,包括1个leader和5个follower,其通信拓扑如图3所示。

图3 多智能体系统的通信拓扑

箭头表示智能体之间的信息流。由图中可看出,智能体1和2与leader智能体直接相连,假设控制增益为Ki,智能体3、4和5不跟leader智能体直接相连,则假设控制增益为Hi。同时,设置(1)式中控制增益分别为α=0.25和β=0.30。

互连矩阵H+Γ由下式给出:

对于Hi,Ki∈R2×2和Ci∈R2×4分别根据矩阵不等(23)式和(20)式,利用MATLAB 2013中的LMI Control工具箱进行求解,得到

假定上述多智能体系统的目标是在时间[0 100 s]跟踪如下正弦轨迹:

多智能体系统的运动轨迹、轴向位置误差及控制输入仿真结果分别如图4～图6所示。

图4 多智能体系统的运动轨迹

从图4可以看出，多智能体系统在[0 100 s]内均能够按照设置的拓扑结构保持稳定的编队队形进行飞行，并较好地跟踪正弦轨迹。为了清楚起见，图5和图6中只是给出了若干智能体的仿真曲线，其余智能体的仿真结果与其类似，可知虽然在t=50 s时刻，对该系统施加额外的控制输入后，系统的状态发生瞬变，但是多智能体很快能恢复到新的拓扑以形成新的编队队形，最终仍然能够实现运动同步和保持稳定运动状态。

图5 相对位置的误差曲线

图6 控制输入曲线

5 结 论

本文研究了无人机集群系统的运动同步控制问题，采用反馈线性化方法设计了分布式协调运动同步控制律，并基于Lyapunov定理对其稳定性进行分析，最终得到了多智能体系统运动同步的稳定控制机制。数值仿真结果表明，所设计的稳定控制机制不仅能够实现多智能体系统精确的运动同步，还能确保系统的稳定性。对多智能体系统运动同步的稳定规模控制是下一步的研究重点。

[1] Sun T Y, Huo C L, Tsai S J, et al. Intelligent Flight Task Algorithm for Unmanned Aerial Vehicle[J]. Expert Systems with Applications, 2011, 38(8): 10036-10048

[2] Pablo L, Seng K G, Eva B P, et al. Multi-UAV Target Search Using Decentralized Gradient-Based Negotiation with Expected Observation[J]. Information Sciences, 2014, 282: 92-110

[3] No T S, Kim Y, Tahk M J, et al. Cascade-Type Guidance Law Design for Multiple-UAV Formation Keeping[J]. Aerospace Science and Technology, 2011, 15(6): 431-439

[4] Manathara J G, Sujit P B, Beard R W. Multiple UAV Coalitions for a Search and Prosecute Mission[J]. Journal of Intelligent & Robotic Systems, 2011, 62(1): 125-158

[5] 段敏, 高辉, 宋永端. 智能群体环绕运动控制[J]. 物理学报, 2014, 63(14): 140204 Duan Min, Gao Hui, Song Yongduan. Distributed Encirclement Control of Multi-Agent Systems[J]. Acta Physica Sinica, 2014, 63(14): 140204 (in Chinese)

[6] Zhang W G, Liu J Z, Zeng D L, et al. Consensus of Second-Order Multi-Agent Systems with Nonuniform Time Delays[J]. Chinese Physics B, 2013, 22(5): 050511

[7] Duan H B, Luo Q N, Shi Y H, et al. Hybrid Particle Swarm Optimization and Genetic Algorithm for Multi-UAV Formation Reconfiguration[J]. IEEE Computational Intelligence Magazine, 2013, 8(3): 16-27

[8] Karimoddini A, Lin H, Chen B M, et al. Hybrid Three-Dimensional Formation Control for Unmanned Helicopters[J]. Automatica, 2013, 49(2): 424-433

[9] Zhang B C, Liu W Q, Mao Z L. Cooperative and Geometric Learning Algorithm (CGLA) for Path Planning of UAVs with Limited Information[J]. Automatica, 2014, 50(3): 809-820

[10] 茹常剑, 魏瑞轩, 沈东. 多无人机协同的稳定控制机理研究[J]. 物理学报, 2014, 63(22): 220202 Ru Changjian, Wei Ruixuan, Shen Dong. Study on Stability Control Mechanism of Multiple Unmanned Aerial Vehicle Cooperative System[J]. Acta Physica Sinica, 2014, 63(22): 220202 (in Chinese)

[11] Rajamani R, Piyabongkarn D N. New Paradigms for the Integration of Yaw Stability and Rollover Prevention Functions in Vehicle Stability Control[J]. IEEE Trans on Intelligent Transportation Systems, 2013, 14(1): 249-261

[12] Erlien S M, Fujita S, Gerdes J C. Shared Steering Control Using Safe Envelopes for Obstacle Avoidance and Vehicle Stability[J]. IEEE Trans on Intelligent Transportation Systems, 2016, 17(2): 441-451

[13] Dunbar W B, Caveney D S. Distributed Receding Horizon Control of Vehicle Platoons: Stability and String Stability[J]. IEEE Trans on Automatic Control, 2012, 57(3): 620-633

[14] Lee G, Chong N Y. Decentralized Formation Control for Small-Scale Robot Teams with Anonymity[J]. Mechatronics, 2009, 19(1): 85-105

[15] Zhu W, Cheng D Z. Leader-Following Consensus of Second-Order Agents with Multiple Time-Varying Delays[J]. Automatica, 1994, 46(12): 1994-1999

[16] Yu W W, Ren W, Zheng W X, et al. Distributed Control Gains Design for Consensus in Multi-Agent Systems with Second-Order Nonlinear Dynamics[J]. Automatica, 2013, 49(7): 2107-2115

[17] Su H S, Wang X F. Flocking of Multi-Agents with a Virtual Leader[J]. IEEE Trans on Automatic Control, 2009, 54(2): 293-307

[18] Xu X L, Chen S Y, Huang W, et al. Leader-Following Consensus of Discrete-Time Multi-Agent Systems with Observer-Based Protocols[J]. Neurocomputing, 2013, 118: 334-341

[19] Hu H X, Liu A D, Xuan Q, et al. Second-Order Consensus of Multi-Agent Systems in the Cooperation-Competition Network with Switching Topologies: A Time-Delayed Impulsive Control Approach[J]. Systems & Control Letters, 2013, 62(12): 1125-1135

[20] 谢媛艳, 王毅, 马忠军. 领导-跟随多智能体系统的滞后一致性[J]. 物理学报, 2014, 63(4): 040202 Xie Yuanyan, Wang Yi, Ma Zhongjun. Delay Consensus of Leader-Following Multi-Agent Systems[J]. Acta Physica Sinica, 2014, 63(4): 040202 (in Chinese)

[21] Ji L H, Liao X F. Consensus Problems of First-Order Dynamic Multi-Agent Systems with Multiple Time Delays[J]. Chinese Physics B, 2013, 22(4): 040203

[22] Lechevin N, Rabbath C A, Sicard P. Trajectory Tracking of Leader-Follower Formations Characterized by Constant Line-of-Sight Angles[J]. Automatica, 2006, 42(12): 2131-2141

Study on Motion Syschronization Stability Control Mechanism of Unmanned Aerial Vehicle Swarm System

Huang Hanqiao1,2,3, Zhou Huan1, Wang Yong1, Zhang Peng2, Zhao Xin1

1.Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi′an 710038, China 2.Northwestern Polytechnical University, Xi′an 710072, China 3.Science and Technology on Electro-Optic Control Laboratory, Luoyang 471009, China

In recent years, with the growing development of artificial intelligence technology, multiple unmanned aerial vehicles (UAVs), especially the UAV swarm, have been widely used in military and civilized fields. In order to ensure the flight safety and reliability of completing tasks, the motion syschronization control problem is researched in this paper by viewing the UAV swarm as a multi-agent system with the directed-weighted and weakly connected dynamic network. The concept of the motion syschronization is defined based on the consistency. Then, the distributed control mechanism with double loops is designed by using the feedback linearization method. The stability of the control mechanism is analyzed based on the Lyapunov and matrix theorem, thus obtaining its judgment criterion of stability. Finally, a simulation example is given to verify the effectiveness of the control mechanism. The results show that the proposed control mechanism can not only realize precious motion syschronization according to expected network topology, but also ensure the stability of the multi-agent system.

multi-agent system, motion synchronization, unmanned aerial vehicle(UAV), swarm, stability control, control system stability, feedback linearization, intelligent computing, linear matrix inequalities, Lyapunov function, MATLAB, time delay

2016-09-01 基金项目：航空科学基金(20155196022)、国家自然科学基金(61601505、71501184)与陕西省自然科学基金(2016JQ6050)资助

黄汉桥(1982—)，空军工程大学副教授，主要从事无人飞行器作战系统与技术研究。

V249

A

1000-2758(2016)06-0929-09