一种视觉机器人演示学习的轨迹生成方法

李建良, 杜承烈, 赵晔,3, 禹科

1.西北工业大学 计算机学院, 陕西 西安 710129; 2.西北农林科技大学 信息工程学院, 陕西 杨陵 712100 3.陕西省人民医院, 陕西 西安 710068; 4.中航工业自控所 飞行器控制一体化技术重点实验室, 陕西 西安 710065

一种视觉机器人演示学习的轨迹生成方法

李建良1,2, 杜承烈1, 赵晔1,3, 禹科4

1.西北工业大学 计算机学院, 陕西 西安 710129; 2.西北农林科技大学 信息工程学院, 陕西 杨陵 712100 3.陕西省人民医院, 陕西 西安 710068; 4.中航工业自控所 飞行器控制一体化技术重点实验室, 陕西 西安 710065

目前,机器人演示学习已成为机器人学中最为活跃的研究课题之一,而作为演示学习三要点之一的轨迹生成便成为研究热点。轨迹生成是决定演示学习是否成功的重要因素,传统上使用SIFT算法生成轨迹,但是这种方法存在很多局限,例如特征点较多、选择轨迹困难、轨迹存在一定噪声等。为此,提出了一种将SIFT、PCA和UKF等算法相结合的新的轨迹生成方法,通过实验仿真和机器人实体运行,结果表明了算法的有效性。

演示学习;SIFT算法;主成分分析;无迹卡尔曼滤波

工业机器人技术是近年来研究的热点之一,其发展状况是衡量一个国家制造业水平是否先进的主要标志[1]。大力发展工业机器人是国家发展制造业的必由之路,也是新时期顺利实现工业转型升级的必然要求[2]。随着“再工业化”的不断兴起,高端智能制造日益成为世界各国的竞争方向[3],而高端智能的发展对机器人演示学习提出了新的挑战。

近年来,机器人演示学习(learning by demonstration,LBD)已成为机器人学中最为活跃的研究课题之一[4-5]。它封装了机器人的感知能力、学习模仿能力、新技能生成能力和适应能力;可以根据环境的变化,对于给定的任务,通过自主地结合外部参数[6-7]产生运动轨迹,如学习焊接。与机器人编程的传统方法相比,LBD提供了机器人友好的教学框架[8],催生了新的研究方向,使机器人可以在社会环境中与人互动[9]。已经有许多研究者试图构建如下的模型来建立工业机器人LBD学习环境[10]:一个自然的学习环境,它可能是一个复杂的场景,有多人和多个移动目标,在不同的时间和地点发生动作。在这样的环境下,最为关键的是3个基本问题——轨迹生成、动作分解和动作重组[11,13]。轨迹生成是指机器人在LBD过程中,通过观察人或者移动目标,利用数字图像处理或外部传感器得到目标的移动轨迹,并加入相应的限制条件生成新的轨迹点,最后通过B样条插值算法生成机器人代码的过程。本文将SIFT、PCA和UKF算法相结合,构建新的轨迹生成方法,并通过实验仿真和机器人实体运行,验证算法的有效性。

1 整体设计

LBD轨迹生成的主要难点,是根据演示视频得到精确的运动轨迹。文献[8,12-13]都提到使用SIFT算法来实现演示学习轨迹的生成方法,但SIFT特征点较多,会生成大量的轨迹。因此,找出最合理的轨迹就成为研究的重点。本文提出了一种新的演示学习轨迹生成方法:首先,使用SIFT算法对演示视频进行特征提取,根据所得到的特征对相邻2帧视频进行匹配,将匹配到的特征点连线生成匹配图,并根据其坐标连线生成演示轨迹;其次,为解决生成轨迹较多、选择轨迹困难的问题,使用主成分分析法PCA(principal component analysis,PCA)对生成轨迹进行主成分提取,同时对轨迹进行降维,这不仅可去除噪声,而且可以发现其中的数据模式;最后,引入无痕卡尔曼算法,对所提取到的二维轨迹进行滤波和平滑处理,进一步消除噪声、匹配误差。其总体框架如图1所示。

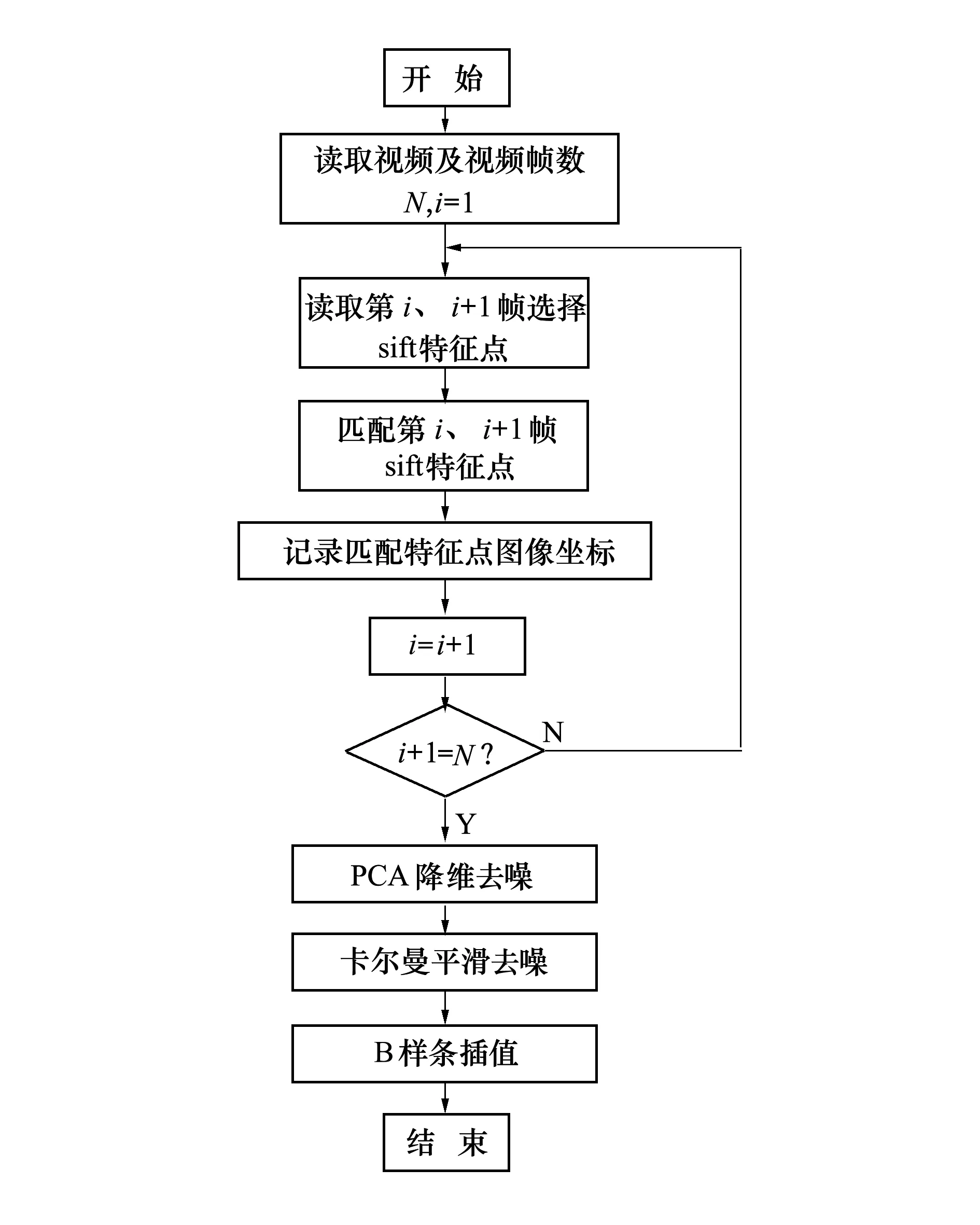
图1 整体处理流程图

2 基于SIFT算法的轨迹生成

SIFT是从不变量技术发展而来的一种特征检测方法。

2.1 尺度空间理论

尺度理论主要用来对图像数据的多尺度特征进行模拟。

二维高斯函数通常可写为

(1)

式中,σ是正态分布方差。

图像与高斯核卷积可以得到不同尺度下的尺度空间模型

L(x,y,σ)=G(x,y,σ)*I(x,y)

(2)

式中,图像的像素位置为(x,y),σ作为尺度空间因子,L称之为图像的尺度空间。

2.2 SIFT特征提取方法

1幅图像的SIFT特征向量生成算法包括如下4步操作:

1) 尺度空间极值检测,初步确定关键点位置和所在尺度。通过构造尺度空间的高斯金字塔,在图像二维平面空间和高斯差分(difference of Gaussian,DoG)尺度空间中,同时检测局部极值,作为关键特征点,以使特征点具备良好的稳定性。高斯差分图像定义为2个不同尺度的高斯核差分,它具有计算简单的特点,是归一化算子的近似,其计算公式为

(3)

式中,k为比例系数。

2) 确定稳定特征点。通过尺度空间极值检测得到备用关键特征点后,还需要将低对比度点和边缘特征点过滤掉,以提高关键点的定位精度和抗噪声干扰能力,且增加匹配时的稳定性。

3) 确定关键点的方向。在关键点所在的尺度上,利用该点邻域像素的梯度方向分布特性,为每个关键特征点指定方向参数,使算子具备旋转不变性。

4) 建立SIFT特征向量描述子。通过以上步骤,可以得到每个关键点的位置、尺度和方向信息。接下来为每个关键点建立一个特征描述子,使其对尺度、旋转、线性光照、仿射变形等宽基线变化具有一定的不变性。此外,特征描述子还能描述每个关键点的独特性,使不同特征点的特征向量之间有显著的差异。

经上述处理后,SIFT特征向量己经去除了尺度变化、旋转等因素的影响。再继续将特征向量的长度归一化,则可以进一步去除线性光照变化的影响。

2.3 SIFT描述子的特性

SIFT特征向量具有如下特性:1)多量性,即使少量的图像信息,也可以产生大量的SIFT特征;2)独特性好,具有丰富的信息,可以用于海量数据的挖掘;3)SIFT特征是图像的局部特征,具有很好的稳定性。

3 生成轨迹优化

3.1 轨迹主成分提取

主成分分析是一种基于K-L分解的多元统计方法,旨在通过研究少量主成分来显示变量之间的内部关系,因此通常将其用来提取多个变量之间的主要关系。由于基于SIFT特征生成的轨迹量较多且难以确定最优轨迹,因此本文引用PCA算法对轨迹进行提取、优化。

PCA算法对轨迹处理的步骤如下:

对于一个给定的轨迹训练集,假设训练样本数为N,先将每条路径构成一个列向量ki,i=1,2,…,N

1) 计算所有轨迹训练集的总平均路径:

(4)

2) 将每条路径减去平均路径,得到中心化轨迹

(5)

3) 将中心化后的轨迹依次作为列向量,构成矩阵

(6)

4) 计算协方差矩阵S=AAT的特征值λ和特征向量v,即

利用奇异值分解定理和K-L变换原理,通过求解ATA的特征值和特征向量,来求解AAT的特征值和特征向量。

5) AAT的正交归一化特征向量为

(7)

式中,λi为矩阵AAT的第i个非零特征值,vi为对应于λi的ATA的特征向量。

6) 将计算出来的特征值按降序排列:λ1≥λ2≥…≥λl,然后选择使得

(8)

(9)

7) 最后,便可以通过(10)式将轨迹投影到PCA子空间

(10)

PCA方法对噪声具有一定的鲁棒性,且具有完善的理论基础和较好的可操作性,按该方法选择出来的特征具有最优的表现力,因此利用该算法能够很好地解决轨迹选择问题。

3.2 轨迹滤波去噪

无迹卡尔曼滤波(unscented Kalman filter,UKF)是一种递归贝叶斯估计方法,是基于Unscented变换的一种新的卡尔曼滤波算法。其基本思想是,首先将均值和方差参数化,然后利用变换后的状态方程直接求解。该算法的实现不需要对雅可比矩阵进行显式计算,也不需要对状态方程和观测方程进行线性化。Unscented变换实际上是选择一批可表达系统状态均值和方差的采样点(称为Sigma点),经过非线性变换使这些采样点的分布以二阶精度逼近真实均值和方差。在强非线性情况下,UKF更能显示优势。

用PCA方法提取的轨迹,由于在进行SFIT特征点匹配时会产生误差,选择SFIT特征点时也会产生误差,故可将这些误差视为噪声,利用UKF滤波方法便能很好地解决此问题。

将离散非线性系统描述为

xt=f(xt-1,vt-1)

(11)

yt=h(xt,nt)

(12)

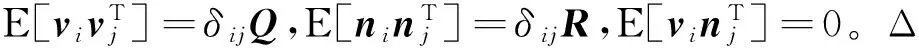
1)初始化K=1,将系统状态、状态噪声和观测噪声组成增广状态向量xa,设其维数为L,方差为Pa：

(13)

(14)

(15)

2) 计算采样点的状态向量

(16)

3) 时间更新

(17)

(18)

(19)

(20)

(21)

4) 观测更新

(22)

(23)

(24)

(25)

(26)

UKF适用于任何能用EKF解决的非线性问题。UKF不需要计算雅可比矩阵,与EKF计算量相当;UKF在计算的过程中,没有像EKF一样忽略高阶量,因此具有比EKF更高的精度。

4 实验分析

实验分2个阶段:轨迹生成阶段和机器人实体验证阶段。轨迹生成实验使用的电脑CPU为Intel Core(TM) i5-4200U(4 CPUs),CPU的处理频率为1.60 GHz;实验软件为Matlab 2015a;实验机器人为新时达SD500型机器人;实验数据为在实验室条件下使用摄像机(本文仿真分析使用的是双目摄像头中右侧摄像头所拍摄视频)所拍摄的一段长度为约为5 s、帧频为29帧/s的视频(为突出SIFT特征点,在拍摄时演示者手带白色手套,并在白色手套上涂上黑色标记),视频帧数为154,视频分辨率为640*480(部分视频图像如图2所示,图2中的a)～d)分别和图3、图4中的图像一一对应)。

图2 演示视频部分图像

图3 演示视频SIFT特征提取结果

图4 演示视频SIFT特征匹配结果

按照第一节所描述流程,首先进行SIFT特征提取,提取特征如图3所示,SIFT特征匹配结果如图4所示。从SIFT特征提取和SIFT特征匹配结果可以看出,存在一些错误的轨迹点(如瓶身上的反光点)。为获得合理的轨迹并消除这些点对轨迹造成的误差,引入PCA算法对生成的二维轨迹进行主成分提取,提取结果如图5所示。

图5 生成轨迹以及优化结果

从图5可以看出,PCA提取到了轨迹的主成分,且消除了一部分误差,但提取到的主成分“锯齿”比较严重,这些误差不利于机器人的运行,因此引入UKF对二维轨迹进行平滑处理,平滑处理结果如图5所示。

完成轨迹优化之后,利用双目标定原理和方法完成2D图像轨迹到3D空间轨迹的转换。在实验中,为了消除算法对轨迹生成的精度的影响,将3D轨迹最低点与实验对象重心重合,对3D进行处理。处理完成的轨迹在工业机器人实体上进行运行,运行结果表明:机器人能够按照预设轨迹完成对物体的抓取、移动和松绑,可以满足演示学习研究的需要,实体运行结果如图6所示。

图6 机器人实体验证

5 结 论

轨迹生成是决定演示学习是否成功的重要因素,传统上使用SIFT跟踪直接生成轨迹。但是,这种方法存在很多缺点,例如特征点较多、选择轨迹困难、轨迹存在一定噪声等等。因此,本文提出了一种将SIFT、PCA和UKF等算法相结合的轨迹生成方法。首先,通过SIFT特征点,对视频图像进行匹配,生成初始轨迹;然后利用PCA算法和UKF算法,对轨迹进行优化处理,生成最优轨迹。本文通过将由此所得的最优轨迹在机器人上进行实体运行,结果表明本文所提出的轨迹生成方法相当有效。

[1] 王田苗,陶永. 我国工业机器人技术现状与产业化发展战略[J]. 机械工程学报,2014(9):1-13 Wang Tianmiao, Tao Yong. Research Status and Industrialization Development Strategy of Chinese Industrial Robot[J]. Journal of Mechanical Engineering, 2014(9): 1-13 (in Chinese)

[2] 李睿,曲兴华. 工业机器人运动学参数标定误差不确定度研究[J]. 仪器仪表学报,2014(10):2192-2199 Li Rui, Qu Xinghua. Study on Calibration Uncertaintyof Insudtrial Robot Kinematic Parameters[J]. Chinese Journal of Scientific Instrument, 2014(10): 2192-2199 (in Chinese)

[3] 管贻生,邓休,李怀珠,等. 工业机器人的结构分析与优化[J]. 华南理工大学学报(自然科学版),2013(9):126-131 Guan Yisheng, Deng Xiu, Li Huaizhu, et al. Structural Analysis and Optimization of Industrial Robot[J]. Journal of South China University of Technology(Natural Science Edition), 2013(9):126-131 (in Chinese)

[4] Billard A, Calinon S, Dillmann R, et al. Robot Programming by Demonstration, Springer Handbook of Robotics[M]. Springer Berlin Heidelberg, 2008: 1371-1394

[5] Rozo Leonel, Jimenez Pablo, Torras Carme. A Robot Learning from Demonstration Framework to Perform Force-Based Manipulation Tasks[J]. Intelligent Service Robotics, 2013,6(1): 33-51

[6] Demiris Y, Aziz-Zadeh L, Bonaiuto J. Information Processing in the Mirrorneuron System in Primates and Machines[J]. Neuroinformatics, 2014(12): 63-91

[7] Suleman, Khawaja M U, Awais Mian M. Learning from Demonstration in Robots Using the Shared Circuits Model[J]. IEEE Trans on Autonomous Mental Development, 2014,6(4): 244-258

[8] Pagliuca Paolo, Nolfi Stefano. Integrating Learning by Experience and Demonstration in Autonomous Robots[J]. Adaptive Behavior, 2015,23(5):300-314

[9] Peters J, Vijayakumar S, Schaal S. Reinforcement Learning for Humanoid Robotics[C]∥Proceedings of the 3rd IEEE-RAS International Conference on Humanoid Robots(Humanoids), Karlsruhe, Germany, 2003:1-20

[10] Yoshikawa Y, Shinozawa K, Ishiguro H, et al. Miyamoto. Responsive Robot Gaze to Interaction Partner[C]∥Proceedings of the 2006 Robotics Science and Systems Conference, 2006: 287-293

[11] Wu Yan, Su Yanyu, Demiris Yiannis. A Morphable Template Framework for Robot Learning by Demonstration: Integrating One-Shot and Incremental Learning Approaches[J]. Robotics and Autonomous Systems, 2014,62(10):1517-1530

[12] Mitic Marko; Miljkovic Zoran. Neural Network Learning from Demonstration and Epipolar Geometry for Visual Control of A Nonholonomic Mobile Robot[J]. Soft Computing, 2014,18(5): 1011-1025

[13] Vukovic Najdan, Mitic Marko, Miljkovic Zoran. Trajectory Learning and Reproduction for Differential Drive Mobile Robots Based on Gmm/Hmm and Dynamic Time Warping Using Learning from Demonstration Framework[J]. Engineering Applications of Artificial Intelligence, 2015,45:388-404

One Path Generation Method of Visual Robot Based on BLD

Li Jianliang1,2, Du Chenglie1, Zhao Ye1,3

1.School of computer science, Northwestern Polytechnical University, Xi′an 710129, China 2.College of Information Engineering, Northwest A&F University, Xi′an 712100, China 3.Shaanxi Provincial People′s Hospital, Xi′an 710069, China 4.Science and Technology on Aircraft Control Laboratory, FACRI, Xi′an 710065, China

Robot learning by demonstration has become one of the most active research topics in robotics, and trajectory generation as one of the three points of demonstration study has become a hot research topic. Trajectory generation is decided to demonstrate learning an important factor in the success, the traditional method using sift tracking direct trajectory generation, but this method exists many shortcomings, such as more feature points selected tracks difficulties, trajectory there are certain noise, and so on. In this paper, a combination of SIFT, PCA and UKF algorithm algorithm based on trajectory generation method, the simulations and experiments with a real robot operation proves the validity of the algorithm.

learning by demonstration; scale invariant feature transform; principal component analysis; unscented kalman filter

2016-04-21

航空科学基金(20150753011)资助

李建良(1971—)，西北工业大学博士研究生，西北农林科技大学副教授，主要从事CPS系统软件工程研究。

TP391

A

1000-2758(2016)06-1082-06