基于PPCA修正模型的HRRP稳健识别方法

李彬, 李辉, 黄伟斌

(西北工业大学 电子信息学院, 陕西 西安 710129)

基于PPCA修正模型的HRRP稳健识别方法

李彬, 李辉, 黄伟斌

(西北工业大学 电子信息学院, 陕西 西安 710129)

高信噪比情况下，利用概率主成分分析(PPCA,probabilistic principal component analysis)模型识别雷达高分辨距离像(HRRP,high resolution range profile)取得了较高的识别率。但在实际工作环境中，测试阶段获取的HRRP常为低信噪比样本，由此造成的模型失配问题极大影响了识别性能。为此文章利用不同噪声来源造成的模型失配先验信息，在模型空间针对不同信噪比的测试样本补偿PPCA模型参数，以达到稳健识别的目的。另一方面，利用2种方法通过直接估计测试样本的噪声功率省去最优化计算的步骤，避免了求解最优补偿参数时需要大量计算的问题，提高了识别效率。最后，利用最大后验概率确定目标所属类别，证明了2种方法在信噪比低于20 dB时的可行性。

雷达目标识别；飞机目标探测；脉冲重复频率；高分辨距离像；概率主成分分析；模型修正

基于HRRP的目标识别一直是雷达目标识别的热门领域[1]，且一般都遵循预处理、特征提取选择、分类识别的处理流程。

HRRP的统计特征能够反映其幅度起伏特性，因此在特征提取阶段，对HRRP进行统计建模将建模问题转换为模型选择和参数估计问题[2]，能够获取可分性更高、更有价值的特征。文献[3]指出HRRP在PPCA和FA模型下近似服从联合高斯分布，提升了参数估计的效率。文献[4]在PPCA模型的基础上，利用EM算法和KL距离对HRRP重新分帧，提升了大范围方位角内HRRP的识别率。

但实际工作环境中，获取的HRRP回波由于受到目标远近、杂波和天气等因素的影响具有相对较低的信噪比，如果直接应用高信噪比环境中估计的PPCA模型参数会造成模型失配，影响识别性能[5]，这也是基于统计建模面临的普遍问题。为此相关文献从造成模型失配的原因入手，做了许多工作。文献[6]对FA模型进行非参数化修正并预先估计噪声水平，提升了小样本情况下FA模型的稳健性。文献[7]在假设HRRP各距离单元噪声服从复高斯分布的基础上，补偿不同信噪比下统计模型的参数。文献[8]利用参数寻优将基本PPCA修正为对噪声稳健的自适应PPCA模型。本文引入训练样本与测试样本模型匹配度的概念，利用噪声与信号的向量关系，得到针对不同信噪比测试样本的PPCA修正模型，增强了PPCA模型在不同信噪比环境下的稳健性。

1 模型修正和概率主成分分析

1.1 模型修正

雷达识别系统工作的典型模式是高信噪比下训练，低信噪比下识别。这使得应用PPCA模型时，不得不考虑模型在训练样本与测试样本之间的匹配问题。

从图1看出，由于受到噪声的影响，获取的PPCA模型参数ΛX={μX,WX,σX}和ΛY={μY,WY,σY}并不相同,如果使用训练样本模型ΛX,通过最大后验概率判定测试目标则必然造成识别率的下降。根据引起模型差异的原因,通过构造差异函数D1(·)、D2(·)和D3(·)消除模型间的失配,达到稳健识别的目的。

图1 训练阶段与测试阶段的信息不匹配

对于HRRP识别系统,假设训练数据集为X={x1,x2,…,xn},测试数据集为Y={y1,y2,…,yn}。在特征空间内,通过构造从测试数据集到训练数据集的映射X=Fv(Y),或在模型空间构造映射ΛY=Gη(ΛX),消除噪声的影响。可得

(1)

(2)

1.2 概率主成分分析模型

隐变量参数模型是PPCA模型的基础[9]

y=Wx+μ+ε

(3)

等式(3)中,隐变量x服从独立高斯分布N(0,I)。ε为观测噪声向量,服从N(0,ψ)。观测向量y服从N(μ,WWT+ψ)。得到模型参数为{μ,W,σ},可通过最大似然估计或期望最大值算法得到具体参数:

(4)

(5)

(6)

2 基于修正模型的稳健识别

修正PPCA模型的目的是对高信噪比条件下的模型参数进行补偿,以便准确反映不同信噪比下测试样本的分布。但是求解补偿参数是一个极值搜索问题,必然造成大量的计算。通过分析可知,不同信噪比下的PPCA补偿参数与叠加的噪声功率直接相关。如果能寻找一种估计测试样本噪声功率的方法,就可以避免求解最优化问题,降低系统的计算负担。

2.1 基于复高斯噪声的参数修正

HRRP是对采样后的复距离像取模得到的,即x=[|x(1)|,|x(2)|,…,|x(N)|]T。噪声n叠加在复数域,则任意一个距离单元内的复信号模型可表示为|x|=|s+n|。如果定义高信噪比的HRRP为|xh|,则低信噪比的HRRP为|xl|:

|xl|=|xh+n|=

(7)

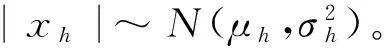
(8)

噪声与信号间的夹角θ∈[0,π],概率密度函数为:

p(θ)=1/π

(9)

利用隐函数关系f(|xl|2,wvcosθ)=0求解|xl|的密度函数p(|xl|)。令W=|xh|,v=|n|则各变量的联合密度函数为p(W2,V2,wvcosθ),首先计算cosθ的概率密度函数:

(10)

假设Z=XY,已知X,Y的联合概率密度函数f(x,y),根据(11)式计算Z的密度函数:

(11)

利用(11)式的结果计算(w,v,cosθ)的联合概率密度函数p(w,v,cosθ):

(12)

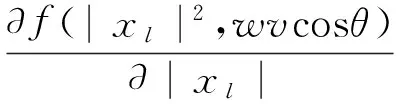
(13)

得到|xl|的概率密度函数p(|xl|):

(14)

(14)式过于复杂,修正模型意义不大。计算|xl|的近似分布。已知信号与噪声独立,期望E(|xh||n|cosθ)=0。(7)式可简化:

(15)

计算u=|xh|2和v=|n|2的概率密度函数:

(16)

(17)

由于|xh|2和|n|2独立,按照随机变量和的分布计算规则,计算z=|xl|2的密度函数:

(18)

进而得到|xl|的概率密度函数p(|xl|):

(19)

按不发生越距离单元徙动的角度为标准,将c个目标的训练HRRP划分为m帧模板。则对任意一组测试HRRP,其关于第c个目标第m帧HRRP模板的辅助函数可表示为:

(20)

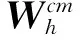
(21)

可得针对第c个目标第m帧HRRP的PPCA模型的均值修正值μ0为:

(22)

通过辅助函数f(|xl|)cm计算第c个目标第m帧HRRP的PPCA模型噪声协方差辅助矩阵φcm:

(23)

(24)

2.2 基于高斯噪声的参数修正

(25)

从(25)式可知，低信噪比条件下，HRRP幅度仍服从高斯分布。

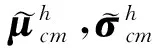
(26)

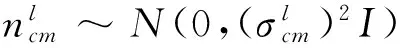
(27)

(28)

(29)

2.3 测试样本噪声功率的确定

中值滤波估计器常用来估计不同测试样本的噪声水平[11]。对于一个待测信号xn=x+n,n表示叠加的噪声,首先去除原始信号x的影响:

(30)

运算符⊗表示卷积,fdi表示i阶有限冲激响应高通滤波器。则近似的噪声信号为:

(31)

(32)

对于实HRRP信号xl,其在高斯模型下的噪声方差δ2为:

(33)

将等式(32)、(33)带入等式(22)、(24)、(28)和(29)中,得到针对不同信噪比条件下,测试HRRP的PPCA修正模型参数。

3 仿真实验

识别实验使用的HRRP数据按照文献[12]所示方法获取,包括4类飞机外形的目标A、B、C、D。采用步进频雷达,步进频2 MHz,脉冲重复频率4 KHz,步进数200,对应的HRRP距离分辨率为0.375 m,包含400个距离单元。设置4类目标的方位角变化范围为0-180°,每隔0.1°取一次回波数据作为训练样本。重新设置不同的偏航角,俯仰角和横滚角,每步进0.05°取1次回波数据作为测试样本。根据目标的横向尺寸(近似为10 m),以不发生越距离单元徙动的角度δ(MTRC)=4°,划分角域。

PPCA模型描述HRRP各个分帧的统计分布,准确性受隐变量维数q的影响。当q较低时,PPCA模型不足以描述HRRP的真实数据结构;另一方面PPCA自由参数的数量为dq+1-q(q-1)/2,当隐变量维数较多时,需要估计的参数增多,对于训练样本有限的情况,估计的精度会有所下降。针对训练样本和测试样本均为高信噪比的情况,以最大后验概率分类器检验识别结果。通过PPCA建模获取c个目标第m帧的统计参数μcm和∑cm,则对测试样本xtest的判定结果为:

(34)

图2给出了A、B、C、D类目标识别率随隐变量维数q变化的曲线,基本反映了PPCA模型描述HRRP分布的性能。

图2 各目标识别率随隐变量维数变化的曲线

(35)

高斯噪声增量下的判别规则:

(36)

图3给出了PPCA模型，基于高斯噪声的PPCA修正模型和基于复高斯噪声的PPCA修正模型在不同噪声强度下平均识别率的变化情况。

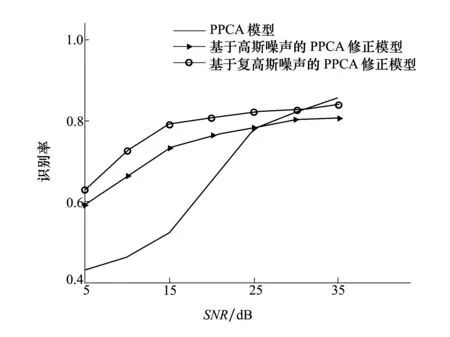
图3 PPCA模型和2类PPCA修正模型的平均识别率随信噪比变化的曲线

由图3可知，将PPCA模型应用于低信噪比测试样本的识别时，平均识别率非常低。可以这样认为，当信噪比低于20dB时，PPCA模型其实已经失效。而提出的另外两种PPCA修正模型却在低信噪比下有60%左右的平均识别率，明显的提高了识别性能，削弱了训练样本与测试样本之间的失配现象。而随着信噪比的提升，PPCA模型的平均识别率才逐步趋近于本文提出的两种PPCA修正模型。

4 结 论

在实际应用中，雷达目标识别系统获取的HRRP常处于强噪声背景中，信噪比较低，极大地影响了测试样本固有的统计特性，导致由训练样本估计的PPCA模型很难适用于测试样本。本文通过分析低信噪比信号与噪声的关系，先验的估计不同噪声源的功率，得到两种PPCA修正模型。这两种修正模型能够根据测试样本的噪声水平，修正模型参数，提高低信噪比环境下测试的稳健性。

[1] 郭尊华,李达,张伯彦,等. 雷达高距离分辨率一维像目标识别[J]. 系统工程与电子技术,2013,35(1):53-60 Guo Zunhua, LI Da, Zhang Boyan, et al. Survey of Radar Target Recognition Using One-Dimensional High Range Resolution Profiles[J]. Systems Engineering and Electronics, 2013, 35(1):53-60 (in Chinese)

[2] Liu H W, Du L, Wang P H, et al. Radar HRRP Automatic Target Recognition: Algorithm and Applications[C]∥IEEE CIE International Conference on Radar, 2011: 14-17

[3] Du L, Liu H W, Bao Z. Radar HRRP Statistical Recognition: Parametric Model and Model Selection[J]. IEEE Trans on Signal Process, 2008, 56(5): 1931-1944

[4] 王鹏辉,杜兰,刘宏伟,等. 雷达高分辨距离像分帧新方法[J]. 西安电子科技大学学报,2011,38(6):22-29 Wang Penghui, Du Lan, Liu Hongwei, et al. New Frame Segmentation Method for Radar HRRPs[J]. Journal of Xidian University, 2011,38(6): 22-29 (in Chinese)

[5] Liu H W, Chen F, Du L, et al. Robust Radar Automatic Target Recognition Algorithm Based on HRRP Signature[J]. Frontiers of Electrical and Electronic Engineering, 2012,7(1): 49-55

[6] Du L, Liu H W, Wang P H, et al. Noise Robust Radar HRRP Target Recognition Based on Multitask Factor Analysis with Small Training Data Size[J]. IEEE Trans on Signal Processing, 2012, 60(7): 3546-3559

[7] Pan M, Du L, Wang P H, et al. Noise-Robust Modification Method for Gaussian-Based Models with Application to Radar HRRP Recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2013,10(3):558-562

[8] Hou Q Y, Chen F, Liu H W, et al. Adaptive Statistical Model for Radar HRRP Target Recognition[C]∥IET Radar Conference, 2009

[9] Tipping M E, Bishop C M. Mixtures of Principal Component Analyzers[J]. Neural Compute, 1999, 11(2):443-482

[10] Gales M J F, Woodland P C. Mean and Variance Adaptation Within the MLLR Framework[J].Computer Speech & Language, 1996, 10(4): 249-264

[11] Pei Z J, Tong Q Q, Wang L N, et al. A Median Filter Method for Image Noise Variance Estimation[C]∥International Conference on Information Technology and Computer Science, 2010, 13-16

[12] 黄得双. 高分辨雷达智能信号处理技术[M]. 北京:机械工业出版社, 2001 Huang Deshuang. Intelligent Signal Processing Technique for High Resolution Radars[M]. Beijing, China Machine Press, 2001:19-31 (in Chinese)

Modified PPCA Methods for Radar HRRP Robust Recognition

Li Bin, Li Hui, Huang Weibin

(School of Electronic and Information, Northwestern Polytechnical University, Xi′an 710129, China)

In the condition of high signal-to-noise ratio(SNR), utilizing probabilistic principal component analysis(PPCA) model obtained high recognition rate in radar high resolution range profile (HRRP) recognition field. But in the actual working environment, HRRPs getting from the test phase usually have low SNR which will cause model mismatch problem influencing recognition rate. In order to get noise robust PPCA based methods, according to the prior mismatch information which are caused by different noise sources, the modified PPCA statistic parameters are computed to make up for the error of mismatch in model space. On the other hand, the two methods proposed in this paper directly estimate the increased noise power to avoid the step in solving optimization problem of modified parameters which greatly improve the calculation efficiency. Finally, in the simulation experiment applying the maximum a posteriori probability classifier to test the modified PPCA model, the results show the feasibility of these two methods below 20 dB SNR.

radar target recognition; aircraft detection; pulse repetition rate; high resolution range profile; probabilistic principal component analysis; model modification

2016-09-01

国家自然科学基金(61571364)与西北工业大学研究生创新创意种子基金(Z2016022)资助

李彬(1986—)，西北工业大学博士研究生，主要从事模式识别及雷达数据处理研究。

TN959.1

A

1000-2758(2016)06-1022-06