计算机专业数值计算方法课程教学实践的探索

樊建华 于 青

（天津理工大学，天津 300384）

计算机专业数值计算方法课程教学实践的探索

樊建华 于 青

（天津理工大学，天津 300384）

数值计算方法课程的理论性和实践性较强，本文根据计算机专业的培养目标，对该课程的教学方式进行了一些探索。课堂教学方面的一些方法显著改善了教学效果，提高了学生的学习兴趣和学习积极性。实验环节采取的一些措施使学生能够主动的参与实验过程，努力改善算法结构，提高了学生的动手实践能力和逻辑思维能力，锻炼了学生分析问题解决问题的能力。

数值计算方法；教学实践；计算机专业

一、引言

数值计算方法属于应用数学范畴，这门课程的主要目的就是研究用数字计算机求解各种数学问题的数值算法、并对其理论进行有效分析[1]。作为一门数学课程，它与其它的基础数学课程有着很大的区别，主要解决工程应用领域中的实际问题，具有很强的实践性。计算机技术的发展与普及越来越受到人们的重视，因此适用于计算机处理的数值计算方法和数据处理方法，作为科学计算的重要组成部分，已逐渐成为理工科大学本科生和研究生的必修课程[2]。现在很多高校都开设了这门课程，涉及的专业有计算机、化学、机械、食品、数学、自动化等，对工科大学的学生从事相关的专业研究具有重大的意义，由此可见该课程的重要性。

近十年来，科学技术逐渐发展进入“纳米时代”、“互联网时代”，各种高科技领域产生出大量复杂性较高的计算问题，使得发展、推广数值计算方法这门课程变得空前重要，因此这门课程越来越多地得到社会的认同。通过该课程的学习，不仅能够让学生掌握高等数学、高等代数以及程序设计方面的相关知识，更重要的是能够在解决实际问题的过程中逐步掌握科学计算的思想和方法，培养学生解决实际问题的能力[3]。因此，这门课程对计算机专业的学生来说，在实践性、创新性、程序设计能力等方面的培养具有重要的作用。

二、数值计算方法课程在教学实践中存在的问题

数值计算方法这门课程虽然不是一门新开设的课程，但是由于其中涉及到很多数学知识和公式，因此在长期的教学实践中容易存在一些问题，主要表现在以下几个方面。

1.教学重理论，轻实践

数值计算方法课程的理论和实践结合非常紧密，但是传统的教学方式侧重强调理论上的严谨性和完整性，对课程的实用性和应用性不怎么重视。实践环节方面只是要求学生运用所学的内容和方法求解或证明课后习题，使得学生不能全面地理解和运用书中所学的算法[4]。

2.教学内容组织不够严谨

数值计算方法课程中涉及的公式比较复杂，而且需要进行算法的稳定性和误差方面的分析，有一定的难度。但是大多数院校该课程安排的教学时数较少，如果使用传统的教学方法和手段，很多内容不能深入细致地讲解，导致教学效果不理想[5]。

3.注重公式的死记硬背，忽略方法产生的背景和应用

很多学生对数学方面的课程感觉很枯燥，数值计算方法课程涉及到很多定理、公式的推导，如果教师在授课的过程中没有相应的介绍这些公式所处的时代背景以及应用价值，那么久而久之，学生就会感觉所有的定理、公式都是解决某一个或某一类数学问题的符号，自然也就感到乏味[3，6]。

4.学生动手能力差，在考试中不会活学活用

在以往的教学中发现，有些学生有个错误的认识，认为只要自己把公式记住就行了，平时课上和课下很少亲自动手做题，觉得是浪费时间，没有必要。结果在考试的时候就发现，平时很多看似简单的题在实际动手做的时候就会出现各种问题，不能得到准确的最终结果。

5.在实验环节中，有些学生有畏惧心理

在上机做实验的过程中，有一部分学生认为太难了，把那么复杂的算法用C语言编写出来，觉得是一件非常困难的事情。所以有些学生从心理上有先入为主的想法，觉得这是一件自己很难完成的事情，干脆就放弃不做了，最后蒙混过关。

我校计算机科学与技术专业是天津市“十二五”重点学科，正在积极准备参加教育部的工程认证。根据工程认证的相关要求，修订了数值计算方法课程的教学和实验大纲，为了更好的培养学生的理论与实践相结合的能力，体现工程技术人员的培养目标，有必要对本课程的教学和实践环节进行探索。

三、课堂教学的改进

针对多年来学生在数值计算方法课程的学习过程中存在的一些问题，首先从课堂讲授环节就授课内容做如下的一些改进。

1.介绍有关方法的背景信息，提高学生的学习兴趣

数值计算方法课程涉及到大量抽象的公式和推导过程，而学生普遍认为数学课程比较枯燥和乏味，不容易产生兴趣。为了能够解决这些问题，本课题组采取了一些措施，通过适当介绍有关科学家的信息，尤其是我国古代非常著名的数学成就，使学生了解其实很多方法最早是由我国古代的数学家提出的，提高学生的自豪感，激发学生的学习兴趣，同时也能丰富授课内容，活跃课堂气氛。例如在讲插值法的时候可以介绍我国古代天文学家在制定历法的过程中曾对插值方法做出过杰出的贡献，譬如隋朝刘焯的杰作《皇极历》（600年）以及中唐僧一行所造《大衍历》（727年）都使用了二次插值。特别是晚唐徐昂造《宣明历》（822年）所使用的插值技术正是二阶的等距节点的牛顿插值方法，中国人这方面的工作比西方超前了上千年。

其次在教学中，还可以结合教师的研究工作，介绍计算方法在相关领域的应用，例如插值方法在图像处理中的应用，不但使学生认识到学到的知识具有实用价值，而且还可以帮助他们拓宽视野，扩大知识面。

2.通过问题分析，引入讲授内容

数值计算方法课程中最核心的内容就是求解各种数学问题的算法，这些算法都有很强的应用背景，因此在教学过程中需要讲清楚每种算法提出的背景和目的。例如在讲解数值积分这部分内容的时候，先介绍数学中求积分的牛顿—莱布尼兹公式，通过一些具体的例子分析这种方法的局限性，即对于一些比较复杂的函数无法得到原函数的时候，就不能使用牛顿—莱布尼兹公式计算函数的积分。针对这种情况，引入了数值积分的相关算法，不仅能够很容易的计算各种复杂函数的积分，而且还能计算只有函数列表没有函数表达式的积分值，关键是能在计算机上很容易编程实现。按照这样的一条思路引入相关讲授内容，学生比较容易接受新知识，理解一些数值算法的作用和意义，从而提高学习兴趣。

3.针对应用场合的不同，比较算法的优劣性

在课堂的讲授过程中除了介绍每种算法的实现原理，还应该从以下几个方面对各种算法的特点进行分析与比较，促进学生对知识的理解和掌握。

（1）算法的计算复杂性比较

算法的计算复杂性包括时间复杂性和空间复杂性，时间复杂性是指完成一个算法所需要的时间，是衡量一个算法优劣的重要参数，数值算法的时间复杂性主要根据算法运行过程中乘除法的次数来衡量；而空间复杂性是指完成一个算法所需占用的存储空间。在讲授求解同一个数学问题的多种近似算法时，应该从算法的计算复杂性对多种算法进行比较或改进。例如：在求解线性方程组的消元法中，高斯—约当消元法由于要执行归一化操作和主行之上的消元过程，所以比高斯消元法的时间复杂性要大；但是高斯—约当消元法不需要回代过程，所以编程过程更简单一些。再有在埃特金插值过程中，可以将每次线性插值结果存放到后一个插值节点单元中，从而极大的降低算法的空间复杂性，简化算法步骤。

通过这些实例的分析和比较，使学生更容易理解算法之间的区别和联系，掌握算法的精髓。

（2）数据量大小的比较

在一定的误差要求下，根据求解同一数学问题的各种算法所需的数据量大小来衡量算法的优劣，在相同的精度下，如果所需要的数据量越小，那么算法就越好。例如：给定一道数学积分问题用数值积分中的复化梯形公式和复化辛普森公式分别进行计算，使误差不超过用复化梯形公式进行计算需要使用214个等分节点的信息，但是使用复化辛普森公式只需要使用9个等分节点的信息就可以了。通过这样一些简单的例子，使学生更容易理解算法精度和误差的相关内容。

（3）算法的稳定性和误差的分析比较

在讲解每种算法时，必须进行算法的稳定性和误差的分析，这是衡量算法有效性的一个非常重要的指标，我们选择某种算法，要求它的计算结果必须能达到给定的精度。运算过程中舍入误差不增长的计算公式称为数值稳定的，只有稳定的数值算法才可能给出可靠的计算结果；否则数值是不稳定的，不稳定的数值算法毫无实用价值。

表1 第一种递推公式的计算结果

当计算到I12时开始出现负数，显然是错误的，说明这种递推公式的数值稳定性比较差，误差传播较快。接下来需要给学生分析一下之所以产生这么大的误差主要原因是根据递推公式可看出，In-1的误差扩大了5倍后传给In，因而初值I0的误差对以后每一步计算结果的影响，随着n的增大愈来愈严重，这就造成I12以后的计算结果严重失真。通过这样一组具体的数据，学生很容易理解为什么不能使用这个递推公式。

显然由计算结果可以发现第二种递推公式具有较高的精度，分析其原因是从In到In-1的计算过程中，每向后推进一步，如果In有误差的话，其舍入误差便减少为原来的1/5，因此该递推公式是稳定的。按照这样的一种思路进行讲解，通过实际的数据进行举例说明，学生比较容易接受。

算法的稳定性和误差是算法可行性的重要指标，也是算法分析的基础，通过这样的一些实际例子，让学生充分理解算法的稳定性和误差的概念，学会构造稳定性较高的算法，关键是能够对算法进行稳定性和误差方面的分析，掌握算法的精髓。

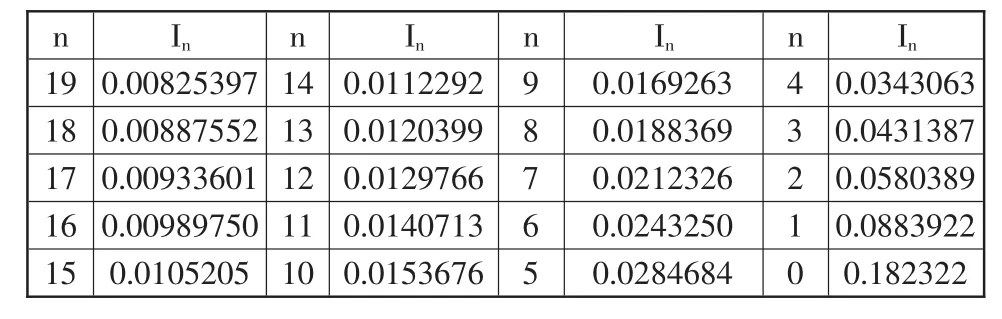
表2 第二种递推公式的计算结果

四、实验环节的改进

1.实验工具的使用

数值计算程序和其它类型的计算机程序是不完全相同的，它要求设计的程序结构严谨、语句精练。学生通常对上机实验比较怵头，因为数值计算程序要求算法的逻辑性比较强，而且实现一个程序的代码量比较多，编写过程和调试过程比较困难。数值计算方法中的很多算法在理论和实践方面都非常成熟，已经被开发并集成到专门的数学软件中，具有代表性的就是Mathematica和Matlab，这些软件数值计算功能强大，易学并且具有开放性，因此很多高校的数值计算方法课程的实验工具使用这些软件，学生不需要使用太多的计算机编程就能够实现数值计算中的各种算法，计算快捷，结果直观。对于非计算机的其它专业来说，实验的最终目的是得到各种算法在计算机上的运行效果，为各种算法解决实际问题提供依据，因此适合使用这些工具。

而对计算机专业的学生来说，较强的编程能力是他们应该具备的基本技能，而且C语言也是要求掌握的最基本最重要的一个编程工具，因此本课程要求学生使用C语言作为编程工具。这可能会增加学生实验过程的难度，但是对学生的逻辑思维和编程能力是一个很好的锻炼，能够充分体现计算机专业的培养目标和教育部工程认证的要求，对后续计算机专业课程的学习以及今后的就业都有很大的帮助。

2.实验内容的布置

为了提高实验效果，在布置每次实验内容时，应该按照由易到难这种顺序安排每次实验的任务。在最初的一两次实验中，尽量给出算法实现的关键步骤并详细讲解，给出详细的算法流程图，降低实验难度，使学生比较容易将算法编程实现，得到正确的运行结果，从而产生成就感和兴趣，树立学生的自信心，激发学生动手实践的积极性。在后续的实验过程中，对实验内容进行相应的调整，不再给出详细的算法框图，把这个算法设计环节留给学生去完成，要求学生从尽量减少计算机运行时间、尽量节省计算机存储空间、尽量使程序易读易改三个方面努力改善程序结构。通过这些基本程序的编制和改进，使学生养成办事细致谨慎、思维严谨、精益求精的好习惯，提高学生的动手实践能力和编程能力，锻炼学生的逻辑思维能力。

另一方面，将本课程和计算机的程序设计技术相结合，在每种算法的实现中单独再增加一些编程方面的要求，使得算法的运行结果具有可读性。例如在埃特金插值法和数值积分的龙贝格算法中，要求学生将每一步的计算结果按照表格的方式顺序打印输出，这样不仅使得运行结果直观容易查看，而且还能进一步锻炼学生的编程能力和C语言的应用能力。

五、结束语

随着科学技术的发展，产生大量复杂的科学计算问题，数值计算方法课程得到越来越多的重视。本文从课堂讲授和实验环节两方面对该课程的教学方式进行了一些探索，其中一些方法已经应用到计算机专业本科生的教学过程中，显著改善了教学效果，提高了学生的学习积极性。实验环节采取的一些措施使学生充分认识到上机实验的重要性，能够积极主动的参与实验过程，设计和改进算法结构，提高了学生的动手实践能力和逻辑思维能力，锻炼了学生的分析问题解决问题的能力，很好的体现了计算机专业工程认证的培养目标。

[1]张春蕊，王文龙.在“数值分析”课中重视创新实践能力的培养——兼谈研究生数学课程的教学[J].林区教学，2014（1）：84-85.

[2]胡天江，潘亮，戴斌，等.数值计算方法的融会式教学理念与实践[J].教学研究，2012（2）：53-56.

[3]赵洋，高巍.数值计算方法课程教学改革的探讨[J].辽宁教育行政学院学报，2007（5）：154-155.

[4]李云晖，韩笑锋，于景伟.计算方法课程的教学与改革[J].科技信息（科学·教研），2007（15）：64-65.

[5]李小林.关于数值计算方法课程教学改革的探讨[J].重庆文理学院学报（自然科学版），2010，29（2）：85-87.

[6]王丽.数值计算方法教学改革探究[J].科技情报开发与经济，2007，17（20）：252-253.

（责任编辑：张华凡）

Teaching and Practice of Numerical Calculation Method for Computer Major

FAN Jianhua,YU Qing
（Tianjin University of Technology,Tianjin 300384,China）

The course of numerical calculation method has a strong theoretical and practical feature.Some new teaching methods of the course have been adopted according to the training objectives of the computer major, which have improved the teaching effect significantly,and increased the students’learning interest and enthusiasm.The new ways to conduct the experiment class can enable the students to actively participate in experimental process,and make great efforts to perfect the algorithm structure,which can improve the students’hands-on skill and logical thinking abilities,and encourage them to analyze and solve problems independently.

numerical calculation method；teaching practice；computer specialty

G642.0

樊建华（1976—），女，副教授，研究方向：计算机应用。

天津理工大学校级教改项目（YB11-33）。