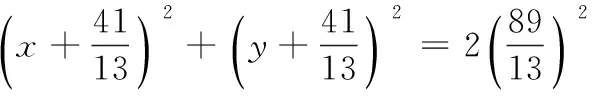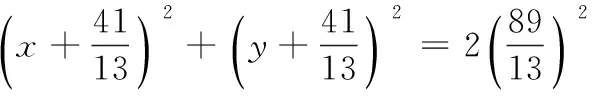巧用极限思想解题
2016-12-30方志平
方志平
(广东省惠州市第一中学,516007)
巧用极限思想解题
方志平
(广东省惠州市第一中学,516007)
在高中数学中,极限思想在解几、立几、三角、数列、函数等内容中广泛渗透,并且又衔接高等数学,起着承上启下的作用.另外,引用极限思想解题能培养学生的创新意识,唤起学生对数学的学习兴趣,激发他们的求知欲.因此,在解题教学中,我们应适时、适当引导学生巧用极限思想,开阔解题思路,提高数学素养,为将来学习高等数学打下良好的基础.
一、巧用极限思想求解解几问题
例1有一圆与直线x-y+3=0相切于点M(2,5),且经过点N(2,3),求此圆的方程.
解把直线x-y+3=0看作半径为无穷大的圆,切点M(2,5)看作半径为0的圆,设所求圆的方程为
(x-2)2+(y-5)2+λ(x-y+3)
=0.
①
将点N(2,3)的坐标代入上述方程得λ=-2,再将λ=-2代入方程并整理即得所求圆的方程x2+y2-6x-8y+23=0.
评注很多数学问题似乎与极限思想不搭界,正是在这貌似无关的表面背后隐藏着无限的玄机.本题巧用极限思想,给问题的解决带来了奇妙的效果!
二、妙用极限思想求解立几问题
例2一圆柱与圆台等高,且圆柱底面半径是圆台两底半径的等差中项,则圆柱体积V1与圆台体积V2的大小关系是( )
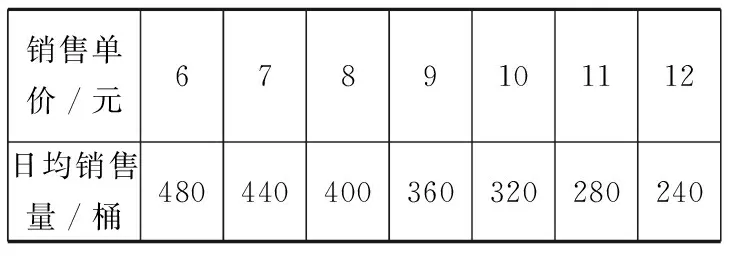
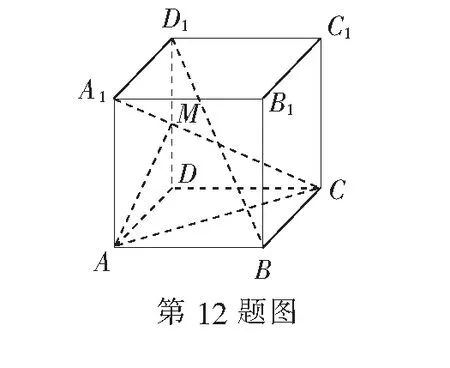
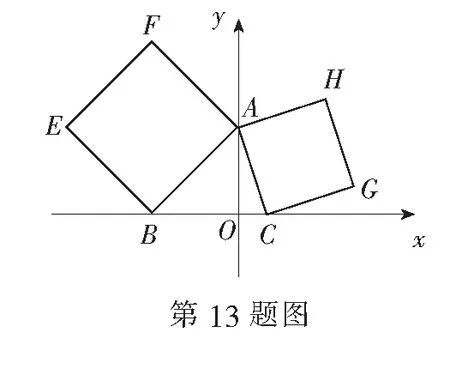
(A) V1 (C) V1>V2(D)不能确定 评注如果几何图形中有不确定的因素,那么我们就可以作为解题的一个切入点.本题正是考虑圆台底面半径不确定的因素,妙用极限思想解题,可谓独具匠心. 解∵h=c-a, ∴当c→a时h→0, 即A→0°,C→0°,B→180°时, 故选D. 评注此法化繁为简,解法新颖、独特,凸显了极限法解题的神奇功效,也彰显了数学的无穷魅力! (A) 3 (B)4 (C)某一个较大的正常数 (D) +∞ 解当n→∞时,M的值趋近于 ∴当n→+∞时,有M→+∞. 故选D. 解由已知,得 将n个等式累加,得 对此式两边取n→+∞时的极限,有 又 f(0)=1, 评注本题解法中的n是一个“设而不求”的任意正整数.先通过有限个式子,寻找一个关于n的递推关系式 再利用极限法去掉n.由此可见,利用极限思想去思考问题,往往能突破我们思维上的禁锢,拓宽考虑问题的思路,具有独创性. 当x>0且x→0时,可推得a<1. 故选A. 评注本题借用数形结合和极限的思想方法,是问题转化的重要环节.由于静态的数学问题则是动态数学问题的一个瞬时态势,因而本题极限思想的运用源于偶然,实则必然. 例7袋中有12个球,其中白球4个,黑球8个.甲、乙、丙三人接连从袋中取球,每次取一个,甲先取,然后乙、丙依次取;甲再取,然后乙、丙依次再取;如此继续下去,规定抽出的球放回,率先取出白球者获取,求甲获胜的概率. 解设“甲、乙、丙三人依次各取一次球”称为一轮.则甲可能在第一轮,第二轮,…,获胜,设“甲在第i轮获胜”的概率记为P(xi)(i=1,2,…),“甲获胜”的概率记为P(x).则P(x)=P(x1)+P(x2)+…+P(xi)+… 若甲在第i轮获胜,说明前i-1轮,甲、乙、丙均抽出了黑球,故有 所以甲获胜的概率为 P(x)=P(x1)+P(x2)+…+P(xi)+… 当i→+∞时, 评注本题使用极限思想解题,就是从无限逼近的角度去观察、分析、研究数学问题的运动、变化规律,揭示问题的本质.让我们从有限中认识了无限,从量变中认识了质变.极限思想是人类思想文化宝库中的一朵奇葩,它不仅是对数学本质的反映,也是把知识转化为能力的一种纽带. 综上,本文结合具体的例题,讨论了极限思想在高中数学中的一些巧妙应用.当然,极限思想作为数学中的重要的思想,在高中数学中的涉及范围远不止这几个方面,由于篇幅所限,在此不作赘述.不过,我们可以在教学中更多地挖掘和渗透极限思想,让学生去体会和感受这种思想方法,这样学生积淀下来的就不仅仅是数学知识,更主要的是一种数学素养. ○课外测试○ 高一数学测试 一、填空题(本大题共14小题,每小题5分,共70分) 1.若集合M=(-1,1),N=[0,2],则集合M∪N=______. 2.下面各组函数中为相同函数的是______(填序号) ④ f(x)=log2(x+1)+log2(x-1), g(x)=log2(x2-1) 3.已知log7[log3(log2x)]=0,则x-1=______. 5.设集合M={x|0≤log2x<1},N={x|x≤a},若M∩N≠∅,则a的取值范围是______. 6.若函数y=2x-(b-1)图象不经过第二象限,则b的取值范围是______. 7.设f(x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b (b为常数),则f(-1)=______. 9.已知a=log0.20.4,b=log0.20.3,c=log0.43,d=log0.30.2,则a,b,c,d的大小关系是______. 10.函数的图象y=xm2-2m-3(m∈Z,x≠0)与x,y轴都无交点,且关于y轴对称,则m为______. 11.关于x的方程|x2-1|=a有三个不等的实数解,则实数a的值是______. 12.函数f(x)是R上的奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则(x-2)f(x)<0的解集为______. 14.下列说法中:① 若f(x)=ax2+(2a+b)x+2 (其中x∈[2a-1,a+4])是偶函数,则实数b=2;② f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;③ 若函数f(x)=|2x+a|的单调递增区间是[3,+∞]),则a=-6;④ 已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.其中正确说法的序号是______(注:把你认为是正确的序号都填上) 二、解答题(本大题共6小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤) 15.(本小题满分14分)设A={x2x2+ax+2=0},B={xx2+3x+2a=0},A∩B={2}. (1)求a的值及A,B; (1)若a=1,求集合A; (2)若A∩B=A,求实数a的值. 17.(本小题满分15分)某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示: 销售单价/元6789101112日均销售量/桶480440400360320280240 请根据以上数据作出分析, 这个经营部怎样定价才能获得最大利润? 18.(本小题满分15分)已知二次函数f(x)满足f(x+1)-f(x)=2x且f(0)=1. (1)求f(x)的解析式; (2)若函数y=f(x+m)在[-1,1]上单调,求m的取值范围; (3)当x∈[-1,1]时,不等式f(x)>2x+m恒成立,求实数m的范围. x…0.511.51.71.922.1y…1475.335.115.015.01x2.22.33457…y5.045.085.6778.612.14… 20.(本小题满分16分)如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行. (1)当a=2,b=4,c=3时,求实数m的值; (3)已知h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)内任意两个变量,且x1 参考答案 一、填空题 7.-3; 8.[0,2]; 9.c 10.-1,1或3; 11.1; 12.(-3,0)∪(2,3); 13.2; 14.① ③ ④. 二、解答题 15.(1) 由2∈A,得8+2a+2=0,a=-5, 16.(1)(2-x)(x-3a-1)>0. 当a=1时,(2-x)(x-4)>0, 集合A={x|2 (2)由题意,知B=[2,+∞), 由A∩B=A,得A⊆B. ② 若2=3a+1时,不合题意; 17.根据上表,销售单价每增加1元,日均销售量就减少40桶. 设在进价基础上增加x元后,日均销售利润为y元,而在此情况下的日均销售量为 480-40(x-1)=520-40x. 由于x>0,且520-40x>0,即0 于是可得 y=(520-40x)x-200=-40x2+520x-200, 0 所以,只需将销售单价定为11.5元, 就可获得最大的利润. 18.(1)令f(x)=ax2+bx+c(a≠0).代入, 得a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x,2ax+a+b=2x恒成立. ∴a=1,b=-1, c=1, ∴f(x)=x2-x+1. (2)y=f(x+m)=(x+m)2-(x+m)+1 =x2+(2m-1)x+1-m. (3)当x∈[-1,1]时,f(x)>2x+m恒成立,即x2-3x+1>m恒成立. g(x)min=g(1)=-1,∴m<-1. 19.(1)由表中可知f(x)在(0,2]为减函数,[2,+∞)为增函数, 并且当x=2时,f(x)min=5. (2)设0 ∵0 ∴x1-x2<0,0 ∴x1x2-4<0, ∴f(x1)-f(x2)>0,即f(x1)>f(x2), ∴f(x)在(0,2]为减函数. f(x)min=f(2)=5. 20.(1)由题意,得A(2,log32),B(4,log34), C(4,logm4).又AC与x轴平行, ∴logm4=log32,m=9. (2)由题意,得 A(a,logca),B(b,logcb),C(b,logmb). ∵AC与x轴平行, ∴logmb=logca. ∵b=a2,∴m=c2, (3)∵a ∴logca 又∵a>1,b>1, ∴alogcx2 又∵logcblogca=logcalogcb, ∴logcalogcb=logcblogca. ∴alogcb=blogca ,∴alogcx2 即h[f(x2)]<φ(f(x1)) . 高二数学测试 参考公式: 2.已知直线m、n与平面α、β,给出下列三个命题: ① 若m∥α,n∥α,则m∥n; ② 若m∥α,n⊥α,则n⊥m; ③ 若m⊥α,m∥β,则α⊥β. 其中正确命题有______个. 4.已知点P是圆C:x2+y2+4x+ay-5=0上任意一点,点P关于直线2x+y-1=0的对称点在圆上,则实数a等于______. 5.已知两圆x2+y2=10和(x-1)2+(y-3)2=20相交于A,B两点,则直线AB的方程是______. 6.直线l经过点P(2,3),且在x轴上的截距等于在y轴上的截距的2倍,则直线l的方程为______. 7.正方体ABCD-A1B1C1D1中,异面直线AC与BC1所成的角为______. 8.两条平行线l1:3x+4y-2=0,l2:ax+6y=5间的距离为______. 9.点(m,0)到定点(0,2)、(1,1)距离之和的最小值是______. 11.过定点(-1,0)可作两条直线与圆x2+y2+2kx+4y+3k+8=0相切,则k的取值范围是______. 12.如图,在正方体ABCD-A1B1C1D1中,M是DD1的中点,则下列结论正确的是______(填序号) ① 线段A1M与B1C所在直线为异面直线; ② 对角线BD1⊥平面AB1C; ③ 平面AMC⊥平面AB1C; ④ 直线A1M∥平面AB1C. 13.在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以∆ABC的边AB、AC向外作正方形ABEF与ACGH,则直线FH的一般式方程为______. 二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤) 15.(本小题满分14分)已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0. (1)求直线l的方程; (2)求直线l与两坐标轴围成的三角形的面积S. 16.(本小题满分14分)如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点. (1)若平面ABC⊥平面BCC1B1,求证AD⊥DC1; (2)求证A1B∥平面ADC1. 17.(本小题满分14分)已知点P(2,-3),Q(3,2),直线l:(2-a)x-(1+2a)y+1+2a=0(a∈R). (1)求当直线l与直线PQ平行时实数a的值; (2)求直线l所过的定点(与a的值无关的点)M的坐标; (3)直线l与线段PQ(包含端点)相交,求实数a的取值范围. (1)求证:MN∥平面PCD; (2)求证:四边形MNCD是直角梯形; (3)求证:DN⊥平面PCB. 19.(本小题满分16分)如图,已知圆C:x2+y2+10x+10y=0,点A(0,6). (1)求圆心在直线y=x上,经过点A,且与圆C相切的圆N的方程; 20.(本小题满分16分)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为13,圆弧C2过点A(29,0). (1)求圆弧C2的方程; (3)已知直线l:x-my-14=0与曲线C交于E、F两点,当EF=33时,求坐标原点O到直线l的距离. 参考答案 一、填空题 4.-10; 5.x+3y=0; 6.3x-2y=0或x+2y-8=0; 12.① ② ③; 13.x+4y-14=0; 由于点P的坐标是(-2,2),所求直线l与x-2y-1=0垂直,故可设直线l的方程为2x+y+C=0.把点P的坐标代入,得2×(-2)+2+C=0,即C=2. 所求直线l的方程为2x+y+2=0. 16.(1)因为AB=AC,D为BC的中点,所以AD⊥BC. 因为平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,AD⊂平面ABC, 所以AD⊥平面BCC1B1. 因为DC1⊂平面BCC1B1,所以AD⊥DC1. (2)证法1如图16(1),连结A1C,交AC1于点O,连结OD, 则O为A1C的中点. 因为D为BC的中点,所以OD∥A1B. 因为OD⊂平面ADC1,A1B⊄平面ADC1, 所以A1B∥平面ADC1. 证法2如图16(2),取B1C1的中点D1,连结A1D1,D1D,D1B.则D1C1BD, ∴四边形BDC1D1是平行四边形, ∴D1B∥C1D. ∵C1D⊂平面ADC1,D1B⊄平面ADC1, ∴D1B∥平面ADC1. 同理可证A1D1∥平面ADC1. ∵A1D1⊂平面A1BD1,D1B⊂平面A1BD1,A1D1∩D1B=D1, ∴平面A1BD1∥平面ADC1. ∵A1B⊂平面A1BD1,∴A1B∥平面ADC1. 17.(1)kPQ=5,由l∥PQ得 (2)M(0,1). 另解:直线l与线段PQ(包含端点)相交,则 [2(2-k)+3(1+2a)+(1+2a)][3(2-a)-2(1+2a)+(1+2a)]≤0,即 (6a+8)(-5a+5)≤0, 18.(1)∵点M,N分别是PA,PB的中点, ∴MN∥AB. ∵CD∥AB,∴MN∥CD. 又CD ⊂平面PCD, MN ⊄平面PCD, ∴MN∥平面PCD. (2)∵AD⊥AB,CD∥AB,∴CD⊥AD. 又∵PD⊥底面ABCD,CD⊂平面ABCD, 所以CD⊥PD,又AD∩PD=D,所以CD⊥平面PAD. 因为MD⊂平面PAD,所以CD⊥MD. 所以四边形MNCD是直角梯形. (3)因为PD⊥底面ABCD,所以∠PAD就是直线PA与底面ABCD所成的角,从而∠PAD=60°. 从而DN2+CN2=CD2,所以DN⊥CN. 又因为PB∩CN=N,所以DN⊥平面PCB. 19.(1)由x2+y2+10x+10y=0,得 (x+5)2+(y+5)2=50. 所以圆C的圆心坐标为C(-5,-5), 又圆N的圆心在直线y=x上, 故圆N的方程为(x-3)2+(y-3)2=18. ② 当两圆内切时,设切点为M,则点M坐标为(-10,-10). 故圆N的方程为 当直线m的斜率不存在时,点C到y轴的距离为5,直线m即为y轴, 所以此时直线m的方程为x=0. 当直线m的斜率存在时,设直线m的方程为y=kx+6,即kx-y+6=0, 20.(1)圆弧C1所在圆的方程为x2+y2=169.令x=5,解得M(5,12),N(5,-12). 线段AM的中垂线方程为y-6=2(x-17). 令y=0,得圆弧C2所在圆的圆心为O2(14,0),又圆弧C2所在圆的半径为r2=29-14=15, 所以圆弧C2的方程为 (x-14)2+y2=225(x≥5). 解得x=-70(舍). 解得x=0(舍). 综上知这样的点P不存在. (3)因为EF>2r2,EF>2r1,所以E、F两点分别在两个圆弧上. 设点O到直线l的距离为d. 因为直线l恒过圆弧C2所在圆的圆心(14,0),
三、运用极限思想求解三角问题
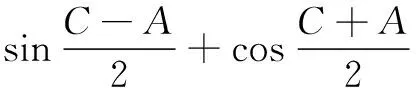
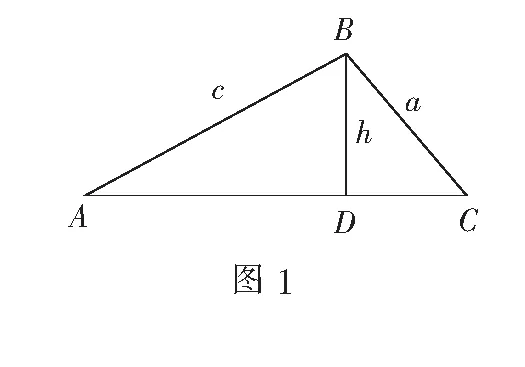
四、引用极限思想求解数列问题
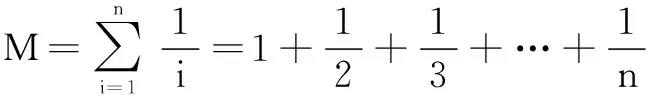


五、利用极限思想求解函数问题
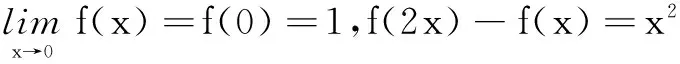

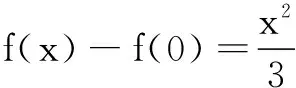

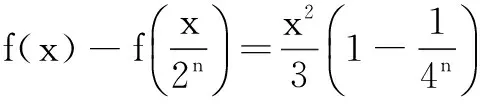
六、借用极限思想求解不等式问题



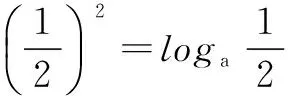

七、使用极限思想求解概率问题
















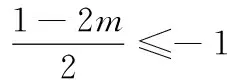

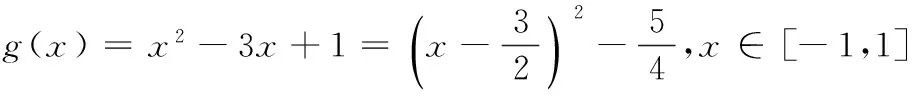
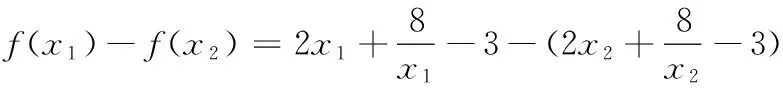




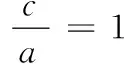
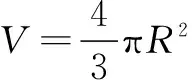












二、解答题