例析直线参数方程在解题中的应用

邹生书

(湖北省阳新县高级中学，435200)



例析直线参数方程在解题中的应用

邹生书

(湖北省阳新县高级中学，435200)

直线与圆锥曲线的综合题是高考和数学竞赛的重点和热点问题,也是高中数学教学的难点问题.这类问题综合性强，难度大,重点考查运算求解能力、推理论证能力和探究问题的能力．一般来说解题入口宽,但进入容易深入难，析出更难,运算量大,费时耗力,若方法不当则常常无功而返．对于线段长度的有关问题,若运用直线的参数方程来处理,则可简化运算提高解题效率.本文以高考题和竞赛题为例说明直线参数方程在解决这类问题中的应用．

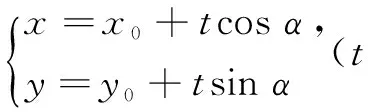
一、求定点坐标

t2sin2θ-4tcos θ-4a=0．

设t1,t2是P,Q两点对应的参数,则t1,t2是方程的两个根,由根与系数关系，得

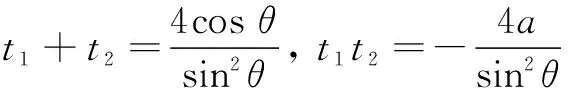
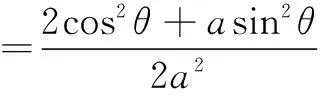
二、求参数取值

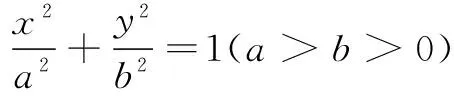
=(t1+t2)2-2t1t2

-2a2b2sin2θ-2b4cos2θ)m2

+2a2b2(a2sin2θ+b2cos2θ)].

三、求轨迹方程

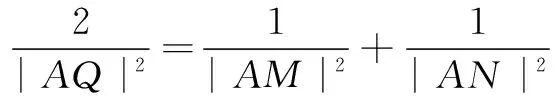
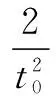
又x=t0cos θ,y=2+t0sin θ,可得

10(y-2)2-3x2=18．

四、求面积取值范围

例4(2016年全国高考题)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1，0)且与x轴不重合，l交圆A于C，D两点，过点B作AC的平行线交AD于点E.(1)求证|EA|+|EB|为定值，并写出点E的轨迹方程；(2)设点E的轨迹为曲线C1,直线l交C1于M，N两点，过点B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ的面积的取值范围.

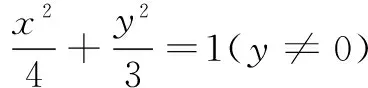
(3+sin2θ)t2+6cos θ·t-9=0,

Δt=36cos2θ+36(3+sin2θ)=144.

代入圆A的方程并整理，得

p2-4psin θ·t-12=0,

则 Δp=16sin2θ+48=16(3+sin2θ).

于是，四边形MPNQ的面积为

五、证线段等积式

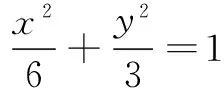
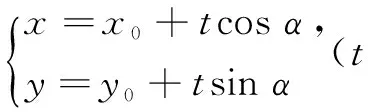
同理,设直线PT的倾斜角为β,则有

|PT|2=λ|PA||PB|．

综上可知,用直线参数方程处理线段长度和两线段长度之积等有关问题是一种行之有效的方法．用直线参数方程解题,就是利用参数的几何意义解题,思路清晰，过程简洁．参数方程在解题过程中具有化整为零、深透力强、不需分类讨论等特点,给人一种“随风潜入夜润物细无声”的诗意般的享受．