高三数学复习课微专题的教学设计与反思——以“多变量函数的值域与最值”一课为例

谢洪荣

(江苏省南京外国语学校仙林分校，210023)



○教学研究○

高三数学复习课微专题的教学设计与反思
——以“多变量函数的值域与最值”一课为例

谢洪荣

(江苏省南京外国语学校仙林分校，210023)

高三复习课基本上有三轮.第一轮主要是对基础知识及考点的全面梳理；第二轮主要是对高考中的重要知识点和方法进行专题复习；那么，到了第三轮,许多学校都是通过综合练习与回归课本,使学生熟悉应试得分的策略,提高应试的能力、技巧.今年,南京市教研室在三轮复习中新增了一种做法,就是开展微专题教学.所谓微专题,就是聚焦一个具体考点(重点、热点或难点),以专题的形式组织教学活动,一个微专题一般安排1-2节课.下面就以“多变量函数的值域与最值”为例,谈谈如何进行微专题的教学设计以及在教学过程中应该注意的问题.

一、教与学的基本认识

1. 教学目标

(1)能通过换元或消元的方法对多个变量进行减元,求解多变量函数最值与范围问题;

(2)能运用函数的性质对多个变量进行减元,求解多变量函数最值与范围问题;

(3)能运用数形结合的方法,求解多变量函数最值与范围问题.

2. 教学重点

求解多变量函数问题的基本思路与常用方法.

3. 学情分析

进入高三最后阶段的复习,学生对用导数法、基本不等式法、线性规划法求函数的值域与最值已比较熟练.对于简单的多变量函数问题,一轮复习时在相应的章节也有所涉及,但比较分散,且一轮复习的特点是从知识到方法,再到知识与方法的直接运用,理解还不够深刻；而二轮复习主要是专题复习,其特点是从问题到模式的识别,再到建立模型解决问题,重在化归及知识与方法的整合.不过二轮结束后,依然有不少同学对多变量函数问题存在盲点和疑点,因此，我们认为用微专题的形式来展开教学是比较合适的.

学生在研究多变量函数问题时,可能遇到的困难是如何观察式子的结构探寻减少变量个数的方法.因此，本专题的教学难点设定为:将多变量函数问题转化为双变量函数或单变量函数问题.

4. 教学策略分析

(1)通过学习研究,建立相应的模型

引导学生观察已知条件的结构.若已知条件是二元一次不等式组,则将目标化为二元函数,再选用几何意义或选用用基本不等式求解;若已知条件是等式或一个不等式,则考虑将目标转化为单变量函数,再运用函数的性质或利用导数求解.

(2)通过学习研究,找到降元的方法

引导学生观察已知条件的结构,若已知条件是等式,则考虑代入消元;若已知条件为二元一次不等式组,则考虑将目标先作比再换元.

(3)通过学习研究,总结解题规律

通过对基本问题的研究,学生能总结出一般的解题思路和解题方法,能综合运用所学知识解决问题,提升解决问题的能力.

二、教学过程

1. 基本问题

目标达成分析会用代入消元转化为双变量函数,运用基本不等式求最值.

目标达成分析会用分离变量后作比换元化为单变量函数,运用基本不等式求解.

答案：2.

目标达成分析将已知条件表示为分段函数,结合图形得出方程为f(x)=m(m∈R)有三个互不相等的实数根x1,x2,x3与变量m的关系,其中x2x3=m,且m=x1(2x1-1).会将目标化为关于x1的单变量函数,再求出定义域进行求解.

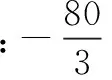
2. 方法总结

处理多变量(通常为两个或三个)函数最值或取值范围问题的基本思路是减元,常见方法有:

方法1若条件为一个等式或一个不等式可代入消元,当问题转化为双变量函数时,可考虑用基本不等式求解.

方法2若条件为不等式组可作比换元,当问题转化为单变量函数时,运用几何意义求解,或进一步用导数求解;当问题转化为双变量函数时,结合二元不等式组表示的平面区域,运用几何意义求解.

方法3利用函数的性质转化为单变量函数,确定定义域后再求解.

3. 综合应用

例1(2011年重庆高考题)若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值为______.

思路分析设2a=x,2b=y,2c=z,通过换元将已知条件中的指数方程化为整式方程,由后一个条件解出z关于x,y的表达式.令xy=t,通过换元将z化为关于t的单变量函数,并利用基本不等式由前一个条件求出xy的取值范围进而根据函数的单调性求其最值.

问题设计

(1)本题是属于多变量类型的问题吗?

(2)已知条件是什么结构?

(3)已知条件能化成更简单的形式吗?

(4)怎样进行消元?

(5)目标能化成单变量函数吗?

(6)能求出函数的定义域吗?

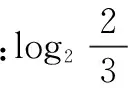
思路分析已知条件中含有三个变量,通过作比换元，转化为二元不等式组.目标转化为经过可行域内的点与原点的直线的斜率的范围问题,可行域为曲边三角形,斜率的最小值为过原点作求曲线段的切线的斜率,最大值为过两直线的交点与原点的直线的斜率.

问题设计

(1)本题是属于多变量类型的问题吗?

(2)已知条件是什么结构?

(3)已知条件能转化成二元不等式组吗?

(4)可行域表示什么图形?

(5)目标具有怎样的几何意义?

(6)临界位置在哪里?

答案：[e,7].

4. 反馈巩固

(1)设实数x,y满足x2+2xy-1=0,则x2+y2的最小值是______.

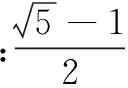
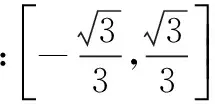
答案：10.

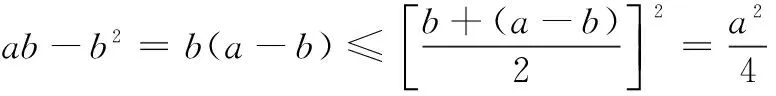
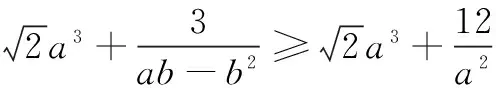
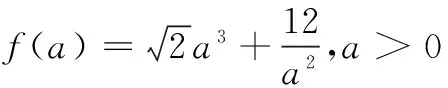
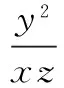
答案：3.

三、 教学反思

1. 微专题要瞄准一个点

高三最后阶段的复习主要是针对学生掌握的薄弱环节或者高考热点问题,每节课应聚焦一个问题的解决,目标明确,重点突出,删繁就简,直击要害.

2. 微专题要形成解一类问题的基本思路与方法

通过微专题的研究,在教师的引导下,通过基本问题的解决,学生能归纳出解题方法,更重要的是要形成解题思路,会根据条件和目标的要求进行合理的转化,建立适当的模型,做到有章可循,有法可依,方法有效.在此基础上,通过对典型问题的探究,学生能根据自己的体会去尝试解决问题,形成能力.通过相应的反馈巩固练习,固化学生的思维.

3. 微专题可尝试多样化的组织形式

微专题教学可以由老师讲授为主,也可以组织学生开展自主合作探究学习.我们则更多地采取了后一种方式,实践证明效果很好.具体做法是:(1)学生按照一定方式组成研究小组;(2)教师根据学情调查提供若干微专题供学生选择;(3)教师围绕每一个微专题准备一定的素材提供给学生参考;(4)学生围绕自己小组的专题，研究教师所提供的材料,并进一步收集整理相关材料,提炼解法,总结规律,形成讲稿,期间教师适时给予一定的帮助与指导;(5)各小组根据抽签顺序依次在班上进行展示交流.这种方式不仅使专题研究更加具有针对性,更因为学生经过自主研究,合作探究,公开展示的过程,使他们对于这类问题的解题思路与方法的领悟更加深刻.