一道课本例题引出圆锥曲线的三个美妙结论

武增明

(云南省玉溪第一中学，653100)



○短文集锦○

一道课本例题引出圆锥曲线的三个美妙结论

武增明

(云南省玉溪第一中学，653100)

人教普通高中课程标准实验教科书A版(2007年1月第2版)数学选修4—4“坐标系与参数方程”第38页例4:

如图1所示,AB,CD是中心为点O的椭圆的两条相交弦,交点为P.两弦AB,CD与椭圆长轴的夹角分别为∠1,∠2,且∠1=∠2，求证:|PA||PB|=|PC||PD|.

笔者在探究此例题的解答思路时,看到|PA||PB|=|PC||PD|非常象圆的相交弦定理,由此想到,若A,B,C,D四点共圆, 则|PA||PB|=|PC||PD|.进一步思考,又看到∠1,π-∠2分别是直线AB,CD的倾斜角，再结合课本中给出的此例题的解答,通过计算可知,如图1,若A,B,C,D四点共圆,那么∠1+(π-∠2)=π,即直线AB与直线CD的倾斜角互补,由此得,直线AB与直线CD的斜率互为相反数.再进一步深入探究,发现圆锥曲线如下的三个美妙结论.

结论1如果一个椭圆与一个圆相交于A,B,C,D四点,那么四边形ABCD的对边所在的直线的斜率互为相反数,两条对角线的斜率互为相反数.

证明不妨设椭圆的方程为

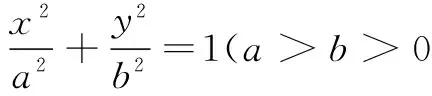
①

若圆的圆心在原点O,如图2,则由椭圆和圆的对称性可知,四边形ABCD是矩形,从而直线AD,BC的斜率都不存在,直线AB,DC的斜率都为O,直线AC与直线BD的斜率互为相反数.

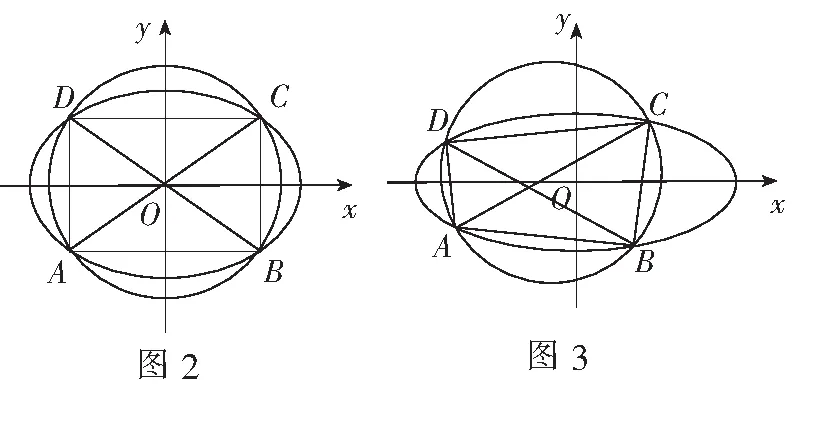
若圆的圆心不在原点O,如图3.

下面证明直线AD与直线BC的斜率互为相反数.

设直线AD与直线BC交于点P,设P(x,y),设直线AD,BC的倾斜角分别为α,β,则直线AD的参数方程为

②

将② 代入① 并整理,得到

(b2cos2α+a2sin2α)t2+2(b2x0cos α+a2y0sin α)t+(b2x20+a2y20-a2b2)=0.

③

由于b2cos2α+a2sin2α≠0,又已知直线AD与椭圆有两个交点,因此方程③ 有两个根,设这两个根分别为t1,t2,容易得到

|PA||PD|=|t1||t2|=|t1t2|

④

同理,对于直线BC,将α换为β,即得到

由圆的割线定理,得

|PA||PD|=|PB||PC|，

故b2cos2α+a2sin2α=b2cos2β+a2sin2β,

b2(1-sin2α)+a2sin2α=b2(1-sin2β)

+a2sin2β,

(a2-b2)sin2α=(a2-b2)sin2β,

∴ sin2α=sin2β,

从而sin α=sin β或sin α=-sin β(因为α,β∈[0,π),所以sin α≥0,sin β≥0，且等号在这里不会同时成立,故sin α=-sin β不成立,从而舍去),于是α=β或α=π-β.

若α=β,则此时α=β=90°,直线AD与直线BC的斜率都不存在.

若α=π-β,则直线AD与直线BC的斜率互为相反数.

仿上，可以证明直线AB与直线CD的斜率互为相反数,以及直线AC与直线BD的斜率互为相反数.

结论2如果一个双曲线与一个圆相交于A,B,C,D四点,那么四边形ABCD的对边所在的直线的斜率互为相反数,两条对角线的斜率互为相反数.

结论3如果一条抛物线与一个圆相交于A,B,C,D四点,那么四边形ABCD的对边所在的直线的斜率互为相反数,两条对角线的斜率互为相反数.

结论2、结论3的证法仿上述结论1,这里从略.

上述结论可统一为：如果A,B,C,D是圆锥曲线上任意四点,且四点共圆,那么四边形ABCD的对边所在的直线的斜率互为相反数,两条对角线的斜率互为相反数.

说明笔者查阅了大量的资料,上述结论记录在2013年11月第1版,闻杰老师编著的《神奇的圆锥曲线与解题秘诀》一书中的第140页,用动态课件探究出了上述结论,但没有给出证明.