基于弹性滑行容量的飞机有效推出时隙研究*
2016-12-30张亚平刘丽华郝斯琪邢志伟
张亚平 刘丽华 郝斯琪 邢志伟
(哈尔滨工业大学交通科学与工程学院1) 哈尔滨 150090) (河南城建学院土木与交通工程学院2) 平顶山 467036)(中国民航大学航空地面特种设备研究基地3) 天津 300300)
基于弹性滑行容量的飞机有效推出时隙研究*
张亚平1)刘丽华1,2)郝斯琪1)邢志伟3)
(哈尔滨工业大学交通科学与工程学院1)哈尔滨 150090) (河南城建学院土木与交通工程学院2)平顶山 467036)(中国民航大学航空地面特种设备研究基地3)天津 300300)
为缓解机场场面拥堵,提出基于弹性滑行容量的飞机推出控制策略.提出飞机推出时隙的概念,分析推出时隙的特性及其与滑行容量之间的关系;提出弹性滑行容量的概念,并进一步设计了飞机有效推出时隙的确定方法,建立了以飞机离港成本最低为目标的飞机推出模型.利用Arena软件对新郑国际机场飞机离港流程进行了仿真.结果表明,高峰时段平均轮候时间由6.2 min降至1.0 min,场面拥堵大大降低,离港成本下降19.3%;全天推出114架飞机中,平均推出延误时间3.8 min,推出延误超过15 min的飞机仅占4.4%.
飞机推出;有效推出时隙;弹性滑行容量;轮候时间;推出延误
0 引 言
飞机离港高峰机场跑道排队长度增加,导致机场场面拥堵、飞机离港成本增长,乘客满意度降低.合理的飞机推出时刻可以将离港飞机跑道前开机排队等待时间转化为停机位处等待时间,用虚拟排队代替物理排队,大幅降低地面油耗,Atkin等[1]在起飞排序模型研究中提到了推出时间分配问题,但未进行建模及分析.Jung等[2]运用两阶段法分配了达拉斯沃斯堡机场的飞机推出时间,Jason等[3]利用两阶段法研究了希思罗机场飞机推出决策.Simaiakis等[4-5]提出“推出率”控制的概念,并给出了建议值,接着Fornés[6]研究了飞机停机位限制及相关约束.杨双双等[7]分析飞机场面运动状态并进行了数学编码,提出基于场面监视雷达系统的滑行推出许可决策启发式控制方法.
文中采用“推出控制”的方法研究飞机推出决策问题.为了促进推出需求时间分布的均衡,提出“推出时隙”的概念,为了充分利用场面资源又不会超出管制员管制能力,提出“弹性滑行容量”的概念,并在此基础上提出飞机有效推出时隙的确定方法,建立以飞机离港成本为目标的飞机推出模型.最后对新郑国际机场进行仿真分析.
1 推出时隙
1.1 推出时隙概念及特性
为了调整同一时段内的推出时间,提出推出时隙的概念,运用推出时隙将时段进行划分,平衡飞机推出作业的时空分布.
参照机场时隙的概念[8],飞机推出时隙定义为:机场赋予飞机的推出许可,获得这个许可之后,航空公司就可以在某个具体的时间段内来完成飞机的推出动作,推出时隙可以用推出时隙的开始时刻、持续时间段、结束时刻进行描述.
推出时隙实际上就是一架飞机完成推出的时间段,具体见图1.

图1 飞机推出时隙概念
推出时隙1“06:00-06:20”表示该时隙的开始时间为06:00,结束时间为06:20,在持续的20 min的时间段内,飞机可以完成推出运行,推出时隙的长度取决于所在时段,繁忙时段推出时隙短,非繁忙时段长,相邻两个推出时隙的长度也不一定相同,其长度的动态变化体现滑行量、起飞量与到达量的相互关系.
推出时隙与起降时隙的区别在于:起飞时隙时段长度一般相等且较短,起飞时隙开始时刻,授权飞机必须开始起飞滑行,而推出时隙长度不一定相等,长短由场面拥挤程度决定,推出时隙开始时刻授权飞机未必开始推出,以推出时隙1为例,持续时间为20 min,航空公司可以视具体情况选择在06:00-06:18(假设飞机推出时间为2 min)之间的任意时刻开始推出,体现航空公司的自主决策能力在资源分配过程中的参与,这些具体情况,如地面成本最小、乘客人均等待最小等.
1.2 滑行容量与推出时隙
P(t),T(t),A(t)为在t时段内飞机推出量、起飞量,到场量;N(t)为滑行飞机量/起飞需求,指在t时段末场面滑行的滑行量,即已经推出、未起飞的飞机总量,本质上即该时段的滑行量,N(t)=N(t-1)+P(t)-T(t).
1) 滑行容量NCAP(t) 某一指定时段场面允许的最多滑行航空器架次.
2) 滑行容量NCAP(t)与推出时隙 允许推出时隙数量与允许滑行飞机架次紧密联系,因此场面滑行容量决定推出时隙数量.滑行容量值确定,则推出时隙数量确定,例如某一个t时段(t=15 min)的滑行容量为15架,起飞量T(t)为9架,则在该15 min内可以有6个飞机推出,推出时隙数量为6个,每个推出时隙长度为2.5 min,推出率为6架/15 min,实际推出飞机数量(0,6],视推出需求而定.
3) 弹性滑行容量NECAP(t):NECAP=[N*,N*+1] 当场面上的滑行量达到临界值N*,离场飞机的起飞率不再增加,此时若继续推出1架飞机,虽然起飞率不再增加但是可以充分利用机场资源且不会超出管制员管制能力,然而持续推出飞机数量过多又将会导致场面拥堵.因此对于飞机推出决策来讲,将场面滑行容量值控制在一定范围更有利于对飞机推出进行动态控制.鉴于此,场面滑行容量为区间值[N*,N*+1],即弹性滑行容量.
4) 弹性滑行容量NCAP与有效推出时隙NCAP确定后即可计算得到有效推出时隙数量,例如某t时段滑行容量为[15,16],已知起飞量T(t)为9架,则在该t时段内有效推出时隙[6,7](t=15 min时每个有效推出时隙长度为2.1 min或2.5 min),实际推出飞机数量(0,7],视具体情况而定.
2 有效推出时隙的确定方法
2.1 场面滑行容量估算
起飞量可以表达为滑行量和到场量的函数[9]:给定m对N(t),T(t),A(t)值(x1,y1,z1),(x2,y2,z2),…,(xm,ym,zm),寻找一个非减凹函数g:R2→R估计起飞量均值T=g(N,A(t)),函数中N(t),A(t)全部定义在自然数域,估计g(0,0),g(0,1),g(0,2),…,g(l,n).其中n=maxN(t);l=maxA(t);g为N(t),A(t)的一个分段线性函数.
(1)
(2)
g(i+1,j)≥g(i,j)
i=0,1,…,(n-1),∀j
(3)
g(i+1,j)-g(i,j)≤g(i,j)-g(i-1,j)
i=1,…,(n-1),∀j
(4)
g(i,j+1)≤g(i,j)
j=0,1,…,(l-1),∀i
(5)
g(i,j+1)-g(i,j)≤g(i,j)-g(i,j-1)
j=0,1,…,(l-1),∀i
(6)
g(i+1,j)-g(i,j)≥
g(i+1,j+1)-g(i,j+1)
i=0,1,…,(n-1);j=0,1,…,(l-1)
(7)
g(i,j)-g(i,j+1)≤
g(i+1,j)-g(i+1,j+1)
i=0,1,…,(n-1);j=0,1,…,(l-1)
(8)
式(3)~(4)表示对于固定到场量,起飞量是滑行量的单调非减凹函数;式(5)~(6)表示对于固定滑行量,起飞量是到场量的非减凹函数;式(7)可以确保增加滑行量、降低到场量时起飞量的边际收益;式(8)可以确保降低到场量、降低滑行量时起飞量的边际收益.在这些约束条件下,起飞量可以表达为滑行量、到场量的函数y=g(x,z).
2.2 有效推出时隙计算步骤
将每天07:00~17:00按照15 min的间隔划分时段,根据飞机的准备好推出时间、实际起飞时间、实际落地时间分别统计出每个时段内P(t),T(t),A(t)作为基础数据,有效推出时隙计算步骤如下.
步骤1 使用Matlab对不同达到率A(t)下,N(t)和T(t)进行曲线拟合.
步骤2 已知当前滑行量N(t-1)和未来15 min内的到场量A(t),通过第一步得到的曲线预测未来15 min的起飞量T′(t).
步骤3 通过分析T′(t)的变化找到起飞量停止点对应的N*(t)值,得到NECAP(t)的取值范围.
步骤4 当前滑行量N(t-1)减去未来15 min的起飞量T′(t),得到在未来15 min内仍在滑行但未能起飞的飞机量N′(t).
步骤5 使用NECAP(t)减去第4步中的值,得到在未来15 min内期望推出的飞机量范围.
步骤6 第5步中得到的值即为未来15 min有效推出时隙数量Nslot(t).如期望推出飞机量为[10,11]架次,则推出时隙数量10~11个,每个时隙长度1.36~1.5 min.
3 基于有效推出时隙的飞机推出模型
3.1 模型基本假设
(1)离港过程成本只有APU油耗、滑行及轮候油耗、延误成本,暂不考虑其他费用;(2)暂不考虑飞机优先权,按照推出申请时刻先后排序,即推出顺序与先到先服务(first come first serve,FCFS)相同,推出时刻与FCFS不同;(3)为了不增加管制员负荷,不改变顶推及滑行方案,则推出时间为已知,滑出时间为一随机时间,符合一定的概率分布;(4)暂不考虑航空公司推出时刻选择,即飞机在对应时隙的开始时刻推出.
3.2 飞机推出系统建模
根据假设(1),飞机i的离港过程成本ci为
(9)

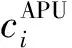
(10)


(11)
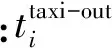

(12)

地面运行成本C最低目标表达式
(13)
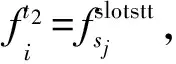
(15)

4 仿真分析
4.1 有效推出时隙确定与推出延误验证
将2~4月份所有N(t),T(t)按照到场量A(t)分组,使用Matlab对不同达到率A(t)下,N(t)和T(t)进行曲线拟合,见图2.
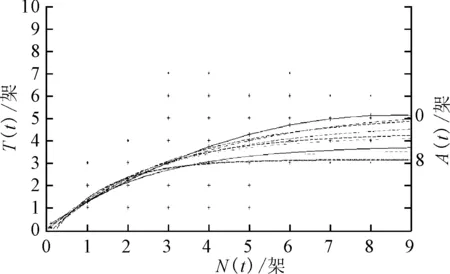
图2 不同到场量下离场量与起飞量的拟合曲线
图2是对应于该跑道配置的滑行容量曲线,对于不同的飞机到达量,起飞量停止点有差异,以A=0为例,当临界值N*为7架时起飞量达到饱和值5AC/15 min,场面滑行的滑行量继续增加,起飞数量不再增长,此时如果持续推出过多飞机,将造成场面飞机堆积,极易产生拥堵;随着到场量的增长,曲线趋于平稳,当A=8,N=3时起飞量达到饱和值3AC/15 min,此时若持续推出飞机(超过4架或者更多),起飞飞机数量不再增长,飞机全部集中在场面,导致拥堵.
使用当前滑行量N(t-1)和未来15 min内的到场量A(t)预测未来15 min的起飞量T′(t);分析T′(t)的变化找到起飞量停止点对应的N*(t)值,得到各15 min内NECAP(t);N(t-1)-T′(t)=N′(t);NACP(t)减去N′(t),得到在未来15 min内期望推出的飞机量,最终得到有效时隙数量范围,见表1.
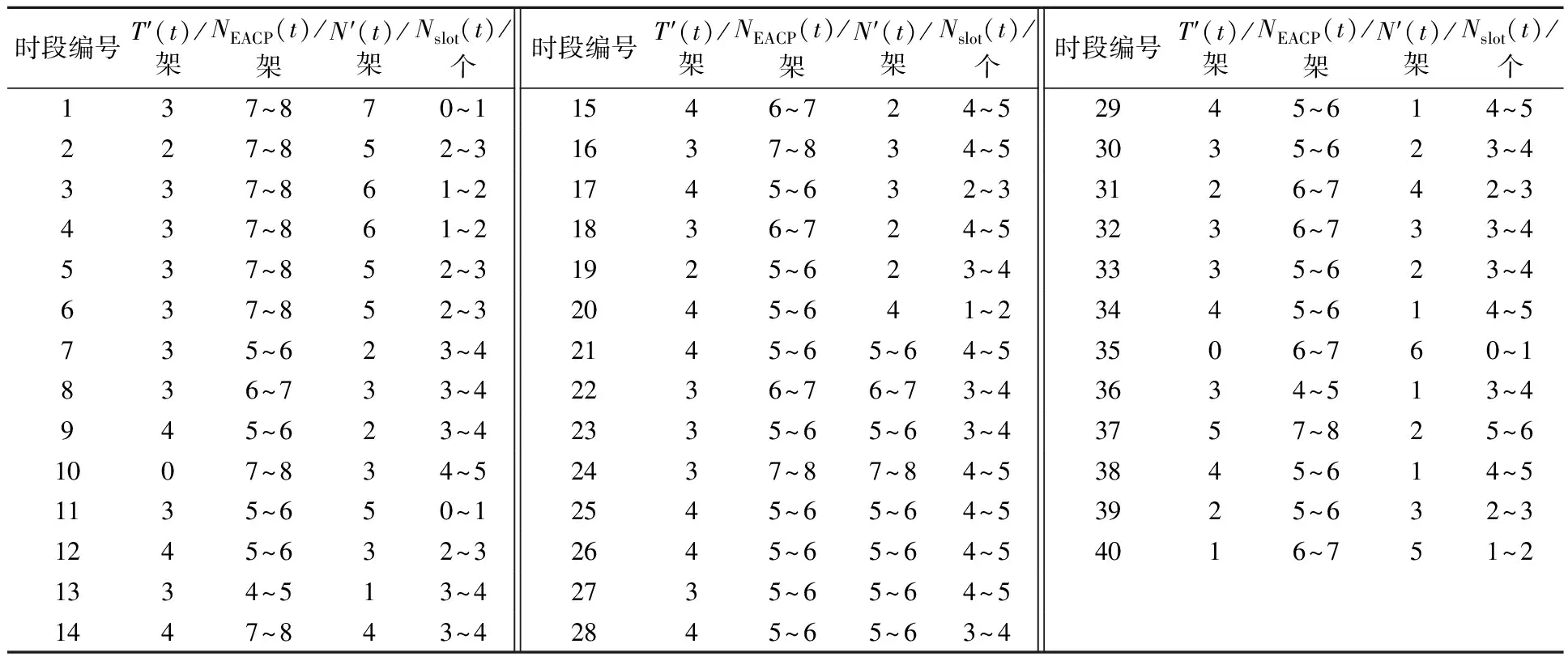
表1 有效时隙数量计算表
表中时段编号依次为07:00-07:15,07:15-07:30,…,16:45-17:00.

由表2可知,有效时隙数量Nslot(t)与计划推出飞机数量P(t)在各时段基本相等,仅在特殊时段有较大差别:09:00-10:00内8架飞机推出需求集中于09:30-10:00,而09:30-10:00的高到场量又限制了弹性滑行容量,3架飞机延迟到10:00之后推出,导致09:50-11:00之间产生了较大推出延误.
小时推出延误除特殊时段外均处于较低水平,均值3.51 min;单架飞机推出延误均值3.8min/架,114架飞机推出延误分布:0~5 min 75架(65.8%),5~10 min 23架(20.2%),10~15 min 11架(9.6%),15~20 min 5架(4.4%),20 min 0架,虽然较FCFS存在一定程度的推出延误,但仅14%的飞机延误超过10 min,表明推出延误能够控制在较低水平.

表2 有效时隙及推出延误
4.2 基本参数
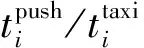

表3 仿真基本参数
注:资料来源:河南省机场集团有限公司.
4.3 Arena仿真分析
离港过程建模 以计划离港时间为流程的开始,经过停机位等待、推出、滑行、轮候,最后起飞,利用Arena建模,并逐项输入仿真参数.



图3 飞机轮候时间对比图
虽然有效时隙控制比FCFS的停机位等待时间长,但是经过仿真优化,平均轮候时间缩短了5.2 min,停机位等待和轮候的单位油耗成本分别为5/29.4~29.8元/min,因此地面油耗大幅下降,离港成本由20 487.9元降至16 540元,下降19.3%.原因:有效时隙控制下,推出时间实现由集中(FCFS)向分散,缓解场面拥堵、缩短离港滑行及轮候时间,进而降低离港成本.
5 结 论
1) 飞机推出时隙概念的提出,能够分散飞机推出作业的集中,均衡推出需求.
2) 提出弹性滑行容量的概念,并给出滑行容量预测的方法.与以往不同之处在于,滑行容量值为区间值,在满足场面滑行需求的同时又能充分利用场面资源.
3) 基于弹性滑行容量的飞机有效推出时隙的方法的提出,能够大幅缓解场面拥堵,同时将飞机推出控制带来的延误控制在较低水平.
[1]ATKIN J A D, BURKE E K, GREENWOOD J S. A comparison of two methods for reducing take-off delay at London Heathrow airport[J]. Journal of Scheduling,2011,14(5):409-421.
[2]JUNG Y, HOANG T, MONTOYA J, et al. Performance evaluation of a surface traffic management tool for dallas/fort worth international airport[C]. Ninth USA/Europe Air Traffic Management Research and Development Seminar,2011:1-10.
[3]JASON A D, GEERT D M, EDMUND K B, et al. Addressing the pushback time allocation problem at Heathrow Airport[J]. Transportation Science,2012,47(4):584-602.
[4]SIMAIAKIS I. Analysis modeling and control of the airport departure process[D]. Cambridge: Massachusetts Institute of Technology,2013.
[5]SIMAIAKIS I, KHADILKAR H, BALAKRISHNAN H, et al. Demonstration of reduced airport congestion through pushback rate control[J]. Transportation Research Part A: Policy and Practice,2014,66:251-267.
[6]FORNéS MARTINEZ H. Analysis of potential implementations of pushback control at LaGuardia airport[D]. Cambridge: Massachusetts Institute of Technology,2015.
[7]杨双双,朱华庆.航空器推出决策的优化研究[J].武汉理工大学学报(交通科学与工程版),2014,38(1):227-231.
[8]胡明华.空中交通流量管理理论与方法[M].北京:科学出版社,2010.
[9]PUJET N. Modeling and control of the departure process of conjested airports[D]. Cambridge: Massachusetts Institute of Technology,1999.
[10]赵向领,唐建勋,卢飞,等.基于改进离散差分算法的航班延迟推出策略分析[J].交通运输系统工程与信息,2015,15(6):114-120.
Aircraft Effective Pushback Slot Based on Elastic Taxiing Capacity
ZHANG Yaping1)LIU Lihua1,2)HAO Siqi1)XING Zhiwei3)
(SchoolofTransportationScienceandEngineering,HarbinInstituteofTechnology,Harbin150006,China)1)(SchoolofCivilandTransportationEngineering,HenanUniversityofUrbanConstruction,Pingdingshan467044,China)2)(GroundSupportEquipmentResearchBase,CivilAviationUniversityofChina,Tianjin300300,China)3)
In order to alleviate the congestion of airport surface, an aircraft pushback control strategy based on elastic taxiing capacity is explored. The concept of the “aircraft pushback slot” is proposed, and the characteristic of pushback slot is analyzed. The concept of “elastic taxiing capacity” is put forward, and the calculation method of aircraft effective pushback slot is further designed. Then, an aircraft pushback model for minimizing the total cost of departure process is established. A simulation is performed on Xinzheng International Airport with Arena. The result shows that the average waiting time during rush hour is reduced from 6.2 min to 1.0 min, the congestion is alleviated, and the total cost is decreased by 19.3%. Among the 114 departures of the whole day, the average pushback delay is 3.8 min, and the proportion of pushback delays which exceeding 15 min only account for 4.4%.
aircraft pushback; effective pushback slot; elastic taxiing capacity; waiting time; pushback delay
2016-09-31
*国家自然科学基金项目资助(U1233124,61179069)
U8
10.3963/j.issn.2095-3844.2016.06.001
张亚平(1966—):男,博士,教授,主要研究领域为交通流特性、机场地面运行调度与控制
