第一阶段单纯形法的一种分段定价策略
2016-12-28高培旺
高培旺
(闽江学院,福建 福州 350121)
第一阶段单纯形法的一种分段定价策略
高培旺
(闽江学院,福建 福州 350121)
提出第一阶段单纯形法的一种分段定价策略,而在此策略下可产生两种单纯形算法变式.根据Cheng的判断准则将所有非基变量分成四段,其中一段由最优基本解中的非基变量构成,在迭代过程中对另外三段非基变量依其保持非基的可能性程度先后交替定价.第一种算法从迭代开始就根据Cheng的两个判断准则对四段非基变量不断调整,这虽极大节省了定价计算的工作量,但两个判断准则的计算需要耗费大量时间,导致该算法计算效率很低.第二种算法对第一种算法作了改进,当目标当前值超过最优值的2/3时,开始对非基变量分段,然后只根据Cheng的一个较简单的判断准则对定价后的非基变量进行调整.对来自NETLIB和MIPLIB的27个典型算例的初步试验结果表明,改进的算法不仅比经典单纯形算法所用的总迭代次数要少,在所有算例上所搜寻的非基列数也少,所耗费的计算时间更少,其计算性能高效而稳定.
线性规划;单纯形法;定价准则;分段定价;计算效率
考虑如下形式的线性规划问题:
(LP) maxf=cx
s.t.Ax=b,
x≥0,
这里,A=(A1,A2,…,An)∈Rm×n(m 求解(LP)的单纯形算法首先需要一个初始可行基来启动.通过构造辅助的第一阶段问题,应用第一阶段单纯形算法可寻求初始可行基,而这一工作几乎占到整个单纯形法计算工作量的一半[1-2].相比第二阶段单纯形法,第一阶段单纯形算法能产生更多的信息,诸如目标最优值既定、人工变量都在初始基中、必须旋转出去等.如何利用这些已知信息,进一步提高第一阶段单纯形算法的计算效率,则是一个值得研究的课题. 一般地,定价分为完全定价和部分定价,完全定价需要计算所有非基变量的简约价值系数,计算代价是昂贵的.部分定价只考察非基变量的一部分,然后从中选择一个合适的候选变量入基.经典的Dantzig准则[6]、最陡边算法[7]和一些原始—对偶枢轴准则[8-9]等都属于完全定价策略,而部分定价策略包括分段定价、动态定价[3]以及嵌套定价或多重定价[4-5].显然,部分定价策略减少了对非基变量考察的计算工作量,但由于考察不全面,有可能漏掉对最佳入基变量的选择,从而增加迭代的次数.可见,部分定价策略的设计是非常灵活的,也是很讲究的,关系到计算性能的优劣. Cheng[10]发现在单纯形算法中满足某些准则的一个非基变量就会成为最优基本解中的非基变量,第一阶段单纯形法已知最优值的信息可以用于执行其中的判断准则.据此,提出了第一阶段单纯形法的一种分段定价策略,在此策略下产生两种单纯形算法变式,即首先根据Cheng的判断准则将所有非基变量分成四段,其中一段由最优基本解中的非基变量构成,再在迭代过程中对另外三段非基变量依其保持非基的可能性程度先后交替定价,并将定价后的非基变量进行相应调整.第一种算法从迭代开始就根据Cheng的两个判断准则对四段非基变量不断调整,这样用于定价的非基变量数随着迭代进程越来越少.与经典单纯形算法相比,它极大节省了定价计算的工作量,其所搜寻的非基列数之比仅为0.25,但两个判断准则的计算需要耗费大量时间,导致该算法计算效率很低.第二种算法对第一种算法作了改进,考虑到目标当前值随着迭代进程趋近最优值,越来越多的非基变量将保留在最优基中,因此,该算法选择从目标最优值的2/3处开始对非基变量分段,然后只根据Cheng的一个较简单的判断准则对定价后的非基变量进行调整,以减少判断调整的计算工作量,最后通过MATLAB编程在计算机上对来自NETLIB和MIPLIB的27个典型算例实现数值试验.结果表明改进的算法比经典单纯形算法所用的总迭代次数还少,其比为0.97,在所有算例上都比经典单纯形算法所搜寻的非基列数要少,总搜寻非基列数之比为0.65.它在所有算例上耗费的计算时间都比经典单纯形算法少,其计算性能高效而稳定. 为了更好地阐释第一阶段单纯形算法的分段定价原理,有必要重复一下Cheng的判断准则及部分证明过程. 1)B-1Aj≥0. 则xj保持为最优基本解的一个非基变量. 从而有 则意味着变量xj与最优基B*对应的简约价值系数为正,因而是最优基本解的一个非基变量. 在问题(LP1)中,改变xj的目标函数系数为cj,约束矩阵系数为Aj,就得到原来的第一阶段问题.由于其它变量的系数没有发生变化,因此xj对应最优基B*的简约价值系数仍然保持为正,即 于是,可将上述命题推广,得到如下结果. 1)B-1Aj≥0. 则xj保持为最优基本解的一个非基变量. 由于很多线性规划的现实问题都是退化的,推论1的适用性更广.除非特别声明,后面所指的条件1)、2)就是推论1的. 根据上述分析,J4确定是最优基本解中的非基变量指标集,在以后的迭代过程中不需要再定价;J2和J3中的非基变量成为最优基本解中的非基变量的可能性较大,但随着迭代进程趋近最优解,J3中的非基变量更有可能保持非基状态;J1中的非基变量成为最优基本解中的非基变量的确定性程度无法判定,应首先定价.这里采用Dantzig的“最负简约价值系数”准则来选择入基列指标.具体过程如下:选择指标集J1,每次迭代之后根据分段策略将J1中的非基变量调整到J2、J3和J4中.当J1为空时,选择J2,若J2非空时对其非基变量定价一次,调整四个指标集,再返回J1对其非基变量定价.当J1和J2都为空时,继续对J3中的非基变量定价1次,当其所有非基变量的简约价值系数保持非负,当前基本可行解就是第一阶段问题的一个最优解;否则,调整指标集J1、J2、J3和J4后,返回J1重复上述过程.基于上述算法原理,第一阶段单纯形算法分段定价策略的计算步骤描述如下: 算法A 步骤2)置J=J1,如果J为空集,转步骤3);否则,转步骤5). 步骤3)置J=J2,如果J为空集,转步骤4);否则,转步骤5). 步骤8)调整指标集J1、J2、J3和J4,返回步骤2). 为了检验算法A这种分段定价策略的计算性能,从线性规划标准测试库NETLIB[11]和混合整数规划标准测试库MIPLIB[12]中选取了27个典型算例进行初步测试(对混合整数规划问题,只求解其相应的线性规划松弛问题的解),并与经典单纯形算法的完全定价策略进行比较.使用MATLAB V7.1语言对Dantzig的经典单纯形算法和算法A进行了编程,在Lenovo ThinkCenter M9201z计算机上执行数值试验,且数值试验的环境是完全相同的.以求解线性规划问题所需要的枢轴数(用Iters表示)、定价过程中所搜寻过的非基列总数(用Cols表示)作为主要计算指标,对27个算例第一阶段问题求解.计算结果见表1. 表1 单纯形算法与分段定价策略两种算法求解第一阶段问题的计算比较 注:在获得最优表后,对退化人工变量从基中旋出,没有再给Cols计数. 从表1可以看到,算法A在11个算例上比经典单纯形算法所用的迭代次数多,在27个算例上所用的总迭代次数之比为1.17,但算法A在所有算例上所搜寻的非基列数都比经典单纯形算法少得多,总搜寻列数之比仅为0.25,即使算法A在算例scsd1上所用迭代次数之比高达2.60,所搜寻的非基列数之比也只有0.52.可见,算法A的定价效率是非常高的.然而,算法A在大部分算例上所耗费的执行时间比经典单纯形算法要多,尤其对规模较大的问题,如scagr25,lp41,mod010,其计算性能是非常差的,因而没有在表中列出算法A的执行时间.究其原因,迭代次数较多导致基矩阵求逆和基交换的计算量增加,而更重要的是算法A在每次迭代中对4个指标集的调整需要耗费大量时间,使得定价计算量的减少“得不偿失”.为此,对算法A作了进一步改进. 算法B 步骤7)置J=J1,如果J为空集,转步骤8);否则,转步骤10). 步骤8)置J=J2,如果J为空集,转步骤9);否则,转步骤10). 步骤13)按照推论1的条件1)调整指标集J1、J2、J3和J4,返回步骤7). 用MATLAB V7.1语言对算法B也进行了编程,并在Lenovo ThinkCenter M9201z计算机上求解表1中27个算例的第一阶段问题(计算结果见表1). 从表1可见,改进的算法B虽然比算法A大幅增加了定价所搜寻的非基列数,但却减少了迭代的次数,即与经典单纯形算法所用的总迭代次数之比为0.97,且在23个算例上比经典单纯形算法所用的迭代次数要少或相同.由于在所有算例上都比经典单纯形算法所搜寻的非基列数要少,因而其计算时间也比经典单纯形算法耗费得少,其计算性能高效而稳定. 单纯形算法的计算工作量主要取决于迭代的次数和所搜寻的非基列数,部分定价策略就是在每次迭代中设法减少对非基变量的定价.本算法把所有非基变量按照它们成为最优解中的非基变量的确定性程度分成四段,然后按可能性从小到大的顺序选择一段非基变量进行定价,且每次迭代还要根据分段准则对四段非基变量实施动态调整.随着迭代进程趋于最优解,不需要定价的非基变量数越来越多,因而所提出的分段定价策略可大大节省对非基变量定价的计算工作量. 分段调整的过程也需要耗费计算时间,如果调整计算太复杂,调整时机不合适,就会造成“得不偿失”的结果,算法A就验证了这一点.有时“简单的就是最好的”,大量数值试验已经验证了经典单纯形算法的高效性,为此算法B改进了算法A的缺陷.考虑到单纯形算法在目标值接近最优值时迭代非常缓慢,此时大部分非基变量都保持非基不变.于是,根据经验选择了一个适当的分段时机,同时摒弃复杂的调整准则.初步计算结果表明,这种改进是有效的,尤其对较大规模的问题,其计算优越性体现得更加明显. [1] 李炜.求线性规划初始可行基的新方法[J].运筹与管理,2004,13(1):7-10. [2] 高培旺.关于求线性规划初始正则解的一个新方法的注记[J].徐州工程学院学报(自然科学版),2012,27(2):1-4. [3] MAROS I.A general pricing scheme for the simplex method[J].Annals of Operations Research,2003,124(1):193-203. [4] PAN P Q,LI W,CAO J.Partial pricing rule simplex method with deficient basis[J].Numerical Mathematics:A Journal of Chinese Universities,2006,15(1):23-30. [5] PAN P Q.Efficient nested pricing in the simplex algorithm[J].Operations Research Letters,2008,36(3):309-313. [6] 束金龙,闻人凯.线性规划理论与模型应用[M].北京:科学出版社,2013. [7] FORRESTJ J H,GOLDFARB D.Steepest-edge simplex algorithm for linear programming[J].Mathematical Programming,1992,57(3):341-374. [8] CURET N D.A primal-dual simplex method for linear programs[J].Operations Research Letters,1993,13(4):233-237. [9] CHEN H D,PARDALOS P M,SAUNDERS M A.The simplex algorithm with a new primal and dual pivot rule[J].Operations Research Letters,1994,16(3):121-127. [10] CHENG M C.New criteria for the simplex algorithm[J].Mathematical Programming,1980,19(2):230-236. [11] DONGARRA J,GOLUB G,GROSSEE,et al.Netlib and NA-Net:building a scientific computing community[J].IEEE Annals of the history of computing,2008,30(2):30-41. [12] BIXBY R E,CERIA S,MCZEAL C M,et al.An updated mixed integer programming library:MIPLIB 3.0[J].Optima,1998,54(1):12-15. (编辑 徐永铭) A Sectional Pricing Strategy for the Phase-1 Simplex Method GAO Peiwang (Minjiang University, Fuzhou 350121, China) The paper presents a sectional pricing strategy for the phase-1 simplex algorithm.Based on this,two variants are derived.Firstly,all nonbasic variables are partitioned into four sections,one of which includes the nonbasic variables in an optimal solution.In the iterative process,pricing is implemented alternatively in turns in other three sections according to the possibility of those variables remaining nonbasis.Variant 1 uses Cheng's two criteria to change the composition of components in four sections at the outset of the iteration.So it greatly decreases the amount of pricing computation,but spends much more time than the classical simplex algorithm.Variant 2 starts section when the objective value arrives at two third of the optimum value,and changes sections by only one of Cheng's criteria.A preliminary test is accomplished on a set of 27 standard instances from NETLIB and MIPLIB.The computational results show that variant 2 uses fewer iterations in total, probes fewer columns,and spend much less computational time than the classical simplex algorithm.Therefore, variant 2 is of the interest in computational performance. linear programming; simplex method; pricing rule; sectional pricing; computational efficiency 2016-06-02 闽江学院人才引进基金资助课题(MJU2012001);广西自然科学基金项目(0728260);国家星火计划项目(2013GA690426) 高培旺(1964-),男,教授,博士,硕士生导师,主要从事最优化理论及其应用研究. O221.1 A 1674-358X(2016)04-0021-06
1 第一阶段单纯形算法的分段定价原理
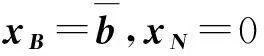
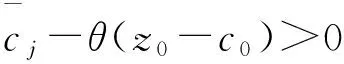
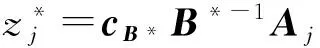
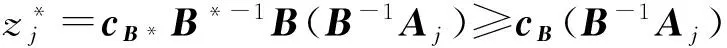
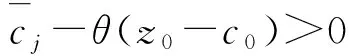
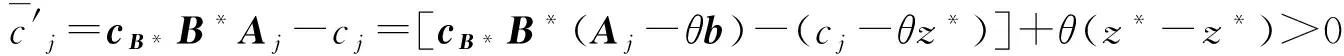
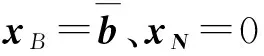
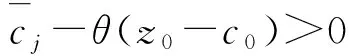
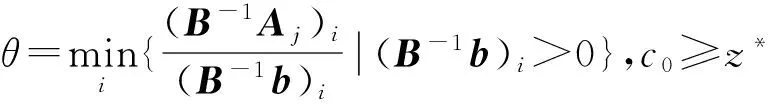
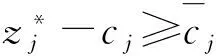
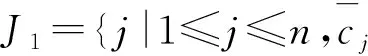
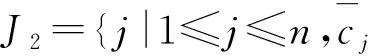
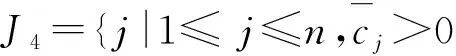
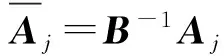
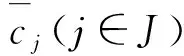
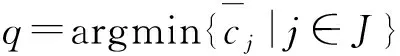
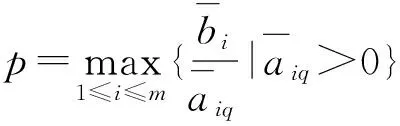
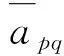

2 进一步改进
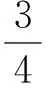
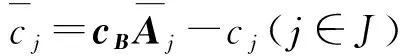
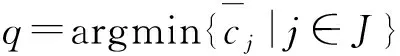
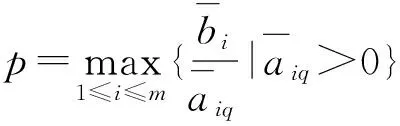
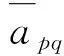
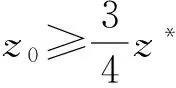
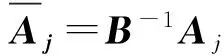
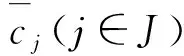
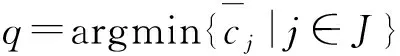
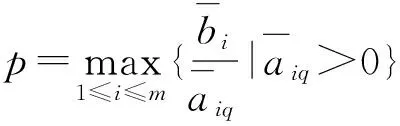
3 结论
