单参数Lorenz混沌系统及其保密通信

李泽彬，张 刚，李 宣，朱雪梅

(皖西学院，安徽 六安 237012)

单参数Lorenz混沌系统及其保密通信

李泽彬，张 刚，李 宣，朱雪梅

(皖西学院，安徽 六安 237012)

为优化单参数Lorenz混沌系统在保密通信中的应用，在时间尺度变换的基础上，设计新的混沌电路系统;利用PC同步控制方案实现该混沌系统构成的驱动电路和响应电路的同步，并将其应用于保密通信.仿真实验结果表明该保密通信系统能够有效地掩盖和恢复出有用信号，具有良好的保密性.

混沌系统；混沌同步；保密通信

混沌科学是20世纪晚期形成的综合性科学分支，是继相对论和量子力学之后，又一具有革命性的重大科学进展[1-2].自1963年美国著名的气象学家Lorenz[3]提出Lorenz方程以来，掀起了对混沌系统及其在各领域中应用的热潮[4-7].由于混沌系统产生的混沌信号具有类随机性、连续宽带频谱、类噪声等特点，很适合用于信息加密和保密通信等领域[8-9].将混沌应用于保密通信的一个关键问题就是混沌系统的同步与控制，然而当前混沌系统的同步与控制方案[10-13]很多，大多学者研究的同步与控制方案比较复杂，需要较长时间才能达到混沌同步，给即时保密通信带来了不便.另外，大多数混沌系统的带宽较低，不能够完全掩盖高频率的有用信号[14]，限制了混沌系统的应用.为此，采用时间尺度变换提高混沌系统带宽，以求为有效掩盖更高频率的有用信号提供支持.同时，采用PC同步控制方案，设计单变量Lorenz系统同步电路，将其应用于保密通信，达到了较好的保密效果.

1 混沌系统

1.1 数学模型

采用王光义等[15]提出的单参数三维二次混沌系统，即

(1)

那么，为了便于LabVIEW编程计算，将系统(1)变形为方程

(2)

式中b=3.4时，初始值(x0，y0，z0)为(-0.1，0.1，-0.1).取dt=0.005，对方程(2)进行前面板设计和后面板的程序框图设计，运行计算后可通过虚拟仪器得到时序图和相图.如图1所示.

由图1中x、y和z的时序图可知，时域波形表现出非周期、不可预测性；从图1中x-y、y-z和x-z的相图可知，该系统存在混沌吸引子，即系统在上述参数作用下处于混沌状态，而这一结果与文献[15]一致.

图1 混沌系统的时序图和相图

1.2 电路设计与仿真

从图1时序图可以看出，系统(1)产生的混沌信号频率较小，不利于其具体应用，因此对系统(1)进行时间尺度变换.令t=1000τ，则

(3)

那么，为了便于电路设计，将系统(3)进行数学变换，得方程

(4)

式中C1、C2为积分常数，取初始时值为0时，则C1、C2为0.然后根据方程(4)，利用模拟运算放大器、模拟乘法器、电阻、电容，得到混沌电路系统.如图2所示.对图2系统电路进行Multisim仿真，得到相图.如图3所示.从图3可知得到的相图和LabVIEW编程计算结果一致，从而证实该电路设计是正确的.

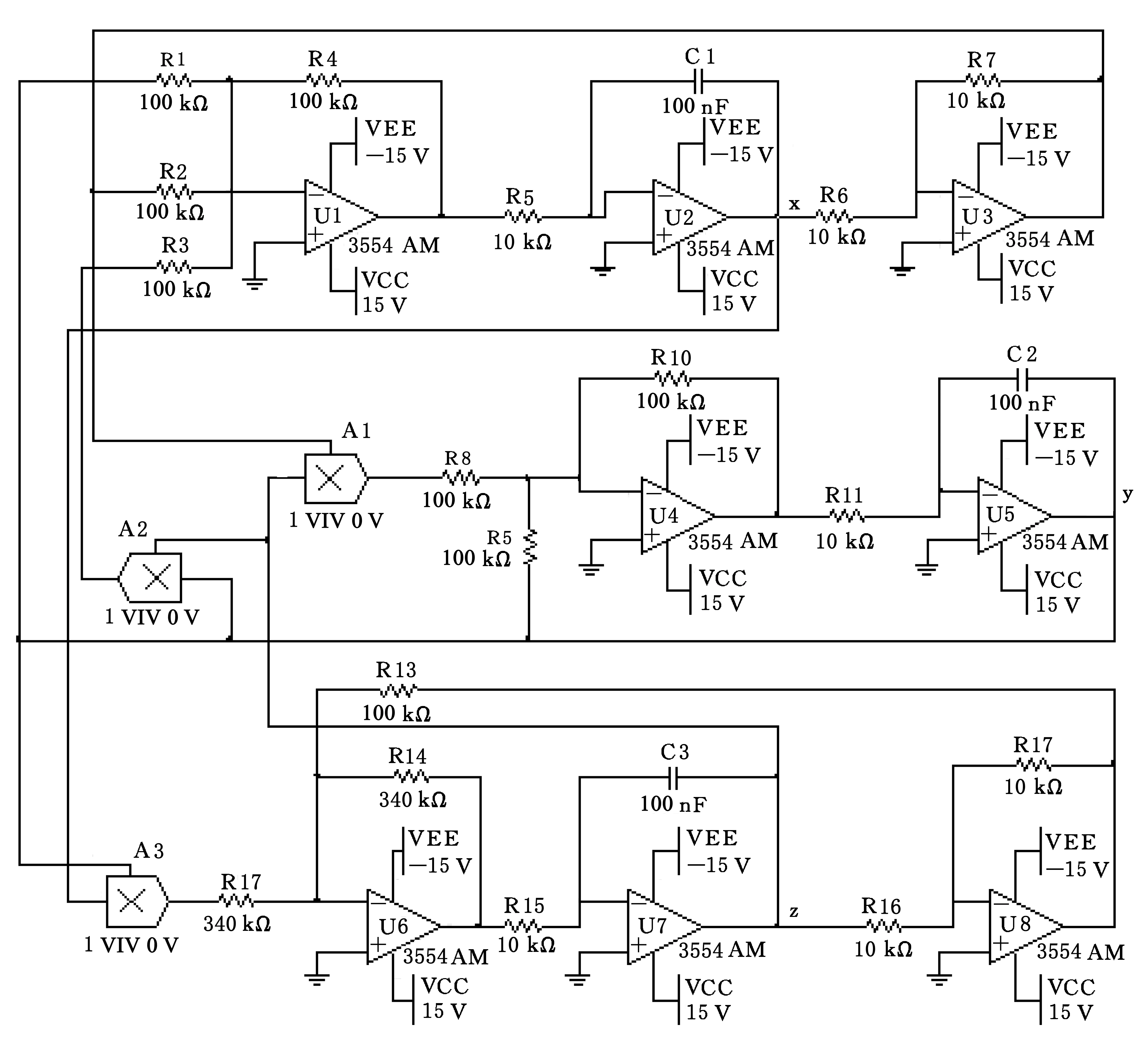
图2 混沌电路系统

图3 混沌电路系统的相图

2 保密通信系统设计与仿真

2.1 混沌同步系统设计

混沌同步是混沌保密通信技术的基础，故而采用PC同步控制方案[16].该方案是用1个混沌系统的状态驱动另一个混沌系统来实现2个混沌系统的同步，且驱动系统不会受到响应系统的影响，而响应系统的动力学行为完全由驱动系统来决定.采用y1作为驱动变量，其驱动系统和响应系统状态方程分别为

(5)

(6)

设计的同步电路系统如图4所示.对其进行仿真，其结果如图5所示.由图5可知，驱动电路x(t)、z(t)和响应电路x1(t)、z1(t)可以分别达到同步，而这为进一步实现混沌保密通信奠定了基础.

图4 Lorenz混沌同步电路

2.2 混沌保密电路设计与仿真

基于Lorenz混沌同步电路，利用反相求和电路U15、反相比例运算电路U16和减法电路U17，实现了保密通信电路.如图6所示，U15构成信号发送端，将驱动系统产生x(t)混沌信号和发送信号s(t)调制成混合信号；U16将混合信号进行反相形成传输信号m(t)；U17将接收到的传输信号m(t)减去响应系统产生的x1(t)混沌信号，实现信号的解调，并将发送信号还原出来.将频率50 Hz、幅度500 mV方波信号和正弦信号分别加载到保密通信电路中，仿真出来的结果如图7所示.由图7可以看出传输信号m(t)具有随机、无规则特点，发送信号被完全掩盖在混沌信号中，使得传输信号难以被破解；其发送信号和解调出来的信号完全一致，即信号s(t)与信号s＇(t)一致，实现了信号的加密和解密.在实验中，发现频率很高的信号很难被本参数系统产生的混沌信号所掩盖，但通过时间尺度变换可使系统提高混沌信号的频率，从而较好解决了高频信号的保密通信.但是，大幅度信号受到电路本身器件和工作电压限制，很难利用该混沌信号实现保密.

图5 混沌系统的同步效果

图6 Lorenz混沌保密通信电路

图7 混沌保密通信过程中的信号

3 结语

针对单参数Lorenz混沌系统，采用LabVIEW编程计算证实了该系统具有混沌特性，推导设计了变尺度混沌系统，解决了系统输出混沌信号频率较低问题，并利用该系统设计了混沌电路；利用PC同步控制方案设计了混沌同步电路，并将该结果应用于混沌保密通信；通过保密通信电路系统仿真得到该电路系统能够较好地实现基本信号的保密通信，而对于频率很高的信号需要改进系统才能实现信号保密；大幅度信号由于电路本身器件和工作电压的限制，使得保密效果较差.

[1] 郑会永,肖田元.混沌及混沌保密通讯技术[J].中国图象图形学报,1998(12):1042-1050.

[2] 杨芷萱.复杂网络动力学的理论研究及其在博弈论中的应用[D].大连:大连理工大学,2010.

[3] LORENZ E N.Deterministic nonperiodic flow[J].Journal of the Atmospheric Sciences,1963,20(2):130-141.

[4] 陈广甸,荣识广,麦文昌,等.Lorenz混沌电路的改进及实现[J].湖南科技大学学报(自然科学版),2015(4):111-116.

[5] 李国辉,徐得名,周世.Lorenz混沌系统的跟踪控制[J].量子电子学报,2003,20(2):181-185.

[6] 张错玲,韦良芬.基于Lorenz超混沌理论的数字图像加密算法研究[J].湖北大学学报(自然科学版),2016,38(6):551.

[7] 何晔,王磊,夏晖,等.基于三维Lorenz混沌的彩色视频加密[J].计算机科学,2013,40(s1):365-367.

[8] 兀旦晖,赵晨飞,张玉杰,等.时分复用在混沌保密通信中的应用研究[J].计算机测量与控制,2008,16(12):1957-1959.

[9] 浦晨岚,李为相,林锦国,等.一种混沌同步系统及其在保密通信中的应用[J].科技通报,2006,22(6):841-845.

[10] PECORA L M,CARROLL T L,JOHNSON G A,et al.Synchronization in chaotic systems[J].Chaos an Interdisciplinary Journal of Nonlinear Science,2015,64(9):821-824.

[11] 刘杰,陈士华,陆君安.统一混沌系统的投影同步与控制[J].物理学报,2003,52(7):1595-1599.

[12] 王宇野,许红珍,郭黎利.反步自适应方法实现混沌系统的同步[J].计算机仿真,2010,27(2):175-179.

[13] 邵书义,陈谋,SHAO S Y,等.一类分数阶非线性混沌系统的同步控制[J].计算机仿真,2015,32(4):394-398.

[14] 郝建红,吴淑花.Liu混沌加密系统的抗干扰分析[J].河北师范大学学报(自然科学版),2010,34(4):411-416.

[15] 王光义,丘水生,陈辉,等.一个新的混沌系统及其电路设计与实现[J].电路与系统学报,2008,13(5):58-60.

[16] 沐晶晶.超混沌系统及其在通讯保密方面的应用[D].天津科技大学,2011.

(编辑 徐永铭)

Single Parameter Lorenz Chaos System and Its Secure Communication

LI Zebin, ZHANG Gang, LI Xuan, ZHU Xuemei

(Comprehensive Application Laboratory of Sensor Networks and Information Processing System,West Anhui University, Lu'an 237012, China)

In order to optimize the application of single-parameter Lorenz chaotic system in secure communication,a novel chaotic circuit system is designed based on time-scale transformation.Synchronization of the driving circuit and response circuit is realized by using PC synchronization control scheme and is applied to secure communication.The simulation results show that the proposed method can effectively conceal and recover useful signals, and has good security.

chaos system; chaotic synchronization; secure communication

2016-09-14

安徽高校省级自然科学研究项目(KJ103762015B20)；省级大学生创新创业训练计划项目( AH201510376017 ，AH201510376034)；皖西学院校级科学研究项目(WXZR201642)

李泽彬(1979-)，男，讲师，硕士，主要从事复杂系统、混沌信号处理和机器人技术等研究.

TP391

A

1674-358X(2016)04-0070-06