基于非线性PLSR模型的气候变化对粮食产量的影响分析*

陈纪波，胡 慧，陈克垚，王桂芝

（1.南京信息工程大学数学与统计学院，南京 210044; 2.中国气象局国家气候中心，北京 100081）

基于非线性PLSR模型的气候变化对粮食产量的影响分析*

陈纪波1，胡 慧1，陈克垚2**，王桂芝1

（1.南京信息工程大学数学与统计学院，南京 210044; 2.中国气象局国家气候中心，北京 100081）

考虑气候因子间多重共线性及其与粮食产量间复杂的非线性关系，本文在HP滤波分离出气候产量的基础上，尝试引入基于三次 B样条变换（Spline-PLSR）和内部嵌入 GRNN的两种非线性偏最小二乘模型（GRNN-PLSR），利用1961-2008年气候因子数据建立气候产量计算模型，以2009—2013年数据进行拟合检验，并与常用的C-D生产函数法计算的气候产量进行比较。结果表明，Spline-PLSR法在拟合气候因子变化对粮食产量影响时预测精度较高。而且，与 C-D生产函数法相比，Spline-PLSR所需要素较少，操作简单，相对误差最高仅为13.6%；与GRNN-PLSR法拟合结果相比，Spline-PLSR相对误差波动较小，因此，基于三次B样条变换的非线性偏最小二乘法建模较适合拟合气候产量。

气候产量；偏最小二乘法；三次B样条；广义回归神经网络

20世纪80年代以来，中国土地开垦逐渐饱和，物质增产的作用日趋稳定，加之社会技术水平渐趋成熟，因此，社会物质因素对粮食产量的影响也趋于稳定[1]；而近年来，粮食主产区黄淮海平原和东北平原由于气温不断上升、水资源短缺造成干旱严重，气候因素对粮食产量的影响日渐变大[2]。因此，在气候变化的大趋势情境下，如何适应气候变化成为确保粮食增产的新兴挑战[3]。

目前，在气候因子变化与粮食产量关系研究中运用的统计学方法主要有逐步多元回归、积分回归以及EOF等，Pirjo[4]利用逐步多元回归探讨了3个不同的生长阶段气候因素对燕麦产量的影响。何永坤等[5]利用积分回归方法分析了气候波动对三峡库区主要粮食作物小麦、玉米、中稻产量的影响。Xie等[6]利用EOF法研究中国1949-1992年的粮食单产数据，结果表明中国东部地区粮食产量波动比西部地区高，气候变化收益率存在地域上的差异性。杨文坎等[7]利用 EOF等数理统计方法分析了气候变化对越南北方水稻生产的影响。但上述方法不能将气候因子与农业因子之间复杂的生态关系进行阐述，在建模过程中还存在气候因子之间存在较强的多重共线性，以及气候因子与粮食产量之间存在非常复杂的非线性关系等问题。业界提出的解决共线性的方法有岭估计、主成分估计及压缩估计等，但此类方法均存在不同程度的缺陷[8]。而偏最小二乘估计（PLSR）可以有效解决多重共线性问题。但普通的PLSR模型适用于存在线性关系的变量之间，而对于气候因子与粮食产量这种复杂的非线性关系，则需引入非线性PLSR模型。

近年来，研究者在PLSR的基础上发展了非线性偏最小二乘方法[9]。这些方法大体分为两类：一是基于外部样本变换的方法，即对自变量矩阵进行适当的变换，将原变量间的非线性关系转化为拟线性关系，再利用PLSR方法进行处理。另一类是基于内部成分间非线性映射的方法，其是先从原始的自变量和因变量中提取各自的成分，再通过对成分进行内部的非线性映射来完成非线性建模[10]，其常用的内部非线性映射有支持向量机映射[11]、神经网络映射等。其中对于样条函数变换的PLSR和内部神经网络映射的PLSR的应用较为广泛和深入，因此，本文在利用HP滤波分离出气候产量的基础上[12]，尝试引入基于三次B样条变换和内部嵌入 GRNN的两种非线性偏最小二乘模型对1961-2008年的气候因子与气候产量关系进行拟合，再用2009-2013年气候产量进行检验，并与常用的C-D生产方法进行比较，从而为研究气候因子变化对粮食产量的影响提供新思路。

1 资料与方法

1.1 资料来源及处理

对中国粮食产量问题的研究可以从粮食总产和单产两方面入手，两者的区别在于是否考虑粮食作物实际占用的耕地面积。中国粮食总产量的持续增长很大程度上由粮食单产的大幅提高所致，而非粮食作物实际占用的耕地面积的增加[13]。基于上述考虑，本文选取世界银行数据网站（http：//data.worldbank.org.cn/）公布的1961-2013年中国粮食单产数据进行分析。气候因子选取 1961-2013年平均温度、降水量及日照时数。

研究选用样条函数变换的 PLSR和内部神经网络映射的PLSR方法，以1961-2008年气候产量作为模拟训练数据建模，用 2009-2013年气候产量进行模型检验。

1.2 三次B样条理论

样条函数由Schoenberg于1946年首次提出，现已广泛应用于各个领域。考虑到B样条在局部敏感的特性，实际应用中经常采用B样条基函数即关于y轴对称的且在（-2，2）内取值非零的函数。本文采用的三次B样条可表示为

式中，下标+代表正整数。

1.3 广义回归神经网络理论

GRNN具有很强的非线性映射能力，在逼近能力和学习速度上具有较强的优势，适用于解决非线性问题[14]。GRNN的理论基础是非线性回归，设随机变量x和y的联合概率密度函数为f（x，y），已知x的观测值为X，则y相对于X的回归，即条件均值为

对于未知的概率密度函数 f（x，y），可以由 x和y的样本观测值估计得到，其非参数估计为

式中，Xi、Yi为随机变量x和y的样本观测值；σ为平滑参数（即核宽度）；n为样本数目；m为随机变量x的维数。

1.4 C-D生产函数

C-D生产函数主要用于农业生产过程中要素投入对产出贡献大小的经济分析中。目前常用的 C-D生产函数模型一般表达式为

式中，Y为产出量，x1、x2、x3分别为土地、劳动力和资金投入量，b1、b2、b3分别是土地、劳动力和资金的生产弹性值，表示一定的土地、劳动力和资金投入的变化率所引起的产出量的变化率。a是转换系数，它表示除x1、x2、x3之外的其它生产要素对产出量的影响。目前C-D生产函数在应用中一般会线性化，对上式两边取对数得到，即

2 结果与分析

2.1 基于HP滤波的气候产量分离

本文直接使用文献[12]中的HP滤波进行趋势产量和气候产量的分离，得到图 1所示的气候产量分离结果，由图可见，气候产量曲线呈明显的波动态势，说明气候变化对粮食产量的影响时正时负，而曲线波动的范围反映了气候变化对粮食产量贡献率的大小。

图1 粮食产量实际值与HP滤波法趋势产量、气候产量分离值的变化过程（1961-2014）Fig.1 The actual yield and trend yield separated and climatic yield by HP filter in 1961-2014

2.2 构建基于三次B样条变换的非线性PLSR模型

2.2.1 气候因子间的多重共线性检验

根据经验法则，若模型中两个自变量的相关系数的绝对值超过 0.7，则可以判定多重共线性会成为模型的潜在问题[15]。因此，为确保模型的精确度，须对气候因子之间的多重共线性进行检验。采用SPSS对气候因子进行多重共线性诊断，诊断结果如表1。

表1 气候因子间的多重共线性诊断表Table 1 The multi-collinearity diagnostics table among climatic factors

由表1可知，通过0.01的显著性检验且具有较大相关性的变量有温度和日照时数，其 Pearson相关系数高达0.8692，远超于0.7，因此，本文认为温度和日照时数的多重共线性会影响普通回归模型的精度。

2.2.2 基于三次B样条变换的非线性PLSR模型

对原自变量进行非线性变换处理，也即将自变量系统的每一维xj进行三次B样条转换具体计算分4个步骤。

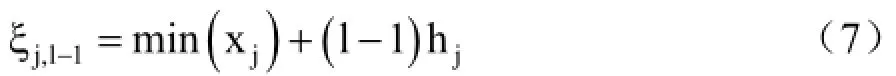
式中，三次B样条基函数

则

从而得到新的数据满足的线性关系为

（4）对式（12）进行偏最小二乘回归建模[10]，求出具体的回归系数。再将标准化处理的算式及回归系数和样条函数变换式代入，最终得到y关于X的非线性回归模型为

本文以气候产量为因变量（y），气候因子温度（x1）、降水量（x2）和日照时数（x3）为自变量，选取1961-2008年产量为训练用数据。根据上述建模步骤（7）-（13），将数据经过相应的标准化处理后，运用matlab软件编程。求得最佳为7，成分数为17，而和的值由于数据较大，因此本文在此省略，故求得最终回归系数值为

得到最终模型为

通过上述模型拟合的 1961-2005年的气候产量数据与实际HP分离出的气候产量数据对比见图2。由图2可见，整体上基于三次B样条变换的非线性PLSR模型在气候产量上的拟合较好，但在 1977、1980和1981年存在较大差异。

2.3 构建神经网络内部嵌入的非线性PLSR模型

通过在传统的偏最小二乘方法框架内部嵌入GRNN模型，对成分进行非线性映射。这种思路将PLSR方法与GRNN模型相结合，利用PLSR外部投影作用来去除共线性，GRNN模型在内部获得投影空间中的非线性映射关系，基本原理如图3。

结合图3，GRNN-PLSR模型是先令主成分数初值h=1，利用PLSR求出外部关系。再利用GRNN模型建立内部关系函数fh（·），求解内部关系uh= f（th）。主要利用四层的 GRNN网络求解输入输出的映射关系。先将样本分成训练样本和测试样本，再对测试样本求取和即

图2 Spline-PLSR气候产量预测值与实际值的比较（1961-2005）Fig.2 The actual climatic yield separated by HP filter and the climatic yield predicted by Spline-PLSR in 1961-2005

然后，计算自变量和因变量的载荷向量。

最终通过交叉验证决定主成分的个数：即若上述建立的GRNN输入输出模型不满足所需要的精度时，令h h1= +，再重新计算。否则结束。

选取 1961-2008年为训练用数据，根据上述步骤，利用matlab软件进行编程，求得最终提取的成分数为h=3，运用GRNN建立内部非线性关系时，求得最佳spread值为0.1。最终得到GRNN-PLSR模拟得出的1961-2008年的气候产量数据与实际HP分离出的气候产量数据对比见图4，由图4可见，整体上基于GRNN模型内嵌的非线性PLSR模型在气候产量的预测中波动较大，在 1977、1986以及 2004年存在较大的误差。

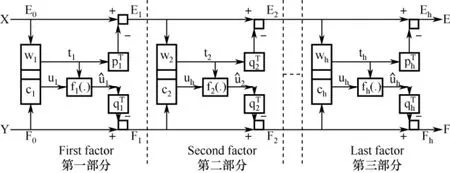
图3 GRNN-PLSR运行基本原理图Fig.3 The operating mechanism figure of GRNN

图 4 GRNN-PLSR气候产量预测值与实际值的比较（1961-2008）Fig.4 The actual climatic yield separated by HP filter and the climatic yield predicted by GRNN-PLSR in 1961-2008

2.3 Spline-PLSR模型、GRNN-PLSR模型与C-D生产函数精度比较

2.3.1 C-D生产函数

文献[16]运用C-D生产函数对气候因子与粮食产量的关系进行了研究，认为影响中国粮食产量的三大要素为技术进步、土地利用和水资源。本文在考虑数据可获得性的基础上，以这三大要素为基础，拟定生产函数所需的两大指标为气候指标和物质投入指标。其中物质投入指标分别有播种面积比重、农业机械化、化肥施用量、有效灌溉面积比重及劳动力共5项，气候指标为气温、降水量和日照时数。具体指标体系见表2。

表2 C-D生产函数所需指标体系Table 2 The index table in C-D production functions

将1978-2008年所有指标取对数后建模得到

式中，Y为历年粮食实际产量（kg·hm-2），为待估系数，T表示技术进步（1978-2008年共31个技术进步值），X表示物质投入因素，C表示气候因素，下标t表示年份，ε表示随机误差。由于自变量间存在多重共线性，因此，在C-D生产函数拟合过程中采用岭回归估计方法。使用SAS编程得到，岭参数k为0.1，其系数分别为

用式（19）对实际粮食单产进行建模后，再利用分离出的趋势产量，计算C-D生产函数模拟出的气候产量。

表3 三种模型对2009-2013年气候产量预测值和相对误差的对比Table 3 Compare of the predicted climatic yield and its relative error by three methods in 2009-2013

2.3.2 预测精度比较

为考察所构建非线性PLSR模型的精确度，分别采用PLSR法、GRNN-PLSR法以及C-D生产函数法对2009-2013年的气候产量数据进行拟合，并与HP滤波分离出的气候产量数值进行对比计算相对误差，结果见表3。由表3可见，采用C-D生产函数模型预测时，结果参差不齐，相对误差较大，误差绝对值在2013年达到75.85%，这是由于C-D生产函数是线性回归，其呈现不断变大的过程，不能体现自变量与因变量间的非线性。而采用本文建立的Spline-PLSR以及 GRNN-PLSR法拟合的模型在预测中误差相对小得多。但GRNN-PLSR法的相对误差较样条变换的非线性PLSR相对误差大，这是因为神经网络在拟合中较好，但在预测时存在过拟合的问题，因此导致预测时误差相对Spline-PLSR方法较大。

3 结论与讨论

3.1 讨论

以往研究长时间序列的气候因子变化与粮食产量关系，多采用逐步回归分析、C-D生产函数法以及EOF法，其中以C-D生产函数法应用较为广泛。但上述方法存在一定的不足。刘春琼等[16]采用去趋势互相关分析（DCCA）对四川省1961-2012年气温、降水距平值与粮食产量的相关性及其随时间序列的变化进行分析，但其只能分析出两者之间存在正相关还是负相关，对两者具体的定量关系不能给出计算，且不能对未来气候变化对粮食产量的影响进行预测。目前还未见将非线性的PLSR模型运用其中的报道，本文就此进行了一个新的尝试。由于气候因子间存在多重共线性且其与粮食产量是非线性关系，因此考虑引入非线性PLSR模型进行建模。又考虑到非线性PLSR模型存在两种构建途径，一是将自变量因子通过函数变换成拟线性从而构造非线性PLSR模型；二是对普通PLSR模型的内部线性关系进行非线性模型替换从而达到非线性效果。因此，本文选用基于三次B样条变换的非线性偏最小二乘以及内部嵌入GRNN模型的非线性偏最小二乘模型进行建模。有关非线性偏最小二乘方法的分析结果表明，气候变化对粮食产量正影响最大值出现在1985年，负影响最大值出现在1977年，且本文的研究成果能够用于在未来A2、B2情境下对粮食产量进行预测。但本文仅用了常用的将线性PLSR模型转换为非线性PLSR的两种方法，在未来研究中可以深入研究其余内嵌非线性模型进行转换的方法，从而达到更好的预测效果。

3.2 结论

（1）两种非线性PLSR模型与常用的C-D生产函数法的拟合结果的比较表明，非线性PLSR模型的总体拟合效果及预测精度均高于C-D生产函数法，这是由于C-D生产函数考虑要素过多，容易造成模糊重点等可能性发生；而非线性PLSR模型所需分析的要素较少，计算更为方便快速，因此，最终模型预测精度较高。

（2）GRNN-PLSR法和三次B样条变换的非线性PLSR法所建模型的拟合结果的比较表明，前者相对误差较后者要大，这是由于神经网络在拟合中较好，但在预测时存在过拟合的问题，因此，导致预测时误差相对Spline-PLSR方法较大。

可见，基于三次B样条变换的非线性偏最小二乘模型以及嵌入GRNN构造的非线性偏最小二乘模型，均能用于气候变化与粮食产量间的关系分析建模中。实证结果表明，应用基于三次B样条变换的非线性偏最小二乘法在拟合气候因子对粮食产量影响变化时简单方便，预测精度更高，可以满足实际应用需求。同常用的 C-D生产函数模型相比，Spline-PLSR更为有效分析要素间的非线性关系，具有较高精度；与通过嵌入GRNN构造的非线性PLSR相比，Spline-PLSR模型具有更高的稳定性，不存在过拟合以及随机性的状况。

References

[1]陆金帅.气候因子变化对我国粮食产量的影响及关系研究[D].南京：南京信息工程大学,2014.Lu J S.Research on the relationship of climatic factors and grain yield in China[D].Nanjing：Nanjing University of Information Science and Technology,2014.(in Chinese)

[2]周文魁.气候变化对中国粮食生产的影响及应对策略[D].南京：南京农业大学,2012.Zhou W K.Impact of climate change impact on Chinese food production and its countermeasures[D].Nanjing：Nanjing Agricultural University,2012.(in Chinese)

[3]李琳凤.我国粮食产业安全问题研究[D].北京：北京交通大学,2013.Li L F.Research on China's grain industrial security[D].Beijing：Beijing Jiaotong University,2013.(in Chinese)

[4]Pirjo P.Effect of climatic factors on the yield and on the characteristics connected to yielding ability of oats(Avena sativa L)[J].Acta Agriculturae Scandinavica,1990,40(1)：23-31.

[5]何永坤,王裕文.重庆市三峡库区气候变化对粮食产量的影响分析[J].山区开发,2001,(12)：36-39.He Y K,Wang Y W.The analysis of the impact of climate change on food production in the three gorges of Chongqing[J].Mountain Development, 2001,(12)：36-39.(in Chinese)

[6]Xie Y,Liu J D.Impact of climate on grain yield per unit area inChina during the years of 1949-1992[J].Chinese Geographical Science,1998, 84(6)：309-316.

[7]杨文坎,李湘阁.气候变化对越南北方水稻生产的影响[J].南京气象学院学报,2004,(1)：55-64.Yang W K,Li X G.Climatic change and its effect on rice yields in the north Vietnam[J].Journal of Nanjing Institute of Meteorology,2004,(1)：55-64.(in Chinese)

[8]程娟.稳健主成分估计的性质及在多因素定价模型中的应用[D].重庆：重庆大学,2006.Cheng J.Properties of robust primary component estimation and utilization in Multi-Fact Pricing Model[D].Chongqing：Chongqing University,2006.(in Chinese)

[9]朱卫华.人体血清光谱特性分析与建模研究[D].南京：南京航空航天大学,2012.Zhu W H.Characteristic analysis and modeling study on human serum spectrum[D].Nanjing：Nanjing University of Aeronautics and Astronautics,2012.(in Chinese)

[10]郝健,刘俊民,张殷钦.基于非线性PLSR模型的地下水水质预测[J].西北农林科技大学学报（自然科学版）,2011,（7）：212-216.Hao J,Liu J M,Zhang Y Q.Prediction of groundwater quality based on nonlinear PLSR model[J].Journal of Northwest A &F University (Nat.Sci.Ed.),2011,(7)：212-216.(in Chinese)

[11]Gu B,Sheng V S,Wang Z J,et al.Incremental learning for ν-Support Vector Regression[J].Neural Networks,2015,67：140-150.

[12]王桂芝,陆金帅,陈克垚,等.基于HP滤波的气候产量分离方法探讨[J].中国农业气象,2014,35（2）：195-199.Wang G Z,Lu J S,Chen K Y,et al.Exploration of method in separating climatic output based on HP Filter[J].Chinese Journal of Agrometeorology, 2014,35(2)：195-199.(in Chinese)

[13]王桂芝,胡慧,陈纪波,等.基于BP滤波的Fourier模型在粮食产量预测中的应用[J].中国农业气象,2015,36（4）：472-478.Wang G Z,Hu H,Chen J B,et al.Application of Fourier model based on BP filter in grain yield prediction[J].Chinese Journal of Agrometeorology,2015,36(4)：472-478.(in Chinese)

[14]王雪冬,董慧.基于广义回归神经网络的矿井涌水量预测[J].中国安全生产科学技术,2014,（11）：90-93.Wang X D,Dong H.Prediction of water yield in mine based on generalized regression neural network[J].Journal of Safety Science and Technology,2014,(11)：90-93.(in Chinese)

[15]程远,丁书萍,程卉,等.黑龙江省水稻种植产量与气候因子的关系[J].中国农学通报,2012,（18）：98-101.Cheng Y,Ding S P,Cheng H,et al.The relationship between rice yield and climate factors of Heilongjiang province[J].Chinese Agricultural Science Bulletin,2012, (18)：98-101.(in Chinese)

[16]刘春琼,刘萍,吴生虎,等.基于DCCA方法分析气候变化对四川省粮食产量的影响[J].中国农业气象,2016,35（1）：43-50.Liu C Q,Liu P,Wu S H,et al.Impacts of Climate change on grain output in Sichuan based on the detrended cross-correlation analysis method[J].Chinese Journal of Agrometeorology, 2016,35(1)：43-50.(in Chinese)

Effects of Climate Change on the Grain Yield Based on Nonlinear PLSR Model

CHEN Ji-bo1，HU Hui1，CHEN Ke-yao2，WANG Gui-zhi1
（1.School of Mathematics and Statistics, Nanjing University of Information Science and Technology，Nanjing 210044, China; 2.National Climate Center, China Meteorological Administration, Beijing 100081）

Considering the multicollinearity of climatic factors，as well as the complex nonlinear relationship between climatic factors and the grain yield, authors attempt to model the climatic factors and climate yield data from 1961 and 2008 in this paper with respect to the cubic B splines function（Spline-PLSR）and internal embedded Generalized regression neural network（GRNN）into the partial least squares regression，on the basis of separating the climatic yield by HP filter.Through the fitting test based on the data from 2009 to 2013 and the comparison between the C-D production function and the proposed model，authors determine that the Spline-PLSR model is relatively simple with higher prediction accuracy.Compared with the C-D production function，the Spline-PLSR model requires fewer elements and possesses a better forecasting value.It is worth noting that the fitting result of Spline-PLSR is more stable than that of GRNN-PLSR.Hence，it is a better choice to utilize Spline-PLSR to fit the influence of climatic factors on the grain yield.

Climatic yield; Partial least squares regression; Cubic B-spline; Generalized regression neural network.

2016-03-20**

国家社会科学基金(15BTJ019)

陈纪波（1961-），副教授，研究方向为应用统计。E-mail：chenjibo@nuist.edu.cn

10.3969/j.issn.1000-6362.2016.06.007

陈纪波,胡慧,陈克垚,等.基于非线性PLSR模型的气候变化对粮食产量的影响分析[J].中国农业气象,2016,37(6):674-681