一种通用的多电平逆变器三维空间矢量调制算法研究

王 翠 唐雄民 冯锵健 陈思哲 章 云

(1.广东工业大学自动化学院 广州 510006 2.南昌工程学院江西省精密驱动与控制重点实验室 南昌 330099)



一种通用的多电平逆变器三维空间矢量调制算法研究

王 翠1，2唐雄民1冯锵健1陈思哲1章 云1

(1.广东工业大学自动化学院 广州 510006 2.南昌工程学院江西省精密驱动与控制重点实验室 南昌 330099)

提出了三维空间矢量调制算法，直接将三相参考电压映射到三维空间坐标系，所得基本矢量与开关状态矢量一一对应，不存在冗余现象。该调制算法首先确定参考矢量所在单位正方体的位置，然后在这个单位正方体上寻找合成参考矢量的4个基本矢量，利用伏秒平衡原理计算各基本矢量的作用时间，最后采用七段算法实现在4个基本矢量之间的切换。该算法不需要坐标变换，参考矢量定位简单，与逆变器的电平数无关。三级七电平逆变器仿真和实验结果验证了所提出方法的正确性与可行性。

多电平逆变器 空间矢量调制 零序电压 切换路径

0 引言

空间矢量调制(Space Vector Modulation，SVM)具有直流电压利用率高、输出波形谐波含量低和易于数字化实现等优点[1-3]。基于SVM技术的优点，SVM技术应用于多电平逆变器引起了国内外学者的密切关注[4-7]。到目前为止，大部分多电平逆变器SVM算法是将三相参考电压转换成某一特定二维坐标系中的参考电压矢量轨迹曲线(即3/2转换)，然后根据伏秒平衡原理，利用二维坐标中的基本矢量逼近参考电压矢量。这种调制原理已成为多电平逆变器调制技术的首选方案，并在实际中得到广泛应用。但由于将三相参考电压转换为二维坐标系中的参考电压矢量时存在坐标变换，首先，根据所选择二维坐标系的不同，坐标变换的难易程度不同；其次，在二维坐标系中，很难实现对参考电压矢量的采样，并找到逼近参考电压矢量的基本矢量(即参考矢量定位)；最后，要实现SVM，必须根据基本矢量计算出变换器各相开关的通断状态(即2/3转换)，由二维的基本矢量计算三相的开关通断状态(开关通断状态即开关状态矢量)，这是一个非齐次方程组，因而所得开关状态矢量不是惟一解，这就导致了开关状态矢量的选择很困难。出现这一系列问题的原因是将三相参考电压转换成二维特定坐标系中的参考电压矢量的过程中存在信息的丢失，因此在逆变换的过程中不能复现原来的信息。

基于上述原因，三维空间矢量调制算法被提出。三维空间矢量调制算法的坐标系有两种，文献[8-11]采用的是α-β-0(或表示为α-β-γ)三维直角坐标系，文献[12-15]采用的是A-B-C(或表示为a-b-c)三维直角坐标系。α-β-0坐标系仍沿用二维坐标下的空间矢量调制算法的方法，在原来的二维坐标上增加了零序电压坐标分量，这种坐标系可通过对零序电压分量的研究，将由基本矢量计算开关状态矢量的非齐次方程组变成齐次方程组，但坐标变换并没有简化。A-B-C坐标系早在2000年初就被提出[12]。文献[12]中，参考电压矢量被分解成一个偏移矢量和一个两电平矢量，在包含参考矢量的单位立方体内，分别以偏移矢量及其对角矢量为起点和终点，寻找不同的路径，即可得到逼近参考矢量的4个基本矢量。与传统二维空间矢量调制算法相比，这种算法简单，不需要进行坐标变换、查表和三角函数运算，且不受电平数的限制。文献[13]本质上与文献[12]一致，且文献[13]只考虑了文献[12]中的第2、3种情况。根据文献[12]的原理，在每个采样点都将出现一次零序电压的幅值为+2/3或-2/3电平的情况。当多电平逆变器作为电机的驱动电源时，零序电压就表现为共模电压，高频共模电压会使电机出现轴电压和轴电流[16-18]。轴电流使轴承局部温度迅速升高，产生熔化性凹点，增加轴承机械磨损，同时还会产生噪声，降低轴承的机械寿命。

为了有效抑制零序电压，本文提出一种新的三维空间矢量调制算法，这种算法可大大减少+2/3或-2/3电平出现的频率，有效抑制轴电流过大的情况。

1 三维SVM算法的原理

1.1 n电平逆变器开关状态矢量在三维空间坐标中的分布

A-B-C三维直角坐标系的A、B和C三个坐标轴分别表示三相电压，其方向如图1所示。将开关状态矢量S(a，b，c)(其中a、b、c分别表示三相输出电平的大小)映射到三维空间坐标系中，n电平逆变器有n3个开关状态矢量，这些开关状态矢量构成三维坐标上的基本矢量，分布于棱长为1的正方体(称单位正方体)的顶点。七电平逆变器的开关状态矢量分布如图1所示。

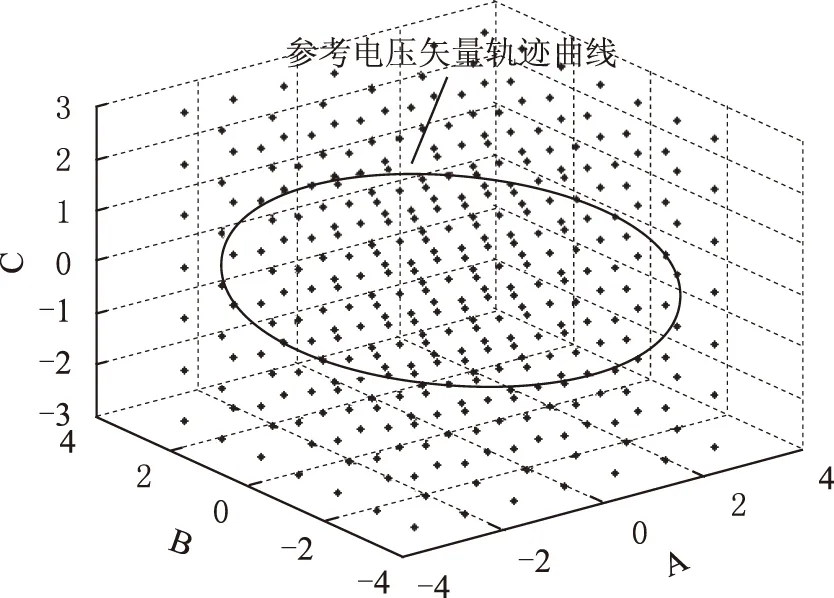
图1 七电平逆变器基本矢量及参考电压矢量轨迹Fig.1 Basic vector and reference voltage vector trajectory of seven-level inverter

1.2 参考电压的归一化及其在三维空间坐标中的参考矢量轨迹曲线

设n电平逆变器的参考电压为ura、urb、urc， 以电压E(E为确保归一化后的三相参考电压在n电平范围内)为基准，取归一化得

(1)

式中，aref、bref、cref分别为相电压的归一化值。将参考矢量Vr(aref，bref，cref)(其中Vr表示参考矢量，(aref，bref，cref)表示该参考矢量的坐标，后面的矢量表示相同的意思)投影到A-B-C三维直角坐标系即可得到参考电压矢量轨迹曲线，如图1所示。

1.3 合成参考矢量的等效基本矢量定位

对参考矢量各分量分别取整得

(2)

式中，floor(*)表示向下取整。

零序电压N为

(3)

由于参考矢量Vr(aref，bref，cref)位于以基本矢量(a，b，c)和(a+1，b+1，c+1)为对角线确定的单位正方体内，因此

(4)

基本矢量(a，b，c)和(a+1，b+1，c+1)的零序电压分别表示为N(a,b,c)和N(a+1,b+1,c+1)。

由三相对称参考电压可得

aref+bref+cref=0

(5)

因此

(6)

(7)

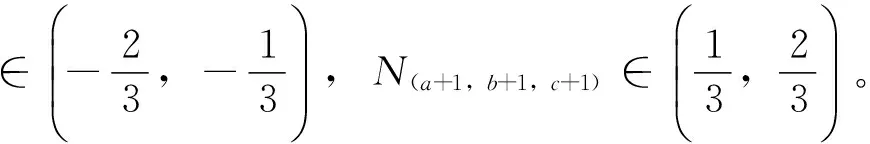
图2 参考矢量定位原理Fig.2 Principle diagram of reference vector locating

1)计算距离参考矢量最近的基本矢量

确定距离参考矢量最近的基本矢量为第一个合成参考矢量的等效基本矢量V1， 判断的方法以及所得等效基本矢量V1的坐标见表1，即将单位正方体用a+0.5、 b+0.5、 c+0.5三个平面分隔成8个小正方体，每个小正方体包含一个基本矢量，参考矢量位于哪一个小正方体，该小正方体包含的基本矢量即为距离参考矢量最近的基本矢量。

2)确定合成参考矢量的另外3个基本矢量

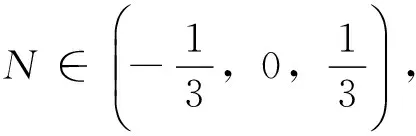
表1 判断逼近参考矢量Vr的基本矢量V1的坐标Tab.1 The coordinates of basic vector V1 approximating reference vector Vr

表2 由V1与Vr确定另外3个逼近Vr的基本矢量V2、V3、V4的坐标Tab.2 The coordinates of basic vectors V2、V3 and V4 synthesizing reference vector V1 and Vr

1.4 参考矢量Vr的合成及其基本矢量作用时间计算

根据伏秒平衡原理，用基本矢量V1、V2、V3、V4合成参考矢量Vr。

(8)

式中，t1、 t2、 t3和t4分别为V1、V2、V3、V4的作用时间;TS为采样周期。表3给出了表2中6种情况下基本矢量V1、V2、V3、V4的作用时间。

采用七段调制算法实现在V1、V2、V3、V4之间的切换，切换路径为V1→V2→V3→V4→V3→V2→V1，以表3中的第1种情况为例，其切换路径如图3所示。

表3 表2中不同情况下基本矢量V1、V2、V3、V4的作用时间Tab.3 The dwelling time of basic vectors V1，V2，V3 and V4 in Tab.2

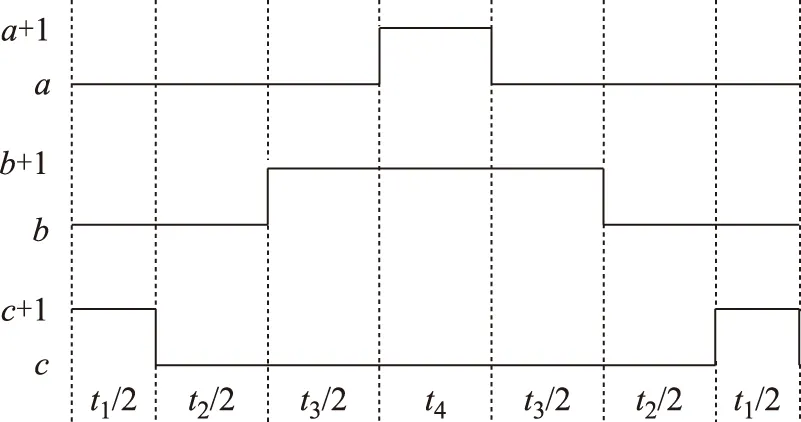
图3 一个周期内切换路径及其作用时间分配Fig.3 Switching paths and dwelling time in a sampling period

2 零序电压分析

文献[12]中，合成参考矢量的基本矢量必须包含基本矢量(a，b，c)和(a+1，b+1，c+1)，以表1中的第1种情况为例，利用式(6)分别计算基本矢量(a，b，c)和(a+1，b+1，c+1)的零序电压N(a,b,c)和N(a+1,b+1,c+1)。 根据表1的判断依据可得

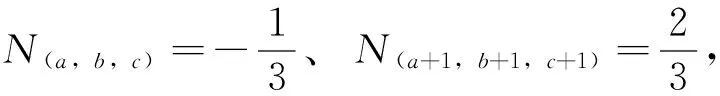
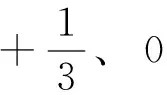
3 实验和仿真结果

本文使用Matlab分别建立了通用的直接的多电平逆变器三维空间矢量调制算法的仿真模型以及文献[12]的仿真模型。仿真的条件：归一化后的参考电压为

(9)

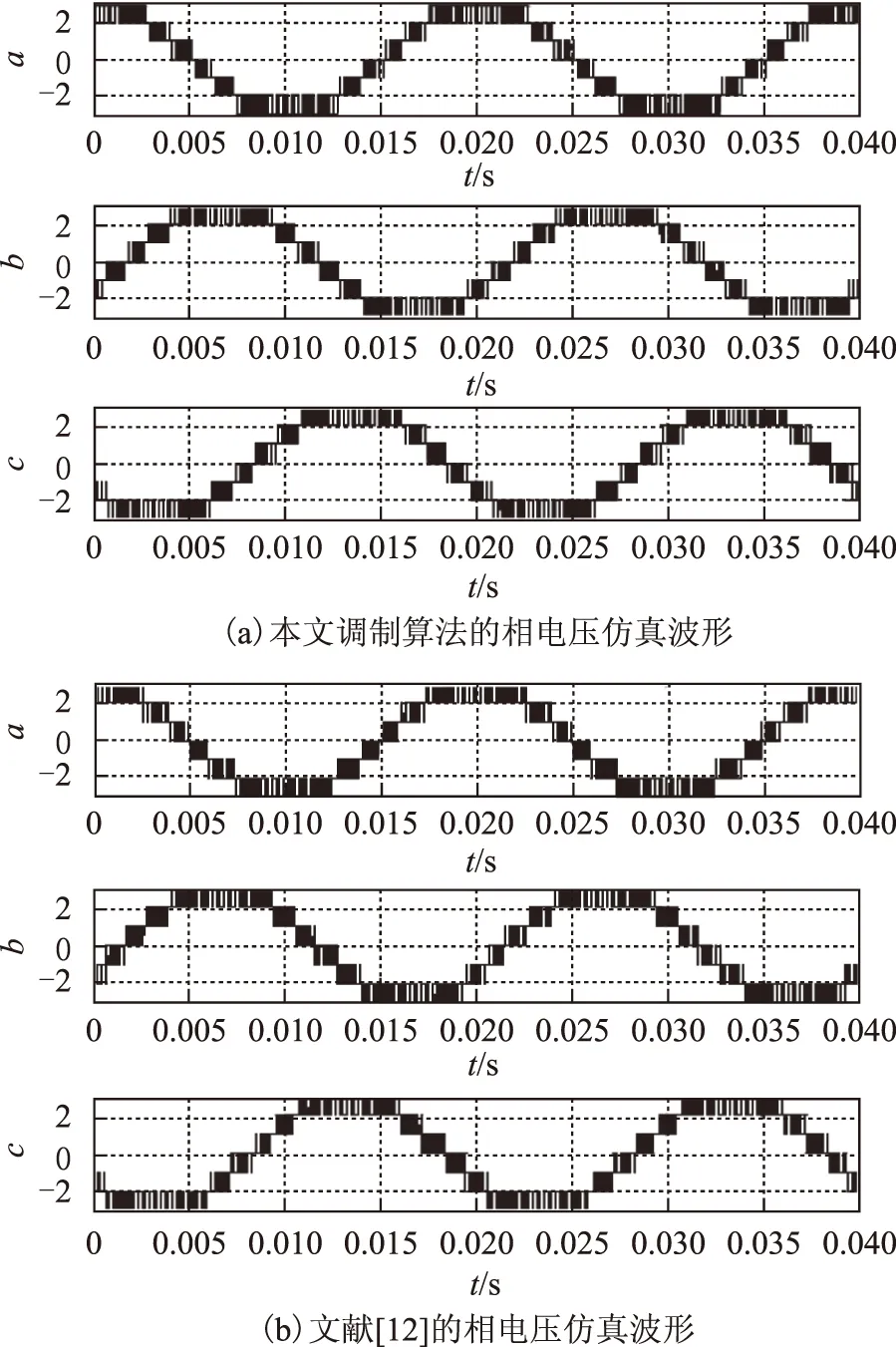
图4 相电压仿真波形Fig.4 Simulation waveforms of phase voltage

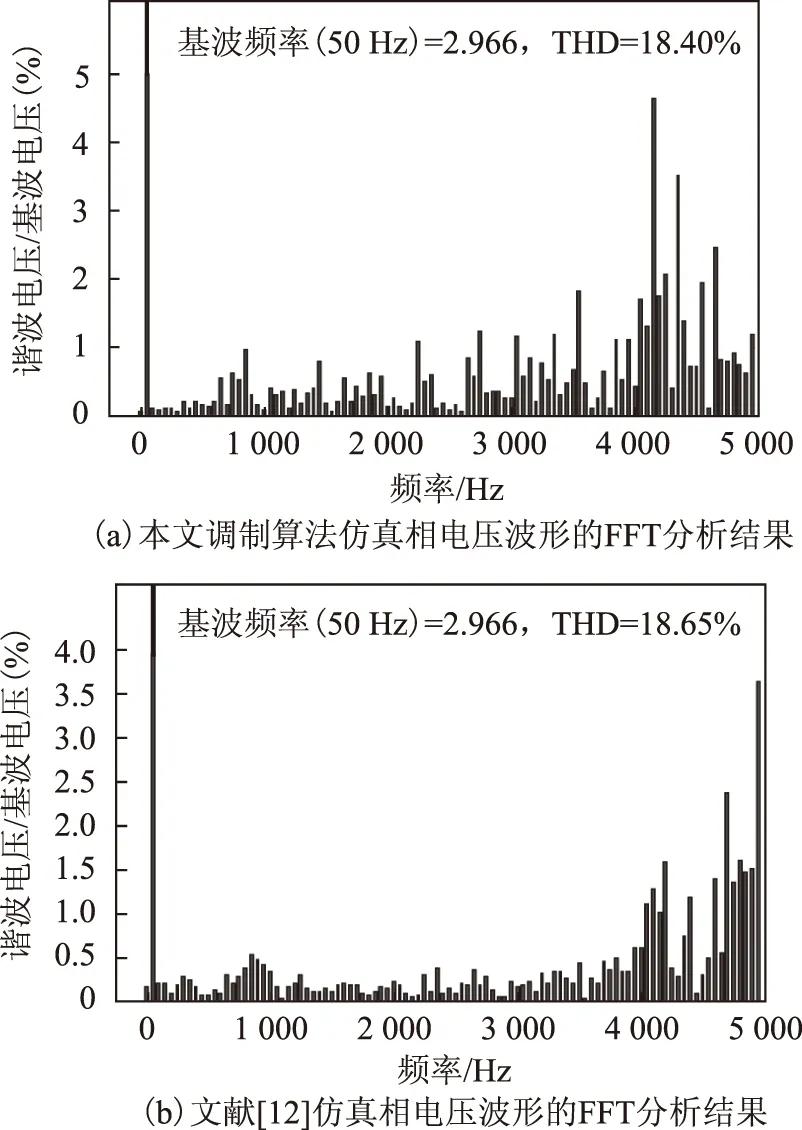
图5 仿真相电压波形的FFT分析结果Fig.5 Harmonic spectrum of phase voltage

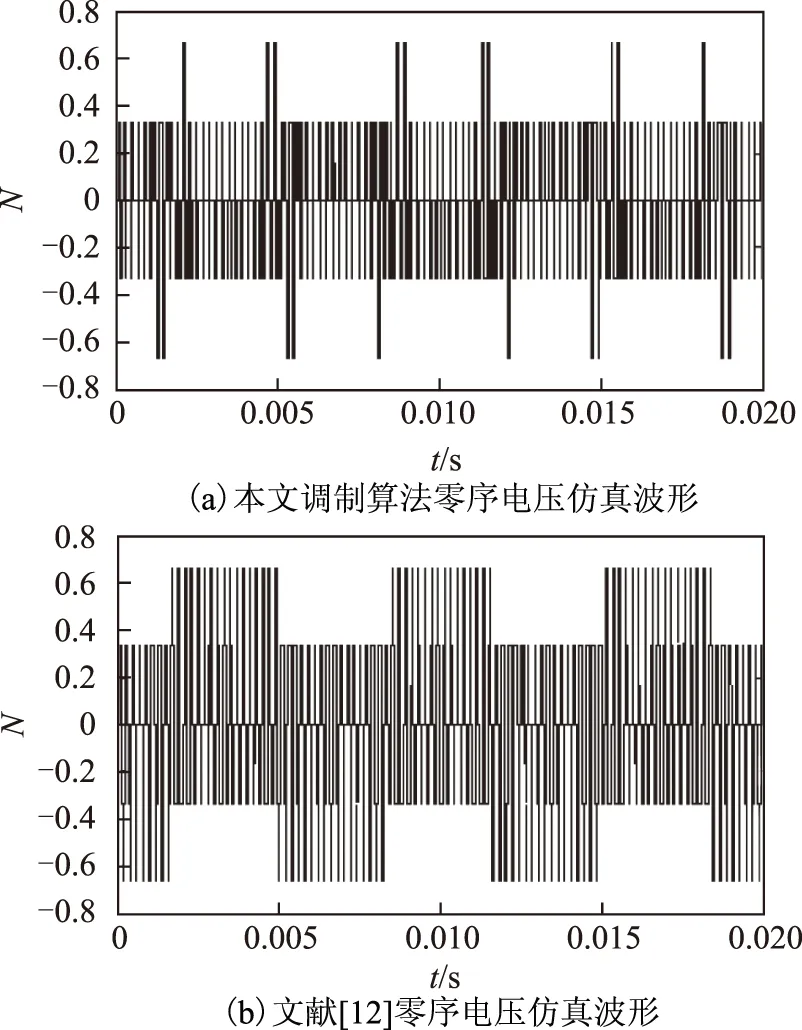
图6 零序电压仿真波形Fig.6 Simulation waveforms of phase voltage

建立七电平逆变器实验平台，实验模型如图7所示。七电平逆变器的每一相包含3个单元，每个单元采用AC-DC-AC的结构，即采用单相桥式整流提供直流电压，利用所得稳定的直流电压作为逆变桥的输入电源，逆变桥的开关管使用MOSFET管IRF460。本实验的控制器采用TMS320F28335，驱动电路采用IR2110，负载采用A02-7114型三相异步电动机，电动机Y形联结，实验采用泰克TPS2024B型示波器测试波形。单相桥式整流模块的输入电源电压为AC 60V，给定参考信号如式(9)所示。图8为相电压和线电压实验波形，图9为相电压和零序电压实验波形。

图7 七电平实验平台照片Fig.7 Photograph of the seven-level prototype

图8 相电压和线电压实验波形Fig.8 Experimental waveforms of phase voltage and line voltage

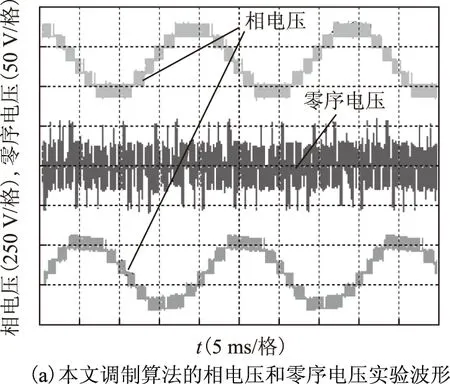
图9 相电压和零序电压实验波形Fig.9 Experimental waveforms of phase voltage and zero order voltage

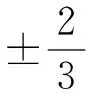
4 结论

本文在A-B-C坐标系上研究多电平逆变器三维空间矢量调制算法，该算法避免了坐标变换，且开关状态矢量与基本矢量一一对应，参考矢量的定位简单。从仿真和实验结果可以看出，在一个基波周期内，本算法所得零序电压为±2/3电平的比率非常低，而参考文献[12]在每一次采样周期至少会出现一次零序电压为2/3或-2/3电平，即本算法有效抑制了逆变器输出的共模电压。

[1] 姜卫东，王群京，史晓峰，等.基于矩阵变换的N电平逆变器通用SVPWM算法[J].电工技术学报，2009，24(5)：86-91. Jiang Weidong，Wang Qunjing，Shi Xiaofeng，et al.General SVPWM algorithm for N level inverter based on matrix transformation[J].Transactions of China Electrotechnical Society，2009，24(5)：86-91.

[2] 李继华，阮新波，王学华.级联型多电平逆变器线电压谐波优化的SVPWM策略[J].电工技术学报，2014，29(6)：120-128. Li Jihua，Ruan Xinbo，Wang Xuehua.A SVPWM strategy with optimal line-to-line voltage harmonic spectrum for cascaded multilevel inverters[J].Transactions of China Electrotechnical Society，2014，29(6)：120-128.

[3] Kouro S，Malinowski M，Gopakumar K，et al.Recent advances and industrial applications of multilevel converters[J].IEEE Transactions on Industrial Electronics，2010，57(8)：2553-2580.

[4] 王翠，孟志强.N级逆变器空间矢量调制的开关频率优化算法[J].中国电机工程学报，2011，31(36)：46-52. Wang Cui，Meng Zhiqiang.An optimal algorithm on switching frequency of space vector modulation for N-cell inverter[J].Proceedings of the CSEE，2011，31(36)：46-52.

[5] Effah F B，Wheeler P，Clare J，et al.Space-vector-modulated three-level inverters with a single Z-Source Network[J].IEEE Transactions on Power Electronics，2013，28(6)：2806-2815.

[6] Deng Y，Teo K H，Duan C，et al.A fast and generalized space vector modulation scheme for multilevel inverters[J].IEEE Transactions on Power Electronics，2014，29(10)：5204-5217.

[7] 刘云峰，何英杰，尹仕奇，等.基于空间矢量调制的星形级联H桥SVG直流侧电压控制方法研究[J].电工技术学报，2015，30(5)：23-32. Liu Yunfeng，He Yingjie，Yin Shiqi，et al.Research on DC voltage control based on space vector modulation method in the star connection cascaded H-bridge SVG[J].Transactions of China Electrotechnical Society，2015，30(5)：23-32.

[8] Wong M，Tang J，Han Y.Cylindrical coordinate control of three-dimensional PWM technique in three-phase four-wired trilevel inverter[J].IEEE Transactions on Power Electronics，2003，18(1)：208-220.

[9] Zhang R，Prasad V H，Boroyevich D，et al.Three-dimensional space vector modulation for four-leg voltage-source converters[J].IEEE Transactions on Power Electronics，2002，17(3)：314-326.

[10]莫志禄.四桥臂有源电力滤波器三维空间矢量调制技术的研究[J].现代电子技术，2011，34(24)：37-40. Mo Zhilu.Research of three-dimensional space vector modulation for active power filter with four-leg[J].Modern Electronics Technique，2011，34(24)：37-40.

[11]陈新，龚春英，郦鸣，等.应用于三相变换器的三维空间矢量调制[J].南京航空航天大学学报，2002，34(2)：148-153. Chen Xin，Gong Chunying，Li Ming，et al.3-D space vector modulation in three-phase inverter[J].Journal of Nanjing University of Aeronautics & Astronautics，2002，34(2)：148-153.

[12]Prats M M，Franquelo L G，Portillo R，et al.A 3-D space vector modulation generalized algorithm for multilevel converters[J].IEEE Power Electronics Letters，2003，1(4)：110-114.

[13]Dai N，Wong M，Chen Y，et al.A 3-D generalized direct pwm algorithm for multilevel converters[J].IEEE Power Electronics Letters，2005，3(3)：85-88.

[14]高宁，罗悦华，王勇，等.基于 FPGA 的三电平风电变流器三维空间矢量调制算法[J].电工技术学报，2013，28(5)：227-232. Gao Ning，Luo Yuehua，Wang Yong，et al.3D space vector modulation algorithm based on FPGA for three-level wind power converter[J].Transactions of China Electrotechnical Society，2013，28(5)：227-232.

[15]Perales M A，Prats M M，Portillo R，et al.Three dimensional space vector modulation in abc coordinates for four-leg voltage source converters[J].IEEE Power Electronics Letters，2003，1(4)：104-109.

[16]钟玉林，赵争鸣，袁立强.逆变器驱动电机的共模电压和轴电压的抑制[J].清华大学学报(自然科学版)，2009，49(1)：25-28. Zhong Yulin，Zhao Zhengming，Yuan Liqiang.Suppression of common-mode and shaft voltages in inverter-driven induction motor[J].Journal of Tsinghua University (Science and Technology)，2009，49(1)：25-28.

[17]佘阳阳，杨柏旺，吴志清，等.基于载波和空间矢量调制之间联系的多电平VSI降低和消除共模电压的PWM策略[J].电工技术学报，2015，30(4)：171-178. She Yangyang，Yang Bowang，Wu Zhiqing，et al.PWM algorithm for multi-level VSI with reduced and eliminated common mode voltage based on relationship between CBPWM and SVPWM[J].Transactions of China Electrotechnical Society，2015，30(4)：171-178.

[18]白保东，刘威峰，王禹，等.PWM 驱动感应电机轴电压轴承电流[J].电工技术学报，2013，28(S2)：434-440. Bai Baodong，Liu Weifeng，Wang Yu，et al.Research on shaft voltage and bearing current of induction motor driven by pwm inverter[J].Transactions of China Electrotechnical Society，2013，28(S2)：434-440.

A Generalized Three-Dimensional Space-Vector Modulation Algorithm for Multilevel Converters

Wang Cui1，2Tang Xiongmin1Feng Qiangjian1Chen Sizhe1Zhang Yun1

(1.Guangdong University of Technology Faculty of Automation Guangzhou 510006 China 2.Jiangxi Province Key Laboratory of Precision Drive and Control Nanchang Institute of Technology Nanchang 330099 China)

The proposed three-dimensional (3D) space-vector modulation (SVM) algorithm maps switching state vectors in 3D space coordinates directly.Every basic vector only matches a switching state vector.And without redundancy phenomenon.Firstly，the location of a unit cube which includes the reference voltage vector is fixed.Secondly，in the unit cube，four basic vectors which synthesize the reference vector are confirmed.The dwelling times of the basic vectors are calculated according to volt-second balance principle.Finally,switching among the four basic vectors is implemented by seven-segment modulation algorithm.Coordinate transformation is not required in this proposed algorithm.Reference vector location is fixed simply.The proposed algorithm is also independent of the level number of the inverter.The correctness and feasibility of this proposed algorithm are verified by the simulation and experimental results of a three-cell seven-level inverter.

Multilevel inverter，space vector modulation (SVM)，zero order voltage，switching path

国家自然科学基金(51207026，51307025)和江西省自然科学基金(20151BAB206049)资助项目。

2015-05-12 改稿日期2015-07-31

TM464

王 翠 女，1973年生，副教授，博士，研究方向为电力电子电源技术。

E-mail：ouyang_wangcui@163.com(通信作者)

唐雄民 男，1977年生，副教授，博士，研究方向为电力电子变流技术。

E-mail：tangxiongmin@126.com