基于静态非合作博弈的电动汽车充电电价影响因素量化分析
2016-12-27孙丙香阮海军许文中姜久春龚敏明
孙丙香 阮海军 许文中 姜久春 龚敏明
(1.国家能源主动配电网技术研发中心(北京交通大学) 北京 100044 2.北京交通大学北京电动车辆协同创新中心 北京 100044)
基于静态非合作博弈的电动汽车充电电价影响因素量化分析
孙丙香1,2阮海军1,2许文中1,2姜久春1,2龚敏明1,2
(1.国家能源主动配电网技术研发中心(北京交通大学) 北京 100044 2.北京交通大学北京电动车辆协同创新中心 北京 100044)
电动汽车的大规模推广应用需要合理地制定充电电价,运用博弈论分析了电动汽车发展相关的主要三方——政府、充电设施运营商和用户的利益关系,构建了关于充电电价和电动汽车发展规模的三方博弈模型,并针对静态非合作博弈方式进行了博弈求解。以珠三角9个城市电动汽车数据为例,得到了分别以充电设施运营商和政府为博弈主导方的博弈均衡解,在此基础上定量分析了5个影响因素变动幅度改变的条件下,充电电价和电动汽车保有量的变化趋势,以及各影响因素对充电电价和电动汽车保有量的敏感程度。最后在政府给予充电设施运营商适当补贴的情况下得到双方可接受的博弈均衡解,并对用户的广义成本进行分析,合理的充电定价能够满足三方的利益诉求,有利于电动汽车的大规模推广。
电动汽车保有量 充电电价 静态非合作博弈
0 引言
能源紧缺和环境污染的双重压力助推了电动汽车的快速发展,新能源汽车以节能环保的优势,被列为我国七大战略新兴产业之一。2012年6月,国务院提出我国纯电动汽车和插电式混合动力汽车累计产销量力争到2015年达到50万辆,到2020年达到500万辆[1]。
随着电动汽车的大规模推广,如何有效地制定合理的充电电价成为急需解决的关键问题[2]。充电电价的制定是一个复杂的系统工程,仅仅为了削峰填谷而采用峰谷电价[3]并没有考虑充电电价对电动汽车发展的影响,只考虑了对电网的影响却忽视了政府推广电动汽车的目标,充电定价有多个因素相互联系、相互制约[4],因此要制定合理的充电电价,需要对多方利益主体综合考虑。文献[5,6]考虑各个用户的利益,将博弈论应用于电动汽车接入电网后的能量管理,文献[7]运用博弈论研究了多个零售商竞争同一市场的价格竞争策略,并求解了价格均衡点。文献[8]考虑电网公司和电动汽车用户的非合作博弈关系来优化充电电价,但是并未考虑商业化运行前政府在充电电价制定中的引导作用。文献[9]利用静态非合作博弈方法,实现插电式混合电动汽车的充电负荷分配的稳定性和鲁棒性,但是并未涉及充电定价问题。文献[10]运用博弈论对充电电价进行了量化分析,但仅仅考虑了政府支持力度对充电电价的影响,并没有考虑其他更重要因素,如电池价格、电池寿命等。文献[11]通过对各方的收益函数进行博弈求解,得到相应的充电定价和政府支持力度,但其模型的建立是基于假设各因素恒定,难以考虑市场波动(如电池价格下降等)情形下,充电电价和电动汽车发展规模的测算,更无法评估各影响因素对充电电价的敏感程度。
本文通过引入Logit模型建立了涉及政府、充电设施营运商和用户利益的三方博弈模型。运用静态非合作博弈求解方法量化分析5个影响因素,即可能的市场波动情形,分别对充电电价和电动汽车保有量的敏感程度,分析符合博弈三方利益的充电定价策略,为电动汽车充电电价的合理制定提供理论依据。
1 原理
1.1 Logit模型
Logit模型也称“分类评定模型”,是最早的也是应用最广的离散选择模型[12]。Logit模型与最大效用理论是一致的,该模型具有求解速度快、应用方便和概率表达式显性等特点。本文在个体选择电动汽车或传统汽车的意向中,引入Logit模型来量化计算个体购买电动汽车的概率。Logit模型[13]中,定义“选择枝”为可供人们选择的选项,每个选择枝根据特征的不同具有不同的“效用”,为了定量分析各个特征变量对个体购买电动汽车意向的影响,电动汽车的效用函数可表示为多项式
Si,q=βi,qXi,q+εi,q
(1)
式中,i为选择枝;q为个体;βi,q为反映个体偏好的待估参数矢量;Xi,q为反映选择枝属性特征的变量;εi,q为选择枝i的属性特征和个体特征及影响个体选择的因素中的随机的不可观测效用部分。若假定εi,q相互独立且服从相同的概率分布,则个体q选择选择枝i的概率[14]为
(2)
式中,k为不同的选择枝;Xi,q根据选择枝的特征进行设定,本文通过对消费者购买汽车时的心理行为的分析,设定了车辆综合成本、环境需求度、续驶里程、综合故障率、政府支持度、售后服务水平6个特性矢量[15]来反应电动汽车或传统汽车的效用值大小,其中车辆综合成本包括购置成本、运行成本等因素。
单位充电电价直接决定了消费者使用电动汽车的运行成本大小,而运行成本则是消费者选择电动汽车或传统汽车的重要影响因素之一。消费者对电动汽车的偏好程度将会直接影响电动汽车的推广进度[16],影响电动汽车在整个私人汽车市场的分担率[14]。电动汽车的市场分担率v为
(3)
式中,β1、X1分别为反映个体对车辆综合成本偏好的待估参数矢量和车辆综合成本的属性特征矢量;βk、Xk分别为反映个体对环境需求度、续驶里程、综合故障率、政府支持度、售后服务水平偏好的待估参数矢量和相应选择枝的属性特征矢量;a为车辆运行成本与车辆综合成本的比值;βck、Xck分别为反映个体对传统汽车各选择枝的待估参数矢量和各选择枝的属性特征矢量。
1.2 静态非合作博弈
博弈论是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题的理论。由于博弈各方的相互依存性,博弈结构依赖于每一个局中人的决策[17],一方面是指局中人如厂商进行生产是为了追求最大的利润,另一方面它使得局中人之间产生竞争。博弈的一个标准表达式为
G={S1,S2,…,Si,…,Sn;u1,u2,…,ui,…,un}
(4)
式中,Si为局中人i的策略空间,Si=(si1,si2,…,sik),i=1,…,n,n为局中人个数,Si共有ki个策略;ui为局中人i的收益函数。
静态博弈是指参与者同时采取行动,或者尽管参与者行动的采取有先后顺序,但后行动的人不知道先采取行动的人采取的是什么行动[17],如田忌赛马博弈。非合作博弈是指参与者在行动选择时无法达成约束性的协议[18]。Stackelberg博弈模型是最常见的非合作博弈模型,Stackelberg问题可以表示成数学二层(多层)规划问题[19]。
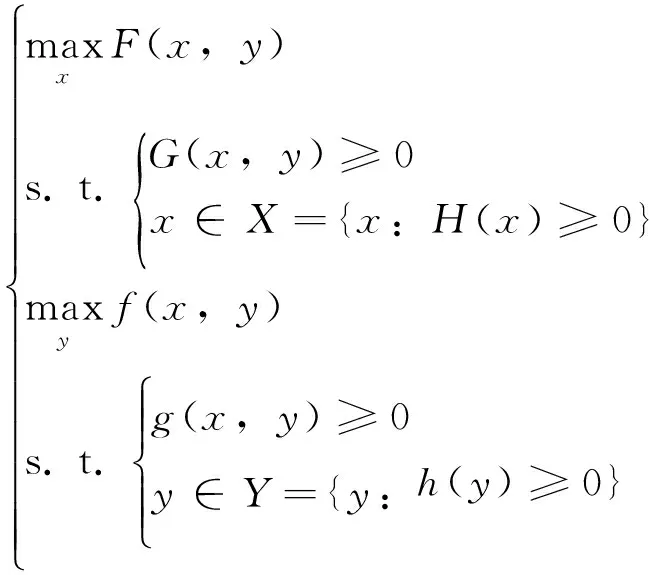
(5)
式中,F(x,y)、G(x,y)和H(x)分别为上层规划的目标函数、约束条件和变量的定义域;f(x,y)、g(x,y)和h(y)分别为下层规划的目标函数、约束条件和变量的定义域,x、y为变量。
在Stackelberg博弈中,存在两种类型的决策者:处于较高决策层次的“主导者”和处于下级决策层次的“跟随者”。“主导者”根据拥有的信息预测“跟随者”的反应[20],然后选择策略空间中的一个最优战略。同样的,“跟随者”根据拥有的信息预测“主导者”的反应来选择自身收益最大的策略,最后两者达到非合作的最优战略,即达到静态博弈均衡。
2 政府、充电设施运营商和用户三方博弈模型
从政府角度看,电动汽车产业化能够减少环境污染,降低对石油的依赖,促进产业升级等,电动汽车发展所带来的综合效益使得政府对电动汽车产业进行大力支持;充电设施运营商是以盈利为目的的企业,建设与运营充电设施的成本越高,为了赚取更高的利润,充电电价必然会越高;消费者个人环保意识的高低,消费者对充电电价、政策变动的敏感程度和对电动汽车关键技术变动的敏感程度等都影响着消费者的购买行为。如图1所示,本文对电动汽车发展密切相关的主体——政府、充电设施运营商和用户,构建涉及三方利益的博弈模型。
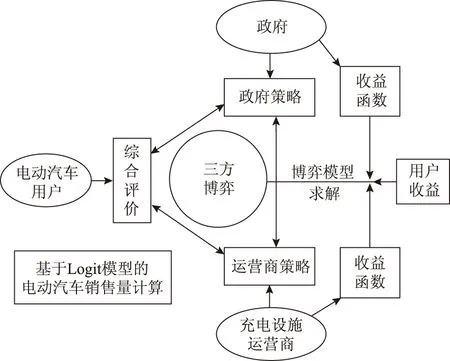
图1 关于充电定价和车辆保有量预测的博弈模型Fig.1 The tripartite game model about the charge electricity price and EV holdings
根据私人汽车市场的历史数据预测未来私人汽车的整体销售量,利用Logit模型,推导关于充电电价的电动汽车的市场分担率函数,从而求得电动汽车每年的新增量,新增量逐年累计相加即为电动汽车市场保有量。从政府、充电设施运营商和用户三者的策略和利益角度出发,建立了三方关于充电电价及政府支持度的博弈函数模型,然后利用静态非合作博弈方法对三方收益进行求解,得到不同情况下博弈均衡解,然后在此基础上进行充电电价的影响因素量化分析。
2.1 博弈三方的策略集合
政府、充电设施运营商和用户是3个博弈方。政府的策略集合为政策支持和政府补贴大小,本文只考虑对单个标准充电设施建设的补贴率SE(0
2.2 博弈三方的收益函数
1)政府收益函数。
在推广电动汽车过程中,政府获益是每辆电动汽车带来的综合效益,其成本是给充电设施运营商和用户的补贴[11],则其每年的收益函数ПG为
(6)
式中,B为单位电动汽车每年为政府带来的综合收益;CD为单位标准充电设施的建设成本;m为当年区域内充电设施的建设量;N为充电设施的使用年限;q为当年电动汽车的新增量,是关于单位销售电价P的函数;Q可由q逐年累加而得;N1为电动汽车的使用年限;SCq/N1粗略地表示平均每年政府对购买电动汽车需支付的补贴成本。由于B的估值涉及到很多因素,而且存在很多不确定的因素,很难进行量化,因此本文将政府的收益设定为电动汽车的保有量,电动汽车保有量多就意味着政府的收益高,这也是符合式(6)的。
2)充电设施运营商收益函数。
在推广电动汽车过程中,充电设施运营商获益是充电差价收益和政府补贴,其成本是建设和运营维护充电设施,则其每年的收益函数ПE为
(7)
式中,Cp为单位电能的成本价格;Q为当年电动汽车累计保有量;F为平均单位电动汽车的年需求电量;Cγ为单位标准充电设施的年运营成本,假设私人电动汽车的年运行成本为充电桩建设成本的10%;M为当年区域内的电动汽车充电设施总量,是每年区域内充电设施建设量m的累计量。
3)电动汽车用户收益函数。
仅从电动汽车和传统汽车的经济上分析,购买和使用传统汽车与电动汽车的成本之差为用户的收益函数ПC为
ΠC=Coi-(1-SC)Cgi-Cri-Chi
(8)
式中,Cgi为第i年电动汽车的购置成本;Chi为第i年电动汽车的电池更换成本;Cri为第i年电动汽车的运行成本,其值为电动汽车行驶里程与充电电价的乘积;Coi为第i年传统汽车的购置成本与运行维护成本之和。
2.3 基于Logit模型的多影响因素的量化
用户根据电动汽车特性矢量来综合评价电动汽车,进而决定是否购买电动汽车,各特性矢量的属性值由调查用户对电动汽车体验得到,数据来自文献[15],见表1。环境需求度、续驶里程、综合故障率、售后服务水平的打分值由专家打分决定,各打分值来自参考文献[15],见表2。打分值即为反映个体对电动汽车偏好的各个选择枝的待估参数矢量,假设传统汽车的各打分值均为1,而对政府给用户的补贴和车辆综合成本的打分值进行量化分析,以客观定量地描述市场波动对充电电价和车辆保有量的影响。

表1 电动汽车各特性矢量属性值Tab.1 The property values of feature vector in EVs

表2 关键年份电动汽车的特征矢量预测Tab.2 The feature vector prediction of EV sat key years
1)政府补贴。
政府给用户的补贴,表征对电动汽车用户的政策支持力度,其初始年份(2015年)打分值d1由专家打分决定,而后的打分为dn=1+(d1-1)Bn/B1,以量化政府补贴力度,Bn为第n年用户购买一辆电动汽车政府给的补贴金额数,B1为第1年用户购买一辆电动汽车政府给的补贴金额数,补贴金额数均来自新的政策文件[21]。这样随着政府给用户的补贴金额数的下降,打分值随之下降,私人汽车的初始年份专家打分为1.5[15]。
2)电池价格与电池寿命。
电动汽车的广义成本包括电池购置成本、裸车成本、电池更换费用和运行维修成本[22]。初始年份电池包的购置成本为Ba0万元,初始年份的电池单价为Ce0元/(W·h),假设电池单价每年下降幅度相等为Δcell元/(W·h),电池组寿命为Li,假设电池寿命平均每年增加Δlife,电动汽车的裸车成本为Lc万元。
(9)
式中,Cci为第i年电动汽车的购置成本与电池更换成本之和;k1、k2分别为电动汽车购置和电池更换时企业的盈利系数,本文取0.75;nj为初始电池包的使用年限;Lix为电动汽车相当于传统汽车行驶30万km的循环寿命。
3)汽油价格。
传统汽车的广义成本包括车辆购置成本和运行维修成本,其中初始年份汽油价格为Cp0元/升,假设汽油价格平均每年下降比例相等[23]为Δoil,传统机动车的裸车成本为Lc1万元,传统机动车的百公里耗油为po升,传统机动车的全寿命行驶里程为Ro万km。
Coi=RopoCpi-1(1+Δoil)+Lc1
(10)
式中,Coi为第i年传统汽车的购置成本与运行维护成本之和。
为了分析量化电池价格、电池寿命和汽油价格对充电电价和电动汽车保有量的影响,设定电动汽车的车辆综合成本打分值为传统汽车的广义成本与电动汽车的广义成本之比[24]。
4)充电设施建设成本。
充电设施建设成本包括充电设施初始建设成本及其时间价值,其中投资收益率为dn,初始年份充电设施建设成本中,慢充桩为Cs10元,快速充电桩为Cs20元,假设充电设施建设成本平均每年下降比例相等为Δpile。
(11)
(12)
式中,Bsj为第j年投资收益率之和;Cs1(j-1)为慢速充电桩第j-1年的建设成本,Cs2(j-1)为快速充电桩第j-1年的建设成本;Csokj为k类充电桩第j年的价值;k=1,2。
3 基于静态非合作博弈的充电定价影响因素定量分析
以珠三角9个城市为例,对电池价格、电池寿命、汽油价格、充电设施建设成本和政府补贴5个影响因素进行博弈分析和定量计算,进而在各影响因素变动幅度改变(5个影响的初始变动幅度是根据历史数据预测的,变动幅度的改变是在初始变动幅度的基础上改变得到的)的情况下,量化计算对充电电价和电动汽车保有量的影响,以研究敏感程度较大的影响因素。
根据统计年鉴公布的私人汽车历史数据,预测未来私人汽车车辆数,私人汽车增长率呈现指数规律,将数据以式(13)拟合,误差较小且较为简单。
Qot=Qo(t-1)(1+αe-βt)
(13)
式中,Qot、Qo(t-1)分别为当年和上一年私人汽车的保有量。表3为本文计算的基础数据,数据来源于某市电动汽车的运行数据。电池单价每年下降相等的幅度Δcell设定为0.2元/(W·h),所有数据均根据历史数据拟合得到的。
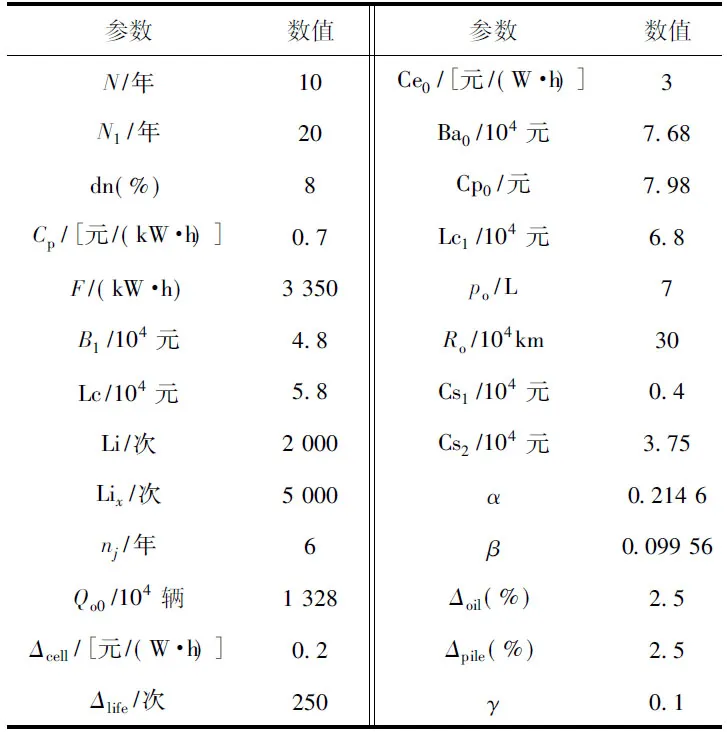
表3 博弈求解的基本数据Tab.3 The basic data for game solving
3.1 静态非合作博弈模型求解
基于logit模型构建了关于充电电价与汽车数量函数关系,将用户策略融合在政府和运营商双方博弈模型中,因此采用静态非合作模型分析政府和充电设施运营商的利益关系。在进行策略选择前,博弈双方参与人都有各自的期望目标,假设充电设施运营商的期望目标为在考虑投资收益率的情况下盈利大于等于0,政府的期望目标为私人汽车辆达到40万辆。
由于模型的非线性特征,在Matlab中求解博弈模型均衡解时,采用搜索迭代方法,基于Stackelberg求解方法的流程图如图2所示。主导博弈的一方目标函数处于下层规划,具有先动优势。SEmax为设置的政府给充电设施营运商的最大补贴,П(i)为跟随者的目标函数。由于博弈各方不在同一行业,各方的利益分配也是不同的,因此设定不同的博弈方,对充电定价和电动汽车的发展进行量化分析。在Matlab中对各方收益进行计算,当充电价格变化时,在考虑投资收益率的情况下,到2020年充电设施运营商的累计收益和私人乘用车保有量的变化趋势如图3所示。充电设施运营商的累计收益随着充电电价的升高逐渐上升,电价越高运营商的收益就越高;私人乘用车保有量随着充电电价的升高逐渐下降,电价越高电动汽车的使用成本越高,消费者购买电动车的概率就越低。

图2 博弈模型求解框图Fig.2 The block diagram for solution of game model

图3 累计收益和车辆保有量随充电电价的变化关系Fig.3 The curves of accumulated earnings and EV holdings along with change of charging electricity price
充电设施运营商作为博弈主导方时,不考虑政府补贴,即SEmax=0,充电定价为1.045 7元时实现6年收益盈亏平衡,此时私人乘用车保有量为34.23万辆。政府作为博弈主导方时,为使私人乘用车保有量达到40万辆,应当定价为0.888 6元,充电设施运营商6年累计亏损4.9亿元。很明显,在非合作博弈中,最终的均衡点向有利于主导博弈方的方向倾斜,而博弈另一方的博弈目标很明显没有实现,即博弈的另一方利益是受损的。
影响因素变动幅度调整时,博弈均衡点将发生变化,充电电价也将随之变动,从而可在各影响因素变动的情况下比较各影响因素对充电电价和电动汽车保有量的敏感程度。为了更好地分析5个影响对充电电价的敏感度,设定SEmax=0,即政府给充电设施营运商的补贴为0。从博弈方的不同利益角度出发,分别以充电设施运营商和政府作为博弈主导方进行影响因素敏感性分析。
3.2 充电设施运营商主导的博弈
当充电定价在合理区间时,充电定价由市场决定,此时可认为充电定价的博弈由充电设施营运商主导,其求解模型为
(14)
式中,ki(i=1,2)分别为快速充电桩和慢速充电桩的配比,慢速充电桩按汽车数量100%配给,快速充电桩按汽车数量5%配给;Qe为政府设定的电动汽车发展目标,即Qe=40万辆;T为计算的总年限,本文设定的为6年。以电池价格下降幅度调整为例,计算初始年份的电池价格为3元/(W·h),根据电池价格的历史数据预测电池价格平均每年下降0.2元/(W·h)。假设电池价格平均每年的下降幅度降低2%,即电池价格每年下降0.14元/(W·h)时,得到均衡结果见表4。充电设施运营商达到盈亏平衡时充电电价定价为1.054 4元/(kW·h),充电电价上涨0.14%;到2020年私人乘用汽车保有量为29.26万辆,汽车数量减少14.50%。
假设电池价格平均每年的下降幅度提高2%,即电池价格平均每年下降0.26元/(W·h)时,充电设施运营商达到盈亏平衡时,充电电价定价为1.044 1元/(kW·h),充电电价下降0.15%;到2020年私人乘用汽车保有量为41.29万辆,汽车数量增加20.64%。电池价格下降幅度调整对充电价格影响较小,而对电动汽车保有量影响较大。
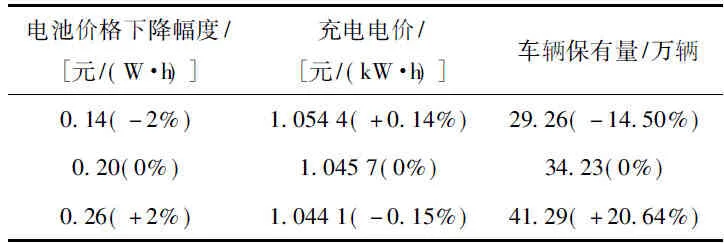
表4 电池价格下降幅度调整后的均衡结果Tab.4 The balanced result when the drop rate of battery price adjusted
和电池价格一样,假设政府补贴下降幅度、循环寿命上升幅度、汽油价格上升幅度和充电设施成本下降幅度都变动±2%时,充电价格变化曲线如图4所示。充电设施运营商主导博弈时,充电设施建设成本下降幅度变动对充电定价影响较大,而且充电价格基本呈线性关系,这是因为充电设施建设成本直接影响着充电设施运营商的收益。
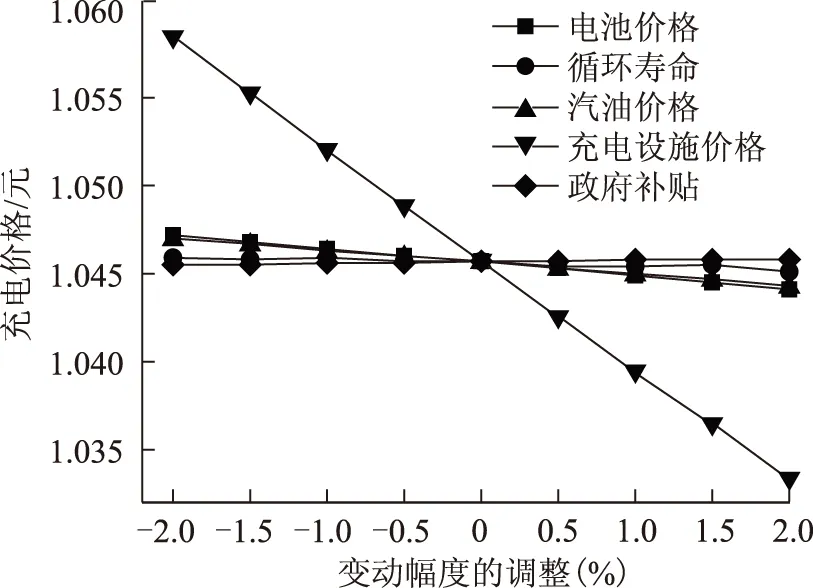
图4 充电电价随各影响因素变动幅度变化±2%关系Fig.4 The curves of charge electricity price changingalong with the ±2% change of amount of variation of various influencing factors
车辆保有量随各影响因素变动幅度变化±2%的关系如图5所示。虽然充电设施建设成本对充电电价的影响较大,但是对车辆保有量影响较小,而电池价格和汽油价格对车辆保有量影响较大,这主要是因为电池成本在电动汽车总成本中所占的比重较大,尤其是更新电池包成本较高。
3.3 政府主导的博弈
当充电定价较高时,用户购买电动汽车的意愿降低,电动汽车的数量难以达到政府的预期目标,政府将会干预充电定价,此时可认为充电定价的博弈由政府主导,其求解模型为
(15)
假设电池价格每年下降0.14元/(W·h)时,得到均衡结果见表5。政府为实现电动汽车达到40万辆的目标,充电电价定价为0.705 6元/(kW·h),充电电价下降20.58%。到2020年充电设施运营商累计亏损10.60亿元,收益减少116.32%。
假设电池价格平均每年的下降幅度为0.26元/(W·h)时,电动汽车达到40万辆时充电电价定价为1.0732元/(kW·h),充电电价增加20.80%。到2020年充电设施运营商累计收益为0.92亿元,收益增加118.68%,电池价格下降幅度调整对充电电价和运营商收益影响较大。
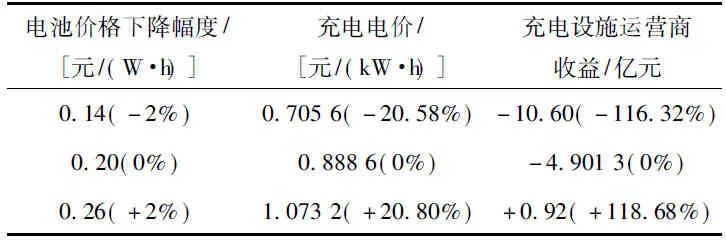
表5 电池价格下降幅度调整后的均衡结果Tab.5 The balanced result when thedrop rate of battery price adjusted
各影响因素变动幅度都调整±2%时的充电价格变化曲线如图6所示,政府主导博弈时,电池价格和汽油价格变动幅度变化对充电定价影响较大。根据Logit模型可知电池价格直接影响车辆保有量,为了保证汽车数量达到目标,充电电价就会出现大幅变化。
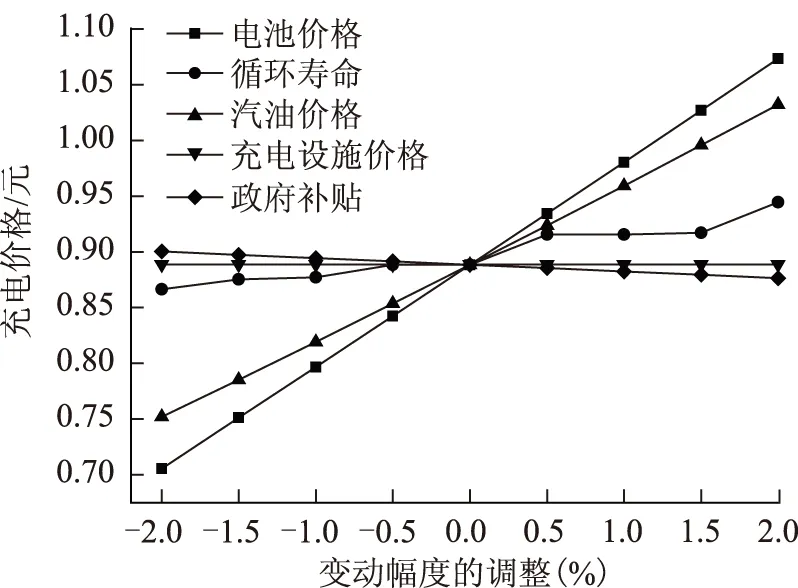
图6 充电电价随各影响因素变动幅度变化±2%关系Fig.6 The curves of charge electricity price changingalong with the ±2% change of amount of variation of various influencing factors
充电设施运营商收益随各影响因素变动幅度变化±2%的关系如图7所示。电池价格和汽油价格对充电设施运营商收益影响较大,这主要是因为充电电价大幅调整后,充电设施运营商的收益也随之大幅波动。

图7 收益随各影响因素变动幅度变化±2%的关系Fig.7 The curves of operators accumulated earnings along with the ±2% change of amount of variation of various influencing factors
3.4 双方可接受的博弈均衡
由于在充电设施运营商和政府分别主导的博弈均衡中,博弈均衡点总是偏向主导博弈方,而另一博弈方的利益却受损,这样的博弈均衡很难被双方接受,博弈谈判很可能破裂。出现这种情况主要是由于电动汽车发展初期电动汽车及充电设施建设成本较高,政府必须给予充电设施运营商适当的政策支持或补贴支持,本文假设政府给予充电设施运营商的补贴最高为SEmax=10%。
3.2节和3.3节分析表明,无论哪一方作为博弈主导方,电池价格对充电定价和汽车数量都影响较大,故对电池价格进行单独分析。假设电池价格每年下降0.14元/(W·h)时,得到均衡结果见表6。充电设施运营商达到盈亏平衡时,充电电价定价为0.881 4元/(kW·h),充电电价上涨0.12%。到2020年私人乘用汽车保有量为34.07万辆,汽车数量减少15.52%。电动汽车达到40万辆时充电电价定价为0.705 9元/(W·h),充电电价下降20.56%。到2020年充电设施运营商累计收益为-5.46亿元。
假设电池价格平均每年的下降幅度为0.26元/(W·h)时,充电设施运营商达到盈亏平衡时,充电电价定价为0.879 1元/(W·h),充电电价下降0.14%;到2020年私人乘用汽车保有量为49.36万辆,汽车数量增加22.36%。充电设施运营商实现盈亏平衡时,电动汽车达到49万辆,充电电价定价为0.880 0元/(W·h),充电电价下降0.96%。到2020年充电设施运营商累计收益为0.035亿元。
在政府给予充电设施运营商适当的补贴情况下,电池价格下降幅度调整±2%后,充电设施运营商的累计收益和电动汽车保有量随充电电价的关系如图8所示。当电池价格每年下降0.14元/(W·h),博弈均衡时,政府主导时的充电电价小于充电设施运营商主导时的电价,均衡结果很难为双方接受。而当电池价格每年下降0.2元/(W·h),政府主导博弈的充电电价大于充电设施运营商主导的博弈均衡电价,此时双方设定的充电电价都可以为双方接受。经过计算可得到,当电池价格平均每年的下降幅度为0.197 3元/(W·h)时,可实现双方的博弈目标一致,即车辆保有量可达到40万辆、充电设施运营商可实现盈亏平衡,此时充电定价为0.879 7元/(kW·h),则不管博弈双方哪一方作为主导方都不会损害另一方的利益,从而可以达到双方可接受的博弈均衡解。
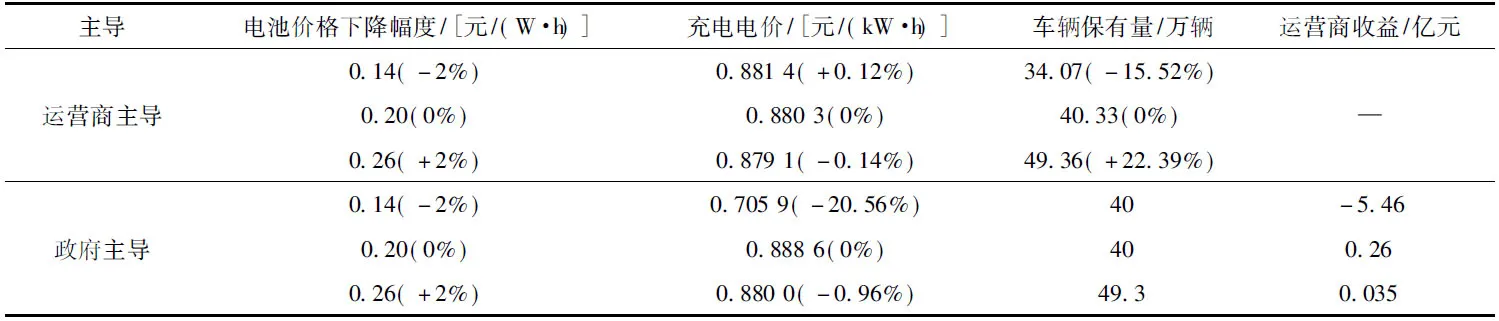
表6 电池价格下降幅度调整后的均衡结果Tab.6 The balanced result when the drop rate of battery price adjusted
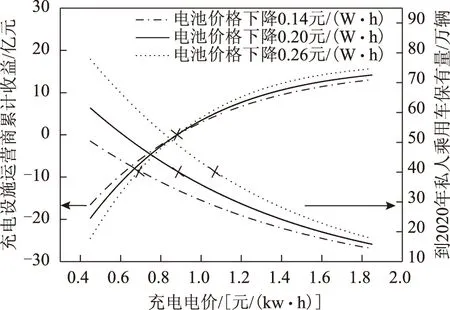
图8 运营商收益和车辆保有量随各影响因素变动幅度变化±2%的关系Fig.8 The curves of accumulated earnings and private EV holdings along with±2% change of amount of variation of various influencing factors
假设传统汽车可使用15年(运行30万km),根据过去8年的统计结果,预测汽油价格平均每年增长2.5%。以当前的电动汽车的质保期限为依据,电动汽车电池包质保期为6年,电动汽车每年行驶里程为2万km,假设以后每两年电池质保期限增加一年,本文设定达到质保期限就购置新电池包。如图9所示,2015年购买传统汽车以及使用15年的广义成本为22.14万元,2015年购买电动汽车和2021年更换新的电池包以及使用15年的广义成本为26.49万元,补贴[24]后广义成本为21.74万元。补贴前电动汽车的广义成本高于传统汽车,因此政府为了促进电动汽车产业的发展,鼓励用户购买电动汽车,对用户进行补贴,用户在2015年购买电动汽车时,补贴后电动汽车的广义成本比传统汽车低0.4万元,而且随后几年电动汽车的广义成本都逐渐减少,如用户在2020年购买电动汽车时补贴后电动汽车的广义成本低4.2万元。

图9 15年内广义成本与成本之差随年份的关系Fig.9 The curves of generalized cost and cost variance along with time for 15 years
在长期看来使用电动汽车的广义成本低于传统汽车,但是在短期经济性计算中,比如6年内,如图10所示,补贴前在未来6年里无论哪一年购买电动汽车,其广义成本都高于传统汽车。政府补贴后,只有到2017年购买电动汽车其广义成本才首次低于传统汽车。
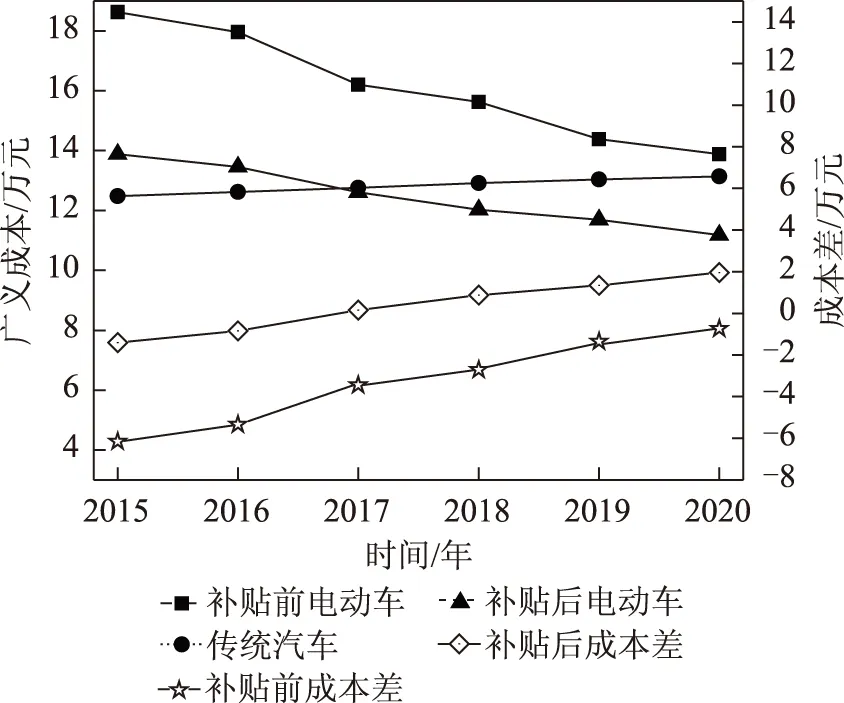
图10 6年内广义成本与成本之差随年份的关系Fig.10 The curves of generalized cost and cost variance along with time for 6 years
从电动汽车长期使用上看,尽管电动汽车使用过程中需要更换一次电池包,但电动汽车使用成本较低,而传统汽车的使用成本较高,因此政府补贴后电动汽车广义成本从2015年起就低于传统汽车。但是从短期使用的角度分析,由于电动汽车的初始购置成本较高,补贴前6年的广义成本在2020年以前都高于传统汽车,补贴后广义成本在2017年首次低于传统汽车。因此,从长期使用的经济学角度看,补贴后购买电动汽车其广义成本总是较低的。
4 结论
运用Logit模型将消费者行为引入到政府与充电设施运营商的博弈模型中,从而确立了涉及三者利益的关于充电电价和电动汽车发展的最终三方博弈模型。基于静态非合作博弈,在以充电设施运营商为主导的博弈中,由于充电设施建设成本直接影响着充电设施运营商的收益,充电设施建设成本下降幅度变动对充电定价影响较大;而电池价格对车辆保有量影响较大,这是因为电池成本在电动汽车总成本中所占的比重较大,直接影响用户购买电动汽车的概率。在政府主导的静态博弈中,电池价格对充电定价和充电设施运营商收益影响较大,电池价格的高低直接决定了用户的广义成本大小,进而决定了电动汽车的市场分担率,而为了实现汽车数量的目标必然会大幅调整充电电价,间接地充电设施运营商的收益也将大幅波动。
在电动汽车发展初期,充电设施建设成本较高,考虑政府给予充电设施运营商适当的补贴,当电池价格平均每年的下降幅度为0.197 3元/(W·h),充电定价为0.879 7元/(kW·h),博弈均衡时充电设施运营商和政府都可达到各自的目标,而用户也可在6年使用期内于2017年实现油电持平。从长期(15年)使用的角度测算分析,用户使用电动汽车的广义成本总是低于传统汽车,在2015年购买电动汽车用户收益为0.4万元,在2020年购买电动汽车时用户收益为4.2万元。因此各方应该加强对电池的研发及相关产业的投入,推动电池性能的提升和电池价格的下降。基于静态非合作博弈,充分考虑博弈各方的利益和策略,合理地制定充电电价,以符合电动汽车发展的实际情况,将有力地促使电动汽车的大规模推广应用。
[1] 国务院.节能与新能源汽车产业发展规划(2012—2020年)[S].2012.
[2] 庄莹华,姚丹靖,赵忠平.电动汽车充电价格机制研究[J].华东电力,2014,42(9):1938-1940. Zhuang Yinghua,Yao Danjing,Zhao Zhongping.EV charging price mechanism[J].East China Electric Power,2014,42(9):1938-1940.
[3] 郑颖,孙近文,张冲,等.考虑电动汽车接入的配电系统静态电压稳定裕度研究[J].电工技术学报,2014,29(8):20-26. Zheng Ying,Sun Jinwen,Zhang Chong,et al.Study of voltage stability margin for the distribution network with electric vehicle integration[J].Transactions of China Electrotechnical Society,2014,29(8):20-26.
[4] Peterson S B,Whitacre J F,Apt J.The economics of using plug-in hybrid electric vehicle battery packs for grid storage[J].Journal of Power Sources,2010,195(8):2377-2384.
[5] Gao Bingtuan,Zhang Wenhu,Tang Yi,et al.Game-theoretic energy management for residential users with dischargeable plug-in electric vehicles[J].Energies,2014,7(11):7499-7518.
[6] 戴诗容,雷霞,程道卫,等.分散式电动汽车入网策略研究[J].电工技术学报,2014,29(8):57-63. Dai Shirong,Lei Xia,Cheng Daowei,et al.Study on V2G strategy of distributed electric vehicles[J].Transactions of China Electrotechnical Society,2014,29(8):57-63.
[7] Dai Yue,Chao Xiuli,Fang Shucheng,et al.Pricing in revenue management for multiple firms competing for customers[J].International Journal of Production Economics,2005,98(1):1-16.
[8] Tushar W,Saad W,Poor H V,et al.Economics of electric vehicle charging:a game theoretic approach[J].IEEE Transactions on Smart Grid,2012,3(4):1767-1778.
[9] Ito H.Disturbance and delay robustness guarantees of gradient systems based on static noncooperative games with an application to feedback control for PEV charging load allocation[J].IEEE Transactions on Control Systems Technology,2013,21(4):1374-1385.
[10]滕耘,胡天军,卫振林.电动汽车充电电价定价分析[J].交通运输系统工程与信息,2008,8(3):126-130. Teng Yun,Hu Tianjun,Wei Zhenlin.Analysis on charge price of electric vehicles[J].Journal of Transportation Systems Engineering and Information Technology,2008,8(3):126-130.
[11]张菁菁.电动汽车充电设施建设与发展的多方博弈分析[D].北京:北京交通大学,2011.
[12]金安.LOGIT模型参数估计方法研究[J].交通运输系统工程与信息,2004,4(1):71-75. Jin An.On methodology of parameter estimation in LOGIT model[J].Journal of Transportation systems Engineering and Information Technology,2004,4(1):71-75.
[13]Wu Qiong,Chen Feng,Zhang Guohui,et al.Mixed logit model-based driver injury severity investigations in single-and multi-vehicle crashes on rural two-lane highways[J].Accident Analysis & Prevention,2014,72:105-115.
[14]Manski C K,Mcfadden D.Structural analysis of discrete data with econometric applications[M].Cambridge,MA:Mit Press,1981.
[15]卫振林,张菁菁.区域电动汽车市场推广的综合预测[J].数据采集与处理,2010 (S1):203-206. Wei Zhenlin,Zhang Jingjing.Comprehensive prediction of regional electric vehicle market extension[J].Journal of Data Acquisition & Processing,2010 (S1):203-206.
[16]孙丙香,姜久春,牛军龙,等.基于两种商业模式的动力电池运营价格测算及对比分析[J].高技术通讯,2013,23(3):302-307. Sun Bingxiang,Jiang Jiuchun,Niu Junlong,et al.Measurement and comparative analysis of the operation price of power batteries based on two business models[J].Chinese High Technology Letters,2013,23(3):302-307.
[17]汪贤裕.博弈论及其应用[M].北京:科学出版社,2008.
[18]谢织予.经济博弈论[M].3版.上海:复旦大学出版社,2007.
[19]王丹.博弈论在电力交易和投资中的应用研究[D].青岛:青岛大学,2006.
[20]Saad W,Han Z,Poor H V,et al.A noncooperative game for double auction-based energy trading between PHEVs and distribution grids[C]//2011 IEEE International Conference on Smart Grid Communications,Brussles,2011:267-272.
[21]财政部,科技部,工信部,发改委.关于2016-2020年新能源汽车推广应用财政支持政策的通知[S].2015.
[22]孙丙香,何婷婷,牛军龙,等.基于换电和电池租赁模式的纯电动汽车运营成本评估及预测研究[J].电工技术学报,2014,29(4):316-322. Sun Bingxiang,He Tingting,Niu Junlong,et al.The operational cost evaluation and prognosis of pure electric bus based on battery swap and leasing mode[J].Transactions of China Electrotechnical Society,2014,29(4):316-322.
[23]孙丙香,姜久春,张维戈,等.基于内部收益率法的动力电池租赁价格测算[J].电力系统自动化,2011,35(13):27-30. Sun Bingxiang,Jiang Jiuchun,Zhang Weige,et al.Measurement of the power battery leasing price based on the internal rate of return method[J].Automation of Electric Power Systems,2011,35(13):27-30.
[24]罗剑,王树盛,李旭宏.基于SB分布的 Mixed Logit 交通方式分担模型及其验证[J].公路交通科技,2007,24(6):110-113. Luo Jian,Wang Shusheng,Li Xuhong.Mixed Logit trafic mode split model based on SB distribution and its validation[J].Journal of Highway and Transportation Research and Development,2007,24(6):110-113.
Quantitative Analysis of Influence Factors about EV’s Charging Electricity Price Based on the Static Non-Cooperative Game Theory
Sun Bingxiang1,2Ruan Haijun1,2Xu Wenzhong1,2Jiang Jiuchun1,2Gong Minming1,2
(1.National Active Distribution Network Technology Research Center Beijing Jiaotong University Beijing 100044 China 2.Collaborative Innovation Center of Electric Vehicles in Beijing Beijing Jiaotong University Beijing 100044 China)
The forthcoming mass popularization and application of electric vehicles(EVs)would prompt the urgent requirement of reasonable charging electricity price.Game theory is used to analyze the interests relationship of the main three players to the EV’s development including the government,the charging infrastructure operator and the users.Then,the tripartite game model about the charging electricity price and holdings of EVs is built and gets classical solution on the basis of static non-cooperative game.Focusing on EV’s data of nine cities in the Pearl River Delta,the game equilibrium solutions are obtained based on charging infrastructure operator or the government as the leading party respectively. Moreover,the variations of charging electricity price,EVs holdings and the sensitive degree of five influence factors are quantitatively calculated.Ultimately considering the acquired appropriate subsidies of charging infrastructure for the operator offered by government,the accepted game equilibrium solution for both players is produced and the generalized cost of the user is analyzed,which can satisfy the interests of three players. It is beneficial to large-scale proliferation of EVs.
Electricity vehicle holdings,charging electricity price,static non-cooperative game
国家电网公司科技资助项目(E15L00190)。
2015-06-17 改稿日期2015-11-04
TM911
孙丙香 女,1979年生,博士,副教授,研究方向为动力电池成组应用技术。
E-mail:bxsun@bjtu.edu.cn(通信作者)
阮海军 男,1989年生,博士研究生,研究方向为动力电池成组应用技术。
E-mail:14117386@bjtu.edu.cn
