基于普通精度增量式编码器的永磁伺服电机低速检测与控制优化方法研究

汪兆栋 文小琴 游林儒 黄招彬

(华南理工大学自动化科学与工程学院 广州 510640)



基于普通精度增量式编码器的永磁伺服电机低速检测与控制优化方法研究

汪兆栋 文小琴 游林儒 黄招彬

(华南理工大学自动化科学与工程学院 广州 510640)

针对永磁同步伺服电机传统控制方法的缺点，提出了一种基于普通精度增量式编码器的低速检测与控制优化方法。在普通低速区，该方法通过扩展M/T法来提高速度检测精度；在超低速区，采用一种改进的T法进行闭环跟踪反馈以实现高精度的速度检测，同时，采用参考速度自适应的PI控制方法，从而获得较好的速度控制性能。最后，在DSP控制器和永磁无刷伺服电机上进行了实验，实验结果表明，所提的优化策略提高了系统低速时的动态性能，扩展了系统的调速范围。

永磁伺服电机 增量式编码器 扩展M/T法 自适应PI控制器 超低速

0 引言

近年来，交流伺服系统已广泛应用于工业领域及日常生活中，包括工业机器人、数控机床、电动汽车等。交流伺服系统的性能主要取决于其定位精度和动态响应，因而在低速时需要很高的转子位置和速度检测精度，在低速时提高转子速度检测精度、减少检测滞后具有很重要的研究意义。为此，要实现高性能的伺服控制和精确检测，伺服系统通常采用高分辨率的编码器。然而，这些高精度的编码器价格昂贵，无法应用在高性价比的系统上。而无传感器控制技术无法确保在低速或零速时的检测精度和控制性能。因此，考虑到成本因素，针对普通分辨率编码器的永磁伺服系统，提出了一种优化的低速检测与控制方法，以提高其在低速范围内的速度检测与控制性能。

对于带增量式编码器的交流伺服系统，由于在高速时M法的速度检测相对误差小于T法，而在低速时M法的速度检测相对误差高于T法，因此，进行速度检测时，一般在高速采用M法、低速采用T法。然而，由于在低速范围内T法的速度检测滞后要比M法的大很多，在低速时采用T法会严重影响到伺服系统的动态性能及稳定性能。当采用一般精度的增量式编码器时，在超低速范围内，其速度检测性能会更差。因此，迫切需要研究一种有效的速度检测与控制方法。

当伺服电机运行在超低速范围内时，即在每个速度检测周期内无法保证检测到一个编码器脉冲信号，那么在系统控制时就有多个不可控的检测周期。文献[1]在低速时提出了一种改进的M法，该方法具有较好的抗干扰性能，但仍有较大的检测误差与滞后。针对这些不可控的检测周期，文献[2]提出了一种基于线性数学模型的多项式外插法，以改善伺服系统的动态性能，包括速度一阶预估法和速度二阶预估法。然而，由于在低速时滞后时间较长、误差较大，导致系统运行不稳定，甚至不停地来回抖动，在此情况下，加速度和加加速度[2]会无序地变化，这极大地限制了线性预估法的估计效果。文献[3，4]分别提出了基于载波频率成分、基于中心差分滤波算法的无传感器控制方法。针对在低速时的无传感器控制，文献[5-12]提出了基于电机模型的无传感器位置与速度估计方法，如高频信号注入法[5，6]、反电动势法[7，8]、滑模观测器[9-12]。这些无传感器方法能实现在低速时的速度检测，但其信噪比较差，估计误差较大。如反电动势观测器易受逆变器非线性影响，在低速时低精度的电流会抑制观测性能，而高频注入法会引入更多的电流谐波和转矩脉动。此外，所有的无传感器方法都没有充分利用其编码器信号，造成了有效资源的浪费。

由于多项式外插法和无传感器控制方法在低速时控制性能较差，文献[13-19]提出了一种基于编码器信号的转子位置和速度估算方法：文献[13]利用编码器信号修正估计误差来改进反电动势观测器；文献[14]在编码器位置检测基础上，提出了一种龙伯格状态观测器，但由于编码器位置检测时的高频噪声，该方法效果不好；文献[15]提出了一种矢量跟踪观测器以提高其鲁棒性；文献[16，17]在低精度传感器控制下，通过一种谐波解耦的矢量跟踪观测器方法，提高了低速时的检测性能，但该方法仅适用于高速伺服系统中。在普通精度传感器作用下，文献[18]提出了一种基于估计速度反馈的矢量跟踪观测器方法。为了校正固有的速度误差，文献[19]在平均转子速度前馈控制作用下，基于矢量跟踪位置观测器上修改了反电动势。综上所述，这些基于编码器检测的观测器方法能够充分利用现有资源与信息，具有较好的速度估算效果，但这些算法都很复杂，其数字控制器较难实现。

为了提高低速范围内的转子速度检测与控制性能，在编码器信号和优化的速度控制器的基础上，将速度检测与速度控制相结合，提出了一种优化的速度检测与控制方法，其超低速控制效果能够得到改善。在普通低速区，即编码器脉宽小于检测周期，采用一种扩展M/T法来提高速度精度，从而提高系统的动态性能；在超低速区，即编码器脉宽大于检测周期，根据速度检测滞后，在改进的T法反馈基础上，采用一个自适应的PI速度控制器进行调节。采用上述复合控制方法，可实现在普通低速和超低速时的高性能控制。最后，通过一台永磁无刷伺服电机进行了实验验证，且速度检测与控制性能都在普通低速和超低速时分别被评估。实验结果表明，所提的优化控制策略扩展了系统的调速范围，提高了系统低速时的动态性能。

1 低速时的速度检测

高性能伺服系统要求在宽调速范围内具有高精度的转子位置与速度检测，高精度编码器价格昂贵，大大增加了系统的成本。因此，在性价比较高的普通精度增量式编码器(通常1 000～5 000线/转)基础上，提高伺服系统检测精度与控制性能，非常有研究价值。

在交流伺服系统中，传统的速度检测方法有M法和T法。M法在高速时有较高的速度精度，而T法在低速时有较好的分辨率。然而，它们都有各自的缺陷，如M法有固定的速度检测滞后，而T法有较长的检测相位滞后。在此，对两种方法进一步深入研究，从而提高在低速时的速度检测性能。

1.1 传统的速度检测方法

在传统的速度检测方法中，一般通过DSP的捕获单元CAP和正交编码器脉冲单元QEP来检测编码器脉冲数量和时间间隔。记M法的速度检测周期为Ts， 用于检测编码器脉冲时间间隔的高频时基为Tcap， 设增量式编码器的分辨率为Nppr， 那么一个脉冲代表2π/N的角位移。记当前检测周期和下一个检测周期内的编码器脉冲数分别为Mn、 Mn-1， 那么在检测周期内用于计算角位移的编码器脉冲数为Mn-Mn-1， 通过M法检测的角速度可表示为

(1)

记最新的脉冲间隔为Tn=MpTcap， 其中Mp为脉冲定时器的值，则通过T法检测的角速度可表示为

(2)

因此，随着速度下降，绝对检测误差和相对检测误差都会减小，而检测延迟将增加到约一个脉冲间隔。此外，由于脉冲定时寄存器有上界，脉冲时间间隔有上限，通过T法测量到的速度不能无限低。对这两种方法的性能进行对比分析，如图1所示。在高速时，T法的相对速度误差远高于M法，而在低速时则刚好相反。然而，在低速时，随着速度下降，T法的速度检测延迟越来越长于M法。从图1可知，有两个临界速度，即检测临界速度ωdc和可控临界速度ωcc， 分别为237r/min和7.5r/min。

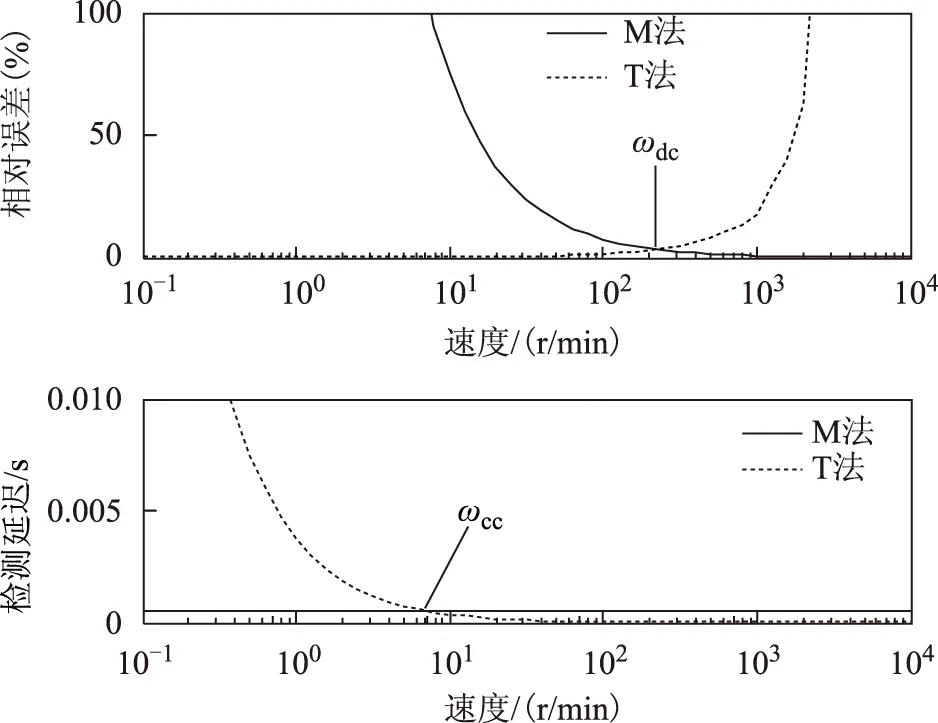
图1 M法和T法的速度检测误差和延迟Fig.1 The speed detection relative error and delay for M-method and T-method

1)检测临界速度：当ΔωMpu=ΔωTpu，M法和T法的相对检测误差相等；当ω>ωdc，M法的相对检测误差较小；当ω<ωdc，T法的相对检测误差较小。

2)可控临界速度：当Tn=Ts时，M法和T法的检测延迟相等，即检测周期等于脉冲时间间隔；当ω>ωcc， 在每个检测周期内，速度是可测可控的；当ω<ωcc， 在某些检测周期内，速度是不可测不可控的。

为了解决在全速范围内的速度检测与速度控制问题，根据可控的临界速度ωcc， 速度可分为两部分。当速度大于ωcc时，为正常的速度范围，此时Tn≤Ts， 且每个检测周期至少包含一个编码器脉冲信号，因此转子速度是可控可测的。根据检测临界速度ωdc， 正常的速度范围又可细分为3部分，包括高速范围、中速范围和普通低速范围。当速度小于ωcc时，为超低速范围，此时Tn>Ts， 且在每个检测周期内包含少于一个编码器脉冲信号，因此在超低速时有很多不可测不可控的检测周期。总之，可将速度范围分区如下：

1)Tn≤Ts， 即正常的速度范围，ω>ωcc。 正常的速度范围又分为：高速范围，即ω>ωdc； 中速范围，在ωdc附近，即ω≈ωdc； 普通低速范围，即ωcc<ω<ωdc。 2)Tn>Ts， 即超低速范围，ω<ωcc。

1.2 正常速度范围内的速度检测

在正常速度范围内，通常采用传统的M/T法来检测速度。当实际速度高于检测临界速度时，采用M法；反之，则采用T法。图2a、图2b分别为普通低速和超低速时编码器信号检测的时间展开图。其中，Tn/Tn-1、tR/tR(n-1)分别为当前/下一个检测周期内最近的脉冲时间间隔和头尾部分的不完整脉冲，Mn/Mn-1为当前/下一个检测周期内的编码器脉冲数。在传统的M/T法控制下，其速度检测可表示为

(3)

通常，在检测临界速度附近，M法和T法之间需要不断切换使用，造成传统的M/T法在中速范围性能较差。而且，在普通低速时，传统M/T法的绝对检测误差也较大。因此，为了提高在正常速度范围内的速度检测性能，提出了一种扩展M/T法，可使其平均速度计算更为精确，如式(4)、式(5)所示。

(4)

(5)

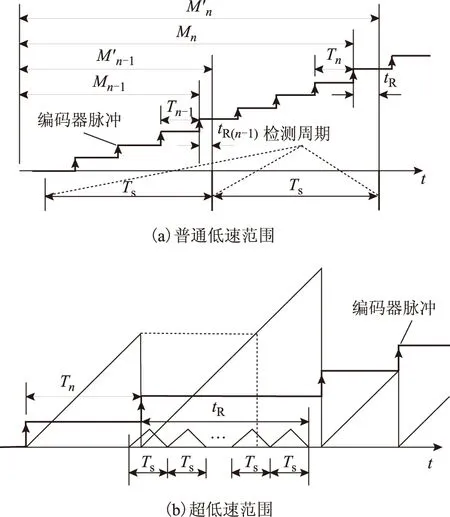
图2 低速时编码器信号检测的时间展开图Fig.2 Encoder signal detection time expansion plan at low speed range

显然，在扩展M/T法中，将这个不完整的脉冲tR考虑在内，可得到改进的脉冲数目，当系统采用扩展M/T法时，其效果在高速时如M法，而在低速时如T法。因此，扩展M/T法不需要区分高速、低速区间，有效地解决了M法与T法之间切换时带来的问题。在正常的速度范围内，该方法控制效果好，只有半个检测周期的滞后，即Ts/2。

然而，在超低速时，采用扩展M/T法会存在一些问题。由于在每个检测周期内检测不到一个脉冲信号，此时速度计算基本上取决于tR， 这导致脉冲间隔易受其影响而变化。如果速度变化再大些，那么该方法将不再有效。总之，扩展M/T法在正常速度范围内能够提高速度检测精度，但其在超低速时无法检测速度。因此，有必要研究在超低速时的速度检测优化问题。

1.3 在超低速时的速度检测

在超低速范围内，需要多个检测周期才能检测到一个编码器脉冲，这意味着有很多个不可测不可控的周期，如1.2节所述，此时扩展M/T法将无法适用。为此，有学者在线性数学模型的基础上，提出了多项式外插法，包括速度一阶/二阶预估器。然而，由于较长的速度检测延迟和较大的误差，伺服系统无法运行稳定，在超低速时甚至偶尔会向反方向运动，造成加速度与加加速度混乱无序，这将严重影响线性预估法的估计效果。因此，在超低速时，速度检测还是选择传统的T法进行控制，但此时的T法需要做一定的改进，以加快其动态响应。如图2b所示，在超低速时，按式(6)计算速度。当在多个检测周期内检测不到编码器脉冲时，这个非整数脉冲tR将远长于最新的脉冲间隔，这意味着伺服系统大大减速。因此，在实际脉冲信号产生之前，采用tR计算速度，这样可获得一个更快的速度响应。

(6)

在经典的矢量控制中，最新的平均速度通常被用来参与速度反馈控制。然而，当伺服系统在超低速区域运行时，通过改进的T法检测到的平均速度仍会有较长的检测延迟，这将会导致速度在某些周期内无法控制，从而降低了速度动态性能。因此，为了获得较好的控制性能，在超低速时需要对控制策略进行优化。

2 低速时的速度控制

2.1 速度控制器设计

转子磁链定向控制通常应用到永磁同步电机位置/速度伺服控制系统中，速度控制伺服系统的等价数学模型被简化，如图3所示。其中，ω*和ω分别为标幺化的参考速度和实际输出速度(通过额定速度来标幺)。

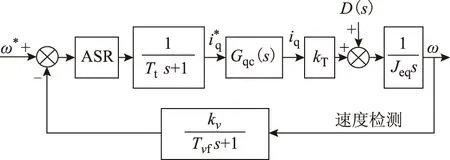
图3 速度控制环Fig.3 Speed control loop

(7)

式中，ki为电流归一化系数(额定电流峰值的倒数)；T∑i为总电流环滞后，包括离散电流控制器延迟、电源模块输出延迟和电流检测延迟。当摩擦忽略不计时，速度环的开环传递函数可表示为

(8)

因此，速度控制环总的延迟为

T∑v=Tvctrl+Tt+2T∑i+Tvf

式中，Tvctrl为离散的速度控制器延迟(和速度控制周期相等)。

假定λ是中频带宽(通常设为3～10倍)，那么速度控制器的积分时间Tiv可设置为Tiv=λT∑v， 根据最小峰值闭环幅-频特性规则，速度环增益可设计为

(9)

通过上述方法，可设计一个优化的速度控制器来实现伺服速度环的高性能控制。

2.2 速度检测与控制策略

由上述分析可知，在超低速时，采用传统的T法能获得较高的速度检测精度，但却有较长的检测滞后，当速度下降时，虽然采用改进的T法能减少其检测滞后，但仍不能完全消除。通常，在超低速时，随着速度减小，检测滞后Tvf会随之增大，导致总的速度环滞后T∑v也会增大，如果还是采用固定PI控制器，那么速度环的稳定性和动态性能就会比较差。因此，需要根据速度检测滞后来设计自适应PI控制器，这样可获得一个更好的控制效果。

在超低速时，检测延迟主要取决于反馈编码器脉冲的时间间隔(忽略编码器自身和其信号调理电路的相位滞后)。然而，在速度调节趋于稳定前，脉冲时间间隔会不断剧烈变化，造成系统不稳定。因此，根据参考速度，其速度检测滞后大致可以计算出。换言之，在超低速时可采用一种随参考速度变化的自适应PI控制器。

在正常速度范围内，采用扩展M/T法，其速度检测总有一个固定的平均检测延迟(Ts/2)，随着速度变化，其总的速度环滞后也保持不变。因此，在正常速度时采用固定的PI控制器能满足控制性能要求。

综上所述，在超低速时，采用改进的T法和自适应PI控制器是一种优化的选择；而在正常速度时，采用扩展M/T法和固定PI控制器能获得较好的性能。所提的速度检测与控制策略可总结如下：

1)在正常的速度范围(Tn≤Ts， 在ωcc之上)：扩展M/T法用于速度检测；固定PI控制器用于速度控制。

2)在超低速范围(Tn>Ts， 在ωcc之下)：改进的T法用于速度检测；自适应PI控制器用于速度控制。

3 实验研究

3.1 实验平台

为了验证所提方法的可靠性和优越性，搭建了一个永磁伺服系统的实验平台，如图4所示，并进行了一系列实验研究。在实验中，DSP控制器是TMS320LF28035，IGBT模块是7MBR100U4B-120，电机是三洋永磁无刷伺服电机，型号是P50B08075DXS00，其参数见表1。其中，电气时间常数、机械时间常数分别为5.8ms、1.2ms，说明伺服电机本身有快速的响应性能。此外，增量式编码器为2 000线/转，通过QEP四倍频，伺服系统可完成N=8 000线。此外，控制器与PC机之间通过USB-CAN接口来实现通信(波特率设置为1 MHz)，Labview软件用于实时监控运行状态。

图4 实验平台Fig.4 Experimental platform

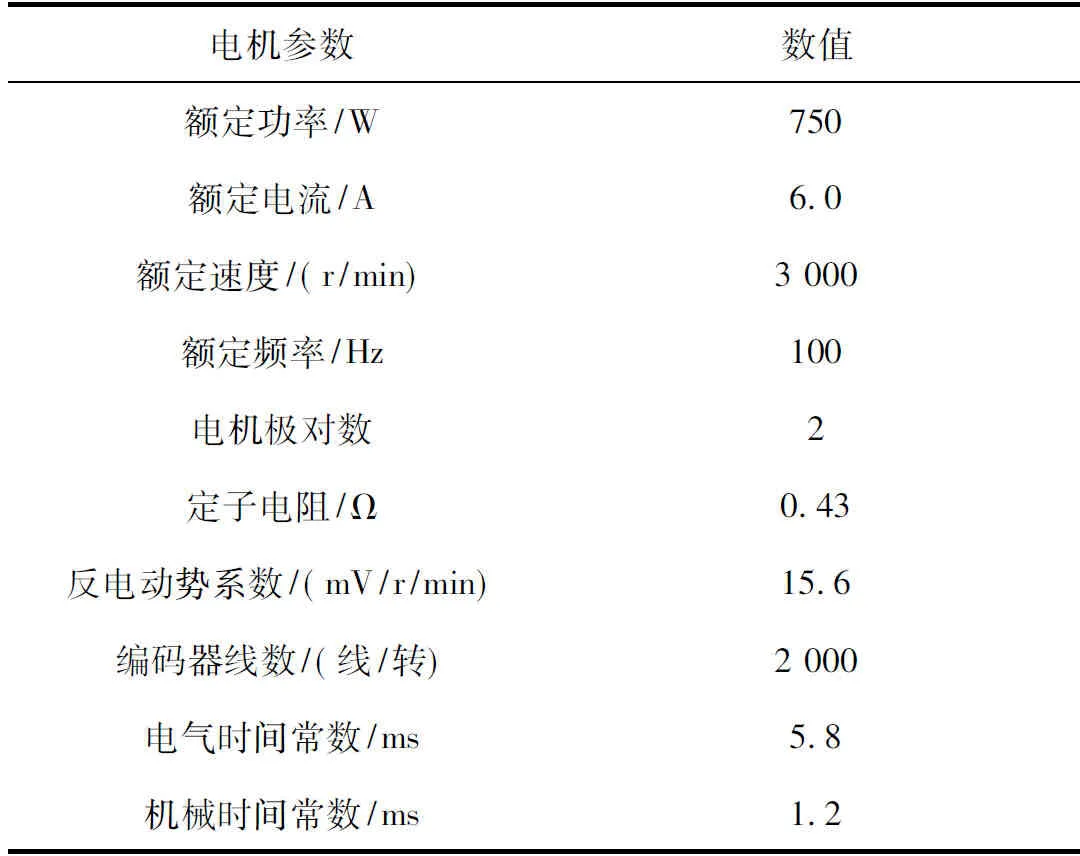
表1 永磁无刷伺服电机参数Tab.1 The PMBSM parameter

在实验中，永磁无刷伺服电机按id=0进行矢量控制，PWM载波频率设置为10 kHz，高频时基为Tcap=1 μs， 可控的临界速度为ωcc=0.25 Hz，检测临界速度为ωdc=7.9 Hz。因此，超低速范围为ω<ωcc=0.25 Hz，而正常的低速速度范围为ω<ωcc<ωdc， 即从0.25 Hz到7.9 Hz。在很多伺服应用场合，起动时的负载通常比较轻，同时考虑到测试方便性，本文速度控制实验是在轻载情况下进行测试的(30%额定负载)，而速度检测实验是在空载下进行的。

3.2 普通低速时的速度检测/控制评估

为了验证扩展M/T法的优越性，在普通低速时进行了一系列的比较试验。在实验中，采用T法进行速度闭环跟踪控制，并且3种检测方法(M法、T法和EMT法)都检测伺服速度。在0.100 Hz、0.25 Hz、0.500 Hz、1.00 Hz、2.00 Hz、4.00 Hz六个不同频率点对速度检测性能进行评估，每个频率的测试都保存了足够多的检测数据(每个检测周期1 ms有一个检测结果)。

图5为在100 ms内3种方法在6个不同运行频率时的实验结果。在频率为4.00 Hz处，采用EMT方法检测，伺服电机运行相对较稳定，波动最小，检测性能最好，而T法波动最大，M法介于两个方法中间；在频率为2.00 Hz和1.00 Hz处，EMT法仍有最平滑的检测结果；在频率为0.50 Hz和0.25 Hz处，EMT法和T法检测效果基本相同，都优于M法。由此可见，在普通低速范围内，EMT法具有良好的检测性能。然而，当实际速度接近可控临界速度或更低时，以图5中0.10 Hz为例，由于在每个检测周期内无法检测到1个脉冲，因此EMT法也无法正常检测速度。由此可见，EMT法在普通低速时有很多优点，如速度波动小、检测精度高、电机运行较平滑，而在超低速时，该方法不再适用。

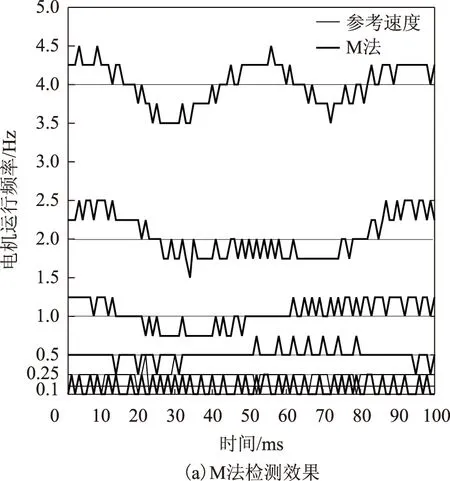
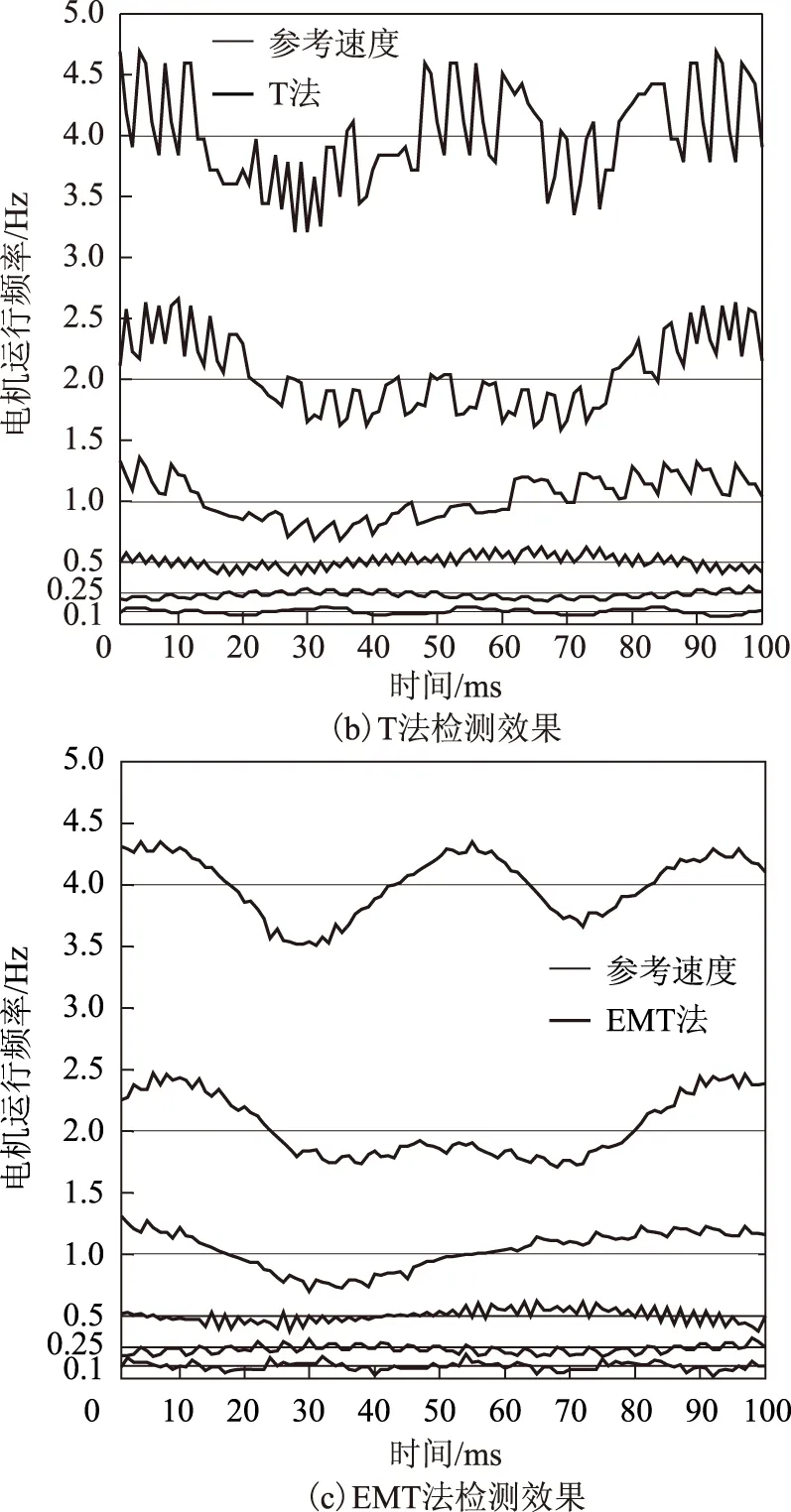
图5 普通低速固定PI检测效果对比图Fig.5 Detection effect comparison diagram for constant PI at ordinary-low speed

为了更好地说明这3种方法在普通低速时的控制性能，在6个不同频率处进行了阶跃响应，其控制效果如图6所示。在频率分别为4.00 Hz、2.00 Hz、1.00 Hz处，3种方法的控制效果相差不大，EMT法的相对更好些；在频率分别为0.50 Hz、0.25 Hz、0.10 Hz处，EMT法超调量最大，调节时间较长，而T法的超调量最小，调节时间最短，且速度波动很小，其稳态误差最小。因此，在普通低速时，采用EMT法比较合适，而在超低速时，EMT法不再适用，采用T法控制效果相对更好些。

由上述分析可知，在普通低速范围内，EMT法的速度检测性能优于M法和T法。因此，在普通低速时采用EMT法能提高伺服系统的速度检测精度，但建议在超低速时不要采用EMT法。

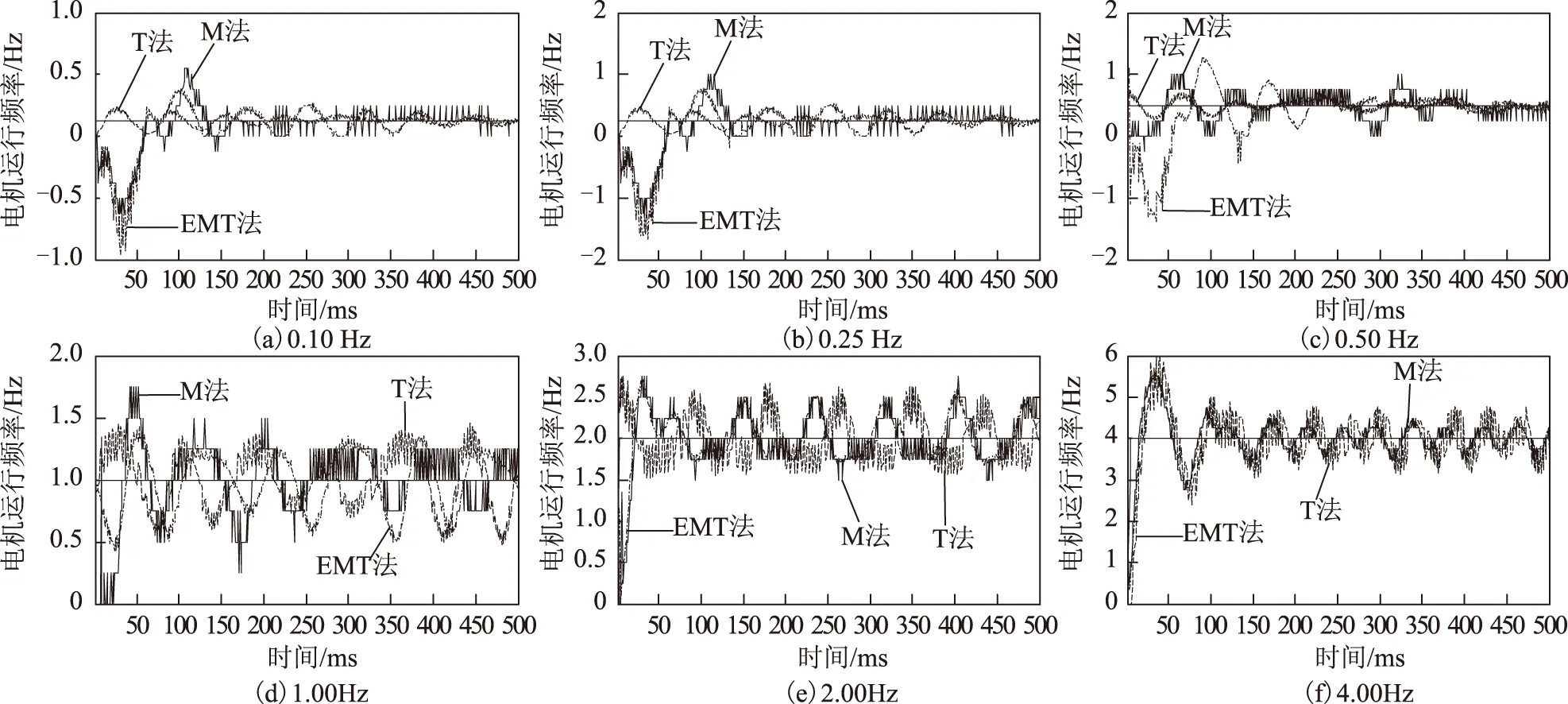
图6 普通低速固定PI控制效果对比图Fig.6 Control effect comparison diagram for constant PI at ordinary-low speed

3.3 在超低速时的速度控制评估

为了验证伺服系统在超低速时的速度控制性能，在ω<0.25 Hz时，采用一种改进的T法闭环跟踪反馈进行速度检测，并采用两种类型的PI控制器进行速度控制，即固定PI控制器(CPI)和自适应PI控制器(API)，如图7所示。

考虑到在超低速时负载转矩和轴摩擦因素的影响，在不同频率下(0.01 Hz、0.02 Hz、0.05 Hz)进行了多个实验，且实验选择在相同的电机段(起点和终点一样)进行，这样就确保了电机在运行时能够保持外部条件一致。因此，在图7所示的实验结果中，存在近似的转矩电流轮廓曲线。

为了比较在相同频率处两种PI控制器的控制性能，可求得最大值、最小值、标准差和速度波动指标，见表2。显然，标准差越小，速度波动指标越小，则说明相应的PI控制器控制性能越好。

从图7a和图7b中可获取自适应PI控制器和固定PI控制器作用下的控制效果。显然，前者的控制效果优于后者，且由表2可知，相比于固定PI控制器，自适应PI控制器具有一些优势，如速度波动更小、速度响应更快、伺服系统稳定性更好。此外，在自适应PI控制器作用下，伺服系统甚至能够稳定运行在0.01 Hz，且其速度波动也在允许的范围内。因此，可调的速度范围高达10 000∶1 (频率从0.01 Hz到100 Hz，即速度从0.3 r/min到3 000 r/min)。

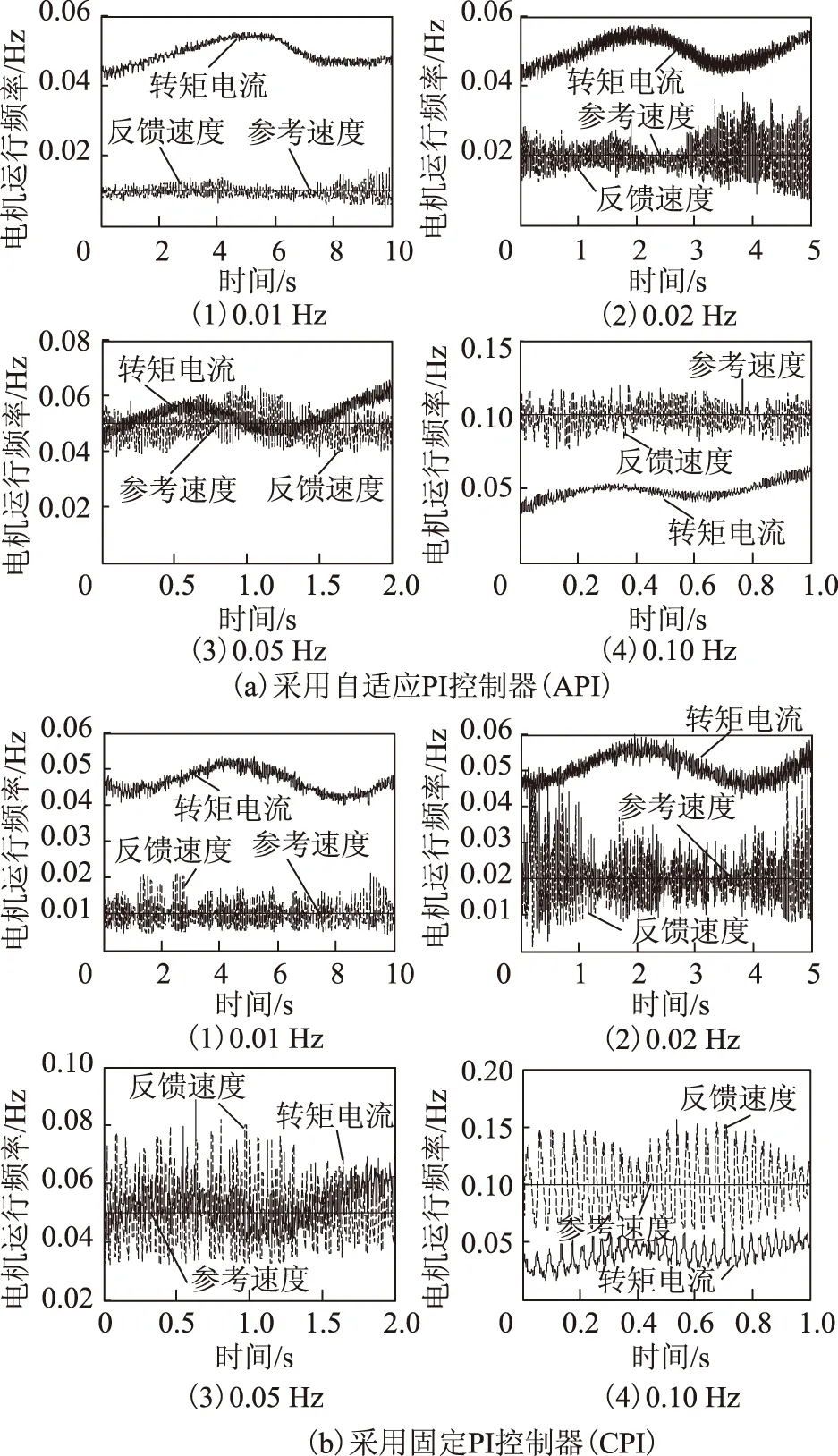
图7 超低速时采用不同PI控制器的速度控制性能Fig.7 Speed control performance for different PI controller at ultra-low speed

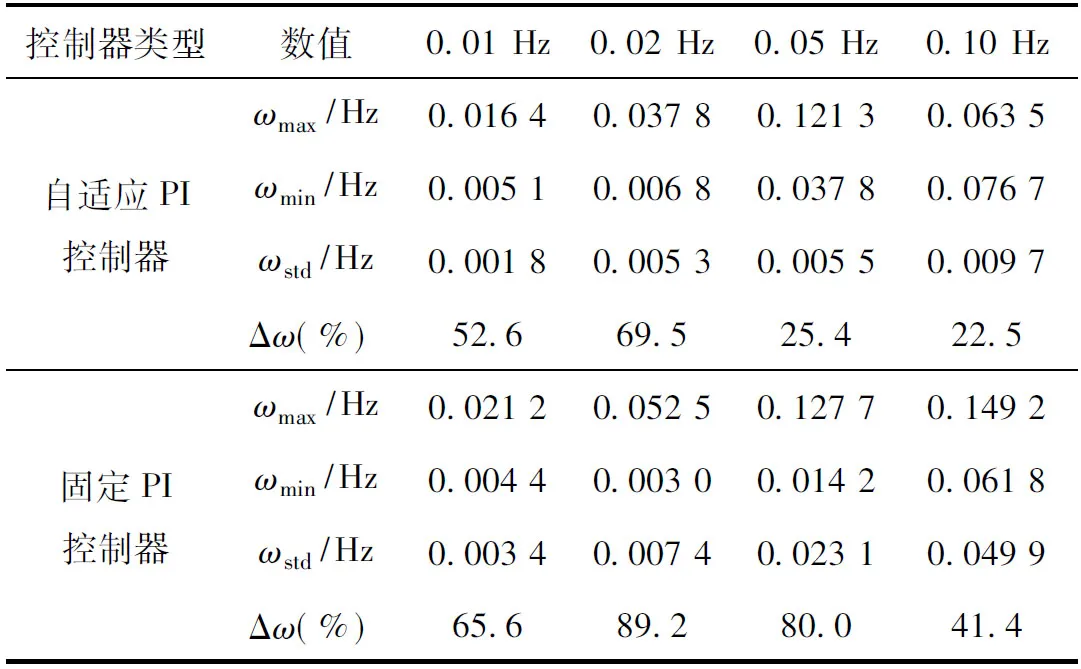
表2 速度波动分析Tab.2 The speed fluctuation analysis

3.4 全速范围内的速度控制

为了验证所提策略在低速时的优越性，在普通低速范围和超低速范围内进行了相关实验，如实验一所述。此外，还进行了两个其他的比较实验(固定PI控制T法反馈和固定PI控制M法反馈)，这些连续实验是在1.00 Hz—0.25 Hz—0.05 Hz下切换进行的。这3个实验如下所述：

实验一：在频率为1 Hz时，采用EMT法进行速度检测，固定PI(Kp=30、Ki=8.5 ms)进行速度控制；而在频率分别为0.25 Hz、0.05 Hz时，采用改进的T法进行速度检测，自适应PI控制器进行速度控制。

实验二：在频率分别为1.00 Hz、0.25 Hz、0.05 Hz处，均采用T法进行速度检测，固定PI(Kp=30、Ki=8.5 ms)进行速度控制。

实验三：在频率分别为1.00 Hz、0.25 Hz、0.05 Hz处，均采用M法进行速度检测，固定PI(同实验二)进行速度控制。

实验结果如图8所示。从图8可看出，在整个低速范围内，采用M法反馈固定PI控制器时，其速度跟踪性能都较差；采用T法反馈固定PI控制器时，在频率为1.00 Hz处速度无法跟踪，在频率为0.25 Hz处跟踪效果和所提方法差不多，而在频率为0.05 Hz处跟踪效果较好，但相比所提方法略差；采用本文提出的优化控制策略，在整个低速范围内，其速度跟踪性能相对都较好。

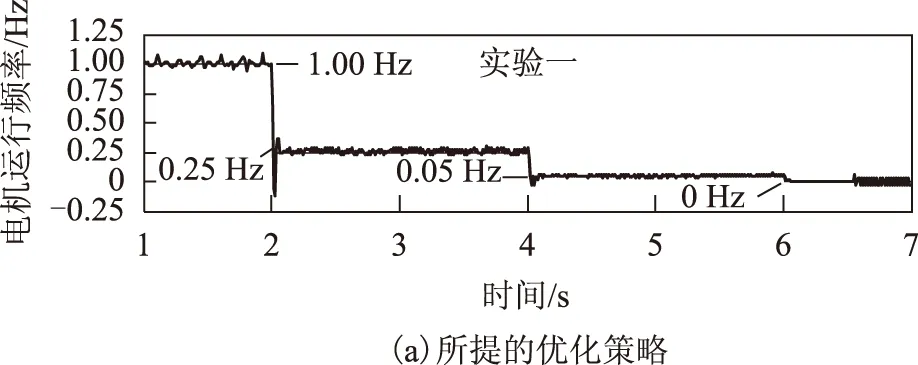
图8 在全低速范围内的速度跟踪性能Fig.8 Speed tracking performance at low speed range

4 结论

本文研究了传统的(带普通精度增量式编码器)速度检测方法，找出了它们的缺陷，并提出了一种扩展M/T法，该方法在正常速度范围内可提高速度检测精度，尤其在普通低速范围时。然后，在超低速时，通过改进传统的T法，减少了速度检测延迟。为了获得在整个低速范围内更好的速度控制性能，在超低速时采用自适应PI控制器，在正常速度时采用固定PI控制器。最后，将所提的速度检测和控制策略应用在一个永磁无刷伺服控制系统上，并对其速度检测与控制性能进行了实验和评估。实验结果和评估结果表明，在正常速度范围内，扩展M/T法具有较高的速度检测精度；在超低速范围内，改进的T法具有较快的速度响应，自适应PI控制具有较好的稳定性能。本文所提的优化策略提高了系统在低速时的动态性能，且将可调的速度范围扩大到了10 000∶1。

[1] Yang Yeepien，Ting Yiyuan.Improved angular displacement estimation based on Hall-Effect sensors for driving a brushless permanent magnet motor[J].IEEE Transactions on Industrial Electronics，2014，61(1)：504-511.

[2] 黄招彬.永磁同步电梯曳引系统的性能优化方法研究：[D].广州：华南理工大学，2014.

[3] 朱军，田淼，付融冰，等.基于载波频率成分的永磁同步电机转子定位研究[J].电力系统保护与控制，2015，43(14)：48-54. Zhu Jun，Tian Miao，Fu Rongbing，et al.Research on rotor position of permanent magnet synchronous motor based on carrier frequency component[J].Power System Protection and Control，2015，43(14)：48-54.

[4] 安小宇，崔光照，丁国强，等.基于中心差分滤波算法的PMSM无传感器控制方法[J].电力系统保护与控制，2013，41(23)：37-42. An Xiaoyu，Cui Guangzhao，Ding Guoqiang，et.al.The PMSM’s sensorless vector control method based on CDKF algorithm[J].Power System Protection and Control，2013，41(23)：37-42.

[5] Yang Shihchin，Lorenz R D.Surface permanent magnet machine self-sensing at zero and low speeds using improved observer for position，velocity，and disturbance torque estimation[J].IEEE Transactions on Industry Applications，2012，48(1)：151-160.

[6] 王高林，杨荣峰，李刚，等.基于高频信号注入的IPMSM无位置传感器控制策略[J].电工技术学报，2012，27(11)：62-68. Wang Gaolin，Yang Rongfeng，Li Gang，et al.Position sensorless control strategy of IPMSM based on high frequency signal injection[J].Transactions of China Electrotechnical Society，2012，27(11)：62-68.

[7] Hejny R W，Lorenz R D.Evaluating the practical low speed limits for back-EMF tracking based sensorless speed control using drive stiffness as a key metric[J].IEEE Transactions on Industry Applications，2011，47(3)：1337-1343.

[8] 李凤祥，徐浩，袁野，等.无刷直流电机无位置传感器转子位置辨识策略[J].电工技术学报，2014，29(12)：107-112. Li Fengxiang，Xu Hao，Yuan Ye，et al.Rotor position identification strategy of brushless DC motors[J].Transactions of China Electrotechnical Society，2014，29(12)：107-112.

[9] Qiao Zhaowei，Shi Tingna，Wang Yindong，et al.New sliding-mode observer for position sensorless control of permanent magnet synchronous motor[J].IEEE Transactions on Industrial Electronics，2013，60(2)：710-719.

[10]朱瑛，程明，花为，等.基于滑模变结构模型参考自适应的电气无级变速器无传感器控制[J].电工技术学报，2015，30(2)：64-72. Zhu Ying，Cheng Ming，Hua Wei，et al.Sensorless control for electrical variable transmission based on sliding mode model reference adaptive system[J].Transactions of China Electrotechnical Society，2015，30(2)：64-72.

[11]陆婋泉，林鹤云，冯奕，等.永磁同步电机无传感器控制的软开关滑模观测器[J].电工技术学报，2015，30(2)：106-113. Lu Xiaoquan，Lin Heyun，Feng Yi，et al.Soft switching sliding mode observer for PMSM sensorless control[J].Transactions of China Electrotechnical Society，2015，30(2)：106-113.

[12]陈天翔，张辑，彭彦卿.基于转矩滑模观测器的抗负载扰动控制方法[J].电力系统保护与控制，2013，41(8)：114-118. Chen Tianxiang，Zhang Ji，Peng Yanqing.Anti-load distur-bance control method based on torque sliding mode obser-ver[J].Transactions of China Electrotechnical Society，2013，41(8)：114-118.

[13]Lidozzi A，Solero L，Crescimbini F，et al.SVM PMSM drive with low resolution Hall-Effect sensors[J].IEEE Transactions on Power Electronics，2007，22(1)：282-290.

[14]Mingshi H，Chinhao C，Hsinhung C，et al.An accurate torque control of permanent magnet brushless motor using low-resolution Hall-Effect sensors for light electric vehicle applications[C]//Energy Conversion Congress and Exposi-tion，Denver，2013：175-179.

[15]Capponi F G，De Donato G，Del Ferraro L，et al.AC brushless drive with low-resolution Hall-Effect sensors for surface-mounted PM machines[J].IEEE Transactions on Industry Applications，2006，42(2)：526-535.

[16]Tesch T R，Lorenz R D.Disturbance torque and motion state estimation with low-resolution position interfaces using heterodyning observers[J].IEEE Transactions on Industry Applications，2008，44(1)：124-134.

[17]Harke M C，De Donato G，Capponi F G，et al.Imple-mentation issues and performance evaluation of sinusoidal，surface mounted PM machine drives with Hall-Effect posi-tion sensors and a vector-tracking observer[J].IEEE Transactions on Industry Applications，2008，44(1)：161-173.

[18]Dalala Z M，Younghoon C，Jihsheng L.Enhanced vector tracking observer for rotor position estimation for PMSM drives with low resolution Hall-Effect position sensors[C]//Electric Machines and Drives Confer ence，Chicago，2013：484-491.

[19]Samyoung K，Chinchul C，Kyeongjin L，et al.An improved rotor position estimation with vector-track ing observer in PMSM drives with low-resolution Hall-Effect sensors[J].IEEE Transactions on Industrial Electronics，2011，58(9)：4078-4086.

Research on Detection and Control Optimized Approach for Permanent Magnet Servo Motors at Low Speed with Ordinary-Resolution Incremental Encoder

Wang Zhaodong Wen Xiaoqin You Linru Huang Zhaobin

(School of Automation Science and Engineering South China University of Technology Guangzhou 510640 China)

Aiming at the shortcomings of traditional control method for permanent magnet servo motors，an optimal speed detecting and controlling approach at low speed range is presented with ordinary-resolution incremental encoder in this paper.An extended M/T method is adopted for improving the speed of detection precision at ordinary-low speed range,and an improved T-method with closed-loop tracking feedback is employed for realizing high-precision speed detection at ultra-low speed range and an adaptive Proportion-Integration controller of reference speed is applied for obtaining a better speed control performance.Finally，sufficient experiments are implemented by the proposed approach on DSP controller and permanent magnet brush-less servo motor.Experimental results demonstrate that the dynamic performance at low speed is greatly enhanced and the adjustable speed range is extremely expanded.

Permanent magnet servo motor，incremental encoder，extended M/T method，adaptive PI controller，ultra-low speed

国家自然科学基金面上项目(61271210)和中央高校基本科研业务费专项资金项目(x2zd-D2154930)资助。

2015-05-25 改稿日期2015-10-16

TM351

汪兆栋 男，1981年生，博士研究生，讲师，研究方向为电机与运动控制、永磁同步电机控制。

E-mail：Wangzimochao@163.com(通信作者)

文小琴 女，1977年生，博士，讲师，研究方向为电力电子技术及其应用，数据处理。

E-mail：xqwen@scut.edu.cn