基于遗传算法的准零刚度隔振系统优化设计

蓝 双，杨晓翔

（福州大学 机械工程及自动化学院，福州 350000）

基于遗传算法的准零刚度隔振系统优化设计

蓝 双，杨晓翔

（福州大学 机械工程及自动化学院，福州 350000）

针对一种准零刚度隔振系统，建立其力学模型，求得准零刚度条件，分析系统在平衡位置的刚度特性。根据系统特点，提出将无量纲刚度＜1所对应的位移区间长度作为优化的目标函数。建立优化数学模型，结合遗传算法，提出一套准零刚度隔振系统的优化设计方法。建立隔振系统的Adams仿真模型，仿真结果表明优化后系统的隔振性能有很大的提升，验证优化方法的有效性和可靠性。为此类隔振系统的优化设计提供思路和参考。

振动与波；准零刚度；低频隔振；遗传算法；优化设计；Adams仿真

高精尖技术的不断发展，使得隔振技术尤其是低频隔振技术越来越受到人们的重视。由于线性隔振技术已经较为成熟，对于中高频振动的隔离已经可以很好地实现，而对于低频或者超低频振动的隔离，仍旧是一个研究的热点。因此越来越多的学者对低频或超低频隔振进行探索和研究。准零刚度隔振系统具有高静低动的特性，不仅具有较好的承载能力，也能保持很低的动刚度，在低频或超低频隔振中的效果十分明显。Carrella等提出经典的斜置弹簧并联垂直弹簧的隔振系统，对其进行静力学分析，并且研究了系统的力和位移传递特性[1-2]。Park等介绍了几种常见的正负刚度并联系统并进行理论分析，对它们的性能作了评价，提出改进方案[3]。Lan等设计一种由平面折叠弹簧组成的准零刚度系统，减小了系统的整体尺寸，并进行了理论分析和实验研究[4]。Sun等设计了一种在三个方向都有准零刚度特性的隔振系统，在空间隔振中具有很好的效果[5]。胡光军等将薄壁梁结构作为负刚度机构，建立静力学模型并进行试验研究[6]。刘兴天等采用欧拉梁作为负刚度元件，设计了一种正负刚度并联隔振器，并得出此类隔振器适用于隔离低频微小振动的结论[7]。

目前，国内绝大多数的文献都是针对准零刚度隔振系统的结构、理论和实验进行研究，鲜见针对系统的优化设计方法的报道。在国外，Carrella等对斜置弹簧式准零刚度系统的优化进行了研究[1]。大多数设计者都是凭借经验或试凑的方法确定隔振器的参数，并没有一套较系统的优化设计方法。

文中针对一种准零刚度隔振系统，建立力学模型，得到系统满足准零刚度特性所需的条件；根据系统的特点，建立隔振系统的优化数学模型，包括设计变量、目标函数和约束条件；利用遗传算法求解优化模型，得到系统的一组最优参数；建立系统优化前后的Adams虚拟样机，利用仿真结果证明优化的有效性和可靠性。

1 系统的力学模型

准零刚度隔振系统的结构简图如图1所示。其中，连杆的长度为a，载物台的长度为b；垂向弹簧的刚度为kv，原长为Lv0；拉伸弹簧的刚度为kh，原长为Lh0。假设一个垂直向下的力F作用于载物台，垂向弹簧向下压缩，拉伸弹簧处于拉伸状态，其长度设为Lh。当连杆处于水平时，系统处于平衡位置。

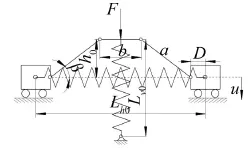
图1 准零刚度系统结构示意图

在垂直力F的作用下，假设载物台偏离平衡位置的位移为u，向下为正，则两者之间的关系为

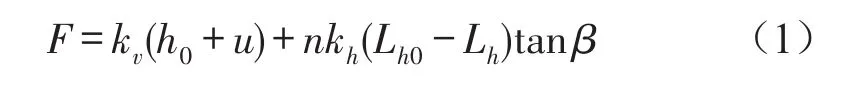
式中n为连杆的个数，文中n取为4，代入式（1）得

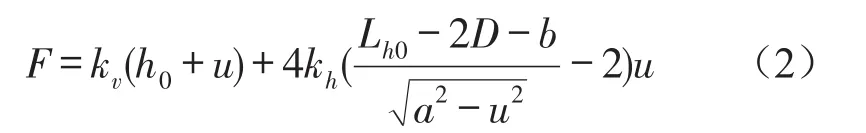
将式（2）等号两边同除以kvLh0，得到无量纲的力与位移关系式

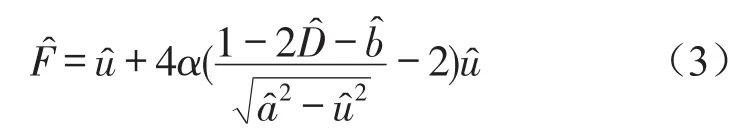
其中

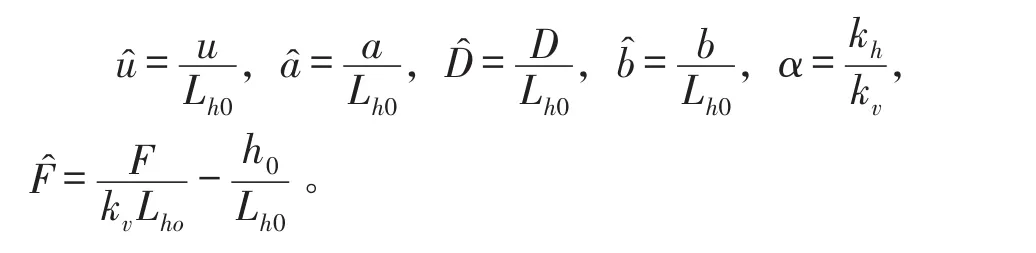
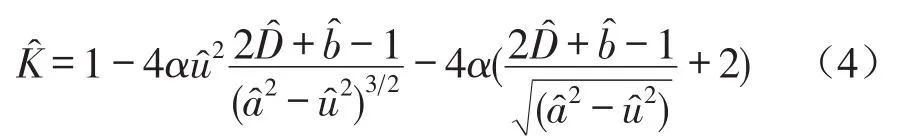
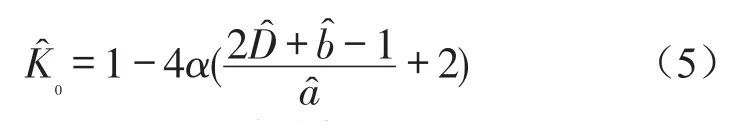
为了保证系统在平衡位置处的刚度为零，令式（5）等于零[1]，得到系统实现准零刚度特性所需要满足的条件

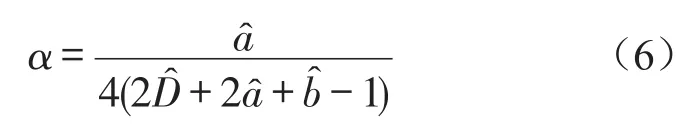
式（6）等价于

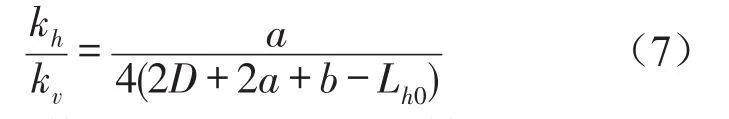
根据各零部件的空间布局要求、被隔振物体的重量和准零刚度条件，确定系统的参数如表1所示。

表1 隔振系统参数

将参数代入式（3）和式（4），得系统的力-位移特性曲线和刚度-位移特性曲线，如图2和图3所示。

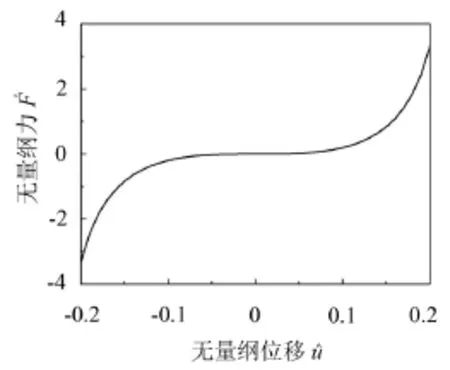
图2 力-位移特性曲线

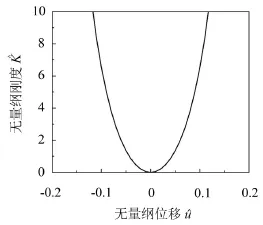
图3 刚度-位移特性曲线

从图中可以看出，系统在平衡位置的刚度为零。并且曲线在平衡位置附近有一段平缓区，称作准零刚度区间。该区间内系统刚度值很低，接近于零但大于零。隔振系统在该区间内具有准零刚度特性，不仅能够承载一定的质量，还具有较低的运动刚度，使系统具备低频或超低频隔振的能力[8]。

2 优化数学模型

2.1 目标函数的确定

与其他隔振系统的区别在于，准零刚度隔振系统在平衡位置附近有一个准零刚度区间，如图3所示。

当位移u保持这个区间内，系统的刚度很低，对应的曲线很平缓，隔振系统具有高静低动的特点，能够隔离低频或超低频振动。但是，如果当位移u超出准零刚度区间，即振动的幅值超过一定值时，系统的刚度就会发生大幅度的增加，刚度曲线变得陡峭，进而导致低频隔振效果迅速变差。所以，要提高准零刚度隔振系统的隔振性能，必须要尽量扩宽准零刚度的区间[1,9]。

根据式（4）可解得

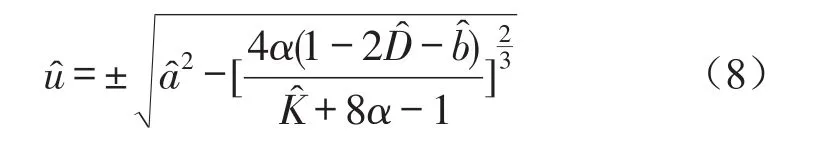
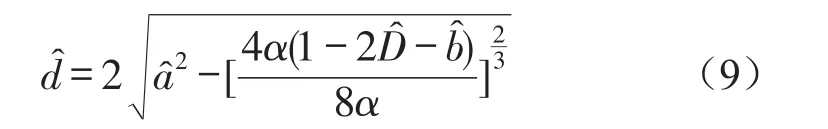
由于和d是等价的，所以目标函数式（9）等效于

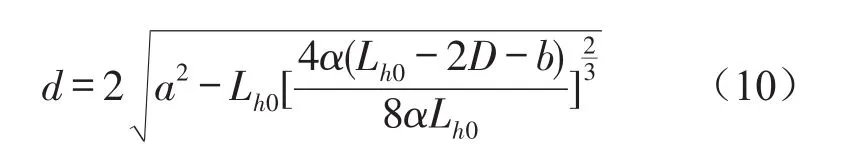
将式（10）等号右边的5个参数作为优化模型的优化变量，即a、b、D、Lh0、α。5个参数即可确定隔振系统。随机选择三组不同的参数，可得三个不同值的目标函数，其中如图4所示。

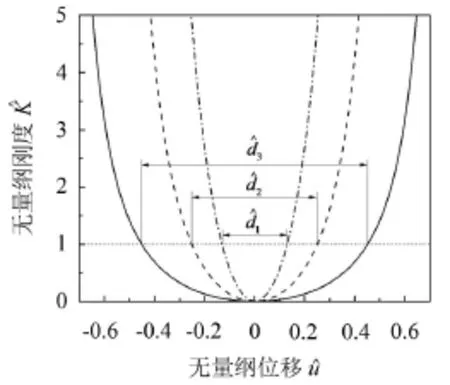
图4 不同的比较

2.2 约束条件的确定

只有当系统参数满足一定的条件时，系统才能表现出准零刚度特性。由式（6）可得如下等式约束

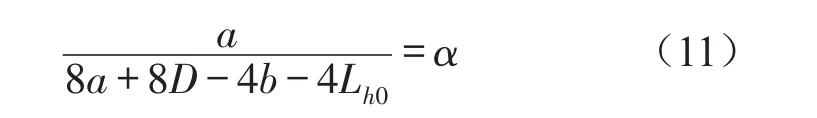
根据各个零部件的空间尺寸要求，建立系统各参数的取值范围如下。

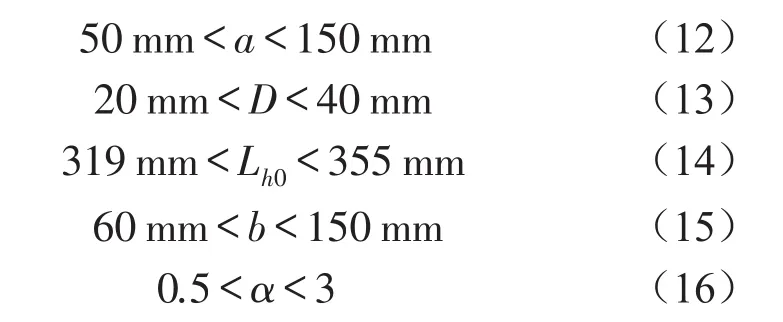
根据准零刚度隔振系统中各主要零部件的空间布局，以及总体尺寸的制约，确定如下约束条件

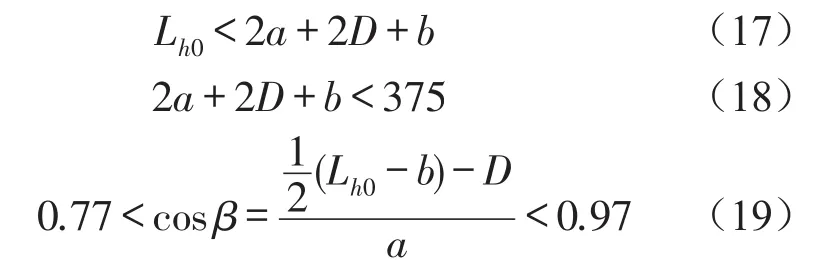
2.3 优化数学模型

以a、b、D、Lh0和α作为优化变量，无量纲刚度所对应的位移区间长度d作为目标函数。根据准零刚度条件、空间布置及尺寸要求等，建立模型的约束条件。其数学优化模型如下

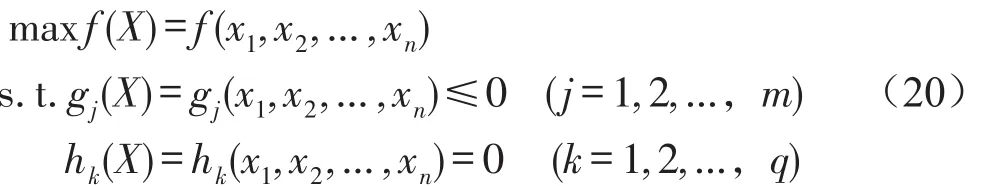
其中n=5，x1=a，x2=b，x3=D，x4=Lh0，x5=α，m=14，q=1。

3 遗传算法求解及结果比较

3.1 遗传算法求解

优化模型中的目标函数具有强非线性，且有5个优化变量，选择遗传算法较为合适。遗传算法是模拟地球上生物物种进化规律的一种随机优化方法。根据模式定理可知，品种越优良的后代越容易生存并且能够快速增长。由积木块假设可知，品种优良的个体相互交配后产生优良的后代，不断繁衍下去，使得求解不断向最优解逼近。

采用常见的二进制编码，初始种群的个体数为50，采用轮盘赌选择法，交叉概率为0.8，变异概率为0.1。图5为目标函数值随着遗传代数增加的变化情况。

图5 目标函数的变化过程

从图5可知，经过25代的遗传后，目标函数最优值趋近于60.6 mm，所对应的最优解为a=118 mm，b=66.4mm，D=20mm，Lh0=319mm，α=1.25。

3.2 优化前后结果对比

图6 优化前后系统的刚度—位移特性曲线

4 Adams仿真验证

根据优化前后的系统参数，建立各自的三维模型，导入到Adams中建立仿真模型，如图7所示。

图7 隔振系统的Adams仿真模型

在Adams模型中，在基座上添加不同频率的正弦位移激励，模拟地面激励。正弦位移激励为y=2sin(2πft)，激励频率f=1Hz～20 Hz。在被隔振物体上进行测量，采集物体在不同频率位移激励下的振动响应。对采集到的系统响应求均方根，作为系统响应的幅值。根据定义，隔振系统的响应幅值与激励幅值之比为位移传递率，可用来衡量隔振系统的性能。

Adams动力学仿真得到优化前后系统的位移传递率。为了凸显准零刚度系统优异的低频隔振性能，引入线性系统（被隔振物体和垂向弹簧组成的系统）的仿真传递率，三者的位移传递率如图8所示。

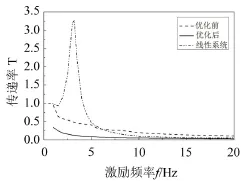
图8 位移传递率对比图

从图8可知，优化后的整体传递率小于优化前，尤其是在低频段，说明优化后系统的隔振范围被拓宽，隔振效率提高，性能有明显的提升。仿真结果证明了优化数学模型和优化方法的可靠性。并且，从图中可得准零刚度系统在低频段的隔振效果优于线性系统。但是，如果系统参数选择不当，可能导致中高频的隔振效果低于线性系统。

由图6可知，当系统偏离平衡位置时，刚度在准零刚度区间内会缓慢增加，但系统能保持低频或超低频隔振能力。当位移超出区间时，刚度会迅速增加，系统的隔振性能急剧变差。因此，激励的振幅也是影响系统隔振性能的重要因素之一。在Adams模型中，在基座上添加不同振幅的正弦位移激励，正弦位移激励为y=Asin(4πt)，激励幅值A=1mm～20 mm。同样在被隔振物体上进行测量，采集物体在激励下的响应。振幅变化对传递率的影响如图9所示。

由图9可知，系统在优化后的传递率比优化前下降了很多，性能得到改善。两者的传递率在振幅10 mm～20 mm区间会有所上升，但是优化后在整体上比优化前更平稳。当振幅为20 mm时，优化前系统的传递为0.72，而优化后系统的传递仅为0.37。说明优化后系统的准零刚度区间增大，能够降低幅值对传递率的影响，增强系统性能的稳定性。

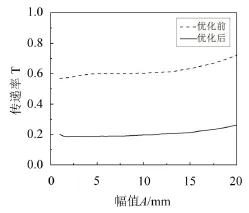
图9 激励振幅对传递率的影响

综上所述，优化后系统的低频隔振性能有很大的提升，不仅传递率有较大的下降，而且降低了振幅对传递性能的影响，增强了系统性能的稳定性，大大提升了隔振效率。

5 结语

建立准零刚度隔振系统的力学模型，得到准零刚度条件，分析系统在平衡位置的刚度特性。根据系统的刚度特性，将无量纲刚度＜1对应的位移区间长度作为目标函数，目标函数越大，准零刚度区间越大。建立优化数学模型，采用遗传算法对模型进行求解，得到一组最优参数，使目标函数的值增加了106%。ADAMS仿真结果表明，优化后系统的隔振性能有很大的提升，不仅传递率有较大的下降，而且降低了振幅对传递性能的影响，增强了系统性能的稳定性，从而验证了优化设计的有效性和可靠性。

[1]CARRELLA A,BRENNAN M J,WATERS T P.Static analysis of a passive vibration isolator with quasi-zerostiffness characteristic[J].JournalofSoundand Vibration,2007,301(3-5):678-689.

[2]CARRELLA A,BRENNAN M J,WATERS T P,et al. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic stiffness[J].International Journal of Mechanical Sciences,2012,55 (1):22-29.

[3]PARK S,LUU T.Techniques for optimizing parameters of negative stiffness[J].JournalofMechanical Engineering Science,2007,221(5):505-551.

[4]LAN C,YANG S,WU Y,Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads[J].Journal of Sound and Vibration, 2014,333(20):4843-4858.

[5]SUN XIU TING,JING XING JIAN.Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity[J].Mechanical Systems and Signal Processing,2015,62:149-163.

[6]胡光军，周生通，李鸿光.一种非线性隔振器的静力分析与实验研究[J].噪声与振动控制，2011，31(6)：69-71.

[7]刘兴天，孙靖雅，肖锋，等.准零刚度微振动隔振器的原理和性能研究[J].振动与冲击，2013(21)：69-73.

[8]HUANG X C,LIU X T,HUA H X,Effects of stiffness and load imperfection on the isolation performance of a highstatic-low-dynamic-stiffness non-linear isolator under base displacement excitation[J].International Journal of Non-LinearMechanics,2014.65:32-43.

[9]LE T D,AHN K K.Experimental investigation of a vibration isolation system using negative stiffness structure [J].International Journal of Mechanical Sciences,2013, 70(5):99-112.

(简讯)

2016全国声学设计与噪声振动控制工程技术高层论坛暨声学设计与噪声振动控制行业十周年联谊会在京举行

由北京国建信文化发展中心、中国声学设计与噪声振动控制网主办，中国环保产业协会噪声与振动控制委员会、中城科数智慧城市规划设计研究中心、中国城市科学研究会数字城市专业委员会轨道交通学组支持的2016全国声学设计高层论坛及十周年联谊会于2016年11月26-28日在北京江西大酒店召开，出席会议的有来自全国各地的代表130余人。

以北京国建信文化发展中心为主，从2006年以来十年间举办了15次全国性声学设计与噪声振动控制工程技术交流会，基本上每年举办1～2次，推动了这一行业的发展，为我国噪声与振动控制做出了突出的贡献。本次会议由廖龙英主任和戴佈和秘书长主持，首先回顾了十年来的发展历程，表彰了做出特别贡献的个人和单位，颁发了奖牌和奖杯，接着进行了学术交流。在大会上演讲的有陈祥福院士《绿色建筑与健康住宅》、张静建筑师《格局融合与智慧城市建设》、宋拥民博士《第11届中国艺术节开幕式主会场建声设计》、隋富生教授《声学材料和特性优化及应用》、张明发《上海申华公司22年发展历程回顾》、邵斌《城市轨道交通减振降噪技术热点探讨》等，对我国噪声控制和建筑声学的最新成果和发展方向进行了交流，会议出版了论文集，有关厂家展出了最新的声学材料和仪器设备，与会书法爱好者进行了技艺切磋和展示。与会者一致认为北京国建信文化发展中心提供的这一平台，为新老朋友交往、老中青结合、产学研联系创造了条件，会议开得生动、活泼、成功。

中船第九设计研究院工程有限公司吕玉恒（2016年11月28日报导）

Optimum Design for a Quasi-zero Stiffness Vibration Isolation System Based on GeneticAlgorithm

LAN Shuang,YANG Xiao-xiang
(College of Mechanical Engineering andAutomation,Fuzhou University,Fuzhou 350000,China)

Mechanical model for a quasi-zero stiffness vibration isolation system is established.The quasi-zero stiffness condition is obtained and the stiffness characteristic of the system in the equilibrium position is analyzed.According to the characteristic of the system,it is proposed that the length of the interval corresponding to the dimensionless stiffness is regarded as the objective function for optimization.Then,the optimal mathematical model is established.A method for＜1optimization of the quasi-zero stiffness vibration isolation system is presented.The simulation model is built by means of Adams.The results show that the performance of the optimized system is greatly improved.Finally,the reliability and validity of the optimization method is validated by the Adams simulation.This work can offer an idea and a reference for optimization of vibration isolation systems.

vibration and wave;quasi-zero stiffness;low frequency vibration isolation;genetic algorithm;optimum design;Adams simulation

TH113.1；O328

：A

：10.3969/j.issn.1006-1335.2016.06.034

1006-1355(2016)06-0173-05

2016-07-18

国家重大科学仪器设备开发专项（2011YQ090009）

蓝双（1990-），男，福建省龙岩市人，硕士生，主要研究方向为减振降噪。

杨晓翔，男，博士生导师。E-mail:yangxx@fzu.edu.cn