混合传递路径分析方法

杨立娟，罗新杰，苗慧慧，陈雪峰

（1.西安交通大学 机械工程学院，西安 710049；2.西安交通大学 青岛研究院，山东 青岛 266300）

混合传递路径分析方法

杨立娟1，罗新杰1，苗慧慧2，陈雪峰1

（1.西安交通大学 机械工程学院，西安 710049；2.西安交通大学 青岛研究院，山东 青岛 266300）

根据悬臂壳实验台结构建立有限元模型，并结合实验模态分析对其进行修正，建立高精度有限元模型。利用实验模态分析结果计算结构阻尼参数，确立混合传递路径分析（TPA）中频率响应函数(FRF)的有限元计算方法，并且与实验结果对比，验证其有效性和可行性。利用Tikhonov正则化方法进行载荷识别，对悬臂壳实验台进行混合TPA实验研究，获得不同频率下各路径对目标点振动的贡献量，并将各路径对目标点的振动贡献量进行矢量叠加，与实验测试值进行对比。结果表明，各路径贡献量叠加结果与实验测试值吻合较好，可确定该结构的主要振动传递路径，从而为结构优化奠定基础。

振动与波；混合传递路径分析；频率响应函数；有限元分析；Tikhonov正则化方法

对于复杂振动系统来说，寻找一种既能表征系统振动特性又较为简便快速的方法一直是振动研究中亟待解决的问题。近年来，基于系统频率响应函数（frequency response function，FRF）的传递路径分析（transfer path analysis，TPA）方法已成为复杂系统振动研究中的主要研究方法之一。TPA的研究主要涉及到FRF的获取方法与载荷识别算法的研究两个重要方面[1]。传统TPA中，采用基于模态分析的实验模态方法进行系统FRF的获取。模态分析方法是针对多自由度或连续体系统进行振动分析和识别动力学参数的比较有效的动态分析方法。但在TPA中为了获取所需要的系统FRF，要对分析对象进行拆卸测试[2]，而多数复杂系统在工程实际中无法进行拆卸测试，这就对实验模态方法的应用构成了障碍。随着有限元理论与计算机计算能力的发展，将有限元方法引入TPA分析中，产生了混合TPA分析[3-4]，应用有限元方法计算获取系统频响函数，为FRF的获得提供了新思路。载荷识别是个反问题，在实际工程中载荷识别误差往往会比较大，而Tikhonov正则化方法可以有效提高计算精度。

1 频响函数的获取

1.1 有限元模型的建立

利用高质量的有限元模型计算频响函数矩阵不单可以克服复杂系统无法测试的弱点，还可以避免实际测量误差、噪声等的影响。在有限元计算之前，需要得到准确的有限元模型，模型的准确性直接决定计算结果的准确性，这就涉及到边界条件、接触条件等模型修正问题。为了确定在实际工程中可以运用的有限元频率响应函数计算方法，文中进行了实验研究。实验对象是一个悬臂壳结构，如图1所示。

图1 实验平台

该壳结构长500 mm，厚5 mm，弧长为290 mm，直径为40 mm，材料为45钢，弹性模量为E=2.09×1011N/m2，泊松比μ=0.269，密度为7 890 kg/m3，结构阻尼未知。该结构通过螺栓与基座固定在一起。

首先完成有限元建模，由于该壳的厚度相对长度与宽度非常小，在有限元分析中将其弱化为平面问题，选用厚度5 mm的壳单元，有限元模型如图2所示。

图2 实验对象有限元模型

在完成有限元建模后，对实验对象进行锤击模态测试，见图3(a)，并通过对比有限元模态分析结果与实验测试结果，对有限元模型进行修正。实验测试采用LMS数据采集与模态测试设备，见图3（b），使用PCB公司的模态力锤对结构施加冲击激励，其型号为086C03，采用3个PCB公司333B32型加速度传感器采集响应信号。

图3 锤击模态实验

通过对比有限元模态分析结果与模态测试结果，修正有限元模型的边界条件，将壳体的边界条件设置为螺栓接触点约束时，有限元分析结果与模态测试结果相匹配，修正后的模型见图4。修正后的模型分析结果与模态测试结果对比见表1。

图4 修正后的有限元模型

由表1可看出，修正后的模型分析结果与模态测试结果最大误差为5.3%，结果匹配较好，这表明获得了高质量的有限元模型。

表1 模态结果对比

1.2 获取结构阻尼参数

在工程实际中，结构的阻尼是未知的，运用有限元方法计算系统FRF需要计算系统阻尼。文中使用比例阻尼计算结构阻尼，其阻尼矩阵为

式中[C]为阻尼矩阵；[M]为质量矩阵；[K]为刚度矩阵；α为质量阻尼系数；β为刚度阻尼系数。

有限元分析中需要的阻尼参数α与β通常是不能直接得到的，而是用振型阻尼比x计算出来的[5-6]。如果ωi是第i阶模态的固有角频率，ξi是第i阶振型阻尼比，根据振型正交条件，α和β满足下列关系

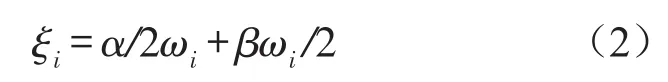
在给定固有频率范围ω1和ω2以及对应的阻尼比ξ1和ξ2后，解两个并列方程组便可求得α和β

式（3）与式（4）中固有角频率ω1和ω2，以及对应的ξ1和ξ2均可通过实验模态分析得到。模态实验的前两阶模态参数见表2。

表2 模态结果参数

将表2中参数代入式（3）与式（4）中，可计算得到该实验台的阻尼参数α=0.65，β=2.6110-5。

1.3 确立混合TPA的FRF获取方法

为得到系统的FRF，需要对系统的有限元模型进行谐响应计算。谐响应分析可以计算出结构在受迫振动时不同频率下的响应，当外载荷是单位激励时，即可得到频率响应函数[7-8]。

将计算得到的阻尼参数α和β赋于修正后的有限元模型中，在与锤击模态实验中对应激励点位置处分别施加单位正弦力，并进行谐响应分析，便可得到与锤击模态实验相同位置的频响函数。有限元分析结果和实验模态分析结果对比见图5。

由图5可看到，根据有限元方法计算得到的频响函数与实验模态测试得到的结果吻合很好，而且在某些范围内，有限元分析得到的曲线更加平滑，这充分说明了该方法在实际中的可行性。

图5 有限元分析与实验模态分析频响函数对比

2 利用Tikhonov正则化方法进行载荷识别

Tikhonov正则化方法可以提高载荷识别的精度。设测量响应为X，频率响应函数为H，X和H都存在误差，为控制及度量误差，设整体绝对误差为e，满足

式中F为系统所受外载荷。

为使误差e尽量小，Tikhonov引入罚函数

在式（6）中，当J对F的1阶导数为零时，误差e存在最小值，则可得到F。

式中I为单位矩阵；λ为正则化参数。

实验对象采用前面的悬臂壳，实验系统见图6。

图6 实验系统

利用激振器施加两个160 Hz正弦激振力，并利用两个安装在激振器与壳结构之间的阻抗头采集激振力。在壳上布置7个加速度传感器，其中，载荷识别时使用其中6个，这6个作为系统振动响应的采集点，称为计算参考点。在载荷识别中为保证计算有解，响应测点数目必须大于激励力数目。在本次试验中，有两个利用激振器施加的激励力，响应点至少需要两个。为保证载荷识别的准确性及传感器采集数据正确性所需的冗余传感器，综合考虑选择6个点作为载荷识别的参考点。载荷识别的结果见图7。

3 混合TPA的实验研究

利用有限元模型获取FRF，采用Tikhonov正则化方法进行载荷识别，对悬臂壳结构进行混合TPA研究。实验系统仍采用图6所示悬臂壳结构，激振器作为振源和两条路径，激振器与壳接触的位置即为两个路径点。在壳上布置7个加速度传感器，其中6个作为系统响应的采集点，一个作为传递路径分析的目标点（图6中方框所示），采集目标响应信号。对悬臂壳进行混合TPA分析，路径点与参考点之间、路径点与目标点之间的频响函数矩阵由之前修正好的有限元模型（如图4所示）通过计算获取；采用Tikhonov正则化方法进行载荷识别，结果见图7；之后由式（8）计算得到由各路径传递到目标点处的振动信号

图7 载荷识别结果

式中Ti(ω)为路径点i对目标点T振动的贡献量；Hi(ω)为路径点i到目标点的频响函数；Fi(ω)为路径点i上所受到的路径载荷。

根据目标点处实测振动响应信号、由载荷辨识得到的载荷与采用有限元分析获得的FRF进行计算得到的目标点响应结果的对比见图8。

图8 混合TPA分析结果

目标点处实测振动信号与TPA计算得到的两路径响应结果叠加值对比如图9。

图9 目标点测试响应与两路径叠加结果

由图8可看到，在90 Hz附近，即壳的1阶固有频率处，两路径传递到目标点的振动均很大；在100 Hz～150 Hz范围内，路径2传递到目标点的振动明显高于路径1；在200 Hz～300 Hz范围内，路径1传递到目标点的振动明显高于路径2；在400 Hz～450 Hz范围内，路径2传递到目标点的振动明显高于路径1。根据有限元模态计算得到悬臂壳的1至5阶固有频率为89.51 Hz、155.19 Hz、349.57 Hz、381.24 Hz、455.72 Hz，由此可以看出，1阶至2阶、4阶至5阶固有频率近似范围内，路径2贡献量大，2阶至3阶近似频率范围内路径1贡献量大。这跟结构的振动振型有关，在特定频率范围内，结构的某些部位振动大，某些部位振动小。

从图9中可以看出，目标点处振动响应与两条路径叠加结果吻合较好，可以得出该目标点响应为这两条路径传递而来，进而确定了目标点处振动的传递路径。

4 结语

建立了悬臂梁壳结构的有限元模型，确定了混合传递路径分析中频响函数的有限元计算方法，并通过模态实验验证了该方法的有效性。针对悬臂壳实验台进行了混合传递路径分析实验，通过分析得到不同频率下各传递路径对目标点振动的贡献量，确定目标点处的主要振动传递路径，找出振动源及产生原因。根据混合TPA分析结果，可以对结构进行优化调正，避免目标点处在所关注特定频段内出现振动问题。有限元分析在传递路径分析中的应用，解决了复杂结构频响函数难以获取的问题，有利传递路径分析的发展。

[1]郭荣，裘剡，房怀庆等.频域传递路径分析方法(TPA)的研究进展[J].振动与冲击，2013，32(13)：49-55.

[2]唐贵基，陈卓群.混合传递路径分析（TPA）方法的准确性验证[J].噪声与振动控制，2015，35(2)：184-187.

[3]PLUNT J.Finding and fixing vehicle NVH problems with transfer path analysis[J].Sound and Vibration,2005,39 (11):12-17.

[4]KIM S J,OG K G,KIM S G,et al.Estimation to interior noise by using hybrid transfer path analysis[J].Noise Control Engineering Journal,2008,56(4):256-268.

[5]吴成军.工程振动与控制[M].西安：西安交通大学出版社，2008.

[6]陈建群.基于信号分析的结构模态参数提取方法[D].西安：长安大学，2009.

[7]张洪才.ANSYS 14.0理论解析与工程应用实例[M].北京：机械工业出版社，2012.

[8]RONASI H,JOHANSSON H,LARSSON F.Load identification for a rolling disc: finite element discretization and virtual calibration[J].Computational Mechanics,2012,49(2):137-147.

The Method for Mixed Transfer PathAnalysis

YANG Li-juan1,LUO Xin-jie1,MIAO Hui-hui2,CHEN Xue-feng1
(1.School of Mechanical Engineering,Xi’an Jiaotong University,Xi’an 710049,China; 2.Qingdao R&D Institute,Xi’an Jiaotong University,Qingdao 266300,Shangdong China)

The finite element model of the structure of a cantilever-shell test bench is established and modified through the modal test to obtain a high-precision model.The structural damping parameters are calculated using the results of the modal test.Then,the method of acquiring frequency response functions(FRF)based on the finite element model is established,and the effectiveness and the feasibility of this method are verified by the modal test.By means of load identification using Tikhonov regularization method,the transfer path analysis(TPA)of the cantilever-shell is finished by the mixed transfer path analysis method,and the contribution of each transfer path to the vibration of the target points is obtained for different frequencies.Then the contributions of all transfer path are superimposed,and the result is compared with the measured signals.The results show that the superimposed results are in good agreement with the measured signals and the principal transfer paths of vibration of the structure can be determined with this method.This study has provided the basis for the structural optimization.

vibration and wave;mixed TPA;FRF;finite element analysis;Tikhonov regularization method

O241.82；O329

：A

：10.3969/j.issn.1006-1335.2016.06.003

1006-1355(2016)06-0012-04+20

2015-12-29

国家杰出青年科学基金资助项目（51225501）

杨立娟（1989-），女，山东省泰安市人，工程师，主要致力于结构有限元分析、信号测试与分析等相关研究工作。E-mail:yang_lijuan@mail.xjtu.edu.cn