非局部理论的裂纹纳米谐振梁振动特性
2016-12-27郭旭晓张文明
郭旭晓,周 含,张文明
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
非局部理论的裂纹纳米谐振梁振动特性
郭旭晓,周 含,张文明
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
以两端固支纳米谐振梁为研究对象,考虑非局部效应、非线性轴向拉伸应力以及裂纹建立其物理模型并推导出运动控制方程。将裂纹等效为连接两段纳米梁的扭转弹簧,研究非局部效应、裂纹参数对系统自由振动固有频率以及振动模态的影响。采用非线性静电力和非线性轴向拉伸应力模型,用多尺度的数值方法研究系统主谐波共振响应的非线性刚度硬化现象与非局部效应系数以及裂纹各参数的关系。数值结果表明,非局部效应系数越大,系统固有频率越小,主共振非线性强度越大。对于两端固支谐振梁系统,裂纹位置对系统固有频率以及主共振非线性强度的影响存在着三个分界点,分别是纳米梁中点以及距离两端四分之一的两个点。研究结果可在微纳米器件的设计、性能改进及健康检测中得到应用。
振动与波;纳米梁;裂纹;非局部效应;非线性响应
梁状结构是微纳米机电系统中典型的基本组成部分,并且极大地影响了该类微纳米器件的性能,因此对微/纳米梁的动力学特性研究具有重大的实际意义[1-3]。研究纳米梁机械特性的方法主要有三种:实验研究、分子动力学模拟、连续介质力学理论。由于纳米梁的尺度范围较小,所以进行核对实验较为困难,而分子动力学模拟需要大量的计算量,对于大尺度系统难以实施,所以连续介质力学理论是研究纳米梁机械特性和振动特性的重要方法。Daquesnes等人[4]分别用分子动力学和连续体模型研究了碳纳米管在不同边界条件下的吸合特性和自然频率,他们发现两种方法得到的结果相吻合。
对于尺寸量级与分子距离相当的微纳米机构,众多实验以及仿真结果都显示了非局部效应对其机械特性产生显著影响,经典的连续介质理论已无法准确预测其力学行为,纳米尺度结构受到的影响比微米尺度结构更加明显[5]。由Eringen在1983年提出的非局部弹性理论具有简单的本构关系[6],特别是Peddieson等人提出的形式,能够简单而有效地研究非局部效应对纳米结构力学特性的影响,解决了在纳米梁、板、壳等结构中的众多问题[7]。
近年来,微纳米梁的线性和非线性动力学特性研究进展较快。傅衣铭[8]等采用数值方法分析了考虑尺度效应的纳米梁线性自由振动特性以及非线性幅频响应特性。基于非局部弹性理论,Mesut等采用变分法研究了多种边界条件下纳米梁由于轴向拉伸力引起的的非线性特征[9]。刘灿昌等从梁的轴向非线性伸长出发对纳米梁进行受力分析,研究了纳米梁非线性特性产生的物理机制,分析了非局部效应对纳米梁振动特性的影响[10]。
然而以上研究主要以无缺陷的完整结构为研究目标,如果结构出现缺陷,其对结构的力学特性造成的影响不容忽视。理论研究以及工程应用中,裂纹一直是固体材料结构中存在的重要问题。裂纹的存在引起了结构柔度变化,减小了器件振动的固有频率,对结构特性造成了不容忽视的影响。Sáez等人采用扭转弹簧等效纳米梁裂纹,他们发现该方法获得的结果与用有限元得到的结果一致[11]。刘文光等人将复数阻尼理论应用于裂纹梁的结构振动研究,使其与疲劳裂纹扩展寿命估算同步进行,提出一种含裂纹结构的振动疲劳分析思路[12]。Motallebi等人以静电驱动谐振梁为研究对象,探讨了开始裂纹参数对谐振梁吸合效应的影响[13]。刘素娟等人基于Euler-Bernoulli理论,提出了非线性静电力和压膜阻尼效应下裂纹微悬臂梁的动力学模型与分析方法,研究了耦合作用下裂纹微悬臂梁结构的振动特性[14]。
基于非局部弹性理论,研究裂纹纳米梁的振动特性,建立考虑非局部效应、非线性轴向力以及裂纹的纳米谐振梁的运动控制方程,研究非局部效应以及裂纹参数对纳米梁固有频率的影响。采用多尺度的数值分析方法,探讨了非局部效应以及裂纹各参数对主共振幅频响应曲线的影响,对裂纹纳米梁的非线性振动特性进行研究。
1 振动模型与控制方程
图1所示为两端固支静电驱动单裂纹纳米谐振梁模型,仅考虑横向振动,假定梁的各截面的中心主惯性轴在同一个平面oxy内,外载荷也作用在该平面内,梁在该平面内作横向振动,梁的两端固定运动受阻,引起中性面拉伸。对于细长梁,剪切变形以及截面绕中性轴转动惯量的影响可忽略不计。图中裂纹距左固定端长为Xc,纳米梁长度、厚度、宽度分别为L、h、b,密度为ρ、d为中性轴距底面距离,截面对中性轴的二次矩是I,且I=bh3/12。左端固支点为零点,x和w(x,t)分别代表沿着纳米梁长度方向的坐标以及在t时刻的横向振动位移。

图1 两端固支静电驱动单裂纹纳米谐振梁模型[13]
取梁的微元dx进行受力分析,如图2所示。在微元左侧,梁受到的垂直剪力为Q,弯矩为M,Na为非线性轴向拉伸应力,且Nr为残余应力,文中记为常量[15]。右侧为相应的受力变化,为作用于梁上的非线性分布力[16],ε0为介电常数,A=bh,为横截面面积。由力和力矩的平衡条件可得到


图2 纳梁微元受力分析图
根据非局部弹性理论可知应力-应变关系为[5]

其中E为杨氏模量,σx和εx为经典理论中的应力与应变,参数μ=(e0a)2表征纳米结构小尺度效应的长度量纲系数。
由非局部本构关系可得到如下非局部效应下的轴向拉伸应力以及力矩与变形之间的关系

将式(4)代入式(1)和式(2),考虑系统的阻尼并等效为弹性阻尼c,可得图1所示的静电驱动纳米梁横向振动控制方程为

两端固支梁的边界条件为

为了便于定性分析,对式(5)、式(6)引入无量纲变量

进行无量纲化处理,并将标号*去掉可得无量纲化振动控制方程以及边界条件为

2 振动分析
2.1 自由振动分析
对式(8)引入变量分离表达式w(x,t)=Y(x)ejωt,则纳米梁的静态自由振动方程为

其中ω为固有频率,λ4=ω2为频率参数。式(10)的数值解的模态函数为

如图1所示,裂纹距左固定端的长度为Xc,这时图3为裂纹梁等效模型。将裂纹等效为无质量扭转弹簧,记△θ和△u为微裂纹引起的扭转角以及相应的水平位移[5],则二者可表示为

图3 裂纹梁等效模型

其中kMM、kMN、kNM、kNN为柔性系数。在仅考虑横向振动的情况下,纵向振动为零(u(x,t)=0),并且系数kMN、kNM、kNN一般被认为是很小的值。因此,裂纹处的斜度增量可表示为如下无量纲形式

其中无量纲长度为Lc=Xc/L,裂纹因子表示裂纹开裂程度。
此时,基于式(8),裂纹梁两段的静态自由振动方程为表示为

且Ai、Bi、Ci、Di( )i=1,2为各段相应常数,由边界条件以及裂纹处的相容性条件,即式(9)、式(17)联立而得的8×8阶矩阵方程求解得出,相应的第n阶固有频率参数λn也可同时求解。
2.2 主共振分析
图1中谐振梁的静电驱动载荷由直流电Vp以及交流电vac组成,驱动频率为ωe,且Vp≫vac,则

方程的右边表达式可表示为

为研究纳米梁的非线性特性,希望得到梁振动的幅频特性[17]。为此,仿照通常做法,取横向振动的变量分离形式并将其与式(19)代入式(8)可得由达芬方程描述的系统动力学方程
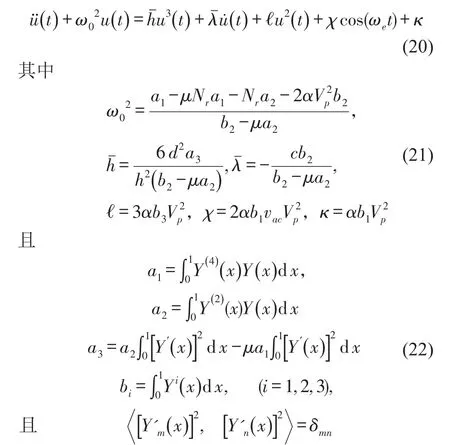
上述系统的振动为弱非线性时变系统的参激振动,应用多尺度法求一次近似解,首先引入两个越来越慢的时间尺度Tn=εnt(n=0,1),其中ε为小参数,并假设u()
t可以表示为如下形式

研究系统ωe≈ω0时的主共振,引入频率调谐因子σ,使得ωe=ω0+εσ。记χ=εχ,κ=εκ,式(20)可改写成

将式(23)代入式(24),并令两端ε0和ε1的系数分别相等,可得

方程式(25)的解为
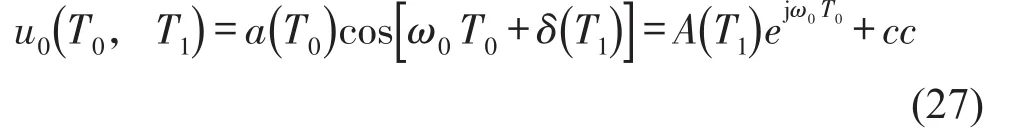
其中cc表示前项共轭。
将式(27)代入方程式(26),消除永年项,并分离实虚部,可得如下自治微分方程

其中φ=σT1-δ。为确定对应稳态运动的定常解振幅和相位,令D1a=D1φ=0,并消去ε,对于可得到ωe的实系数二次代数方程

将激励频率无量纲化,取Ω=ωe/ω0,可得

其中主共振峰值大小满足如下等式

出现最大峰值时的激励力频率为

3 结果分析与讨论
以两端固支裂纹纳米谐振梁为仿真实例,谐振梁的相关物理参数为L=250 nm,b=50 nm,
3.1 裂纹梁固有频率分析
通过数值计算方法计算方程式(15)得到考虑非局部效应以及裂纹参数的纳米梁前4阶固有频率。图4显示了裂纹位置处于纳米梁中点处即Lc=0.5时,不同非局部效应系数μ对应的前4阶固有频率随着裂纹因子K的变化趋势。
由图4可见,裂纹开裂程度越大,且非局部效应系数越大,系统的固有频率越小,即纳米梁的材料刚度降低。当K增大到一定值时,固有频率的变化将趋于固定值而不再变化。由图中还可以看出,第2、4阶固有频率不随裂纹因子的变化而变化(见图4(b)、(d)),这是由于两端固支梁振动模态的对称性,裂纹所在处恰好为2阶、4阶振型节点处,从而对纳米梁2阶、4阶的振动频率没有影响[18]。同理,当裂纹位置Lc=0.25时,纳米梁的第4阶固有频率不随裂纹开裂程度发生变化。因此,对于两端固支梁可以总结出,当裂纹位置与固有频率对应的阶数n满足条件nLc=N时,裂纹梁的第n阶固有频率不随裂纹开裂程度的变化而变化。图5显示了当裂纹开裂程度不变,即K为常量时,纳米梁前4阶固有频率随着裂纹位置Lc的变化趋势。由于纳米谐振梁的对称性,其固有频率的变化趋势都将关于中点对称。
从图5(a)可知,裂纹位置为Lc=0.25、Lc=0.75是另外两个分界点。当裂纹在此位置左边时,裂纹越接近该位置,纳米梁1阶频率越大;而当裂纹在此位置右边时,当裂纹越接近中点处,1阶固有频率越小。裂纹越接近纳米梁两端根部,固有频率越小。从图5(b)可知,2阶频率变化趋势的分界点更多。频率对应的阶数越大,其随裂纹位置的变化趋势越多变。另外,与图4结果相补充,当裂纹在纳米梁任意位置处,非局部效应系数越大,固有频率越小。

图4 非局部效应裂纹纳米梁前4阶固有频率随裂纹因子K的变化趋势(Lc=0.5)

图5 非局部效应裂纹纳米梁前2阶固有频率随裂纹位置变化趋势(K=1)
3.2 主共振特性分析
由式(30)可得到两端固支裂纹纳米谐振梁的1阶主谐波共振的幅频响应(AFR)曲线,AFR曲线的弯曲程度显示了纳米梁振动的非线性强度。由图6、图7可知,非局部效应系数以及裂纹参数对纳米梁振动的非线性特性都有显著影响,两端固支梁存在分叉和跳跃等非线性现象,幅频关系存在着多值性,并且曲线都向右弯曲,具有刚度硬化效应。当激励频率小于谐振频率时,谐振梁幅值较小,当频率增加到某一频率时,位移突然增大,而后又陡然下降,随着激励频率持续增加,谐振梁的振动位移又越来越小,几乎不发生谐振,与已有的实验结果相符合[19]。
从式(20)中可知,系统存在固有几何非线性特性,并且立方刚度项的大小受非局部效应系数以及裂纹参数的影响。从图6中可以看出,随着非局部效应系数的增大,系统谐振频率逐渐变大,系统刚度渐硬趋势更明显。
从图7中可以看出,裂纹位置为Lc=0.25是裂纹位置对谐振梁幅频响应影响趋势的一个分界点,当裂纹在此位置左边时,裂纹越接近该位置,系统刚度硬化趋势越明显;而当裂纹在此位置右边时,当裂纹距离该位置越远,系统刚度硬化趋势减弱。对于两端固支谐振梁,裂纹位置为Lc=0.25是系统刚度硬化最强的位置,而Lc=0.5则是系统刚度硬化最弱的位置,此现象与图5(a)所显示的规律相对应。

图6 非局部效应对裂纹纳米梁主共振非线性的影响(Lc=0.25)

图7 裂纹位置对裂纹纳米梁主共振非线性的影响(μ=0.2)
4 结语
以静电驱动裂纹纳米谐振梁为研究对象,采用无质量扭转弹簧模型模拟裂纹,考虑非局部效应以及非线性轴向拉伸应力的影响,建立系统动力学模型,对系统自由振动的固有频率以及振动模态、主谐波共振的幅频响应进行研究。研究发现非局部效应系数对裂纹纳米谐振梁固有频率影响很大,裂纹处于梁上任意位置,固有频率都随着非局部效应系数的增大而减小。忽略一些特殊情况(nLc=N),考虑非局部效应时,高阶频率受到的影响远远大于低阶频率。裂纹开裂程度越大,固有频率越小,但该影响随着开裂程度的增大而减缓。裂纹位置对固有频率的影响依情况而定。非局部效应以及裂纹参数对系统的主谐波共振的幅频响应都有影响,并且与其对系统固有频率的影响趋势相对应。
[1]BUNCH J S,VAN DER ZANDE A M,VERBRIDGE S S, et al.Electromechanical resonators from graphene sheets [J].Science,2007,315(5811):490-493.
[2]CHASTEJ,EICHLER A,MOSER J,etal.A nanomechanical mass sensor with yoctogram resolution [J].Nature Nanotechnology,2012,7(5):301-304.
[3]GAVARTIN E,VERLOT P,KIPPENBERG T J.A hybrid on-chip optomechanical transducer for ultrasensitive force measurements[J].Nature Nanotechnology,2012,7(8): 509-514.
[4]DEQUESNES M,ZHI T,ALURU N R.Static and dynamic analysis of carbon nanotube-based switches[J].Journal of Engineering Materials and Technology, 2004,126(3):230-237.
[5]LOYA J,LÓPEZ-PUENTE J,ZAERA R,et al.Free transverse vibrations of cracked nanobeams using a nonlocal elasticity model[J].Journal of Applied Physics, 2009,105(4).
[6]ERINGEN A C.On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics,1983,54(9):4703-4710.
[7]PEDDIESONJ,BUCHANANGR,MCNITTR. Application of nonlocal continuum models to nanotechnology[J].International Journal of Engineering Science,2003,41(3-5):305-312.
[8]FU Y,ZHANG J,JIANG Y.Influences of the surface energies on the nonlinear static and dynamic behaviors of nanobeams[J].Physica E:Low-Dimensional Systems and Nanostructures,2010,42(9):2268-2273.
[9]ŞIMŞEK,M.Large amplitude free vibration of nanobeams with various boundary conditions based on the nonlocal elasticity theory[J].Composites Part B:Engineering, 2014,56:621-628.
[10]刘灿昌,裘进浩,季宏丽,等.考虑非局部效应的纳米梁非线性振动[J].振动与冲击,2013,32(4):158-162.
[11]FERNÁNDEZ-SÁEZ J,NAVARRO C.Fundamental frequency of cracked beams in bending vibrations:an analytical approach[J].Journal of Sound and Vibration, 2002,256(1):17-31.
[12]刘文光,陈国平.含裂纹悬臂梁的振动与疲劳耦合分析[J].振动与冲击,2011,30(5):140-144.
[13]MOTALLEBI A,FATHALILOU M,REZAZADEH G. Effect of the open crack on the pull-in instability of an electrostatically actuated micro-beam[J].Acta Mechanica Solida Sinica,2012,25(6):627-637.
[14]刘素娟,齐书浩,张文明.静电驱动裂纹微悬臂梁结构振动特性分析[J].振动与冲击,2013,32(17):41-45.
[15]FATHALILOU M,MOTALLEBI A,REZAZADEH G,et al.Mechanical behavior of an electrostatically-actuated microbeam under mechanical shock[J].Journal of Solid Mechanics,2009,1:45-57.
[16]张文明,孟光,周健斌.微机电系统压膜阻尼特性分析[J].振动与冲击,2006,25(4):41-45.
[17]刘延柱,陈立群.非线性振动[M].北京:高等敎育出版社,2001.
[18]HASHEMINEJAD B S M,GHESHLAGHI B,MIRZAEI Y,et al.Free transverse vibrations of cracked nanobeams with surface effects[J].Thin Solid Films,2011,519(8): 2477-2482.
[19]朱年勇,于虹,黄庆安.纳机械谐振器的非线性特性分析[J].电子器件,2005,28(1):35-37.
Vibration Characteristics of a Cracked Resonant Nano-Beam Considering the Nonlocal Effect
GUO Xu-xiao,ZHOU Han,ZHANG Wen-ming
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University, Shanghai 200240,China)
Characteristics of free transverse vibration and forced vibration of a cracked resonant nano-beam with both ends fixed are studied.The nonlocal effect,nonlinear axial stretching force and the crack effect are considered.The cracked nano-beam is modeled as two segments connected by a massless rotational spring located in the crack section.Dynamic equations of the nano-beam are derived and its nonlinear response is investigated by using the multiple scales method.The influence of the nonlocal effect and the crack position on the vibration nonlinearity is discussed.The numerical results show that enlarging the nonlocal effect coefficient can decrease the values of the natural frequencies and strengthen the nonlinearity of the resonant vibration.The effects of the crack parameters on the vibration characteristics are complicated. This study may be of interest for the design,performance improvement and health monitoring of nano-devices.
vibration and wave;nano-beam;crack;nonlocal effect;nonlinear response
O346.1
:A
:10.3969/j.issn.1006-1335.2016.06.001
1006-1355(2016)06-0001-06
2016-07-27
国家优秀青年科学基金项目(11322215);国家高层次人才特殊支持计划项目(青年拔尖人才);教育部霍英东青年教师基金项目(141050)
郭旭晓(1990-),男,山东省潍坊市人,硕士生,主要研究方向为微机电系统动力学。
张文明(1978-),男,博士生导师。E-mail:wenmingz@sjtu.edu.cn
