步长自适应的前向后向匹配追踪算法
2016-12-26张松江张传林
张松江 周 密 张传林
(暨南大学信息科学技术学院 广东 广州 510000)
步长自适应的前向后向匹配追踪算法
张松江 周 密 张传林
(暨南大学信息科学技术学院 广东 广州 510000)
稀疏度自适应的匹配追踪算法(SAMP)是基于压缩感知理论的信号重建经典算法。针对稀疏度未知的信号重建,提出步长自适应的前向后向匹配追踪(AFBMP)算法,AFBMP算法在稀疏度自适应匹配追踪算法的框架下,前向搜索过程中采用对数型自适应变化的步长选择匹配原子,然后通过后向策略修正前向阶段造成的错误,删除支撑集中的部分错误原子,最终实现信号的精确逼近。实验表明AFBMP算法比SAMP算法能够更加高效地重建稀疏度未知的信号。
压缩感知 重构 前向后向 稀疏度自适应 匹配追踪算法
0 引 言
随着科学技术的飞速发展,在信号的采样和处理过程中,利用信号的带宽来表示信号已不能满足现实的需要,因为随着信号携带的信息量逐渐增加,采样速度和处理速度就会变得越来越慢,同时这些数据的存储问题也是不容忽视的。虽然人们采用一种压缩的方式来表示信号,但是这种方式会导致大量的信息资源被抛弃,所以采用带宽来表示信号的信息是不合理的。而信号的稀疏性是近几年信号处理领域的新宠,它可以更加本质地表示信号,因此基于信号的稀疏性提出的压缩感知理论得到了广泛的认可。
压缩感知理论(CS)[1,2]作为一种全新的采样理论,利用随机采样获取信号的离散样本,然后通过非线性重建算法对信号进行重建。该理论指出:如果信号在某个变换域上是稀疏的或者认为是可以压缩的,那就可以通过一个新的观测矩阵将高维的信号映射到一个低维空间中,这样就可以将问题转化为最优化问题,进而重构出原始信号。该理论通过稀疏性以及等距约束准则来完成高速率的采样,又包含了大量的重要信息。压缩感知理论因为可以同时完成数据的采集和压缩,大大节约了时间和资源,所以得到了广泛的应用。
虽然压缩感知理论可以大大降低采样和计算的成本,但是如何设计出一种快速的鲁棒的重建算法是该理论的核心问题。随着对CS理论研究的不断深入,为了通过低维数据来实现对原始信号的重构,近年来越来越多的重构算法被提出。目前贪婪迭代算法是学者们研究最多的算法,这种算法重构精度高、计算量小并且易于实现。比如Mallat等人采用正交策略提出了正交匹配追踪算法(OMP)[4,5]、Needell又在正交匹配追踪算法放入基础上加入正则化思想,提出正则化正交匹配追踪算法(ROMP)[6]、Tropp根据随机测量矩阵思提出了压缩采样匹配追踪算法(CoSaMP)[7]、Dai借鉴回溯序贯编码理论,提出了子空间追踪算法(SP)[8]以及Donoho等人考虑稀疏度未知的情况,打破传统局限,提出了一种稀疏度自适应的匹配追踪算法(SAMP)[9,10]。贪婪迭代算法因其重建速度快和精度高而得到广泛应用,然而大部分贪婪算法都是通过已知稀疏度来控制算法重建的迭代次数,而在实际问题中,稀疏度不一定是已知的,并且当稀疏度固定时也可能会对重构精度造成影响。
SAMP算法突破了传统的匹配算法要以稀疏度已知为前提的限制,解决了在稀疏度未知的条件下的重建问题。SAMP算法的重建速度主要取决于固定步长的选择,虽然在重构精度上有了一定的提高,但是依然不能得到满意的效果。另外根据该算法的迭代机制,每次迭代过程中都会增加支撑集中的原子个数,这样就会有越来越多的原子被加入到支撑集中,而又无法删除支撑集中部分错误原子,所以该算法有一定的局限性。为了解决这一问题,有学者提出了MSAMP算法[11],该算法在SAMP算法的框架下通过原子匹配估计稀疏度,然后利用阶段步长来实现对原始信号的估计,但这种算法在同一阶段的步长依然是一个固定值,因此重构精度很大程度上依赖于每个阶段步长的选择。而LSAMP算法[12]则是在不同的阶段采用了对数型变化的步长,该算法在采样率较低时重构效果依然很好。但是这些算法本质上都属于前向贪婪算法,前向算法最大的缺点就是不能修改前一步迭代造成的错误,原子一旦被选入支撑集便无法删除。例如图1所示,假设特征向量x是由观测矩阵中的向量α1、α2构成,然而观测矩阵中另外一个向量α3比其他两个向量更接近特征向量x,这样当采用像OMP、SAMP这类前向贪婪算法时首先会选择α3,之后才会选择α1、α2,并且这类算法还不能删除α3,这样的结果并不是我们想要的。事实上,只有在观测矩阵中的向量不相关时前向贪婪算法才比较适用。
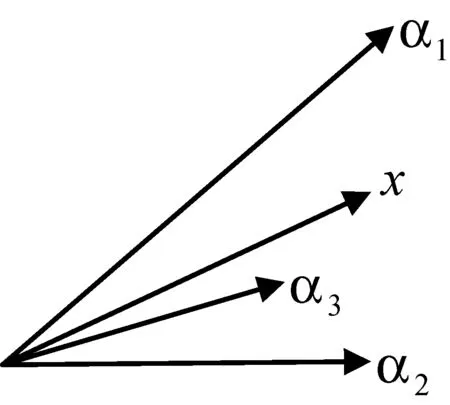
图1 特征向量图示
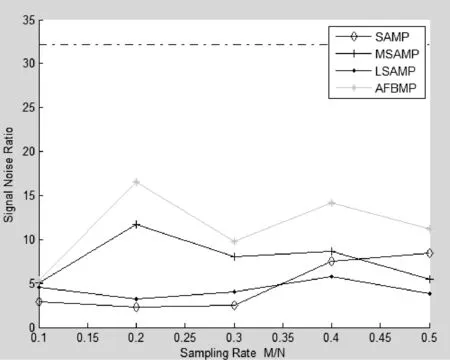
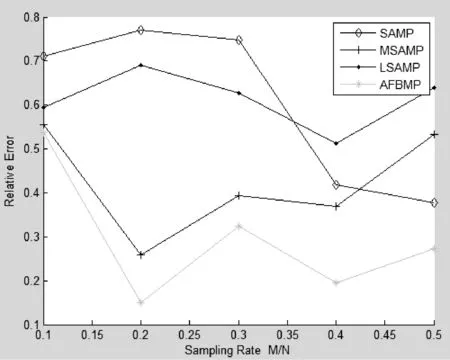
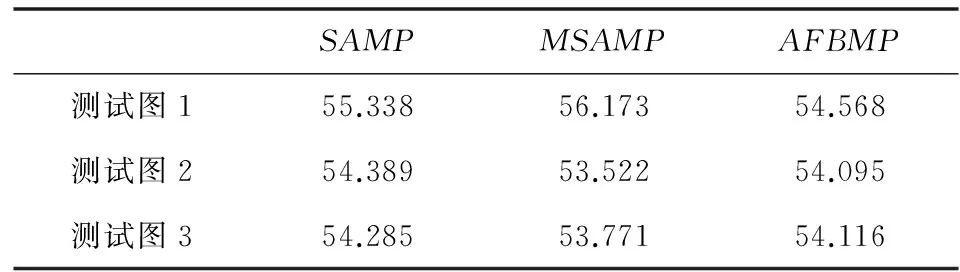
考虑到前向贪婪算法的缺点,很容易想到利用后向贪婪算法来进行改善。后向贪婪算法首先选择全部原子,然后逐一删除使重建误差最小的原子。这种算法虽然不会陷入局部最优问题,但是其计算代价非常高,因为一般情况下观测矩阵中M< 目前压缩感知理论在很多方面得到了应用,比如:吴延海提出了基于改进SP算法的压缩感知图像重构[13],廖斌提出了一种基于压缩感知的盲数字水印算法[14],李秀霞提出了基于压缩感知的合成孔径雷达图像目标识别[15]等。越来越多的学者们将压缩感知利用到人脸识别、医学CT图像重建、语音识别、卫星遥感图像融合、无线传感器网络、探地雷达成像中。因此对压缩感知理论的进一步研究就变得十分有意义。 假设x为长度为N的原始稀疏信号,即x的稀疏度为K,K< 通常采用求解以下最优化问题来从测量信号y中重建出信号x: min‖x‖0s.t. y=Φx (1) 对于式(1)求最优解问题是NP难题[16-18],而最小化l2范数问题又不能保证解的稀疏性。但是Candes等人指出,如果x足够稀疏,Φ满足约束等距条件RIP(Restricted Isometry Property)[19]时: (2) 其中, δK∈(0,1)表示K稀疏度下的约束等距常数,此时就可以将问题转化为求解l1范数最小化: min‖x‖1s.t. y=Φx (3) 通过利用匹配追踪算法就可以进行对式(3)的近似求解。OMP算法、ROMP算法等都是在给定稀疏度的基础上进行的重构,然而在实际应用中,信号的稀疏度K往往是未知的,这在一定程度上给信号的重构带来了挑战,于是Thong T.Do等人为了解决这一问题,提出了稀疏度自适应的匹配追踪算法,将信号重构问题转化为分阶段处理的过程,打破了传统的稀疏度已知的限制。之后更多学者专注于对SAMP算法的改进,比如变步长的MSAMP算法和对数型变步长的LSAMP算法。这些算法很好地解决了步长固定问题,重构效果也得到了很大的改善。 SAMP算法实现了在稀疏度未知的情况下对信号的重构。该算法首先选取步长step,然后计算余量r和观测矩阵Φi的内积,其中Φi表示观测矩阵的每一列,根据内积值,选取size个最大的相关系数,将这些系数所对应的原子加入到索引集中。接着合并上一阶段产生的支撑集得到候选集,再进行一次余量与候选集的内积,同样选取size个相关系数最大的原子作为支撑集F。此时更新余量r,如果当前余量小于迭代前的余量,则继续迭代,否则进入下一阶段,根据步长更新支撑集容量size=size×step,重复上述步骤,直到余量r小于某个阈值停止迭代。 具体算法如下: (1) 余量r=y,支撑集长度size=step,阶段stage=1,支撑集F=∅; (2) 计算余量r和Φi内积的绝对值,从中选取size个最大值对应的索引值得到索引集S; (3) 将索引集与上一阶段的支撑集进行合并,得到候选集C=F∪S,再计算候选集与余量的内积,并提取size个最大值,将其相对应的原子加入到支撑集Fnew; (5) 若‖rnew‖2≥‖r‖2,则进行下一迭代阶段,stage=stage+1,利用初始步长更新支撑集容量size=stage×step,返回步骤(2)继续迭代;否则更新支撑集和余量F=Fnew,r=rnew,此时迭代次数k=k+1,返回步骤(2)继续迭代。 从上述算法中可以看到各个迭代阶段步长step的取值是一个常数,步长的选择关系到支撑集的容量,因此该算法的重构精度与该步长选择有很大的关系。但是该算法的最大缺点就是不能后向删除部分错误原子,在原子的原子过程中很有可能会产生一些错误的、冗余的原子,如果没有办法进行二次修正,不仅会影响算法的时间,也会影响算法的精度。因此本文结合以上算法的优点,针对不能后向删除错误原子提出了利用对数型自适应变化步长的前向后向算法来实现信号的重建。 SAMP算法虽然突破了在传统匹配算法中对稀疏度的限制,但是通过相关实验表明,为了加快重构速度,初始步长step取较大值时,算法只需要很少的迭代次数,但是算法的效率就会很低。如果想保证算法的重构精度,step取很小的值时,迭代次数就会大大增加。另外传统的算法在选择原子过程中支撑集的容量是不断增加的,但是又无法删除那些错误的或者冗余的原子。因此选取合适的步长和利用后向策略来对算法进行修正是提高算法性能的关键。根据文献[12]结合对数函数的性质,在SAMP算法的框架下,提出了步长自适应变化的前向后向匹配算法。该算法首先进行前向选择匹配原子,然后进行向后剔除部分错误原子[20],在确保重建精度的情况下,弥补了前向贪婪算法自身的缺点。接下来将从两个方面对新算法进行具体描述:步长选择和算法描述。 3.1 步长选择 根据相邻迭代阶段重建信号差的变化规律,设置两个阈值ε1、ε2(ε1>ε2),当‖xt-xt-1‖>ε1时,选取一个较大的步长,实现快速逼近;当ε2<‖xt-xt-1‖<ε1时,选取较小的步长,以实现逐渐逼近,此时步长变为上阶段步长的一半;当‖xt-xt-1‖<ε2时说明相邻阶段的能量差变化趋于平稳,则停止迭代。 设步长step为: step(s)=alog2s+b (4) (5) 而当采取缓慢逼近策略时就选取前一阶段步长的一半,即: (6) 这里的步长均向上取为正整数,c≥1的正整数,M、N分别表示观测信号和待估信号的长度。 3.2 算法描述 (1) 初始化稀疏度:余量r=y,支撑集F,支撑集长度size=step,阶段stage=1,迭代次数t=1,索引值集合S=∅,候选集C=∅; (2) 计算相关系数,从中提取size个最大值对应的索引值放入到集合S中; (3) 合并索引集S与支撑集F,得到候选集C=F∪S,再计算候选集中索引值对应的原子与余量的内积,并提取size个最大值对应的索引值得到新的支撑集F; (4) 由最小二乘得到xt=argmin‖y-ΦFxt-1‖2,更新余量rt=y-Φtxt-1; (5) 如果‖xt-xt-1‖>ε1则转步骤(6),否则转步骤(8); (6) 如果‖rt‖≥‖rt-1‖则转入步骤(7),否则转入步骤(9); (7) 进入下一阶段,stage=stage+1,利用式(5)求出新步长step,扩大支撑集大小size=size+step,t=t+1,返回步骤(2); (8) 如果‖xt-xt-1‖<ε2则停止迭代,否则转入步骤(10); (9) 更新支撑集和余量返回步骤(2)继续迭代; (10) 进入小步长阶段,stage=stage+1,利用式(6)求出新步长step,扩大支撑集大小size=size+step,t=t+1,返回步骤(2); (12) j=argmini∈Fq(F/i); (13) d-=q(F/j)-q(F); (14) d+=ε3; (15) 如果d- 实验一 为了验证本文算法的有效性,通过MATLAB处理平台对该算法进行了验证。实验一中采用长度为N=256的一维高斯稀疏信号,观测矩阵为部分快速傅里叶变换矩阵(FFT)。阈值设置为ε1=e-6,迭代停止条件阈值ε2=e-12,ε3=e-14。在实验一中比较了SAMP算法、MSAMP算法、LSAMP算法和AFBMP算法在不同采样率下的重构效果。实验中除本文算法以外其他算法的参数均按照原参考文献中设置。实验表明该算法的重构效果很好,相对误差非常小,能够很好地对原始信号进行重建,在理论上说明了新算法的有效性。 图2是SAMP、MSAMP算法、LSAMP算法与AFBMP算法在不同采样率下重构信号信噪比的比较。其中横坐标表示采样率,纵坐标为信噪比,实验结果显示,该算法在前向阶段通过采用对数型变化的步长选取匹配原子,后向阶段删除错误原子,使得该算法的性能得到了明显的提升,AFBMP算法提高了对原始信号的重构精度。 图2 不同采样率下重构信号的信噪比 图3比较了四种算法在不同采样率下的重构相对误差。实验发现,SAMP算法在不同采样率下的重构误差相对很高,而MSAMP算法和LSAMP算法是对原来算法的改进在一定程度上均降低了重构的相对误差,而AFBMP算法结合了前面几种算法的优点,使得重构相对误差变得更低。我们发现,在相同采样率下,AFBMP算法比其他三种算法的相对误差低很多,因此该算法充分保证了对稀疏信号的重构精度,同时也证明了该算法的有效性。 图3 不同采样率下几种算法的相对误差 实验二 为了更为充分地说明新算法在实际问题中的应用,本文实验二对大小为256×256的图像进行实验。阈值设置为ε1=e-6,迭代停止条件阈值ε2=e-12,ε3=e-14。将本文算法和经典SAMP算法、MSAMP算法对三组测试图像进行比较。图4表明,改进的SAMP算法重构效果均好于经典SAMP算法,而AFBMP算法的重构效果也明显好于其他算法,同时也证实了本文算法的实用价值。 图4 二维图像重建效果 表1是这三组测试图进行重构的运行时间,从上节的实验可知不同的采样率下对算法性能的影响很大,因此采样率为0.5的情况下重构时间如表1所示。 表1 不同图像不同算法的重构时间 通过表1可以看出在相同的采样率下,对于不同的图像,各种算法的重构时间也有所不同,而AFBMP算法的重构时间略低于传统的SAMP算法,进一步说明了本文算法在运行时间上有一定的优势。 本文深入研究了压缩感知理论的经典算法,在稀疏度未知的情况下结合SAMP算法,提出了一种对数型自适应步长的前向后向匹配算法。SAMP算法在迭代过程中固定步长可能会导致过估计或者欠估计的问题,并且迭代结束之后不能删除某些冗余原子和错误原子。针对这两个问题,在SAMP算法框架基础上,前向迭代过程中采用改进的对数型可变化的步长选取匹配原子,而向后阶段逐一测试支撑集中的每一个原子,删除前向阶段所产生的错误原子,通过设置双阈值来控制步长选择和停止准则,分段逐步实现对稀疏度的逼近,最终实现信号的精确重构。实验结果表明,新算法可以较好地实现未知稀疏度信号的重建,且重建性能明显优于SAMP算法。 [1] Candes E J,Wakin M B.An introduction to compressive sampling[J].IEEE Signal Proc Mag,2008,25(2):21-30. [2] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theroy,2006,52(4):1289-1306. [3] Chen S B,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SiamJ.Sci.comput,2001,20(1):129-159. [4] Mallat S,Zhang Z.Matching Pursuit with time-frequency dictionaries[J].IEEE Trans.Sig.Proc,1993,41(12):3397-3415. [5] Tropp J,Gilbert A.Signal recovery form random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information theory,2007,53(12):4655-4666. [6] Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].IEEEJournal of Selected Topics in SignalProcessing,2010,4(2):310-316. [7] Needell D,Tropp J A.Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321. [8] Dai W,Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on information theory,2009,55(5):2230-2249. [9] 郭永红,杨毅彬.一种稀疏自适应的正交互补匹配追踪算法[J].计算机工程与应用,2013,49(7):144-146. [10] Donoho D L,Tsaig Y,Drori I,et al.Sparse solution of underdetermined linear equations by stage wise orthogonal matching pursuit[J].IEEE Transaction on Information Theroy,2012,58(2):1094-1121. [11] 朱延年,赵拥军,孙兵.一种改进的稀疏度自适应匹配追踪算法[J].信号处理,2012,28(1):80-86. [12] 毕学霞,尚振宏.一种基于变步长的稀疏度自适应匹配追踪算法[J].系统仿真学报,2014,26(9):2116-2125. [13] 吴延海,闫迪.基于改进SP算法的压缩感知图像重构[J].计算机应用与软件,2013,30(7):200-203,216. [14] 廖斌,任美玲,徐俊刚.一种基于压缩感知的盲数字水印算法[J].计算机应用与软件,2014,31(2):307-311. [15] 季秀霞,卞晓晓.基于压缩感知的合成孔径雷达图像目标识别[J].计算机应用与软件,2013,30(12):120-123. [16] 李然,干宗良,朱秀昌.基于最佳线性估计的快速压缩感知图像重建算法[J].电子与信息学报,2012,34(12):3006-3012. [17] Baraniukr R.Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-126. [18] Candes E,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomeplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509. [19] Do T T,Gan L,Nguyen N,et al.Sparisity adaptive matching pursuit algorithm for practical compressed sensing[J].IEEE Asilomar Conference on Signals,Systems and Computers,2008,10(7):581-587. [20] Wei Tang,Zhenwei Shi.Regularized simultaneouss forward-backward greedy algorithm for sparse unmixing of hyperspectral data[J].IEEE Transactions on geoscience and remote sensing,2014,52(9):5271-5288. ADAPTIVE STEPSIZE FORWARD-BACKWARD MATCHING PURSUIT ALGORITHM Zhang Songjiang Zhou Mi Zhang Chuanlin (School of Information and Science Technology,Jinan University,Guangzhou 510000,Guangdong,China) Sparsity adaptive matching pursuit algorithm (SAMP) is a classical algorithm of signal reconstruction based on compressed sensing theory. Aiming at reconstructing signals with unknown sparsity, we presented an adaptive stepsize forward-backward matching pursuit algorithm (AFBMP). In the framework of SAMP, AFBMP selects matching atoms in its forward search process by using logarithmic adaptive changing steps, and then amends the mistakes caused in forward stage by backward strategy to delete part of the false atoms in support set, and finally realises accurate signal approaching. Experiments show that the AFBMP algorithm can reconstruct the signals with unknown sparsity more efficiently than SAMP algorithm. Compressed sensing Reconstruction Forward-backward Sparsity adaptive Matching pursuit algorithm 2015-09-15。张松江,硕士,主研领域:图像处理。周密,硕士。张传林,教授。 TP391.9 A 10.3969/j.issn.1000-386x.2016.11.0571 压缩感知理论以及重构算法
2 SAMP算法及其改进
3 步长自适应的前向后向匹配追踪算法
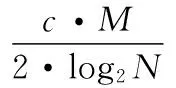
4 实验与分析


5 结 语
