基于径向基神经网络的新型协同过滤推荐算法

叶兰平 刘 锋 朱二周

(安徽大学计算机科学与技术学院 安徽 合肥 230601)



基于径向基神经网络的新型协同过滤推荐算法

叶兰平 刘 锋 朱二周*

(安徽大学计算机科学与技术学院 安徽 合肥 230601)

针对传统协同过滤推荐算法对目标用户的评分预测过于依赖邻近用户，而忽略目标用户自身评分特性的问题，提出一种改进的基于径向基RBF(Radial Basis Function)神经网络的预测方法。该方法首先使用RBF神经网络对邻近用户的项目评分数据进行模型训练，得到基于该用户的网络评分模型；然后结合目标用户自身的评分进行计算，得到一个基于该模型的评分；最后结合所有邻近用户的模型评分预测出目标用户对目标项目的最终评分。改进后的算法既借鉴了用户之间的相似性，也考虑了目标用户自身的评分特性。实验结果表明，改进后的协同过滤推荐算法可以获得比传统算法更好的推荐效果。

协同过滤 评分偏差 RBF神经网络 用户评分模型

0 引 言

当前，协同过滤推荐算法主要研究用户群对产品群的评分预测[1]。通过计算分析所有用户对项目的评分找到与目标用户相似的邻近用户集合，将该集合中所有邻近用户对目标项目的评分与目标用户之间的相似度相结合，用于预测目标用户对该目标项目的评分[2-4]。但是在这种计算方式中，目标用户的评分结果太过依赖邻近用户的评分，而忽略了其自身的评分特性。与此同时，协同过滤推荐算法中的用户评分数据稀疏以及新用户加入时冷启动等问题，都会对用户之间相似度的计算产生比较大的影响[5]。

当评分数据比较稀疏或有新用户加入时，计算所得用户之间相似度的可靠性往往比较低，此时实质上不太相似的两个用户看起来会比较相似。这样的邻近用户对目标项目的评分易产生比目标用户真实的评分过高或者过低的偶然性，而这种偶然性会造成目标用户的目标项目评分预测产生较大误差。

为了降低这种误差，需要把目标用户与邻近用户之间的相似度和目标用户自身的评分特性更好地结合起来。据此，本文提出一种基于RBF径向基神经网络的对传统协同过滤推荐算法进行改进的方法。首先，使用RBF神经网络对目标用户的每个邻近用户的评分数据进行建模；然后，把目标用户自身的评分数据输入到建立好的网络模型中，经过计算可以得到一个基于该网络模型的数据评分；最后，结合所有网络模型的数据评分进行计算，就可以得到最终的预测结果。实验表明，改进后的算法在评分数据比较稀疏和计算所用的邻近用户数量大的情况下，可以提高目标用户对目标项目评分的准确度。

1 相关工作

1.1 传统的协同过滤推荐算法描述

协同过滤推荐算法的基本假设是如果两个用户之间的兴趣相类似，那么其中一个用户很有可能会喜欢另外一个用户感兴趣的东西[6,7]。基于这一点找出与目标用户兴趣相近的邻近用户集合，然后借助该集合中邻近用户对目标项目的喜好来预测目标用户对该项目的喜好程度。

(1) 用户—项目评分的表示

假设在用户评分数据库中共包括s个用户和t个项目，用U={u1,u2,…,us}表示这s个用户集合，I={I1,I2,…,It}表示t个项目集合，则用户评分数据可用一个二维矩阵表示，如表1所示。

表1 用户—项目评分表P(s×t)

表1中Pi,j表示的是用户ui对项目Ij的评分，通过该评分可以判断用户ui对项目Ij的喜好程度。

(2) 用户相似性度量的方法

用户之间相似度的计算通常转化为用户评分向量之间相似度的计算。本文采用向量空间相似性中的余弦相似性度量方法。标准的余弦相似性通过向量间的余弦夹角来度量[8]：

(1)

其中Pi,k、Pj,k分别表示用户ui和uj对项目Ik的评分。

为了更精确计算向量间的相似度，文献[5]采用了修正余弦相似性度量方法。该方法选取了用户ui和uj的评分交集(Iui∩Iuj)，并定义为I′。此时，向量间相似度的计算如下：

(2)

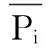
(3) 协同过滤推荐结果的产生

计算得到用户之间相似度之后，找出与目标用户ui相似度最高的且对目标项目Ik都有过评分的N(N≥1)个邻近用户，定义T(Ui)为这N个近邻用户的集合，所以有|T(Ui)|=N。通过式(3)就可以计算目标用户对目标项目的评分：

(3)

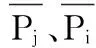
1.2 RBF径向基神经网络简介

RBF径向基神经网络是一种高效的前馈式神经网络，可以处理系统内难以解析的规律性。同时，RBF神经网络也是一种局部逼近网络，故其具有很高的自学习效率[9,10]。现今，该网络主要应用于解决函数曲线逼近和模式分类等问题。

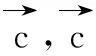
(4)

其中，bj为一个正的标量，表示高斯基函数的宽度；m是隐含层节点数量。网络最后的输出由如下加权函数实现：

(5)

其中ωj是输出层的权值。

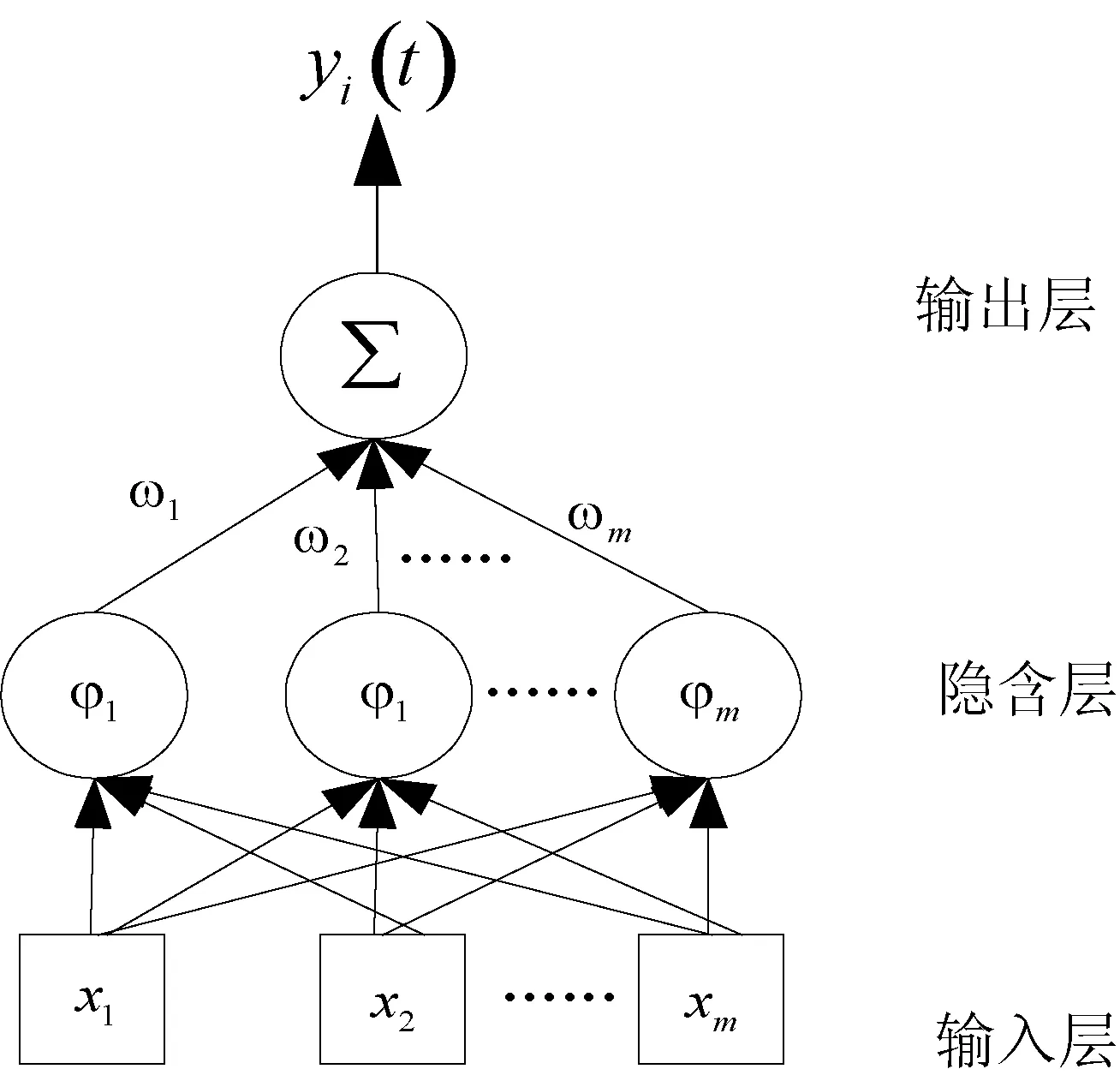
图1 RBF径向基神经网络结构图

RBF径向基神经网络结构相比其他网络，具有更好的泛化能力，网络结构简单，可以避免不必要的冗长计算。同时，研究表明，该网络能在一个紧凑集和任意精度下，逼近任何非线性函数[11]。基于以上分析，本文选择使用RBF径向基神经网络对传统的协同过滤算法进行改进。

2 基于RBF神经网络的协同过滤推荐算法

2.1 传统协同过滤推荐算法的缺陷

为了说明本文提出的评分偶然性，建立如表2所示的一个“用户—项目”评分表。该表中的数据取自豆瓣电影中的部分评分，为空的表项表示用户在该项目上没有评分。

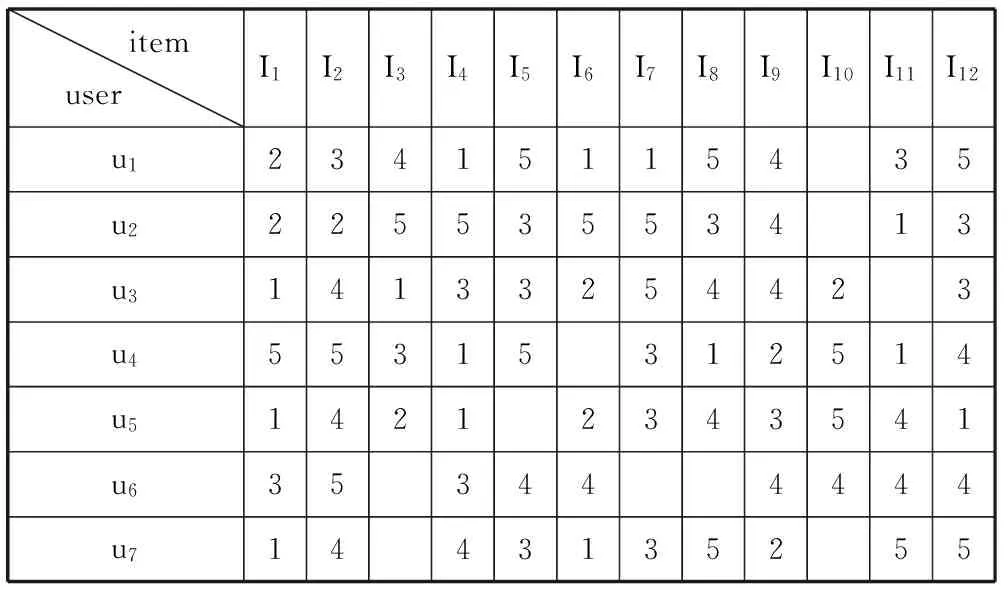
表2 用户—项目评分表P(7×12)

这里I1-I11为测试项目，I12作为目标项目，这样计算用户之间相似度时只需使用用户u1-u7对项目I1-I11的评分。

计算得出用户之间的相似度如表3所示。

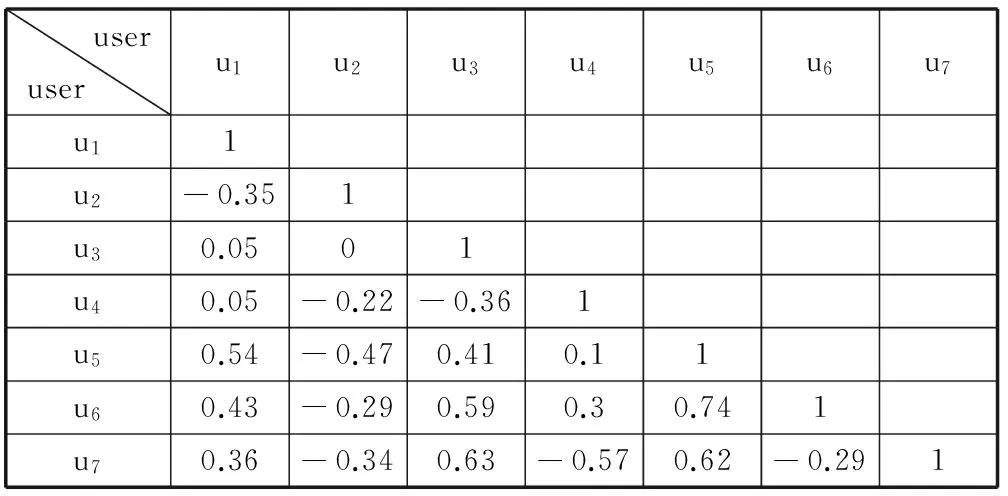
表3 基于表2的用户相似度表

从表3中选出相似度最大的4对邻近用户组，分别为[u6,u3]、 [ u6,u5]、[u7,u3]和[u7,u5] (按行优先)。定义DIx(ui,uj)为用户ui与uj在项目Ix上的评分差的绝对值，这个值越大则说明用户之间评分的偏差就越大。

从表2中看出，在对项目I1～I11的评分上，这4对邻近用户组的DIx(ui,uj)基本都在[0, 2]之间。但在对目标项目I12的评分上，DI12(u7,u5)=4和DI12(u6,u5)=3的评分偏差就比较大了，而同样是邻近用户组的[u6,u3]和[u7,u3]的评分偏差就比较正常。对目标项目I12的评分中所出现的上述情况就是邻近用户对目标项目的评分过高或者过低的偶然性，而在传统的协同过滤推荐算法中却忽略了这一点。

2.2 改进型协同过滤推荐算法提出的依据

从表2中用户u5与u7的评分来看，u7的评分相比u5高一些，故P7,12=5符合其评分特性；而u5的评分要低一些，故P5,12=1也同样符合u5的评分习惯。由于DI12(u7,u5)=4，如果P7,12=5借助来预测用户u5对I12的评分则会产生较大偏差。同理，邻近用户组[u6,u3]之间也存在这个问题。如果把目标用户自身的评分特性和与邻近用户之间的相似性结合起来，计算所得的评分会更接近目标用户自身的真实评分，就可以达到缩小用户之间评分偏差的目的。这种结合刚好可以使用RBF神经网络来完成。

文献[12]提出“如果两个邻近用户的兴趣爱好相似，那么他们对整体项目的评分曲线应该是互相接近的”。据此我们分别作出表2中4对邻近用户组在他们共同评分项目上的评分曲线，如图2-图5所示。

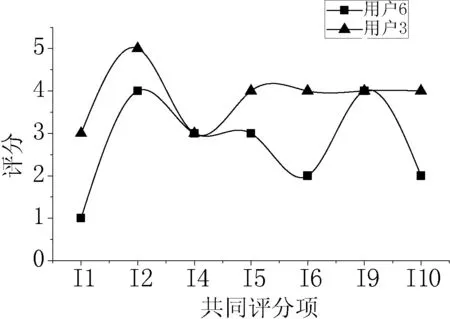
图2 用户u6、u3评分曲线图

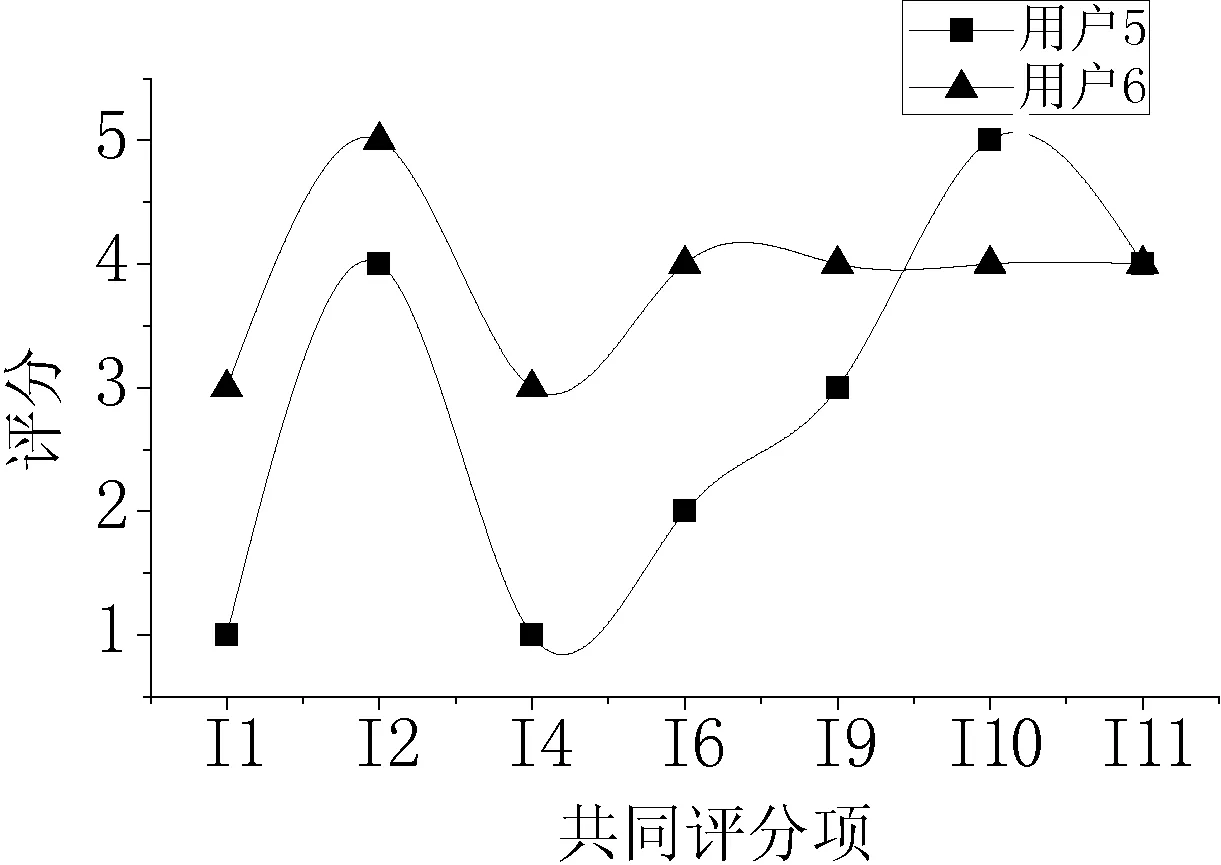
图3 用户u6、u5评分曲线图

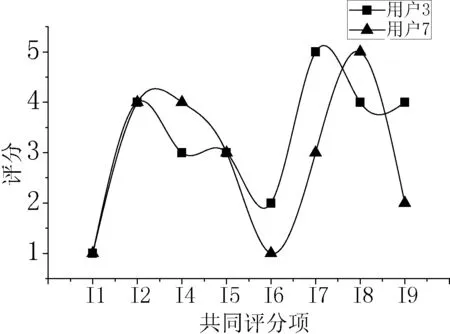
图4 用户u7、u3评分曲线图

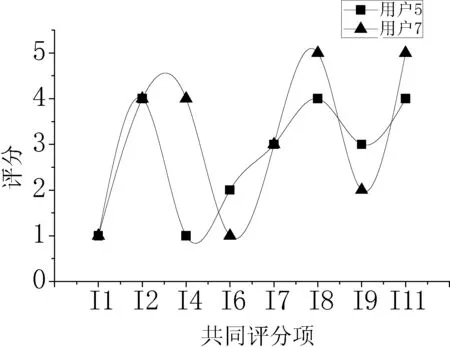
图5 用户u5、u7评分曲线图

从图2-图5的4张曲线图看出，除个别点外，两个相邻用户的评分曲线在整体上的升降趋势是一致的，说明两条曲线之间是相互逼近的。由于RBF神经网络对非线性函数具有很好的逼近能力，则可以使用该网络对邻近用户的评分来建立基于该用户的网络评分模型。把目标用户的项目评分输入到训练好的模型中，经过计算可以得到一个参考目标用户自身评分数据的初步评分结果。并在最后结合所有的初步评分结果对目标项目进行预测。这种改进方式的优点在于既考虑了用户之间的相似性，也考虑了目标用户自身的评分特性。

2.3 算法设计与实现

基于RBF径向基神经网络改进的协同过滤推荐算法主要的工作在于如何通过该网络训练得到基于邻近用户评分数据的网络模型。这里定义目标用户为ui，目标项目为Ik，目标用户的邻近用户集合为T(ui)，Px,k表示用户ux对项目Ik的评分，Iux为用户ux评分向量。Q(Iui,ux)为用户ui、uj之间共同评分过的项目集合，即Q(Iui,ux)=Iui∩Iux，则用户ux中属于共同评分的项目为Q(Iui,ux)∩Iux，记作R(Iux)。

算法步骤如下：

(1) 计算目标用户的邻近用户集合T(ui)。

(2) 建立基于用户ux评分的RBF神经网络评分模型。首先，找出Iux中属于共同评分的项目集合R(Iux)。其次，把该集合中所有项目的评分数据作为RBF神经网络的样本输入，训练网络的样本输出为ux对目标项目的评分Px,k，如图6所示。经过训练建立起来的网络就是基于用户ux评分的网络模型，记作net(ux)。

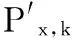
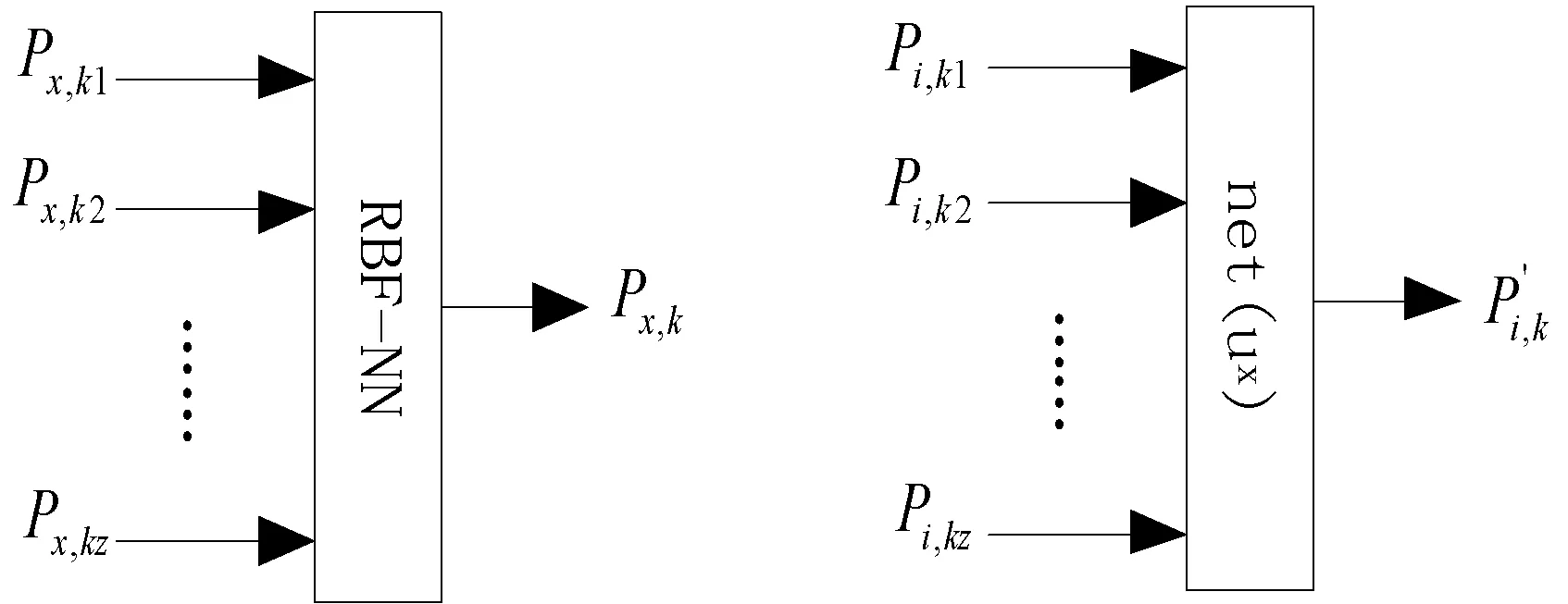
图6 基于ux评分的网络模型 图7 基于ux评分的网络输出

(4) 判断ux是否是集合T(ui)的最后一个用户。如果不是，则返回执行步骤(2)，直到计算完所有的相似用户；如果是，则说明已经收集完了所有基于邻近用户评分的网络输出，接下来执行步骤(5)计算目标用户的最终评分。

(5) 收集完所有邻近用户的网络输出评分后，使用如下改进的公式来计算ui对目标项目的评分Pi,k：

(6)

算法的流程如图8所示。

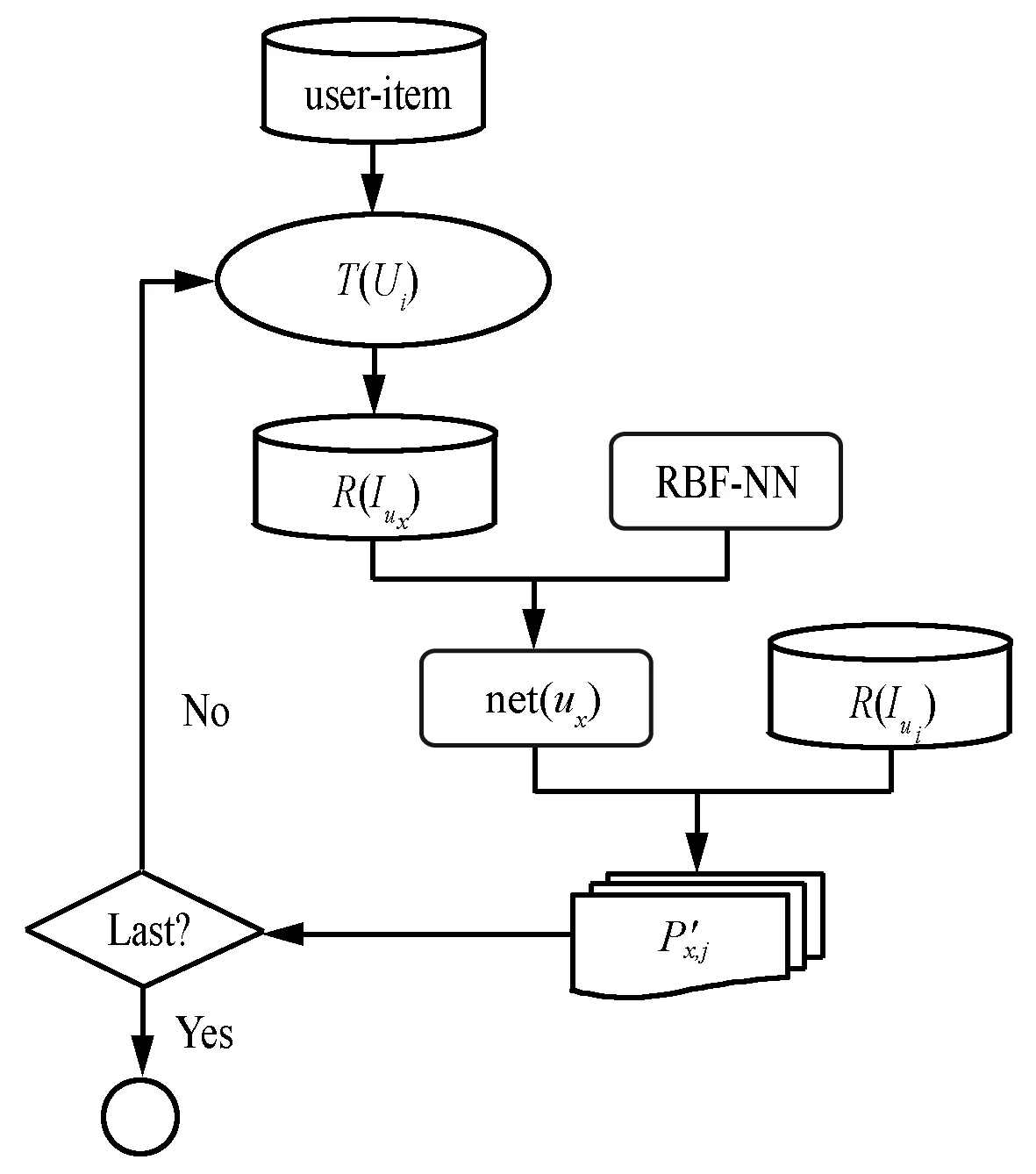
图8 基于RBF径向基的神经网络推荐算法流程图

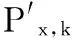
3 实验结果与分析

3.1 数据集

本文实验采用美国Minnesota大学的GroupLens项目小组创办的Movielens数据集。该数据集至少有10万条评分记录，包括943个用户对于1682部电影的评分。这里定义评分矩阵稀疏度为已有评分数量占影评总量的百分比。

3.2 度量标准

评价推荐系统推荐质量的度量标准大多采用统计精度度量方法[12]。该方法中的平均绝对偏差MAE(Mean Absolute Error)方法不仅易于理解，而且还可以直观地对推荐质量进行度量。故本文采用该方法作为评价度量标准。平均绝对偏差通过计算用户的预测评分与实际评分之间的偏差来度量预测的准确性[13]。MAE值大小与推荐质量之间成反比关系，也就是说MAE值越小，推荐质量就越高。

3.3 实验结果与分析

由于协同过滤推荐算法的推荐效果同时受到评分数据集稀疏度(λ)和邻近用户个数(N)两个因素的影响，所以，在验证改进算法时将围绕这两个因素进行对比。

(1) 不同评分数据稀疏度算法的对比

实验中对原始数据进行随机删减，形成λ分别为2%、4%、6%、10%、12%、14%、16%、18%和20%的10个稀疏评分矩阵，并分别对这10个评分矩阵使用传统的协同过滤推荐算法和本文提出的改进算法进行测试。这里固定邻近集合的大小为15，这样可以在相同邻近用户数量的情况下对比不同评分稀疏性对评分预测所带来的影响。实验所测的数据如表4所示。

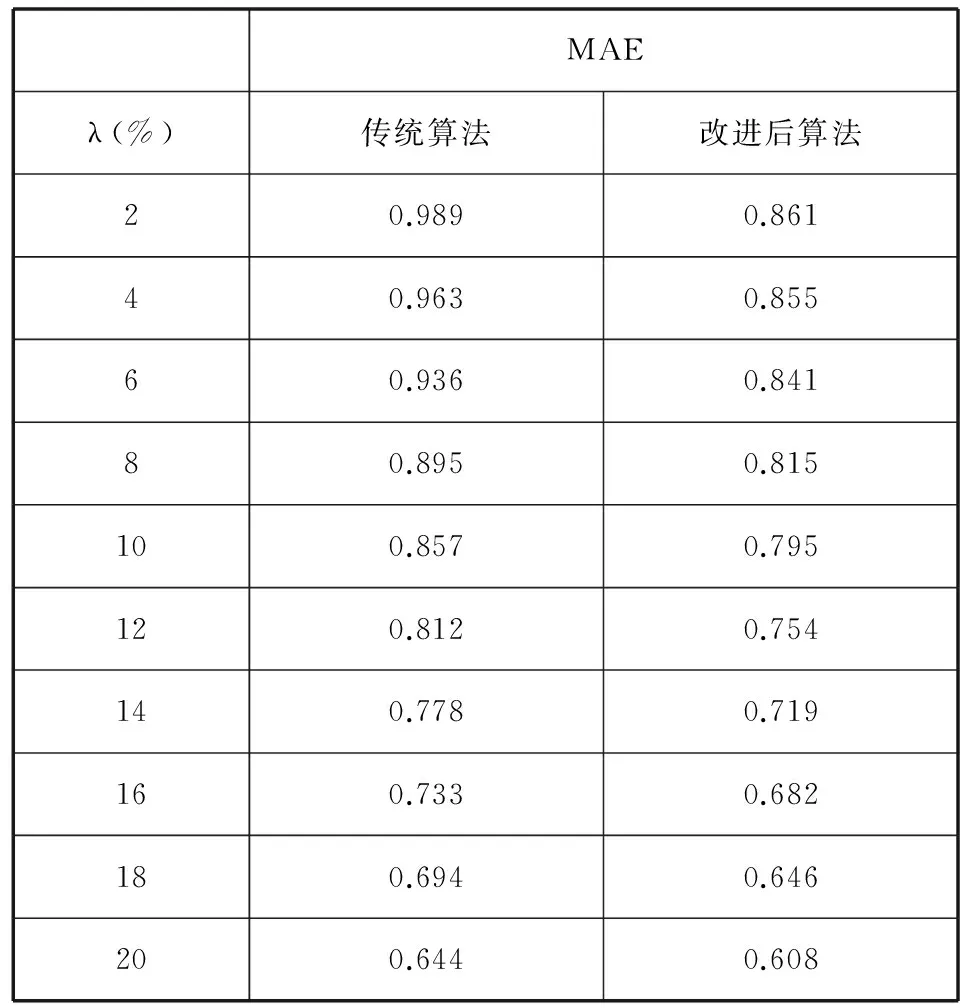
表4 不同评分数据稀疏度下的MAE值

图9为按照表4所作的直观对比实验结果。

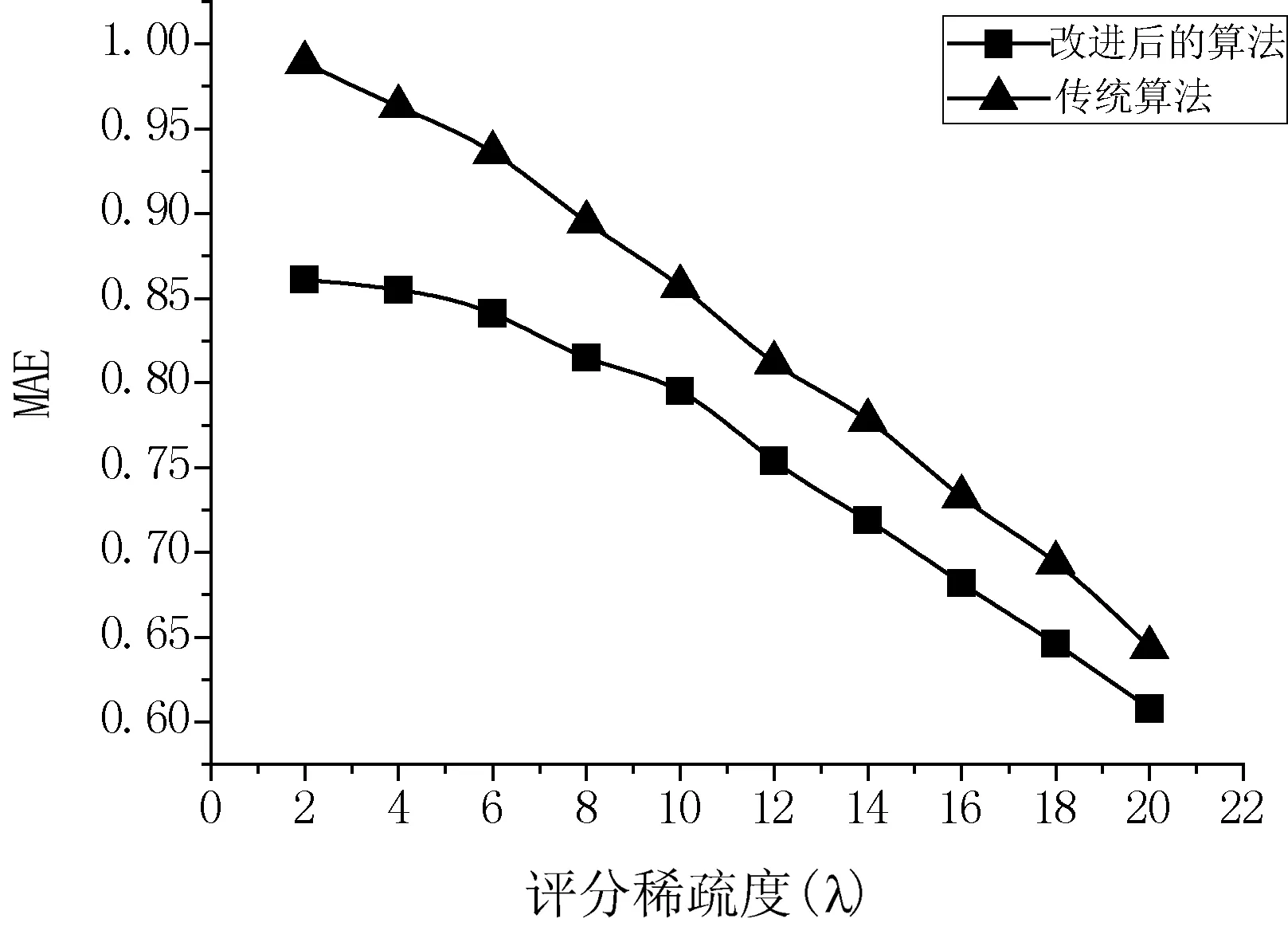
图9 不同评分数据稀疏度结果对比图

从图9可以看出，当评分矩阵密度越小时，改进后的协同过滤算法的MAE值比原协同过滤算法的值小。当密度不断增大时，这两种算法之间的MAE值不断接近。这是因为在固定邻近用户数量的情况下，当评分数据越稀疏时，所得到的邻近用户与目标用户之间相似度可靠性就越低。可靠性低的邻近用户在对目标项目的评分上产生过高或者过低的偶然性因素的概率就会越高。相反，当评分密度大时，计算所得到的目标用户与邻近用户相似的可靠性也就越高，所以邻近用户与目标用户之间就更加相似，那么评分上的偶然性因素发生的概率就会降低。

(2) 不同邻近用户数量上算法的对比

在同一评分数据稀疏度，不同邻近用户数量下传统算法和改进后算法的对比实验中，邻近用户数量分别取5、15、25、35、45, λ固定为10%。实验所测得的数据如表5和图10所示。

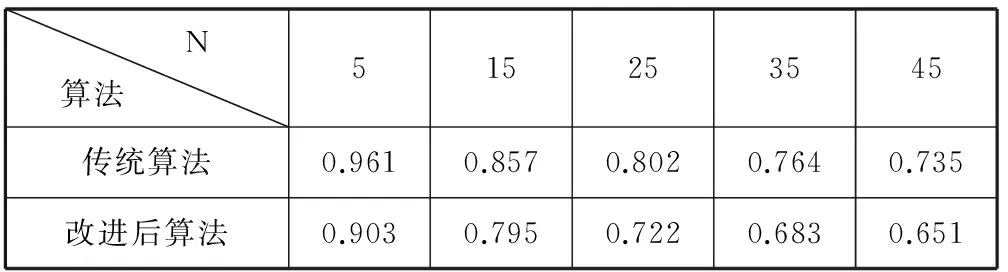
表5 不同邻近用户数量下的MAE值

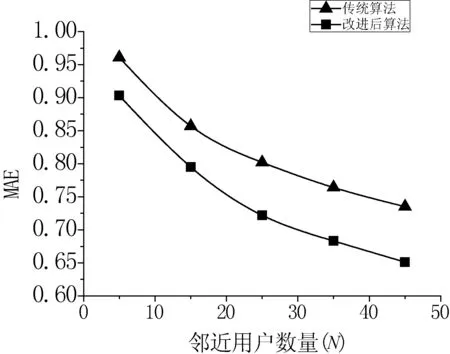
图10 不同邻近用户数量下MAE值对比图

从图10中看出，随着邻近用户数量的不断增多，两种算法的MAE值都呈现了下降的趋势，但改进后的算法要比传统的算法下降得快一些。这说明改进后的算法在邻近用户数量越多时性能越好。分析原因，主要是在固定评分数据稀疏度下，随着用于计算的邻近用户数量的增多，邻近用户与目标用户的相似度会越来越小，用户之间相似可靠性也会随之下降，导致邻近用户与目标用户在目标项目上的评分差值增大。而使用改进后的算法能够减小这两个用户对目标项目评分之间的差值，从而提高了预测的精确度。

4 结 语

针对邻近用户对目标项目评分上的偶然性偏大或者偏小因素给目标用户的预测结果带来误差的情况，本文使用了RBF径向基神经网络对传统的协同过滤推荐算法进行改进。改进后的算法在传统算法的基础上结合了目标用户自身的评分特性，达到了减小预测值与真实值之间评分偏差的目的，进而降低了邻近用户对目标项目评分过高或者过低所带来的偶然性误差。实验结果表明，与传统推荐算法相比，改进后的推荐算法在数据评分稀疏和邻近用户数量大的情况下可以获得更好的推荐效果。

改进后的算法在原有算法的基础上增加了对邻近用户评分建模这一步骤。如果单个邻近用户评分项目数量比较多的时，必然会增加网络的训练时间，从而算法的运行整体运行效率会大大地降低。在将来的工作中将研究如何对邻近用户的项目评分数据进行优化，提升RBF神经网络模型建模效率，降低改进后算法运行的代价。

[1] Hu L,Song G H,Xie Z Z,et al.Personalized recommendation algorithm based on preference features[J].Tsinghua Science & Technology,2014,19(3):293-299.

[2] 郭磊,马军,陈竹敏,等.一种结合推荐对象间关联关系的社会化推荐算法[J].计算机学报,2014,37(1):219-228.

[3] 马宏伟,张光卫,李鹏.协同过滤推荐算法综述[J].小型微型计算机系统,2009,30(7):1282-1288.

[4] 邓晓懿,金淳,韩庆平,等.基于情境聚类和用户评级的协同过滤推荐模型[J].系统工程理论与实践,2013,33(11):2945-2953.

[5] 黄创光,印鉴,汪静,等.不确定近邻的协同过滤推荐算法[J].计算机学报,2010,33(8):1369-1377.

[6] 杨杰.个性化推荐系统应用与研究[D].合肥:中国科学技术大学,2009:16-22.

[7] Yigit M,Bilgin B E,Karahoca A.Extended topology based recommendation system for unidirectional social networks[J].Expert Systems with Applications,2015,42(7):3653-3661.

[8] Zhang Y,Liu Y D,Zhao J.Vector similarity measurement method[J].Technical Acoustics,2009,28(4):532-536.

[9] Qiao Junfei,Han Honggui.Optimal Structure Design for RBFNN Structure[J].Acta Automatica Sinica,2010,36(6):865-872.

[10] 周维华.RBF神经网络隐层结构与参数优化研究[D].上海:华东理工大学,2014:13-21.

[11] 刘金琨.RBF神经网络自适应控制MATLAB仿真[M].北京:清华大学出版社,2014:227-280.

[12] 刘淇.基于用户兴趣建模的推荐方法及应用研究[D].合肥:中国科学技术大学,2013:33-58.

[13] 杨芳,潘一飞,李杰,等.一种改进的协同过滤推荐算法[J].河北工业大学学报,2010,39(3):82-87.

A NEW COLLABORATIVE FILTERING RECOMMENDATION ALGORITHM BASED ON RBF NEURAL NETWORK

Ye Lanping Liu Feng Zhu Erzhou*

(SchoolofComputerScienceandTechnology,AnhuiUniversity,Hefei230601,Anhui,China)

Traditional collaborative filtering recommendation algorithms have the problem of over dependence on neighbouring users in the prediction of target users’ rating while neglecting the rating characteristic of target users themselves. Aiming at the problem, this paper proposes an improved RBF-based neural network prediction method. The method uses RBF (radial basis function) neural network to carry out model training on the projects rating data of neighbouring users first, and gets the target user-based network rating model; then it calculates in combination with the rating of target user its own to obtain a rating result which is based on the model; at last, it combines the model ratings of all the neighbouring users to predict the final rating of target user on target items. The improved algorithm learns from the similarity between neighbouring users and considers the rating characteristics of target user its own as well. Experimental results show that the improved collaborative filtering recommendation algorithm is able to achieve better recommendation results than the traditional algorithms.

Collaborative filtering Rating deviation RBF neural network User rating data model

2015-05-16。国家自然科学基金项目(61300169)。叶兰平，硕士生，主研领域：智能计算。刘锋，教授。朱二周，讲师。

TP301.6

A

10.3969/j.issn.1000-386x.2016.11.042