基于递减反馈视野的人工鱼群算法改进与应用

王 丽 宫建平

(晋中学院信息技术与工程学院 山西 晋中 030619)



基于递减反馈视野的人工鱼群算法改进与应用

王 丽 宫建平

(晋中学院信息技术与工程学院 山西 晋中 030619)

基本人工鱼群算法的觅食行为是算法收敛的基础，觅食视野固定会导致寻优效率低、易陷入局部极值等弊端。引入视野递减反馈策略，视野随着迭代次数和寻优的反馈信息适时变化，旨在平衡算法的全局搜索和局部搜索能力。通过五个TSP实例测试，结果表明该算法在保证收敛速度的基础上提高了计算精度。最后将改进算法应用于求解山西省国家AAAA级风景区(含5A)最短遍历路径问题。

鱼群算法 递减视野 反馈策略 最优路径

0 引 言

水域中鱼类生存数目最多的地方意味着食物最多，人工鱼群算法AFSA(artificial fish swarm algorithm)就是模仿鱼类群体行为方式提出的一种基于动物自治体的优化方法[1]。该算法通过模拟鱼类的觅食、聚群、追尾和随机等行为在搜索区域内进行寻优，每条人工鱼通过感知外界环境和其他人工鱼的状态调整自身的行为。它对初值参数选择不敏感，对目标函数的要求极低，对待求问题的适应能力很强，可以解决经典优化方法不能求解的带有绝对值且不可导二元函数的极值问题。但随着优化问题复杂程度和搜索空间维度的增加，后期的收敛速度明显减小，只能找到较优解域，很难得出精确的最优解。近年来许多学者从多方面对算法进行改进，大致可以分成三类：与待求实际问题结合对算法行为改进[2,3]、与其他算法结合进行分段优化或者混合优化[4-6]、对算法相关参数进行改进[7,8]。例如文献[2]将速度引力场与人工鱼群算法结合，在多变的复杂环境中追踪动态目标，对所生成路径进行评估和修正，从而获得最优路径；文献[3]求解旅行商问题时将城市间距离作为启发式信息来加快人工鱼寻优的速度；文献[4]和文献[5]分别将和声搜索算法和微粒群算法与人工鱼群算法进行融合；文献[6]对基本人工鱼群算法的移动条件进行改进，并且采用分段优化的方法；文献[7]和文献[8]分别针对人工鱼群算法视野和步长进行自适应调整；为了使算法在迭代初期具有良好的全局探索性，而在迭代后期具有较优的局部搜优性，文献[9]将高斯变异和柯西变异的优点结合，形成一种新的自适应t变异机制，并将变异机制应用于种群中的非最优个体，同时针对种群中的最优个体执行高斯最优调教变异。大量文献经实验发现，如果视野较大，那么算法前期收敛速度很快。但在算法后期，人工鱼个体在较优解域附近仍以此视野觅食就无法搜索到全局最优解或者陷入局部极值点。视野较小又会导致寻优迭代次数太大，很难找到一个折中的视野参数来兼顾整个迭代过程的搜优效率。为了提高算法后期的求解精度，文献[10]使鱼群个体的步长和视野逐渐递减到一个固定值，提出了一种基于Logistic模型的变步长和变视野机制的改进人工鱼群算法。本文受文献[7]的启发在AFSA的基础上引入递减指数和迭代阈值，提出一种基于视野递减反馈策略的改进人工鱼群算法，旨在保证算法前期的收敛速度和算法后期的收敛精度，同时也能避免算法后期陷入局部最优，有利于提高搜索效率和准确性。最后将其应用于解决最短遍历路径问题。

1 改进的人工鱼群算法

1.1 基本人工鱼群算法求解TSP的思想

人工鱼群算法模仿鱼类的觅食行为、聚群行为、追尾行为和随机行为构造人工鱼群，通过四种行为使得几个局部极值甚至全局最优值周围可以聚集大量人工鱼。每条人工鱼对应一个优化解，食物浓度对应目标函数。假设有N条人工鱼，每条人工鱼的状态为向量X=(x1,x2,…,xn)，人工鱼当前位置的食物浓度为Y=f(X)，人工鱼个体之间的距离为di,j=‖Xi-Xj‖。

TSP一直是组合优化领域研究的经典热点问题之一，常常被用来验证智能启发式算法的有效性。一个旅行商人从某城市出发，选择一条遍历所有城市节点最短的路径，最终返回出发城市，限制路径中每个城市只能拜访一次。其数学模型为：假设有n个城市C=(C1,C2,…,Cn),城市之间的两两距离为di,j=(Ci,Cj)。设路径距离为F,则目标函数为：

(1)

基于此，人工鱼群算法是求解TSP问题的一个有效方法。

1.2 递减反馈策略

本文经多次实验发现，觅食行为的视野对收敛速度影响较大，而且大视野可使人工鱼的全局搜索能力强，觅食行为较频繁；小视野可使局部搜索能力强，觅食行为减弱而追尾行为相对频繁。故本文以最大迭代次数M的一半为界，将整个迭代过程分为前期和后期，在迭代前期将觅食行为的初始视野V0设置为较大值。为了减小算法陷入局部极值点邻域无法跳出的概率，视野随着迭代数的增加呈指数式递减，当迭代次数达到阈值K时将视野范围限定为终止视野Vf。视野递减策略公式为：

(2)

其中k为当前迭代数，λ为递减指数。因为人工鱼只和视野内的其他个体交流信息，所以随着视野逐渐减小，会形成几个孤立的子鱼群。为了防止算法陷入局部极值，继而设置反馈策略：若从K+1代开始至M/2代时无更优解，则迭代后期将视野重新设定回初始值V0，V(M/2)+1=V0依次按照式(3)变化；反之，视野仍限定为Vf。

(3)

另外，人工鱼行为方式的选择采用目标函数最小的准则。基本鱼群算法中的缺省行为为随机行为，存在迂回搜索的弊端，降低寻优速度，本文将随机行为改进为停止行为。

1.3 改进算法流程

步骤1鱼群初始化。设置鱼群规模为N、最大迭代次数M、人工鱼的移动步长Step、觅食行为的最大试探次数try_number和拥挤度因子δ。当迭代次数从k=0开始计数时，生成N条人工鱼个体，即初始鱼群，每条人工鱼代表待优化问题的路径，是在给定范围内产生的随机实数数组。设待优化问题为n元参数，则要产生一个n行N列的初始序列，每列表示每条人工鱼的n个参数。

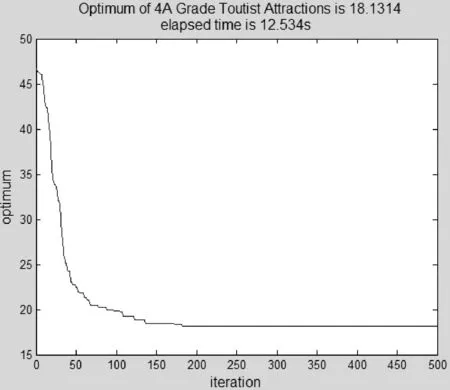
步骤2公告板初始化。计算人工鱼群的目标函数值，并将最优鱼状态写入公告板。

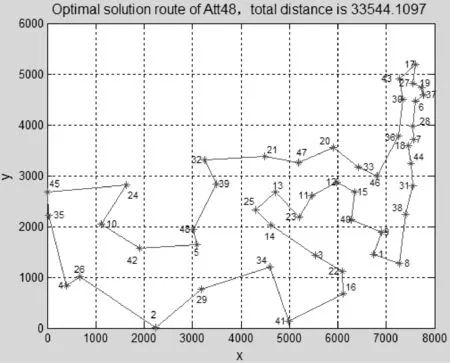
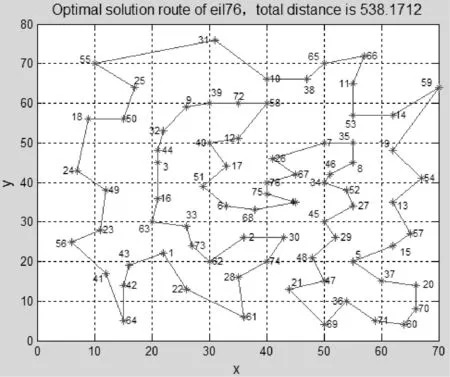
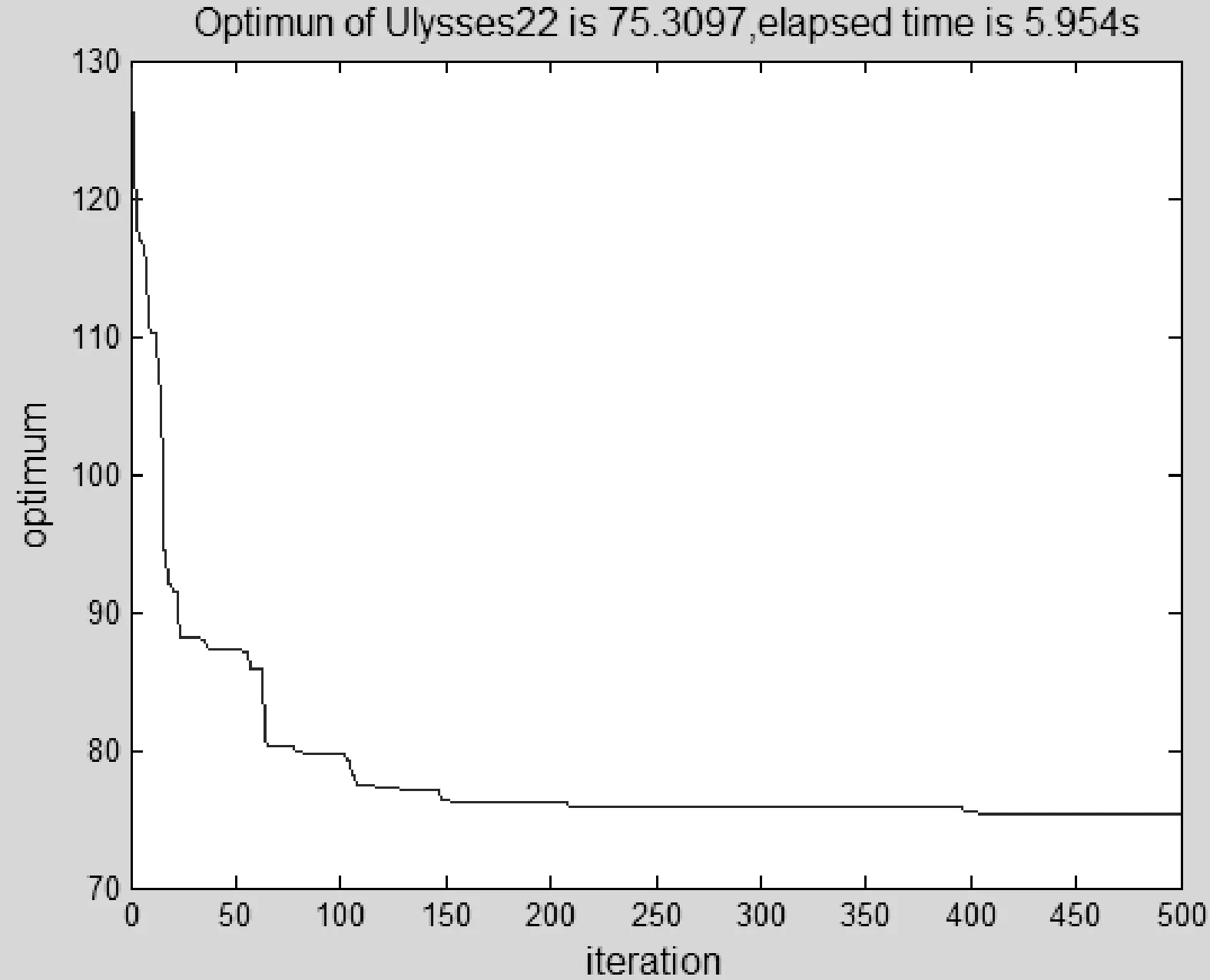
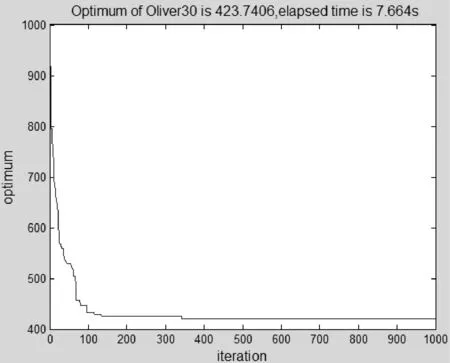
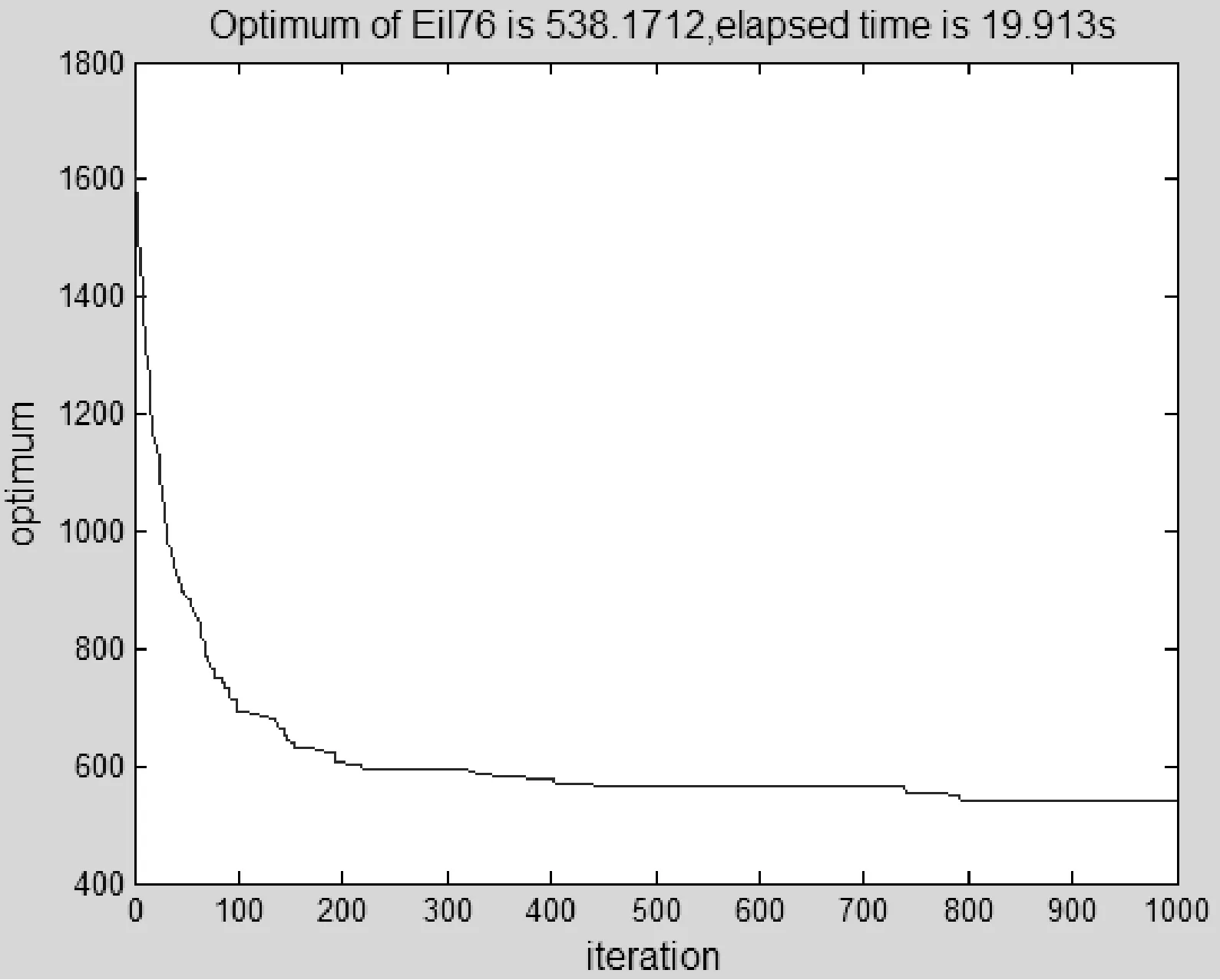
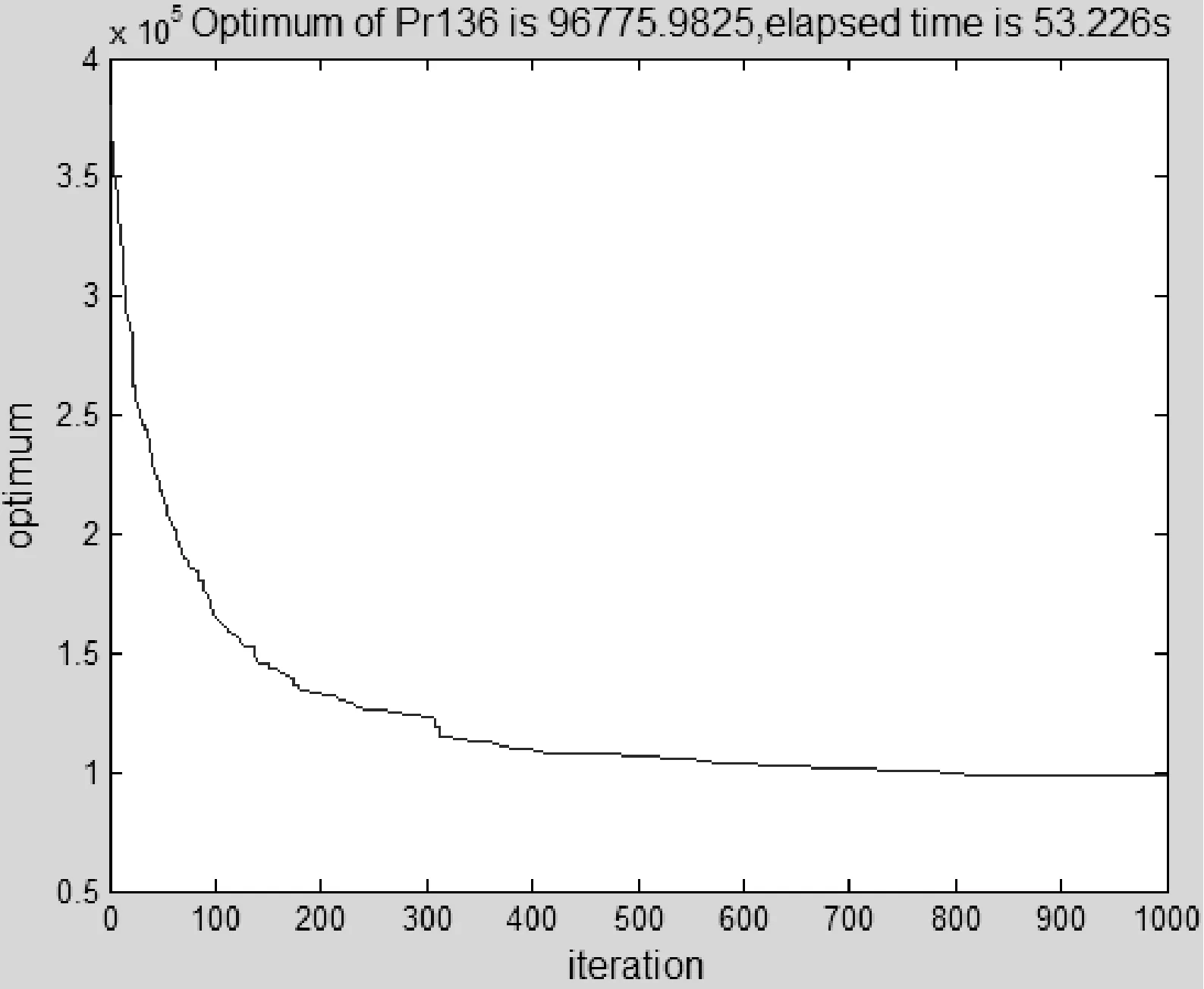
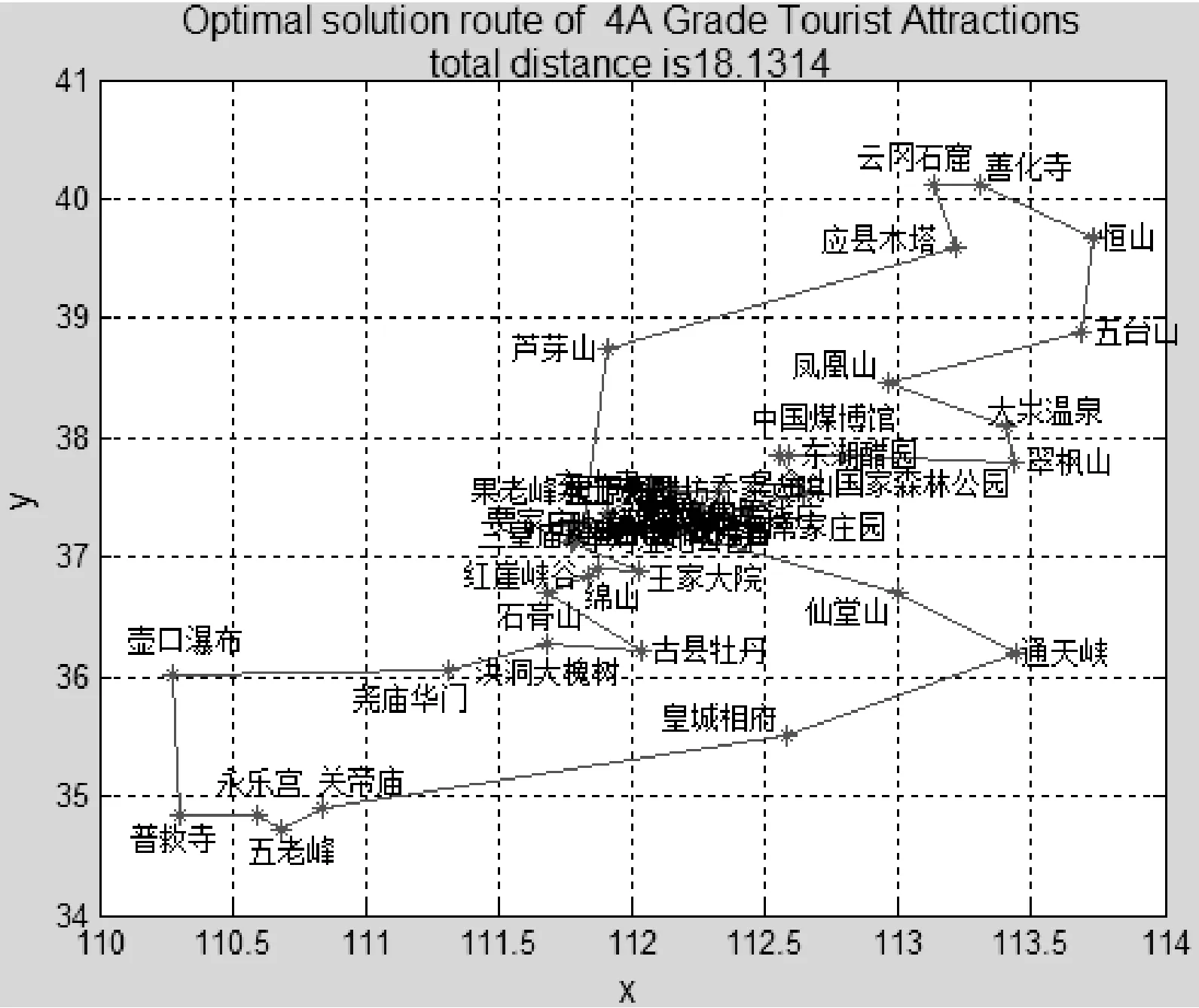
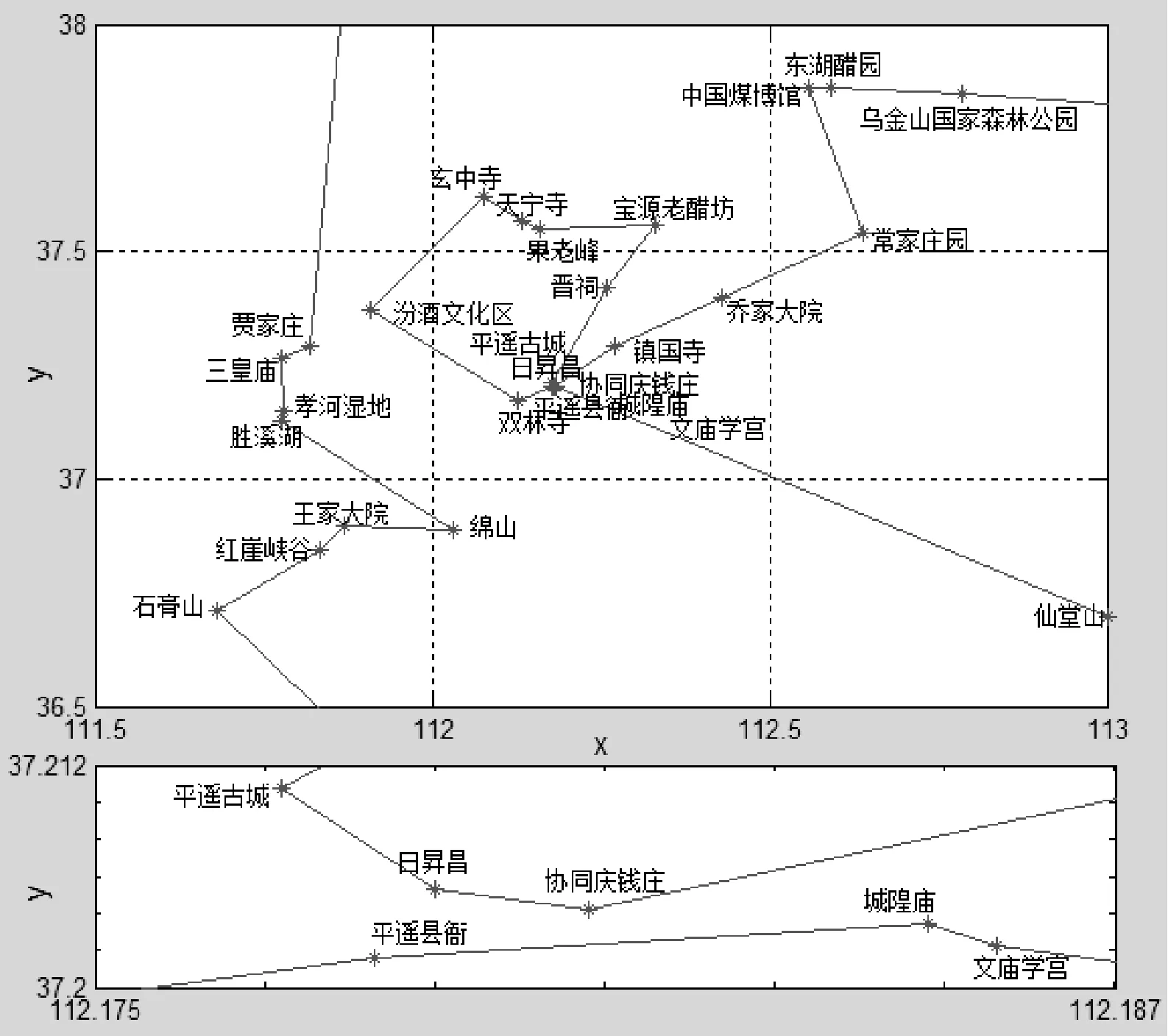
步骤3追尾行为和群聚行为。设人工鱼的当前状态为Xi，在其视野范围内探测邻居数目n以及状态最优的邻居Xj、中心位置Xc。若此邻居的食物浓度较高且周围不太拥挤，即Yj

(4)

若Yc

(5)

比较两种行为的寻优结果，择优而行。若两种行为都没有使食物浓度提高，则执行觅食行为(其中Y表示食物浓度，即目标函数)否则执行觅食行为。

步骤4觅食行为。设人工鱼当前状态Xi，在视野内随机选择状态Xl=Xi+rand()·Visual，视野初始值设为V0，随着迭代次数按照式(2)和式(3)变化。若Yl>Yi,则向该方向前进一步，否则维持当前状态不动。判断是否满足前进条件，若尝试次数达到try_number仍不能前行，则随机移动一步。

(6)

步骤5判断是否达到终止条件(迭代次数达到M或寻优结果满足精度要求)，若是，则更新公告板，输出最优结果，算法终止；若否，则进入下一次迭代过程。

2 仿真实验及应用

2.1 算例及参数选取

为了验证引入递减反馈策略人工鱼群算法的有效性和先进性，本文从TSPLIB选取Ulysses22、Oliver30、Att48、eil76和Pr136五个标准TSP实例进行测试(http://elib.zib.de/pub/Packages/mp-testdata/tsp/tsplib/tsp/)。TSP问题所选择的路径数目与城市规模呈指数式增长的关系，当城市规模较小时用最简单的枚举法即可获得最短路径；当城市数目较大时，多数算法无法获得全局最优解，往往以算法的最优解与TSPLIB给出的最优解之接近程度作为算法计算精度之考量。本文采用Matlab 7.1为编程工具实现算法，实验分别用基本鱼群算法AFSA和改进算法各自进行20次测试，并将求解结果与文献进行对比。参数设置为：人工鱼数目N=10，Ulysses22的最大迭代次数M设为500，Oliver30、Att48、eil76和Pr136的最大迭代次数M设为1000，最多试探次数try_number=15，拥挤度因子δ=0.618。本文引入的反馈递减策略参数包括初始视野V0、终止视野Vf、迭代阈值K、递减指数λ、步长step。经过多次实验对比，五个TSP实例对应的最优参数集{V0,Vf,K,λ,step}分别设置为：{1.5,0.3,80,2,Vk/3}{2.5,0.5,300,2.2,Vk/5}{2.8,0.6,600,2.8,Vk/20}{5,1,630,1.5,Vk/2}{20,2,280,1.5,Vk/4}。

2.2 实验结果分析

五个TSP实例求解结果如表1所示。TSPLIB给出的五个标准TSP问题全局最优解分别为74、420、33 522、538和96 772。前三个TSP实例求解结果与文献[3]的改进鱼群算法对比，后两个TSP实例与文献[11]的改进蚁群算法对比。收敛率定义为：20次实验中收敛次数与实验次数之比，每次运行的最终解和全局最优解误差在3.5%之内则认为算法收敛。由表1计算结果可看出：对于同一TSP问题，利用本文改进算法求解的最优值最接近TSPLIB所给结果，相对误差分别为1.7699%、0.8906%、0.1966%、0.0318%和0.0041%，说明本文算法在计算精度方面有所提高。纵向对比五个TSP问题的城市数目与其平均相对误差之关系，利用基本鱼群算法两者关系为近似正比，而文献[3，11]和本文改进算法为近似反比，并且本文改进算法的平均相对误差更小，分别为2.0657%、0.9758%、1.3825%、0.3183%和0.3154%，说明本文改进算法具有较高的求解精度，尤其在求解较大规模TSP问题中更能体现出先进性。基本鱼群算法的收敛率随着TSP问题复杂程度增加而迅速减小为0，当城市数目达到48时，文献[9]的改进算法收敛率急剧降低至25%，而利用本文改进鱼群算法求解结果全部满足收敛条件(表1中，——表示该数据该文献未提及)。

表1 五个TSP实例求解结果

五个TSP问题的最优解巡回路径分别如图1-图5所示，图中横坐标和纵坐标分别表示城市的经度和纬度，单位为弧度(下同)。五个TSP问题的最优解收敛曲线分别如图6-图10所示，横坐标和纵坐标分别表示迭代次数和最优值。

图1 Ulysses22的最优解巡回路径

图2 Oliver30的最优解巡回路径

图3 Att48的最优解巡回路径

图4 eil76的最优解巡回路径

图5 Pr136的最优解巡回路径

图6 Ulysses22的最优解收敛曲线

图7 Oliver30的最优解收敛曲线

图9 Eil76的最优解收敛曲线

图10 Pr136的最优解收敛曲线

由改进算法的收敛曲线图可看出，视野递减策略使算法初期的迭代曲线非常陡峭，算法可以很快找到局部最优解，意味着改进算法保证了初期具有较好的搜优速度，而且并未出现明显的振荡现象。另外，五个TSP实例运行20次的迭代次数范围不大，分别为[338,408]、[296,364]、[756,818]、[749，803]和[754,815]，说明改进算法具备稳定的全局搜优性能。

3 改进算法求解最短遍历路径

本文改进算法研究目的是为了更好地应用于实际问题求解。截止2014年12月底，国家旅游局评定出山西省4A(含5A)级旅游景区共47处，其中4A级旅游区42处，5A级旅游景区5处，位置分布及局部放大图如图11所示。这些风景区分布在山西省各地，是全省旅游资源的精华所在。假设一个外地旅行者，从山西省任一处4A级景点出发，每个景点去一次且仅去一次，游览完所有景点返回出发点，希望路线总长度最短，需要在最短的时间内规划一条最佳出行路线。本文改进算法可以很好地解决山西省国家4A级以上风景区为地点构成的TSP问题。设置人工鱼数目N=10，最大迭代次数M=500，最多试探次数try_number=15，拥挤度因子δ=0.618，经过多次实验对比，最优参数集设置为{4,1.5,100,1.8,Vk/10}，最优解的巡回路径和收敛曲线分别如图12和图14所示。因晋中市4A级景区分布较为集中，利用Matlab放大镜功能需要将图11中经度[111.5,113]和纬度[36.5,38]区域、经度[112.175,112.187]和纬度[37.2,37.212]区域进行局部放大，如图13所示。计算结果如下：20次运算过程迭代次数范围为[243,378]，平均迭代次数329.18，最优解为18.1314，最差解为21.7717，平均值为19.0816；按照巡回路径最优解输入各景点的经纬度，在Matlab中调用distance 函数计算出最短遍历路径长度为 1658.12798 km。

图11 山西省4A(含5A)级旅游景区分布图

图12 山西省4A(含5A)级风景区最优解巡回路径

图13 图12的局部放大图

图14 山西省4A(含5A)级风景区最优解收敛曲线

4 结 语

本文在基本鱼群算法的基础上引入递减指数λ和迭代阈值K，对觅食行为的视野设置递减反馈策略：为了保证算法的寻优速度，视野初值设置为较大值；为了提高计算精度，视野在优化过程前期随迭代次数递减；为了避免陷入局部极值，在优化过程后期设置反馈策略，视野根据反馈信息适时变化。通过对五个具有代表性的TSP实例进行仿真实验，并与基本鱼群算法以及其他文献改进算法结果对比分析，寻优过程和仿真结果表明：本文提出的改进鱼群算法在搜优精度、收敛速度、稳定性等方面有明显优势。最后将其应用于求解最短遍历路径问题。然而改进算法的视野最优参数集直接影响算法性能，本文选取的参数只是在有限次实验对比过程中相对最优，所以亟需进一步研究最优视野参数集选取的合理方法。

[1] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002(11):32-38.

[2] 陈廷斌,张奇松,杨晓光.基于改进人工势场—鱼群算法的LBS最短路径修正研究[J].计算机应用与软件,2015,32(6):259-262.

[3] 朱命昊,厍向阳.求解旅行商问题的改进人工鱼群算法[J].计算机应用研究,2010,27(10):3734-3736.

[4] 张洪青,卜涛.基于和声搜索的混合人工鱼群算法[J].计算机应用与软件,2014,31(3):269-272,285.

[5] 孙伟,朱正礼,郑磊,等.基于人工鱼群和微粒群混合算法的WSN节点部署策略[J].计算机科学,2012,39(11):83-85,121.

[6] Zhou Yongquan,Huang Huajuan,Zhang Junli.Hybrid artificial fish swarm algorithm for solving Ill-Conditioned linear systems of equations[J].Intelligent Computing and Information Science,2011:656-661.

[7] Ma Xianmin,Liu Ni.Improved artificial fish swarm algorithm based on adaptive vision for solving the shortest path problem[J].Journal on Communications,2014,35(1):1-6.

[8] 朱旭辉,倪志伟,程美英.变步长自适应的改进人工鱼群算法[J].计算机科学,2015,42(2):210-216,246.

[9] 王波.基于自适应t分布混合变异的人工鱼群算法[J].计算机工程与科学,2013,35(4):120-124.

[10] 王培崇,李丽荣,贺毅朝,等.一种基于Logistic模型的人工鱼群算法[J].中国科技论文,2013,8(7):668-671.

[11] 宋锦娟,白艳萍.一种改进的蚁群算法及其在TSP中的应用[J].数学的实践与认识,2012,42(18):154-162.

IMPROVING ARTIFICIAL FISH SWARM ALGORITHM BASED ON DEGRESSION FEEDBACK VISION AND ITS APPLICATION

Wang li Gong Jianping

(School of Information Technology and Engineering,Jinzhong University,Jinzhong 030619,Shanxi,China)

Foraging behaviour of basic artificial fish swarm algorithm is the basis of algorithm convergence. A fixed foraging vision may lead to the disadvantages of low optimising efficiency and being prone to local extremums. To overcome such disadvantages, we introduced the vision degression feedback strategy, in which the visual field timely changes along with the times of iteration and the feedback information of optimisation aiming at balancing global and local search abilities. By testing five TSP examples, results suggested that the proposed algorithm improves the calculation accuracy while ensuring the convergence rate. At last, we applied the improved algorithm to solving the problem of the shortest path traversal of AAAA grade tourist attractions (including 5A) in Shanxi province.

Artificial fish swarm algorithm Degression of vision Feedback strategy Optimal path

2015-09-02。教育部高等学校专业教学指导委员会项目(JZW-14-JW-09)；山西省高等学校教学改革项目(J2014108)；晋中学院教学改革创新项目(ZL2016jg04)。王丽，讲师，主研领域：智能优化算法，计算物理。宫建平，教授。

TP18

A

10.3969/j.issn.1000-386x.2016.11.053