基于稀疏学习的鲁棒自表达属性选择算法

何 威 刘星毅 程德波 胡荣耀

1(广西师范大学广西多源信息挖掘与安全重点实验室 广西 桂林 541004)2(广西钦州学院 广西 钦州 535000)



基于稀疏学习的鲁棒自表达属性选择算法

何 威1刘星毅2*程德波1胡荣耀1

1(广西师范大学广西多源信息挖掘与安全重点实验室 广西 桂林 541004)2(广西钦州学院 广西 钦州 535000)

受属性选择处理高维数据表现的高效性和低秩自表达方法在子空间聚类上成功运用的启发，提出一种基于稀疏学习的自表达属性选择算法。算法首先将每个属性用其他属性线性表示得到自表达系数矩阵；然后结合稀疏学习的理论(即整合L2,1-范数为稀疏正则化项惩罚目标函数)实现属性选择。在以分类准确率和方差作为评价指标下，相比其他算法，实验结果表明该算法可更高效地选择出重要属性，且显示出非常好的鲁棒性。

高维数据 属性选择 属性自表达 稀疏学习

0 引 言

在机器学习和数据挖掘的分类任务中，往往需要处理大量的高维数据，其中无关或冗余的属性会对分类性能产生严重影响。属性选择方法能选择出小部分重要属性作为新的属性集，并能维持甚至提高分类性能[1]，因而在机器学习领域得到了广泛的应用。常见的属性选择方法有：有监督方法、无监督和半监督方法[13]。有监督的属性选择方法通过已知的类标签，对训练结果测试，从而进行属性的重要性评估，常见的方法有t检验法和稀疏正则化线性回归等[14]。无监督的属性选择，没有指导最小特征子集选择的类标签信息。无监督属性选择方法，主要使用一些评价指标，如方差[5]、拉普拉斯算子分值[7]或秩比率[15]等，来评估每一个单独的特征或特征子集，然后选择最重要的前k个特征或最佳特征子集。这些指标可评价聚类性能、冗余、信息损失、样本相似性或流形结构等。但是，在使用这些方法对所有属性进行搜索时，计算复杂度过高，不能适用于高维大数据。半监督方法是有监督与无监督方法的结合，主要利用少量有标签样本和大量的无标签样本进行训练和分类，如：自训练算法、多视图算法[13]。本文研究无监督属性选择方法。

在属性选择方法中，L2,1-范数的组稀疏正则化已被成功应用，且在各种实际应用中表现出了良好的性能[6]。在自然界中，自相似性是普遍存在的，即一个对象的一部分与其本身的其他部分相似。研究发现，拥有自相似性质的对象，每个属性可以近似表示为其自身属性的线性组合，称之为自表达。基于对象的自相似性的性质，自表达性质适用于大多数的高维数据，并已广泛应用于机器学习和计算机视觉领域[11]。而在无监督的属性选择中，由于没有类标签指导，很难获得最小属性子空间[4]。本文提出特征的自表达属性方法，即每个属性通过用其他属性来表征，更好地利用了数据的内部特征，从而解决了无监督属性选择方法中，无类标签的特点。基于以上考虑，本文利用特征的自我表达能力，特征矩阵代表本身寻找有代表性的特征成分，并结合稀疏学习以达到良好的效果。

1 相关理论背景及简介

稀疏学习[2]最早应用于图形、图像视觉等领域。由于具有强大的内在理论及应用价值，所以稀疏学习得到了迅速的发展，并在模式识别与机器学习等领域得到广泛的应用。

设W∈Rn×1是模型的参数向量，n是样本数，其中，w1,w2,…,wn表示n个样本参数，且W=[w1，w2，…，wn]。本质上，数据的特点是由少量关键特征决定的。属性选择的目标是找出一个有代表性的特征子集，所有属性都能通过它来重建。鉴于稀疏学习可实现特征的自动选择，为此本文算法采用稀疏学习的方法，来自动选择重要的特征子集。在稀疏学习的基本理论中，首先通过对模型的参数向量w∈Rn进行一种稀疏假设，再用训练样本对参数w进行拟合，主要实现的目标函数为：

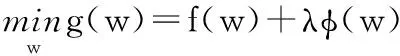
(1)

其中，f(x)是损失函数，φ(w)是正则化项，λ调节w的稀疏性，且λ越大，w越稀疏，反之亦然。

将稀疏学习应用于属性选择算法当中，能够将原始数据之间的系数权重作为重要的鉴别信息引入模型，通过稀疏约束来使得输入数据进行稀疏表示。这样可以去除冗余和不相关属性，同时保证重要属性能够被选择[9]。鉴于稀疏学习的正则化因子通常选用能够转化为凸优化问题来求解，故更能保证本文提出的模型求得唯一的全局最优解[3]。在稀疏学习中，L0-范数是最有效的稀疏正则因子，但因其求解为NP难，故很多文献均采用近似正则项L1-范数来替代L0-范数；而L2,1-范数能导致行稀疏，已经被证明比L1-范数更适合于属性选择[18]。L2,1-范数正则化因子能用于稀疏表示来获得组稀疏，因此本文采用L2,1-范数作为稀疏正则化因子来对属性自表达进行行稀疏处理，以达到剔除冗余和不相关属性的目的，且能够有效地减少离群点对结果的影响。

2 算法描述和优化方法

基于低秩自表达方法在子空间聚类上的成功运用，本文利用特征的自表达能力，提出了一种简单而且十分有效的无监督属性选择方法。通过属性自表达来构造自表达稀疏矩阵，然后采用稀疏学习的原理将冗余属性和不相关属性进行稀疏化处理，从而本文算法能够寻找出重要的特征成分。

假设给定训练集X∈Rn×m，其中，n和m分别表示样本数和属性数。xi代表第i个样本，即X=[x1,x2,…,xn]，然后利用fj代表第j个属性，即X=[f1,f2,…，fm]。早期的属性选择是利用一些度量来估计每个属性，比如协方差、拉普拉斯算子[7]等，然后通过得到的权值对所有属性进行排序，取前面的一部分属性作为新的属性集。在目前的一些方法[3,4,6]中，通常是先计算样本间的相似性或流行结构，然后建立一个响应矩阵Y=[y1,y2,…,ym]，使得属性选择问题转化为一个多输出的回归问题：

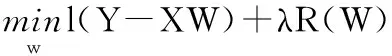
(2)

其中，W是属性权值矩阵，l(Y-XW)是损失函数，R(W)是关于W的正则化项，λ是正参数，用来调节对损失项的惩罚。

尽管式(2)是一种广泛应用的属性选择的方法，但在如何选取一个适当的响应矩阵时往往比较困难。因此，本文提出一种SR_FS(Self-Representation for Feature Selection)的属性选择算法。本文的算法使用X作为响应矩阵，其中Y=X，即利用属性自表达的方法，使得每个属性都能被全体属性很好地表现出来。即X中的每个属性fi，均能通过用全体属性(包括自身)的线性组合来表示：

(3)

其中ei为误差项，ωji为自表达系数。对于每个属性，可以将式(3)重写为：

X=XW+E

(4)

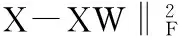
经以上属性自表达，可以得到自表达关系矩阵W。此时的W不能够很好地选择出重要的属性，而且为使得剩余量E尽可能接近于0，故本文算法添加一个有效的稀疏学习正则化来辅助属性选择。因此本文算法的模型可以重写为以下最小化问题：

(5)

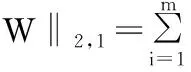
最终由式(5)就可以得到目标函数为：

(6)

其中，X∈Rn×d(n和d分别表示样本数和属性变量数)为训练样本，W∈Rd×d是关于X的系数矩阵，λ是调和参数。本文算法的伪代码如下：

算法1SR_FS算法

输入：训练样本，正则化参数λ。

输出：分类准确率。

1. 通过训练样本得出类指示矩阵X=[xi,k]；

3. 根据得到的W对原始属性集X进行属性选择，并将得到的属性集作为样本的新属性集；

4. 最后，对新属性集构成的样本采用SVM算法进行分类。

本文提出的算法具有如下优点：首先，由于算法采用了无监督属性选择模型的属性自表达方法，所以不需要标签矩阵Y来作为响应矩阵；其次，有效地将自表达学习和稀疏学习理论结合，该模型既能消除输入数据中的冗余和不相关的属性，又可实现特征的自动选择；最后，本文的目标函数提出了一种区别于交替方向乘子法的求解方法，该优化算法能保证目标值在每次迭代过程中减小，并趋近于全局最优解，最终求得全局最优解。

3 优化分析求解

由于式(6)的前半部分是凸的，且正则化项是非光滑的，本文设计了一种高效方法来求解式(6)。具体为，首先将式(6)对wi(1≤i≤m)求微分，且令其等于0，可以得到如下等式：

XTx(i)-XXTwi+λDiwi=0

(7)

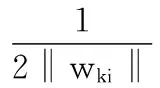
wi=(λDi+XXT)-1XTx(i)

(8)

注意Di是未知的且取决于W。由以上分析，并根据文献[12]和文献[8],本文提出算法2，用一种迭代方法来优化式(6)。

算法2优化求解式(6)的伪代码

输入:X;

输出: w(t)∈Rn×n;

1.初始化 W∈Rn×n,t=1;

2. while 未收敛 do

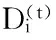
5.t=t+1;

6. 结束

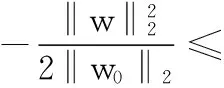
证明：根据算法2可得到

(9)

由此得到：

Tr(XTW(t+1)-X)T(XTW(t+1)-X)+

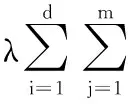
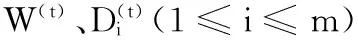
4 实验结果与分析

4.1 实验数据集和对比算法

本文用六个公开数据集测试提出的属性选择算法性能。为了测试本文算法的有效性和进行属性选择的效果，使用有标签的数据集来测试算法，并与其他对比算法进行比较测试。其中数据集madelon、DBWorld、train和musk来源于UCI数据集[15],TOX-171、warpAP10P来源于文献[16]，数据集详情如表1所示。

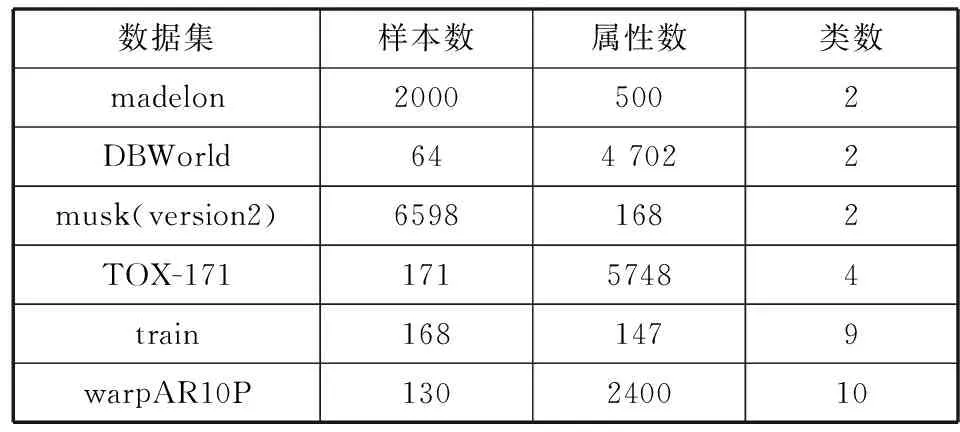
表1 数据集信息统计

本文实验是在Win7系统下的Matlab 2014a软件上进行编程实验。然后实验选择四种公认的有代表性的算法参与比较，包括:① NFS算法(Non Feature Selection)：对原始数据不做任何处理，直接使用LIBSVM工具箱[17]进行SVM分类，并作为实验的基准线；② PCA主成分分析方法(Principal Component Analysis)；③ LPP方法(Locality Preserving Projection)；④ RFS方法[9]：通过权值大小来表示属性重要性的强弱，损失函数和正则化项两者均采用L2,1-范数来约束。其中，NFS方法直接对原始数据集进行SVM分类[10]，未对原始数据进行任何处理，相比SR_FS等属性约简算法，不仅数据处理量大，而且结果容易受到冗余数据和噪音数据的影响；PCA考虑数据的主成分把数据从高维空间投影到低维空间，信息损失较为严重；LPP只考虑了数据的局部信息，没有考虑数据内部的整体情况，投影时信息损失也较为严重；RFS方法为产生稀疏系数矩阵，由此可以赋大权重给重要的属性，赋小权重给不重要的属性。在比较的算法中，PCA和LPP算法均属于子空间学习方法，RFS算法属于属性选择方法。

分析各算法的时间复杂度和空间复杂度。时间复杂度：本文SR_FS算法是稀疏学习与属性自表达的最小二乘的有效组合,其时间复杂度与PCA、LPP及RFS算法一致，同为O(n3)(其中n是样本量)；空间复杂度：本文算法与所有的对比算法均需存储矩阵乘法的中间结果，空间复杂度为线性。

4.2 实验结果和分析

本文首先用不同的算法对数据进行属性选择处理，然后用统一的方法对数据进行分类，并采用分类准确率作为评价指标，分类准确率越高表示算法效果越好，以此来检测是否提出的SR_FS算法能够具有很好的效果。实验通过10折交叉验证方法把原始数据划分为训练集和测试集，运用训练集通过算法来训练模型，用测试集测试模型的效果。实验采用SVM分类工具箱分类，得到分类准确率。所有的算法均保证在同一实验环境下进行，最后提取10次运行的实验结果的均值加减方差来评估各算法的分类效果和鲁棒性，具体各数据集实验结果见表2所示。为了比较不同数据量纲的各算法的鲁棒性，本文采用变异系数(变异系数=(标准差/平均值)× 100%)作为评价指标，统计结果见表3所示。为更直观地比较各算法的效果，每一数据集各算法每次的实验结果对比如图1-图6所示。

首先，分析表2数据可以看出，其中，SR_FS算法在不同数据集上取得的准确率均为最高，且与NFS算法比较平均提高了12.78%，效果最为明显，与RFS算法比较平均提高了3.35%。其中，在train数据集上，SR_FS对比其他算法准确率平均提升3.94%，为最低；而在musk数据集上效果最为显著，SR_FS与其他对比算法相比平均提高14.08%，且与NFS相比提高了19.1%。这是因为SR_FS算法不仅可以使属性自表达，而且同时利用属性自表达的表示方式，考虑到了全体不同属性之间的相互关系；而PCA算法仅做了高维到低维的投影，RFS算法未考虑数据之间的关系，LPP算法只考虑了数据局部的关系。而SR_FS算法又结合了稀疏学习，弥补了单一方法的不足，因此能有效地选择主要的类判别属性和去除噪音属性，显著提高分类性能。根据图1-图6可以直观地看出，SR_FS算法在各数据集上10次运行的结果的折线大部分能在其他算法的上方，表明SR_FS算法表现出了更好的效果。

分析表2的方差统计结果可看出，SR_FS算法在各个数据集的10次运行结果取得的方差与各对比算法相比，均能取得最小的方差。分析表3的变异系数统计结果可看出，SR_FS算法在各数据集上得到的变异系数均为最小。通过各算法10次运行结果得到的方差(表2)和变异系数(表3)的比较可知，在多个不同数据集上，经本文SR_FS算法属性选择后的数据，均能达到更加准确和稳定的分类效果。因此，本文SR_FS算法比对比算法有更好的鲁棒性。

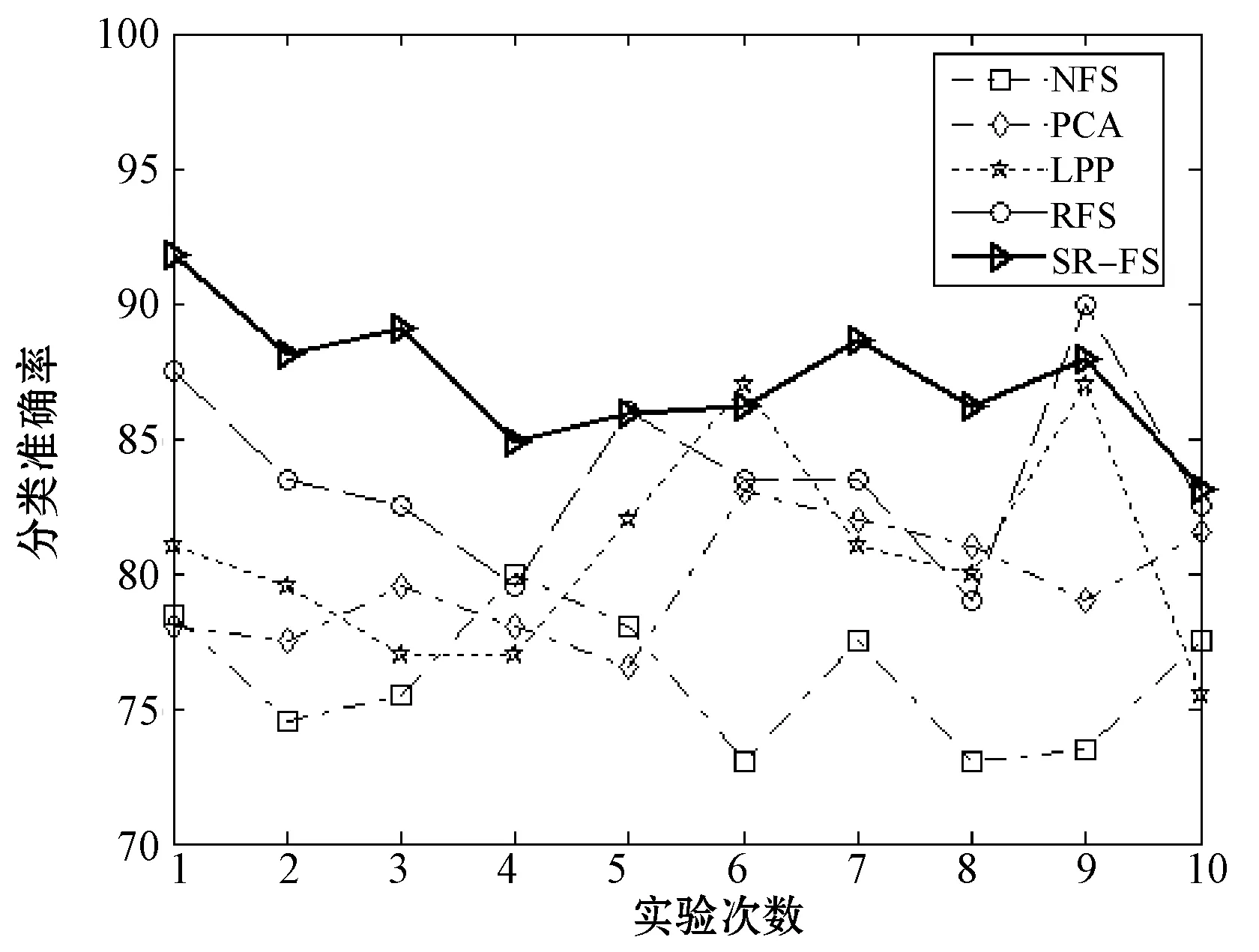
图1 数据集madelon上各算法准确率对比

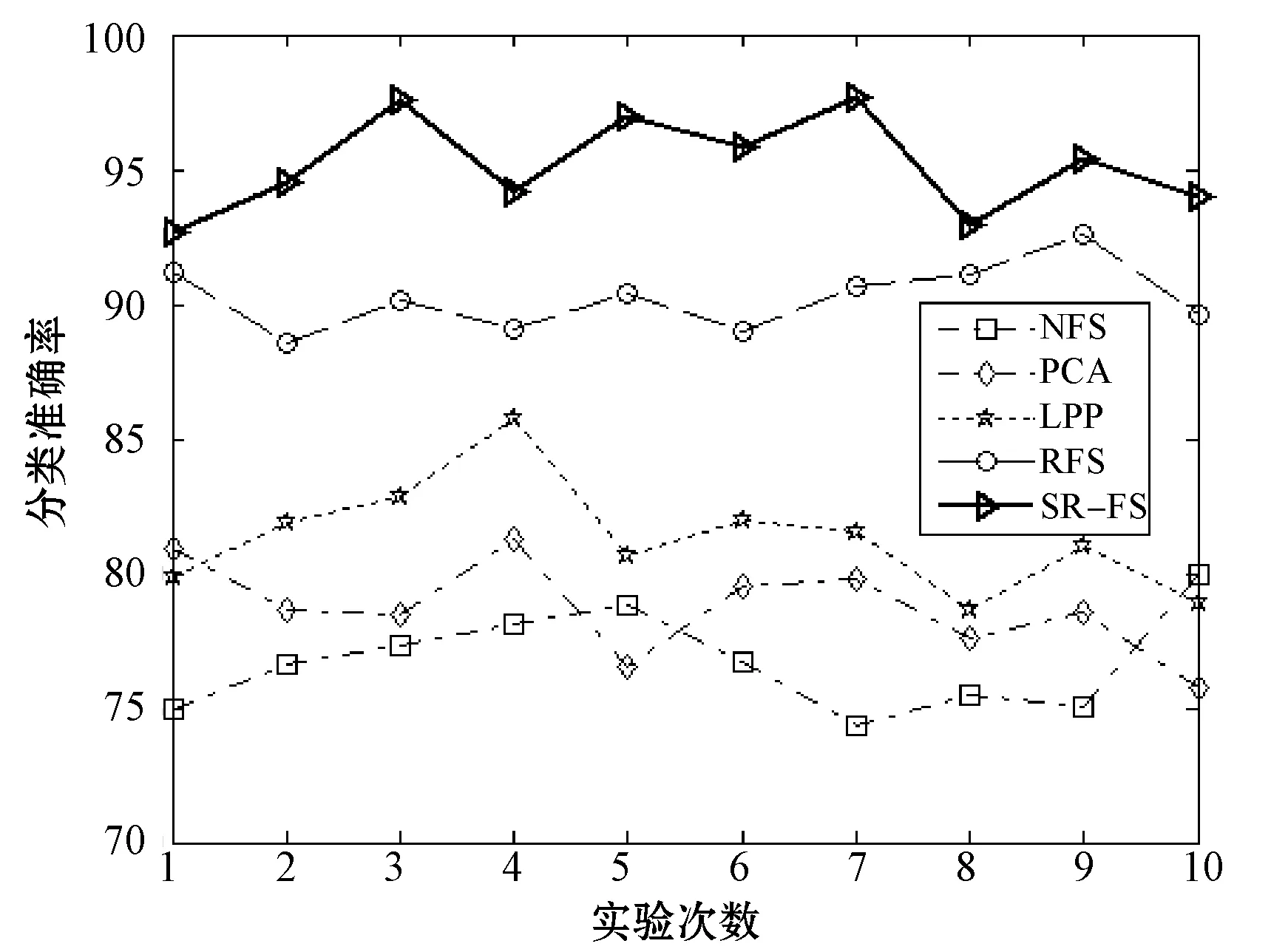
图2 数据集mask上各算法准确率对比

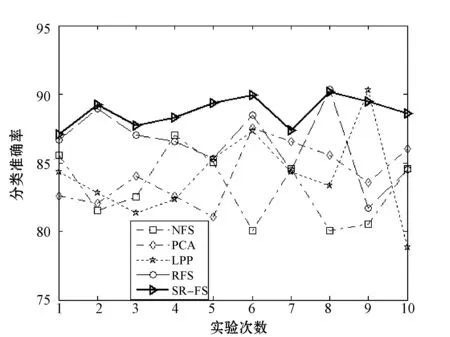
图3 数据集train上各算法准确率对比

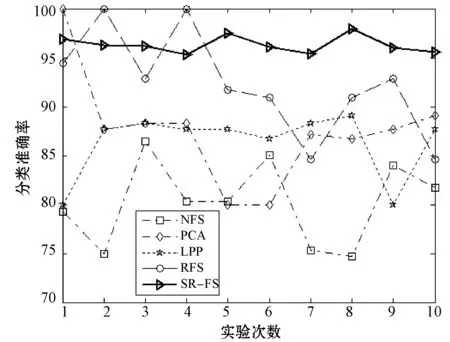
图4 数据集warpAR10P上各算法准确率对比

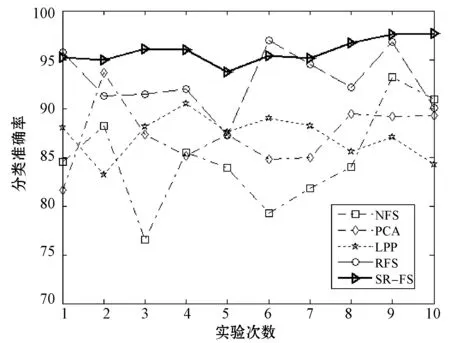
图5 数据集TOX-171上各算法准确率对比

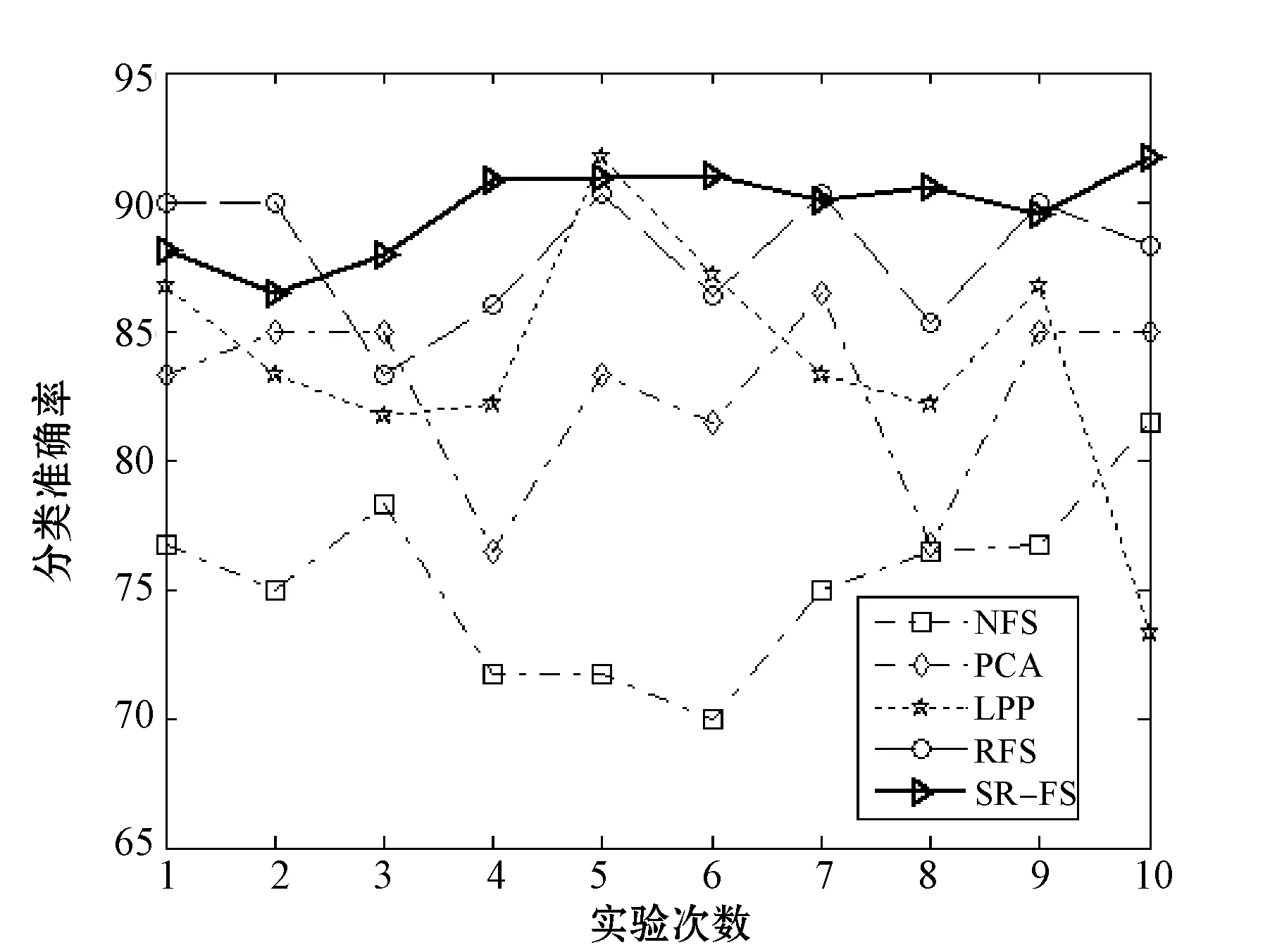
图6 数据集DBworld上各算法准确率对比

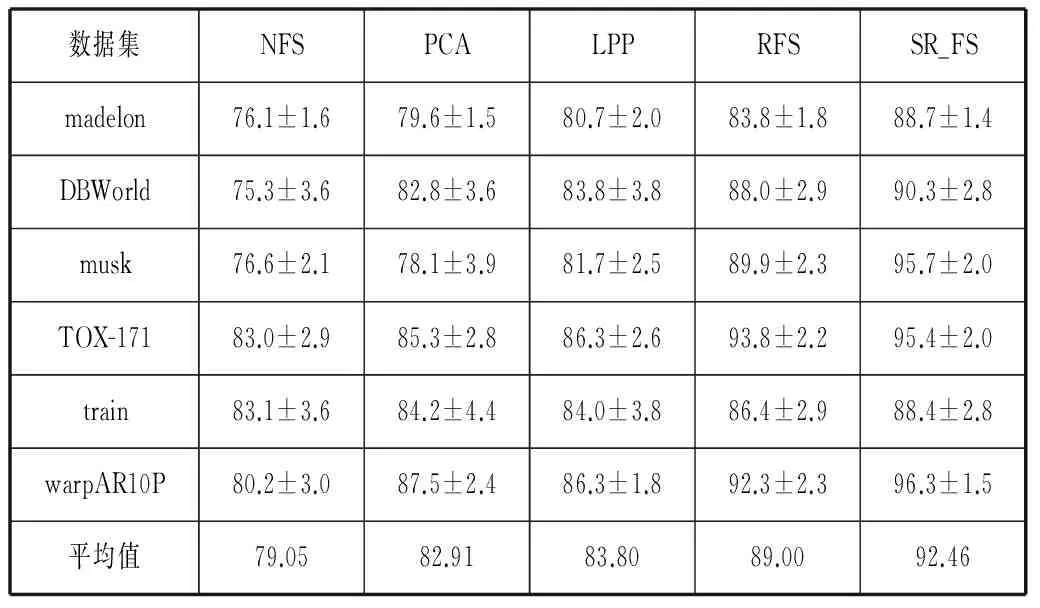
表2 准确率的均值统计结果(百分比%)

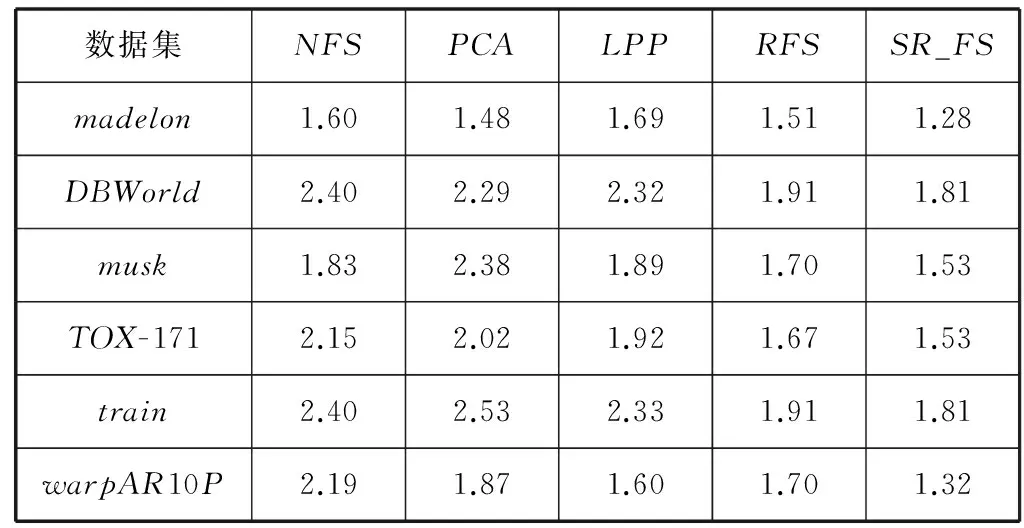
表3 各数据集十次结果的变异系数统计结果(百分比%)

5 结 语

本文提出一种新的属性选择算法SR_FS算法，即通过使用数据本身的性质来构建自表达系数矩阵，并整合L2,1-范数作为稀疏正则化项，来达到选择重要属性的目的。该算法有效地利用属性的特性来构造自表达系数矩阵并和稀疏属性选择有机融合在一起，达到了进行自动属性选择的目的。其既扩展了属性自表达的理论应用范畴，也弥补了稀疏学习在属性选择处理方面的不足。经实验表明，本文算法能够在分类准确率和稳定性上取得显著提高。在后续的工作中，将尝试在半监督属性选择方面拓展验证本文提出的算法，并尝试使用更先进的技术改进。

[1] Zhu X F,Suk H I,Shen D G.Matrix-Similarity Based Loss Function and Feature Selection for Alzheimer’s Disease Diagnosis[C]//Computer Vision and Pattern Recognition (CVPR),2014 IEEE Conference on.IEEE,2014:3089-3096.

[2] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[3] Zhao Z,Wang L,Liu H.Efficient spectral feature selection with minimum redundancy [C]//Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence,Atlanta,2010:673-678.

[4] Li Z C,Yang Y,Liu J,et al.Unsupervised feature selection using nonnegative spectral analysis [C]//Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence,Toronto,2012:1026-1032.

[5] Zhu X F,Huang Z,Yang Y,et al.Self-taught dimensionality reduction on the high-dimension-al small-sized data[J].Pattern Recognition,2013,46(1): 215-229.

[6] Yang Y,Shen H T,Ma Z G,et al.L2,1-norm regularized discriminative feature selection for unsupervised learning [C]//Proceedings of the Twenty-Second international joint conference on Artificial Intelligence,2011，2:1589-1594.

[7] Wan J W,Yang M,Chen Y J.Discriminative cost sensitive Laplacian score for face recognition[J].Neurocomputing,2015,152:333-344.

[8] Zhu X F,Huang Z,Yang Y,et al.Self-taught dimensionality reduction on the high-dimensional small-sized data[J].Pattern Recognition,2013,46(1):215-229.

[9] Nie F P,Huang H,Cai X,et al.Efficient and Robust Feature Selection via Joint L2,1-Norms Minimization[C]//Advances in Neural Information Processing Systems,2010:1813-1821.

[10] Yao L,Zhang X J,Li D H,et al.An interior point method for L1/2-SVM and application to feature selection in classification[J].Journal of Applied Mathematics,2014(1):1-16.

[11] Zhu P F,Zuo W M,Zhang L,et al.Unsupervised feature selection by regularized self-representation[J].Pattern Recognition,2015,48(2):438-446.

[12] Zhu X F,Huang Z,Shen H T,et al.Linear cross-modal hashing for efficient multimedia search[C]//MM 2013-Proceedings of the 2013 ACM International Conference on Multimedia， 2013:143-152.

[13] Zhao Z,Wang L,Liu H,et al.On Similarity Preserving Feature Selection[J].IEEE Transactions on Knowledge and Data Engineering,2013,25(3):619-632.

[14] Mitra P,Murthy C A,Pal S K.Unsupervised feature selection using feature similarity[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(3):301-312.

[15] Nie F P,Xiang S M,Jia Y Q,et al.Trace ratio criterion for feature selection[C]//AAAI’08,2008,2:671-676.

[16] Feature selection datasets[EB/OL].[2015-04-10].http://featureselection.asu.edu/datasets.php.

[17] LIBSVM—A Library for Support Vector Machines.[EB/OL].[2015-04-10]. http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[18] Yang Y,Shen H T,Ma Z G,et al.l2,1-norm regularized discriminative feature selection for unsupervised learning[C]//Proceedings of the Twenty-Second international joint conference on Artificial Intelligence.AAAI Press,2011,2:1589-1594.

[19] Zhu X F,Zhang L,Huang Z.A sparse embedding and least variance encoding approach to hashing[J].IEEE Transactions on image processing,2014,23(9):3737-3750.

FEATURE SELECTION ALGORITHM WITH ROBUST SELF-REPRESENTATION BASED ON SPARSE LEARNING

He Wei1Liu Xingyi2*Cheng Debo1Hu Rongyao1

1(GuangxiKeyLabofMulti-sourceInformationMiningandSecurity,GuangxiNormalUniversity,Guilin541004,Guangxi，China)2(QinzhouUniversity,Qinzhou535000,Guangxi，China)

Inspired by the high efficiency of feature selection in dealing with high-dimensional data and the success application of low-rank self-representation in subspace clustering,we proposed a sparse learning-based self-represented feature selection algorithm.The algorithm first represents every feature in other feature linearity to obtain the self-representation coefficient matrix; then in combination with sparse learning theory (i.e.to integrate the L2,1-norm as a sparse regularisation punishment object function) it implements feature selection.With the evaluation indexes of classification accuracy and variance,and compared with the algorithms to be contrasted,experimental results indicated that the proposed algorithm could be more efficient in selecting important features and showed excellent robustness as well.

High-dimensional data Feature selection Featrue self-representation Sparse learning

2015-07-27。国家自然科学基金项目(61170131，61263035，61363009)；国家高技术研究发展计划项目(2012AA011005)；国家重点基础研究发展计划项目(2013CB329404)；广西自然科学基金项目(2012GXNSFGA060004)；广西高校科学技术研究重点项目(2013 ZD041)；广西研究生教育创新计划项目(YCSZ2015095，YCSZ2015096)。何威，硕士，主研领域：数据挖掘，机器学习。刘星毅，硕士。程德波，硕士。胡荣耀，硕士。

TP181

A

10.3969/j.issn.1000-386x.2016.11.045