基于改进自适应小波基的织物疵点检测算法

刘洲峰 李 阳 李春雷

(中原工学院电子信息学院 河南 郑州 450007)



基于改进自适应小波基的织物疵点检测算法

刘洲峰 李 阳 李春雷

(中原工学院电子信息学院 河南 郑州 450007)

为了改进基于自适应小波的织物疵点检测效果，提出一种基于改进自适应小波基的织物疵点检测算法。首先通过不同限定条件优化得到多个自适应小波基；然后分别对疵点图像进行小波分解，采用最大类间方差法分割子图像；最后将多种自适应小波基分割后的图像进行融合得到检测结果。实验结果证明，该算法能够在较好保留疵点信息的同时，有效地减少检测结果中的噪声点。

自适应小波 小波分解 图像融合 疵点检测

0 引 言

在织物生产过程中，织物疵点的自动检测是保证质量的重要环节。基于机器视觉的疵点检测方法不同于传统的人眼检测，具有检测速度高、漏检、错检率低等优点，被国内外学者广泛研究[1]。

现有织物疵点检测方法主要分为三大类：统计法、模型法和谱分析法[1]。其中统计法较为适合检测特定类别的疵点；模型法取决于对背景纹理的建模，运算量较大；谱分析法通过将图像变换至变换域，能够更好地突出并检测疵点。在谱分析法中，小波变换有良好的多分辨能力和空间定位特性，相比傅里叶变换与Gabor变换能够自适应空间和频率的局部变换。基于传统小波基的织物疵点检测算法[2-4]无法满足多种纹理不同织物的检测。基于自适应小波基的织物疵点检测算法[5-7]可以根据不同织物的纹理背景优选出合适的小波基，能够较好地检测出不同纹理背景的织物疵点。由于图像自身可能包含噪声[8]，且经小波分解后直接用于疵点检测的子图像经过了高通滤波，处理后所得二值图像容易出现很多噪声点，从而影响检测结果。

相比已有的基于单限定条件自适应小波基的检测算法，本文所采用的构造多种不同自适应小波基分别对疵点图像分解再进行融合的检测算法，能够在有效检测出疵点信息的同时，减少噪声点的出现。

1 图像小波静态分解

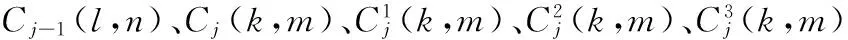
图1 小波分解算法示意图

小波分解算法如下：

(1)

小波静态分解[9]是在小波分解算法中除去其中所有的二抽取，使子图像的大小约为分解前图像大小。小波的静态分解能够较完整保留疵点信息，准确定位疵点。因此，在对图像分解时，选用小波静态分解。

2 自适应小波基的构造

2.1 构造小波基滤波器库

构造织物疵点检测所需的自适应小波基，就是从满足正交条件的一定长度的小波滤波器库中，优选出适合待检测织物图像的滤波器系数。正交低通滤波器系数记作hk，正交高通滤波器系数记作gk，hk和gk满足关系式：

式中H(ω)和G(ω)满足正交镜像关系。选定滤波器长度，通过给定不同初值可以得到多组满足以上各式的解，将其作为滤波器库，供优选小波基使用。

2.2 优选自适应小波基

优选自适应小波基，是指通过某一限定条件从滤波器库中优选出适合目标纹理图像的滤波器。本文将几种常用的织物纹理特征的表征形式[10]作为限定条件，通过对正常织物图像进行处理，通过对比结果，优选出较好的滤波器。

(1) 子能量

正常织物图像小波分解后，将得到图像的高通子能量最小作为限定条件，能够使小波基系数将纹理特征体现出来，提高对织物疵点的敏感性。限定条件式表示如下：

(9)

(10)

式中Eh和Ev分别为纬向和经向子图像的最小能量，HL(x,y)和LH(x,y)分别为小波静态分解纬向和经向子图像的灰度值，(x,y)∈f表示子图像上的所有像素点。

(2) 极差

将子图像的灰度极差最小，即图像静态分解后得到的小波系数最大值和最小值的差值最小作为限定条件，能够缩小子图像的小波系数分布范围，使小波基系数与文理特征更加匹配。限定条件式表示如下：

(11)

(12)

式中EP和Eq分别为纬向和经向子图像的最小极差。

(3) 纹理波动

将子图像每一行或每一列灰度值的和之间波动最大作为限定条件，能够使小波基与织物纹理联系更紧密，使小波基自身就能一定程度上反映纹理特征。限定条件式表示如下：

(13)

(14)

式中Em和En分别为纬向和经向最大波动。

3 疵点检测

通过不同的限定条件优选出多个小波基后，分别对织物疵点图像进行二层小波静态分解。由于织物图像的纹理信息主要集中在纬向和经向子图像中[4]，利用阈值分割法对得到的纬向子图像HL(xn,yn)和经向子图像LH(xn,yn)进行分割(其中n为限定条件的数目)；再将分割后的图像进行融合，得到最终的检测结果。

3.1 基于最大类间方差法的阈值分割

最大类间方差法，又称Otsu算法，是在灰度直方图的基础上，通过最小二乘法推导出来，具有统计意义上的最佳分割。Otsu算法以最佳阈值将图像的灰度值分割成两部分，使两部分之间的方差最大，具有最大的分离性。

记k为目标与背景的分割阈值，取值范围为0～255，目标和背景所对应的像素数占图像总像素数的比例为WA和WB，对应的平均灰度分别为μA和μB，图像的总平均灰度为μ，则类间方差σ2和使类间方差取最大值的最佳分割阈值k的计算公式如下：

σ2(k)=WA(μA-μ)2+WB(μB-μ)2

(15)

k=argmax(σ2(k))

(16)

利用最佳阈值k将目标图像二值化，二值化结果C(xn,yn)如下：

(17)

3.2 多图像融合

由于织物图像采集时光照不匀、织物自身复杂的纹理、小波分解中的高通滤波等因素，子图像经过阈值分割后往往会产生较多噪声点。用形态学滤波方法可以一定程度上滤除噪声，但同时会影响到疵点部分的检测结果。如图2所示，(a)为破洞的疵点图像，(b)、(c)、(d)为小波二层分解后子图像不同程度去噪的阈值分割结果。可以看出，在滤除噪声点的同时，疵点的检测结果也会受到影响。

图2 疵点图像与不同程度去噪的结果

为了在滤除阈值分割后图像噪声点的同时，尽可能好地保留疵点部分，本文提出一种多图像融合算法。采用三种不同限定条件(n=1,2,3)优化得到的自适应小波对疵点图像分别进行二层小波分解。将分解后纬向子图像HL(xn,yn)或经向子图像LH(xn,yn)经阈值分割以及形态学滤波处理后得到的结果CHL(xn,yn)和CLH(xn,yn)进行融合，得到最终的检测结果RHL和RLH。融合表达式如下：

RHL=CHL(x1,y1)&CHL(x2,y2)+

CHL(x1,y1)&CHL(x3,y3)+

CHL(x2,y2)&CHL(x3,y3)

(18)

RLH=CLH(x1,y1)&CLH(x2,y2)+

CLH(x1,y1)&CLH(x3,y3)+

CLH(x2,y2)&CLH(x3,y3)

(19)

式(18)、式(19)表示当CHL(xn,yn)和CLH(xn,yn)中某一像素点两次或两次以上为1时，在最终得到的结果R中该点为1；否则为0。

4 实验结果及分析

选取四幅斜纹胚布织物图像，如图3所示，疵点种类分别为破洞、断经、断纬和坏地，像素为512×512。取滤波器长度为8，滤波器容量为100，由正常织物图像和三种限定条件优选出自适应小波基滤波器系数。表1列出了三种限定条件下优选得到的自适应小波基滤波器系数。

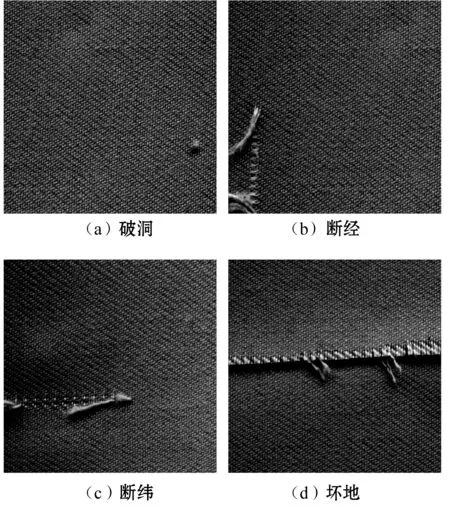
图3 织物疵点图像

子能量极差纹理波动纬向匹配0.3915-0.1937-0.1991-0.06090.41570.0225滤波器系数-0.02890.05130.54810.3645-0.0109-0.3691-0.05240.04750.5070-0.08350.32430.64840.39680.8020-0.14890.4870-0.02190.4054经向匹配0.3511-0.1462-0.1991-0.06090.4085-0.1431滤波器系数0.0093-0.00030.54810.36450.01280.0011-0.0087-0.00010.5070-0.0835-0.0122-0.00150.35540.8537-0.14890.48700.29800.8506

本文选择采用纬向匹配滤波器系数对疵点图像进行二层小波分解。通过最大类间方差法获得最佳阈值，子图像经过阈值分割和形态学滤波处理后得到结果。三种不同限定条件下处理结果如图4-图6所示。分别将各个疵点图像的三种检测结果以式(18)进行融合，得到融合结果如图7所示。

图4 极差最小限定条件下检测结果

图5 子能量最小限定条件下检测结果

图6 纹理波动限定条件下检测结果

图7 多图像融合结果

比较图7和图4-图6中结果，融合后的检测结果较完整地保留了疵点信息，同时有效地减少了融合前图像中的噪声点。可以看出，本文提出算法具有良好的疵点分割和定位结果，能够有效地实现疵点检测。

这里需要说明，如果三种限定条件的目标滤波器库相同，有可能优选出相同的小波基。由于满足两种或三种限定条件，此小波基适应性强，同时融合结果与部分融合前图像相同。

5 结 语

本文提出一种基于改进自适应小波基的织物疵点检测算法，利用多种限定条件优选出不同的小波基，将多种基于自适应小波基的疵点检测图像进行融合得到检测结果。由于噪声点较小，随机性强，出现的概率低，疵点部分面积较大，结果中出现的概率较高。与融合前单限定条件优选的小波基检测算法相比，基于自适应小波基的多图像融合疵点检测算法能够在较完整保留疵点信息的同时减少噪声点，有效实现疵点检测。

[1] 李文羽,程隆棣.基于机器视觉和图像处理的织物疵点检测研究新进展[J].纺织学报,2014,35(3):158-164.

[2] Fernández J A,Orjuela S A,lvarez J,et al.Fabric defect detection using the wavelet transform in an ARM processor[C]//Proceedings of SPIE-The International Society for Optical Engineering,2012,8300:617-636.

[3] Han Y F,Shi P F.An adaptive level-selecting wavelet transform for texture defect detection[J].Image and Vision Computing,2007,25(8):1239-1248.

[4] Ghazvini M,Monadjemi S A,Movahhedinia N,et al.Defect Detection of Tiles Using 2D-Wavelet Transform and Statistical Features[C]//Proceedings of World Academy of Science,Engineering & Technology,2009,49:901-904.

[5] 石佶.基于小波分析和阈值分割的织物疵点检测[D].苏州:苏州大学,2013.

[6] 魏炜.基于自适应双正交小波的织物疵点边缘检测[J].西安工程大学学报,2013,27(3):369-374.

[7] 单亦杰,韩润萍.基于二层自适应正交小波的疵点检测[J].微计算机信息,2007,23(9):303-304,274.

[8] 郑春兰,张凤生,时洪光.基于 LabVIEW 的织物疵点检测的小波去噪方法研究[J].现代仪器,2009 (6):46-48.

[9] 管声启,石秀华,王筠.基于小波静态分解的离散小疵点检测[J].天津工业大学学报,2010,29(5):73-76.

[10] 牛存才,汪军,张孝南,等.基于遗传规划的织物自适应正交小波基的构造和优化[J].纺织学报,2012,33(9):40-46.

FABRIC DEFECT DETECTION ALGORITHM BASED ON IMPROVED ADAPTIVE WAVELET BASIS

Liu Zhoufeng Li Yang Li Chunlei

(SchoolofElectricandInformationEngineer,ZhongyuanUniversityofTechnology，Zhengzhou450007，Henan,China)

In order to improve the effect of adaptive wavelet-based fabric defects detection,we proposed a fabric defect detection algorithm which is based on the improved adaptive wavelet basis.First,the algorithm obtains a number of self-adaptive wavelet basis by optimisation with different limited conditions;then these self-adaptive wavelets are used to make wavelet decomposition on defect images respectively,and the Otsu method is used to segment the sub-image;finally,it fuses the images segmented by multiple adaptive wavelet basis to get the detection result.Experimental results demonstrate that the proposed algorithm can effectively reduce the noise points in test result while well preserving the defect information.

Self-adaptive wavelet Wavelet decomposition Image fusion Defect detection

2015-04-02。国家自然科学基金项目(61379113);河南省基础与前沿技术研究项目(142300410042)；郑州市科技领军人才项目(131PLJRC643)。刘洲峰，教授，主研领域：图像处理与模式识别。李阳，硕士，李春雷，博士。

TP3 391.9

A

10.3969/j.issn.1000-386x.2016.11.034